Методика генерации данных и получения единого массива технологических параметров на основе ретроспективной информации

В условиях сложных многоступенчатых процессов фиксируются и обрабатываются значительные объемы технологической информации.

Однако отсутствие единой системы слежения за производимой продукцией часто вызывает сбои в формировании массивов технологической информации. Кроме того, во многих случаях появляется возможность собрать лишь ограниченные наборы данных о технологии и свойствах готовой продукции. В этих условиях встает задача генерации массивов технологических факторов, достаточных для статистической обработки, и соединения локальных массивов в единый массив без потери информативности.

Одномерная генерация технологических факторов

На основе ретроспективной информации можно определить закон распределения основных технологических величин и представить их в виде гистограммы.

Пусть диапазон изменения разбит на K = 6 равных участков. Частота попадания в каждый из участков: b^VK^ .

к

^bj = N,                 (1)

i = 1

где N – объем выборки [2]. Для генерации новой выборки по данному закону можно использовать генератор случайной величины, подчиняющийся равномерному закону.

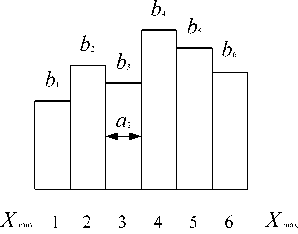
Рис. 1. Гистограмма технологической величины

Диапазон генерации (от 0 до объема исходной выборки N ) разбивается на K участков (то есть число участков соответствует числу столбцов исходной гистограммы). Причем длина участка равна частоте попадания опытов в соответствующий столбец гистограммы.

генерируемая точка

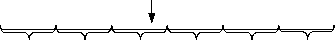
0                              N b, b b, b4 b5 Ы

Рис. 2. Генерация значений по заданной гистограмме

При генерации одной точки ее значение b попадает в bj участок. Таким образом, чем выше вероятность попадания в участок гистограммы, тем шире длина соответствующего участка при генерации. Генерируемое значение можно определить по формуле

+ £a/+xmin, (2)

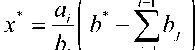
где a, = const – интервал исходной гистограммы, i – номер участка, в который попала генерируемая величина.

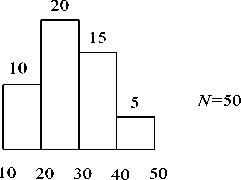
Рис. 3. Пример исходной гистограммы

Рассмотрим пример генерации для гистограммы, изображенной на рис. 3. Формируем ряд для гистограммы (см. рис 4).

b,               b.

O 10           30       45 50

Рис. 4. Ряд генерации для заданной гистограммы

Генерируем величину bx с помощью равномерного генератора от 0 до 50. Пусть b, = 20, = 10. Полученное значение соответствует второму интервалу гистограммы ( i = 2). По (2) определяем реальное значение генерируемого фактора :

i = ^(20-10)+10 + 10 = 5 + 20 = 25.

Пусть b*, = 35 . В итоге определяем следующее значение x* = *1(35-30) +30 = 33,3-нерации представлена на рис. 5.

Схема ге-

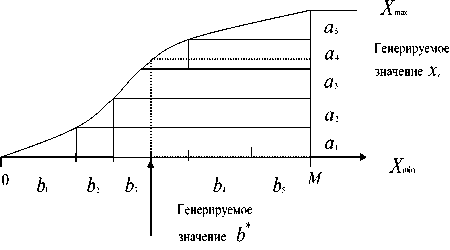
Рис. 5. Схема генерации факторов

Генерация многомерных массивов

Для многомерных законов можно использовать аналогичный подход [3]. Пусть X – факторы технологии X = (x₁,...,x„), Y – показатели качества У=(У1,...,^). В результате проведения N опытов получено N единиц продукции качества Y . Каждый фактор технологии колеблется в определенных границах: Xj < Xj < Xj . Диапазон разбивается на K участков, равных по величине, число которых следует выбирать с учетом требований и ограничений технологий. В каждом конкретном опыте значения фактора ^Xl будут попадать в од ин из выделенных участков: X - , где k = l,K . Информация для всех таких ситуаций при частоте возникновения ситуации n_s > 0 заносится в таб лиц у 1. Для каждого x. указывается число k = X,K .

Таблица 1. Частота возникновения технологических ситуаций

№	Технологическая ситуация	Сочетание факторов х^ : х*, х^	Частота возникновения ситуации
1	То)	11111	35
2	ТЖ)	11112	13
D	KXSX	ккккк	44

Чтобы не загромождать таблицу и не указывать значения диапазонов для Xj , при кодировки конкретной технологической ситуации в таблице для каждого X- указывается цифра k = l,K . Полученная таблица представляет собой M -мерную гистограмму. Следовательно, необходимо получить данную таблицу из входных данных.

Рассмотрим пример таблицы для M = 2 и K = 3 (см. таблицу 2). Если все частоты возникновения ситуаций расположить одну за другой вдоль одной линии (см. рис. 6), то получаем линию, разделенную на интервалы различной длины. Каждому интервалу соответствуют свои диапазоны входных параметров. Таким образом, сгенерировав число от 0 до N по равномерному закону распределения, можно определить, в какой интервал попало значение, а затем для каждого фактора случайным образом выбрать значение из соответствующего интервала.

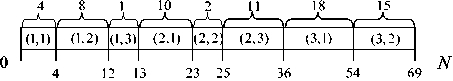
Рис. 6. Разложение двумерной гистограммы в ряд

Таблица 2. Пример таблицы для M = 2 и K = 3

№	Сочетание факторов к к        к к .хх,...,хп	Частота возникновения ситуации ns	Результат генерации
1	(1,1)	4	7
2	(1,2)	8	11
3	(1,3)	1	2
4	(2,1)	10	15
5	(2,2)	2	0
6	(2,3)	11	13
7	(3,1)	18	30
8	(3,2)	15	22

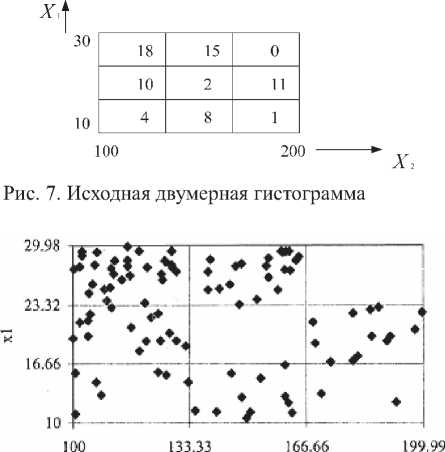
В качестве примера можно рассмотреть двумерную гистограмму (см. рис. 7). По данной ги- стограмме было сгенерировано 100 значений, и результат представлен в таблице 2 и на рис. 8.

X?

Рис. 8. Распределение сгенерированных значений в двумерном пространстве

Из гистограммы видно, что генерация происходит по заданному закону.

Исправление грубых погрешностей в массиве

В исследуемых массивах данных могут встречаться грубые погрешности или отсутствовать некоторые значения. Самый простой способ заключается в исключении всей строки данных при наличии таких нарушений. Однако это ведет к сокращению объема выборки. Ошибочные данные можно заменить сгенерированным значением. В этом случае выбирается строка, в которой присутствует грубая погрешность. По достоверным данным строится совместный закон распределения и выбирается сочетание факторов, которому соответствует данная строка (см. таблицу 1). Для данного сочетания определяется закон распределения исправляемой величины. Затем осуществляется описанная выше методика генерации.

Пусть строка данных содержит 3 фактора, один из которых отсутствует или аномален. Первые два фактора относятся к одному из сочетаний, например, 11х, где х – аномальное значение фактора. Для генерации определяются вероятности попадания в один из выбранных участков генерируемого фактора. Для рассмотренного случая (выделен в таблице 3) это числа (5; 7; 10), которые и являются основой для получения нового значения, вносимого в массив. Если бы сочетание факторов было, например, 12х, то для генерации были бы выбраны числа (4; 6; 8).

Таблица 3. Пример таблицы частот возникновения технологических ситуаций

№	Сочетание факторов к к к xt х2 х3			Частота появления сочетания факторов
1	1	1	1	5
2	1	1	2	7
3	1	1	3	10
4	1	2	1	4
5	1	2	2	6
6	1	2	3	8
D	3	3	3	11

Соединение массивов в сквозной массив

Если существуют два и более массивов технологических факторов, взаимосвязь между которыми не определена явно, но вытекает из одних и тех же режимов обработки каждой единицы продукции, то при наличии пересекающихся факторов (факторы, принадлежащие как одному, так и другому массиву) можно определить примерное продолжение цепочки из первого массива во вто- ром. Метод слияния массивов работает следующим образом.

Рассмотрим два массива, имеющие одинаковые (пересекающиеся) факторы (см. рис. 9). В каждом из массивов для всех факторов находятся минимальные и максимальные значения. Для пересекающихся параметров определяется общее минимальное и максимальное значение, являющееся глобальным минимумом или максимумом двух массивов. В обоих массивах каждый из факторов разбивается на определенное количество интервалов, равных по величине, причем каждый из пересекающихся параметров должен дробиться на одинаковое число частей и в первом, и во втором массивах. Рассчитывается частота возникновения каждой комбинации пересекающихся факторов в исследуемых массивах и строится М-мерная гистограмма, аналогичная таблице 2.

Для этих комбинаций рассчитываются соответствующие комбинации непересекающихся факторов для каждого массива. Производится выбор сочетаний пересекающихся факторов (аналогично методу генерации) и соответствующих им непересекающихся. Затем формируется новый массив, содержащий полный набор технологических факторов.

Методика формирования сквозного массива данных представлена на рисунке 9.

Пусть первый массив содержит факторы х ₁, х ₃, х ₄, х ₅, х ₆, х ₇, х ₁₀, а второй – х ₁, х ₂, х ₃, х ₄, х ₇, х ₈, х ₉, х ₁₀. Одинаковыми (пересекающими) факторами являются х ₁, х ₃, х ₄, х ₇, х ₁₀. Каждый фактор обоих

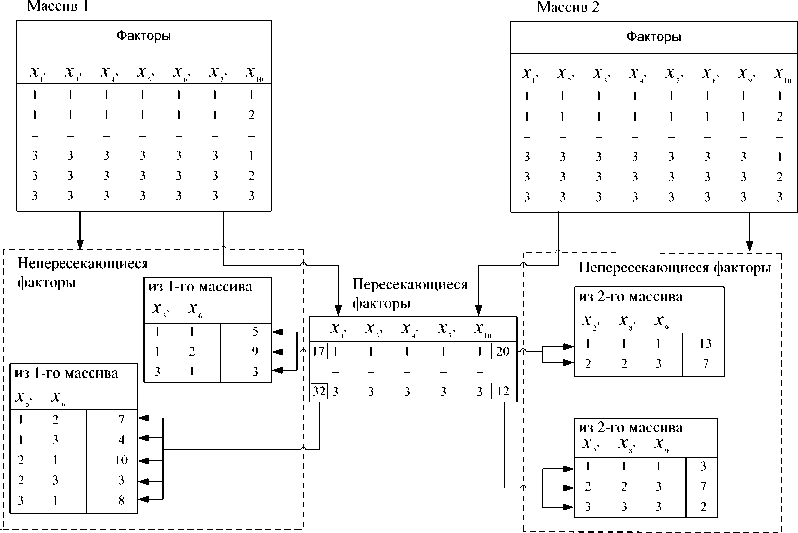
Рис. 9. Методика формирования сквозного массива данных

массивов разбивается на три участка, и формируются совместные законы распределения. Для пересекающихся факторов также формируется совместный закон распределения (CЗР) и определяются все ненулевые (реально встречающиеся) сочетания факторов. Процедура соединения массивов осуществляется последовательно для всех строк первого и второго массивов. Взяв строку одного из массивов, определяют участок СЗР (вариант сочетания факторов), которому она соответствует. Например, на рис. 9. сочетание (1 1 1 1 1). В первом массиве такое сочетание встречалось 17 раз, во втором 20. Для данного сочетания формируется CЗР непересекающихся факторов 1-го массива ( х ₅, х ₆), представленный на рисунке (значения 5; 9; 3), и по описанной выше методике генерируются значения х ₅, х ₆. Аналогично для непересекающихся факторов второго массива ( х ₂, х ₅, х ₉) генерируются значения.

Однако совместный закон распределения всех непересекающихся факторов ( х ₂, х ₅, х ₆, х ₈, х ₉) может не соответствовать реальному закону. Например, по 1 фактору для каждого массива. Пусть каждый разбивается на 2 участка и число попаданий в каждый равно 100. На рис. 10 представлены варианты СЗР.

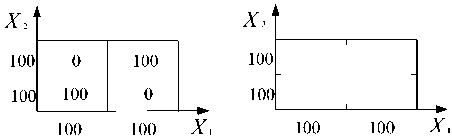
Рис. 10. Варианты совместных законов распределения двух факторов

50	50
50	50

Чтобы избежать подобных ошибок при генерации, необходимо использовать обучающую выборку или регрессионные модели зависимости непересекающихся факторов. По обучающей выборке, сгенерировав факторы одного из массивов, определяем факторы другого массива, используя общий СЗР.

Если использовать регрессионные модели, то по сгенерированным факторам одного массива прогнозируется значение другого, определяются сочетания факторов, которым прогнозируемые значения соответствуют, и внутри полученных участков генерируются случайным образом в новые значения [1]. Для проверки работоспособности функции слияния массивов проведем тестовое слияние. Статистические характеристики факторов первого и второго, исходных и сгенерированных, массивов представлены в таблице 4 [3].

Таблица 4. Статистические характеристики факторов

Объем	358	509	2000
Параметры	Первый массив	Второй массив	Сгенерированный массив
Предел текучести q , МПа
Минимум	165	170	169,350
Максимум	230	250	249,8
Среднее	185,615	194,145	197,644
Дисперсия	289,985	2843,82	1495,08
Предел прочности ов , МПа
Минимум	240	240	241,032
Максимум	380	390	379,952
Среднее	317,877	331,788	329,846
Дисперсия	508,342	1744,54	1662,51
Относительное удлинение 5, %
Минимум	32	33	33,002
Максимум	48	49	47,9928
Среднее	42,324	40,4499	41,5767
Дисперсия	10,5263	25,6935	25,6835
Твердость HRB
Минимум	32	32	32.121
Максимум	52	58	51,9948
Среднее	36,2067	37,8134	36,9507
Дисперсия	33,5383	58,423	53,541
Глубина лунки по Эриксену J ,мм
Минимум	10,7	10,9	10,973
Максимум	14.0	13.7	13,962
Среднее	10,665	11,0334	11,4447
Дисперсия	0,369	0,372	0,359

Анализ таблицы 4 показывает, что статистические параметры факторов выходного массива сохраняются по отношению к статистическим характеристикам факторов исходных массивов.

Приведем данные корреляционного анализа. Матрицы корреляций факторов первого и второго исходных и сгенерированного массивов представлены в таблице 5. Здесь первая строка – первый массив; вторая строка – второй массив; третья строка – сгенерированный общий массив.

Таблица 5. Корреляционные матрицы пересекающихся факторов

Факторы	(Т^ , МПа	сгг, МПа	5, %	HRB	Е ’ ММ
	1,0000	0,7344	0,2545	0,4723	-0,0539
	1,0000	0,8636	0,3614	0,2723	0,3118
МПа	1,0000	0,3578	0,3459	0,1675	0,1728
	0,7344	1,0000	0,4341	0,2841	0,3019
	0,8636	1,0000	0,6554	0,3306	0,3847
МПа	0,3578	1,0000	0,5421	0,1938	0,3245
	0,2545	0,4341	1,0000	0,4241	0,0179
5, %	0,3614	0,6554	1,0000	0,2712	0,3023
	0,3459	0,5421	1,0000	0,2207	0,2854
	0,4723	0,2841	0,4241	1,0000	-0,2832
HRB	0,2723	0,3306	0,2712	1,0000	0,0629
	0,1675	0,1938	0,2207	1,0000	-0,0058
	-0,0539	0,3019	0,0179	-0,2832	1,0000
J в ’	0,3118	0,3847	0,3023	0,0629	1,0000
мм	0,1728	0,3245	0,2854	-0,0058	1,0000

Заключение

Полученные результаты подтверждают возможность использования данного подхода для генерации массивов и возможности их слияния в единый массив.