Методика идентификации производственных характеристик на основе кластеризации данных

Основной задачей, стоящей в настоящее время перед промышленными предприятиями, является повышение энергетической эффективности производства. Одним из подходов решения поставленной задачи является выявление резервов повышения эффективности производственных систем на основе идентификации производственных характеристик их элементов по данным эксплуатации.

Реальные производственные характеристики, как правило, зависят от множества внутренних режимных факторов, поэтому не представляется возможным учесть все множество режимных факторов вследствие их большого многообразия для различных составляющих технологических процессов. Предлагается использовать в качестве производственных характеристик элементов сетей не только среднестатистические характеристики, но и мажорантные и минорантные, которые в совокупности описывают рабочую область производственных характеристик. В дальнейшем мажорантные и минорантные характеристики будем называть граничными.

В качестве примера на рис. 1 представлена паровая характеристика турбины электрической станции. Паровая характеристика состоит из базовой зависимости потребления пара (£>0) от выработанной электрической мощности^) и тепловой мощности (0Т). Реальная диаграмма отличается от базовой на величину поправок по внутренним режимным факторам: температуре и давлению свежего пара, давлению в теплофикационном и конденсационном отборах, температуре подачи сетевой воды и другим. В итоге паровая характеристика в линейном приближении будет иметь вид:

D_o = a₀ + a\N₃ + а₂0г + <поправки>. (1)

Использование точной характеристики (1) при моделировании не представляется возможным, так как невозможно учесть все текущие значения внутренних факторов режимов турбин. Поэтому целесообразно использовать граничную внешнюю характеристику турбины, определенную при оптимальных сочетаниях внутренних факторов, например, по критерию минимума потребления пара:

Во= Ьд + bxN3 + b^Qv

Рассмотрим вопрос определения граничных производственных характеристик узлов на основе данных эксплуатации.

Решение задачи построения граничных характеристик предлагается осуществлять в данной работе на основе двух этапов. На первом этапе на основе решения задачи кластеризации данных из всей совокупности данных эксплуатации выделяются граничные (мажорантные и минорантные).

На втором этапе с использованием граничных данных находятся непосредственно граничные характеристики.

Постановка задачи кластеризации данных на мажорантные и минорантные имеет следующие особенности.

• 1.    Наличие ошибок в измерении значений производственных характеристик элементов сетей и систем.

• 2.    Неполнота информации о производственных характеристиках, содержащихся в данных эксплуатации.

Поэтому решение задачи кластеризации должно включать сглаживание ошибок в данных и регуляризацию постановки задачи.

С учетом сказанного в работе предложена следующая постановка задачи кластеризации, которую для определенности будем рассматривать как выделение мажорантных данных.

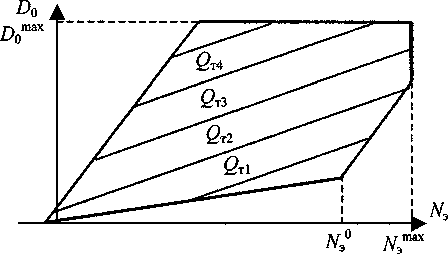
Рис. 1. Паровая характеристика турбины

В основе постановки задачи лежит система неравенств

Py_s\y._s, sel₃;                 (2)

p(a,x_s)>y, :p._s, sel_p,                 (3)

где x_s, y_s - статистические данные о производственных характеристиках: х, - входные данные, y_s - выходные эффекты; р(а,х.) - дискриминантная функция, выделяющая мажорантные данные из общей совокупности данных; а - вектор искомых параметров дискриминантной функции; ц, - характеристическая функция соответствующего 5-го неравенства (ц₄ -1, если неравенство выполняется; щ = 0 в противном случае); 1₃, /_р - соответственно индексное множество экспериментальных и регуляризующих данных.

Система неравенств (2)-(3) соответствует двум наборам данных, используемых при решении задачи. Набор данных эксплуатации (1₃) отражает результаты наблюдений реальных значений про-

Серия «Компьютерные технологии, управление, радиоэлектроника», выпуск 5

изводственных характеристик элементов сетей и систем в процессе эксплуатации. Регуляризующий набор данных (/р) является дополнительным и используется для восполнения недостающей информации, которой не содержится в данных реальных наблюдений. В качестве регуляризующих наборов данных могут быть использованы нормативные данные, экспертные оценки и др.

Выбор значений вектора параметров дискриминантной функции (а) осуществляется по критерию максимального взвешенного числа выполненных неравенств (2)—(3):

A^Q-^IX+^IX Хе[0,1], sel3 selp при ограничении

^маж = £ (1-И5)^^оТ+^пов=^доп.    (4)

Здесь X - вес регуляризующих данных; N^ⁿ - минимально допустимый размер обучающей выборки данных, необходимых для определения неизвестных значений вектора a (jV™ = dima+ 1); N_n0B - размер поверочной выборки данных, на которых оценивается точность построенной дискриминантной функции (jV_nos > 1).

Вес регуляризующих данных X выбирается из условия корректности постановки задачи кластеризации. При X = 0 задача решается только на экспериментальных данных и в общем случае является некорректно поставленной. При X = 1 задача решается только на регуляризующих данных и по определению является корректно поставленной. Однако при этом получаемое решение не отражает реальные экспериментальные данные. Поэтому при выборе значения коэффициента X необходимо задавать минимально возможное значение, при котором сохраняется корректность постановки задачи.

Алгоритм решения задачи кластеризации следующий.

• 1.    Задаются начальные значения веса регуляризующих данных X и весов данных а, = 1.

• 2.    Методом взвешенных наименьших квадратов решается система уравнений

• 3.    Вычисляется превышение выходного эффекта у, над значением дискриминантной функции при входных факторах x_s

• 4.    Определяются веса данных

• 5.    Данные, которые имеют вес a_s = 1 являются мажорантными. Подсчитывается их количество N^.

• 6.    Число мажорантных данных К_маж сравнивается с допустимым числом данных N_ron.

Р(а,^.) = у_$ :(1-Х)а,, sel₃;

р(а,хД = ys Aas, selp.

^ys = У, ~Р^х,).

[1, если Ay, > 0;

а, =<

[у, если Ду8 < 0, где у определяет скорость сходимости алгоритма. При у = 0 - максимальная сходимость, однако при этом на первой итерации решения может выполняться неравенство N^ < N№. При у = 1 решение заканчивается на первой итерации, и в качестве мажорантных точек являются те, что лежат выше средней характеристики. Величина у в общем случае выбирается из условия выполнения ограничения (4).

Если на первой итерации решения 7VM„ < ^доп, то постановка задачи некорректна и необходимо дополнить число регуляризующих данных. Если данное неравенство выполняется на итерации # 1, то необходимо вернуться к значениям переменных на предыдущей итерации.

Если Ацаж > 7УД0П, то осуществляется переход к решению задачи взвешенных уравнений (к п. 2 алгоритма).

Решением задачи кластеризации является множество мажорантных данных, по которым затем методом наименьших квадратов строится непосредственно граничная характеристика.