Методика использования искусственных нейронных сетей с целью идентификации параметров движения летательных аппаратов

Повседневная1 практическая2 деятельность дает огромное число примеров, показывающих, что определение тех или иных интересующих нас величин производится опытным путем на основе измерений. Наиболее типичной ситуацией подобного рода является проблема определения совокупности величин, характеризующих процессы полета летательного аппарата (ЛА) или его натурной модели.

В частности, при проведении испытаний могут определяться параметры движения ЛА, параметры, характеризующие действующие силы и моменты. После того как эксперимент закончен, наступает этап обработки информации, в результате чего определяются (оцениваются) все неизвестные параметры.

Сами математические методы, с помощью которых обрабатывается измерительная информация, являются весьма общими и их можно применять в самых разнообразных ситуациях при решении задач, имеющих подчас совершенно различное физическое содержание. Основным признаком, по которому эти задачи можно причислить к одному общему классу, является возможность описать указанные физические процессы системой обыкновенных дифференциальных уравнений. В математике подобные процессы и явления принято называть гладкой динамической системой, а группу параметров, характеризующих развитие и протекание процесса или явления, – состоянием динамической системы [1].

Рассмотренную задачу можно интерпретировать как задачу определения состояния динамической системы по измерениям. Отметим, что в литературе наряду с термином «оценивание состояния» используется также термин «параметрическая идентификация». Указанные понятия весьма близки по своему содержанию, а иногда просто идентичны. Поэтому в дальнейшем будем использовать термин «параметрическая идентификация» [7].

Под идентификацией будем понимать процедуру построения оптимальной (наилучшей) в определенном смысле математической модели объекта по результатам измерений [6].

ВЕСТНИК 2014. ВЫПУСК 4

Известна (построена по априорным данным) математическая модель движения ЛА dY --- — = F (x, Y, Л), dx

где x - независимая переменная (время, координата или какой-то монотонно изменяющийся параметр);

Y = [ У ] , ^ , y_n ] - вектор фазовых координат движения ЛА;

Л = [ Л , - , Л г ] - вектор идентифицируемых параметров, характеризующих состояние ЛА и среды;

F = [ F , ^ F_n ] - вектор-функция правых частей дифференциальных уравнений, описывающих движение ЛА [2].

...

Вектор начальных значений Y ( x = 0) = Y ₀ , где Y 0 = [ У 1₀ ,У ₂₀ ,..., y n ₀ ] . Этот вектор подлежит определению.

ВЕСТНИК 2014. ВЫПУСК 4

Известна зависимость между независимой переменной, вектором параметров движения ЛА и вектором измеренных параметров (называемая уравнением измерений):

Z = G [ x , Y ( x ), W ( x , Y ) ] , (2) где Z = [ z 1 , z ₂ ,..., z p ] - вектор измеренных параметров (результатов измерений);

G = [ g i , g 2 ,..., g p ] - вектор-функция, определяющая связь независимой переменной x , параметров движения ЛА и измерительных шумов;

W = [ W j , w ₂ ,..., w n ] T - вектор составляющих шума с известными характеристиками.

При W = 0 функция G представляет собой измеряемый вектор параметров движения ЛА. Этот вектор был бы результатом измерений, если бы измерения были абсолютно точными.

Определению по измерениям подлежит вектор B =[ bj,b 2 ,..., b ]^т = [ У ю,..., y „ 0 , ^Л J ^,...^, Л ] T , q = = n + r , составляющими которого являются компоненты векторов Y и Л . Обычно измерения движения проводятся дискретно в точках некоторых фиксированных значений независимой переменной x , ( i = 0,1,..., k ) , причем, как правило, имеет место неравенство k >  n . _

Для отыскания оценки вектора B задается критерий оптимальности идентификации (функция качества оценки)

_ Ф ( B ) = Ф[ k , Z , Z ( x , , B ), P ( x , ) ] , (3 ) где Z , - вектор результатов измерений в точке x , ;

Z ( x , , B ) - расчетное значение измеряемого вектора, т.е. вектор G ( x , )| W = 0;

P ( x ) - весовая матрица измерений.

Выбор структуры (вида) функции Ф( B ) субъективен [3].

Для решения поставленной задачи предлагается использовать искусственные нейронные сети (ИНС).

Вне зависимости от способа реализации (аппаратной или в виде эмуляторов для обычных компьютеров), ИНС проявляют следующие свойства, необходимые для решения широкого круга технических задач:

• 1.    Обучение. Искусственные нейронные сети могут изменять свое поведение в зависимости от условий внешней среды, т.е. адаптироваться. После предъявления входных сигналов (возможно, с соответствующими выходами) нейронные сети самонастраиваются, чтобы обеспечить требуемую реакцию.

• 2.    Обобщение. Реакция сети после обучения может быть до некоторой степени нечувствительна к небольшим изменениям входных сигналов. Эта особенность выделять образ сквозь шум и искажения позволяет преодолеть требования строгой точности, предъявляемые обычным компьютерам. Важно отметить, что нейронная сеть делает обобщения автоматически благодаря своей структуре, а не с помощью «человеческого интеллекта», представленного в форме специально написанных компьютерных программ.

• 3.    Абстрагирование. Нейронные сети обладают способностью извлекать сущность из входных сигналов, т.е. оперировать с данными, которые не возникали в процессе обучения.

В общем случае ИНС может рассматриваться как направленный граф со взвешенными связями, в котором узлами являются элементарные процессорные элементы - искусственные нейроны. По архитектуре связей ИНС могут быть разделены на два основных класса: сети прямого действия, в которых графы не имеют петель, и рекуррентные сети, или сети с обратными связями, которые являются динамическими, так как в силу обратных связей в них модифицируются входы нейронов, что приводит к изменению состояния сети [5].

Наиболее распространенным семейством сетей прямого действия являются многослойные перцептроны, в них нейроны расположены слоями и соединены однонаправленными связями, идущими от входа к выходу сети. Сети прямого действия являются статическими в том смысле, что на заданный вход они вырабатывают одну совокупность выходных значений, не зависящих от предыдущего состояния сети.

Нейроны могут группироваться в сетевую структуру различным образом. Функциональные

Управление, вычислительная техника и информатика

особенности нейронов и способ их объединения в сетевую структуру обуславливают ту или иную парадигму нейронной сети. Для решения задач идентификации и управления наиболее адекватными, без сомнения, являются многослойные нейронные сети (МНС) прямого действия, или многослойные перцептроны [4]. При проектировании МНС нейроны объединяются в слои, каждый из которых обрабатывает вектор сигналов от предыдущего слоя (или входной вектор). Минимальной реализацией является двухслойная нейронная сеть, состоящая из входного (распределительного), промежуточного (скрытого) и выходного слоев. При подсчете числа слоев входной слой обычно не учитывается, так как служит лишь для распределения входных сигналов по нейронам последующего слоя. На рис. 1 представлена структурная схема двухслойной нейронной сети прямого действия. Сигналы в сети распространяются от входа к выходу, связи между нейронами одного слоя и обратные связи отсутствуют.

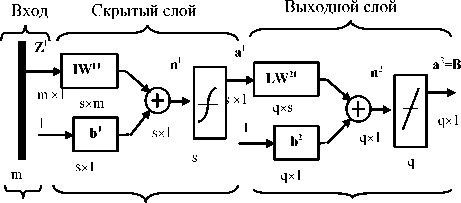
a ¹ = tansig( IW ¹¹ p ¹ + b ¹ )

a ² = purelin( LW ²¹ a ¹ + b ² )

Рис. 1. Структура нейронной сети

Для решения поставленной задачи предлагается на вход И НС передавать значения измерений (вектора Z ) во все моменты времени, когда проводились измерения. На выходе нейронной сети будет искомый вектор B .