Методика исследования глубоких центров по задержке лавинного пробоя p-n-перехода в случае сильной полевой зависимости коэффициентов эмиссии

Лавинный пробой p-n-переходов сильно локализован. Области локального пробоя имеют очень малые геометрические размеры и существенно меньшее напряжение пробоя по сравнению с однородными областями. Эти области сильно локализованного пробоя были названы микроплазмами (МП) [1]. Одним из основных проявлений микроплазменного эффекта в p-n-переходах является импульсный характер лавинного тока. Длительности импульсов и пауз между ними случайны. С ростом приложенного напряжения амплитуда импульсов увеличивается незначительно, но очень сильно возрастает их длительность, и сокращаются паузы между ними. При дальнейшем увеличении напряжения появляются новые микроплазмы. Такой характер протекания тока через микроплазмы приводит к появлению разрывов и изломов на вольт-амперной характеристике p-n-перехода. Наблюдение микроплазменных импульсов может быть затруднено из-за наличия нескольких одновременно работающих микроплазм. При пробое полный ток диода сконцентрирован в области микроплазмы, не смотря на ее малые размеры. Таким образом, напряжение пробоя реального p–n-перехода представляет собой напряжение включения первой микроплазмы VM.

Если на p–n- переход подать прямоугольный импульс напряжения, то будет наблюдаться статистическая задержка пробоя микроплазмы, обусловленная отсутствием в течение некоторого времени в канале микроплазмы носителя, способного дать начало лавине. Кроме того, не каждый носитель, попавший в микроплазменный канал, запустит лавину. Процесс запуска лавины носит случайный характер и определяется вероятностью запуска носителем лавины. При этом считается, что электрическое поле в p–n- переходе мгновенно следует за изменением напряжения. Запускающие носители заряда могут попадать в канал МП, в основном, вследствие четырех механизмов: диффузии из базовых областей, термогенерации носителей в области пространственного заряда (ОПЗ), туннельного эффекта, реэмиссии с глубоких центров (ГЦ). Кроме этих четырех механизмов возможно попадание носителей в канал микроплазмы под действием внешних источников (облучение светом, γ -квантами). Возможно также взаимодействие микроплазм, если они находятся на небольших расстояниях друг от друга. При определенных обстоятельствах, например, слабый фоновой генерации (первые три механизма), четвертый фактор может вносить основной вклад в запуск лавины. Когда концентрация глубоких центров мала, то эмиссия носителей заряда с ГЦ будет влиять лишь на частоту микроплазменных импульсов и статистическую задержку пробоя микроплазмы.

Целью данной работы является усовершенствование разработанной ранее [2, 3] методики исследования глубоких центров в микроплазменных каналах по статистической задержке лавинного пробоя p–n- перехода.

При исследовании вероятности включения микроплазмы при заполнении глубоких центров в микроплазменном канале необходимо точно знать местоположение области эмиссии носителей, участвующих в запуске лавины, так как коэффициент ударной ионизации зависит от электрического поля. На рисунке 1 представлено распределение электрического поля в p–n- переходе при двух напряжениях V M и V m .

Рассмотрим p–n- переход, в котором имеются равномерно распределенные глубокие центры с энергетическим уровнем в верхней половине запрещенной зоны и коэффициент эмиссии электронов с глубоких центров намного больше коэффициента эмиссии дырок e n >>e p . Пусть p–n- переход находится при такой температуре, при которой уровень Ферми в n- базе выше глубокого уровня. Подадим на p–n- переход напряжение V M , равное напряжению включения самой низковольтной микроплазмы. То есть, при самом незначительном увеличении напряжение смещения, через p–n- переход потечет лавинный ток.

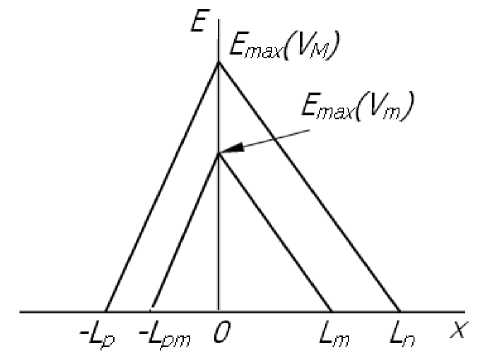
Рис. 1. Распределение электрического поля в p–n -переходе.

На рисунке 2 схематически представлена рассматриваемая структура.

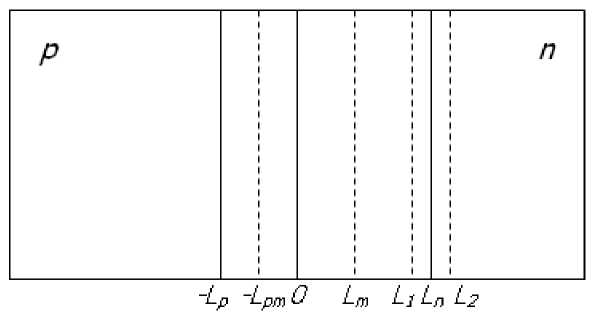
Рис. 2. Схематическое изображение p–n- перехода.

Когда на p–n- переход подано напряжение V m < V M , область пространственного заряда уменьшится до L m , глубокие центры в области от L m до L n заполняются электронами со стороны n- базы. В области от – L p до L m установившееся при V m стационарное распределение заряда не изменяется. При приложении напряжения V 2 > V m , ОПЗ увеличится, соответственно увеличится напряженность электрического поля. Со стороны n- базы граница ОПЗ при этом напряжении соответствует L 2 (рис. 2), со стороны p- области граница ОПЗ при напряжении V 2 не показана, т.к. заполнение ГЦ в этой части ОПЗ не изменяется.

Если существует полевая зависимость коэффициентов эмиссии носителей заряда с глубоких центров, то после изменения электрического поля, изменится распределение зарядов на глубоких уровнях в области от –Lp до Lm, что может внести значительный вклад в вероятность включения микроплазмы. Поэтому при исследовании глубоких центров в области от Lm до Ln (рис. 2) необходимо исключить влияние запуска лавины носителями, эмитированными с ГЦ в области от –Lp до Lm. В связи с этим предлагается проводить измерения статистической задержки микроплазменного пробоя на прямоугольных импульсах напряжения следующего вида (рис. 3).

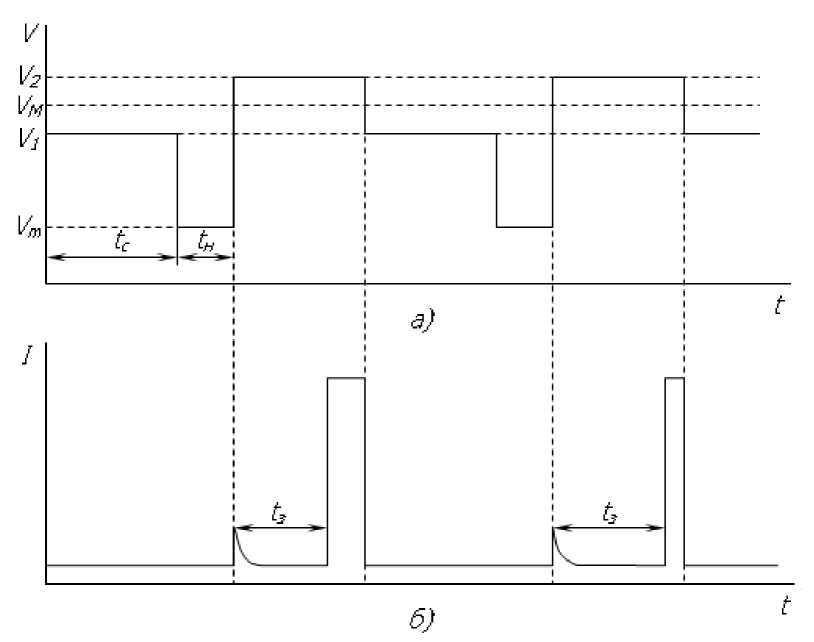
Рис. 3. Форма импульсов напряжения для измерения задержки пробоя: а) напряжение, прикладываемое к диоду; б) ток через диод.

Время t c выбирают таким образом, чтобы в p–n- переходе успевало устанавливаться стационарное состояние ГЦ. Время t н должно быть гораздо меньше времени перераспределения заряда на ГЦ под действием электрического поля в области от – L p до L m (рис.2), и в тоже время, чтобы ГЦ в области от L m до L 1 заполнились основными носителями заряда (электронами) со стороны n- базы. Это можно сделать, так как время перераспределения носителей заряда на ГЦ под действием электрического поля определяется коэффициентами эмиссии носителей заряда с ГЦ, а заполнение ГЦ электронами в области от L m до L 1 при попадании ее в n- базу при снижении напряжения до V m определяется коэффициентом захвата основных носителей заряда на ГЦ, который гораздо больше. Таким образом, можно исследовать влияние на вероятность включения микроплазмы только тех носителей, которые эмитированы из области от L m до L 2 . Для исключения перераспределения заряда ГЦ в области от – L p до L 1 , V 2 –V 1 должно быть много меньше V 2. При этом эмиссия носителей с глубоких центров в области заполнения от L 1 до L 2 должна влиять на вероятность включения микроплазмы. Однако электрическое поле в этой области настолько слабое, что эмитируемые с ГЦ носители не будут оказывать влияние на запуск лавины.

Поэтому предыдущая методика [2], в случае сильной полевой зависимости коэффициентов эмиссии носителей заряда с ГЦ, не позволяла корректно исследовать глубокие центры при заполнении их основными носителями незначительным снижением напряжения на p–n- переходе. Изменяя напряжение V m , можно изменять область заполнения ГЦ основными носителями заряда и исследовать влияние эмиссии носителей с ГЦ на запуск лавины в различных областях p–n- перехода.