Методика исследования пористости образцов с жидкостью рентгеновским компьютерным томографом при одноосном сжатии

PNRPU MECHANICS BULLETIN

Развитие композиционных, сложноструктурированных материалов и изделий ставит вопрос о развитии экспериментальных методов определения напряженно-деформированного состояния (НДС). Неравномерность и негомогенность внутренней структуры ограничивают результаты, получаемыми стандартными экспериментальными методами, и не дают полной картины о работе материала или изделия. Более того, наличие внутренних дефектов, локальная потеря устойчивости могут значительным образом повлиять на получаемые результаты.

На данный момент существует множество экспериментальных методов, позволяющих определить НДС экспериментально, но эти методы в большей степени ограничены оценкой на поверхности исследуемого образца. Обычно в таких методах измеряются перемещения поверхностных точек деформируемых тел как прямыми, так и косвенными методами. Известные соотношения механики твердого тела позволяют связать поверхностные деформации и напряжения, поэтому измерение кинематических параметров является определяющим при исследовании НДС конструкций. Рассмотрим подробнее наиболее распространённые методы.

Широкое распространение получило использование электротензометрических датчиков [1; 2]. Данный метод относится к контактным методам и основан на определении напряжений и деформаций в наружных слоях детали с помощью тензодатчиков, усилителей и регистрирующей аппаратуры. Тензодатчик приклеивается к поверхности исследуемого образца и работает как резистор, при этом поверхностные деформации приводят к изменению площади поперечного сечения резистора, что, в свою очередь, изменяет электрическое сопротивление. Но при этом метод обладает и недостатками, а именно: трудоемкость установки при большом количестве датчиков, большое количество отходящих проводов от тензодатчиков, чувствительность к электрическим и тепловым помехам. Также к минусам можно отнести локальность оценки НДС, то есть предварительно для установки датчиков необходимо выяснить интересующие места, такие как: зоны образования трещин, зоны концентрации напряжений.

К бесконтактным оптическим методам относятся как интерферометрические методы: голографическая интерферометрия, спекл-интерферометрия, так и неинтерферометрические методы: метод фотокорреляции (DIC) и метод фотоупругости [3].

Метод фотоупругости требует изготовление образца из фоточувствительного материала, что, очевидно, снижает применимость для композиционных материалов. Интерферометрические методы требуют использования когерентного источника света, а само испытуемое изделие должно находиться на виброизолирующем стенде, при этом получаемая информация характеризует только поверхностные напряжения [4].

Неинтерферометрические методы определяют деформацию на поверхности изделий путем сравнения интенсивности цвета пикселей до и после деформации. Двумерный метод фотокорреляции является визуальным неинтерферометрическим методом определения НДС на поверхности испытуемого образца, основным принципом которого является поиск одинаковых участков изображения (пикселей) на двух разных изображениях, до и после деформации соответственно [5; 6].

Для вычисления перемещения заранее выбранной реперной точки на изображении выделяется квадратный участок пикселей с центром в какой-то точке. Далее производится нагружение образца с последующей съемкой, а с помощью специальных алгоритмов определяются перемещения реперных точек в разные моменты времени. К недостаткам метода можно отнести то, что его реализация и получение каких-либо реальных результатов напрямую связано с качеством оборудования, экспериментального стенда и окружения, в котором проводится фо-то/видеосъемка. Метод чувствителен к возможным вибрациям, засветам и шумам на итоговых изображениях.

Описанные выше методы характеризуются исследованием механических свойств на некотором поверхностном слое образцов, без оценки внутренней структуры. Кроме того, для современных материалов внутренняя структура является зачастую определяющей.

Под внутренней структурой часто принимается пористость материала. Она характеризуется комплексом параметров: формой, объемом, протяженностью, плотностью расположением пор в материале и многим другим. Но стоит остановиться на открытом или закрытом характере пор. Открытые поры – это поры, которые сообщаются с поверхностью тела и участвуют в фильтрации жидкости или газа при наличии градиента давления на пористом теле. Закрытая пора не сообщается с поверхностью тела. Существует множество методов для исследования пористой структуры материала с открытыми порами, такие как визуально-оптические, методы, основанные на световой микроскопии, капиллярные, методы термопорометрии, жидкостной и газовой волю-мометрии, заполнения пор жидкостью и др. Однако только методы, основанные на анализе рассеяния излучений (характере изменения интенсивности при прохождении через материал) способны дать оценку пористой структуры материала не только с открытыми порами, но и с закрытыми. К ним можно отнести методы, использующие ультразвуковое излучение, рентгеновское излучение (КТ или РКТ) [7–10].

Ультразвуковая диагностика внутренней структуры основывается на том, что колебания с высокой частотой (примерно 20 тысяч Гц) способны проникать в материал и отражаться от дефектов [11; 12]. Узконаправленная волна, создаваемая дефектоскопом, проходит сквозь проверяемое изделие. При наличии дефекта она распространяется с отклонениями, которые можно зафиксировать на экране прибора. Показания, полученные в ходе

УЗК, позволяют узнать информацию о характере выявленного дефекта. Например: по времени прохождения ультразвукового сигнала – измеряется расстояние до неровности, по амплитуде колебания отражённой волны – примерные размеры дефекта. К основным недостаткам данного метода можно отнести:

– не любой материал пригоден под использование данного метода (высокий коэффициент затухания, разнородность);

– требуется тщательная подготовка поверхности проверяемого изделия, чтобы между ней и прибором не было даже малейшего воздушного зазора;

– во многих случаях этот метод не позволяет получить информацию об истинных размерах дефекта;

– трудности с анализом изделий сложной формы и малых размеров.

Одним из наиболее распространённых современных методов оценки внутренней структуры материала является компьютерная томография (КТ) вообще и рентгеновская компьютерная томография (РКТ) в частности. Множество исследований направлено на разработку методов исследования структуры материала по данным компьютерной томографии [13; 14]. Среди них можно выделить методы, основанные на некоторых осредненных величинах (определение пор по числу Хаунсфилда), и методы, основанные на восстановлении геометрии (сегментация) [15–22]. Во время процесса сканирования на РКТ измеряется затухание рентгеновского луча при его прохождении через материал образца. Когда параллельный монохроматический рентгеновский пучок проходит через вещество с одинаковой плотностью и одинаковым атомным номером, он экспоненциально затухает. Линейный коэффициент затухания μ определяется как относительное уменьшение интенсивности рентгеновского излучения на единицу длины этого материала. Как правило, линейный коэффициент затухания нормализуется к коэффициенту стандартного материала (например, воды или воздуха). Это означает, что каждому материалу присваивается неизменный номер, который помогает рассчитать номер другого материала и определяется как единицы Хаунсфилда ( HU ):

HU =

μ material - μ

water

■ 1000.

μ

water

- μ air

По числу Хаунсфилда нетрудно отделить материал образца от его пор. Сегментация пор в томографии происходит после сканирования РКТ, когда на диаграмме распределения числа HU определяются n диапазонов, по которым можно определить, какой диапазон соответствует какому материалу. Несмотря на развитие как самих РКТ, так и методов обработки данных, большинство исследований над образцами производятся в статике, то есть без приложения внешней нагрузки.

Поэтому целью настоящего исследования стала разработка метода исследования внутренней структуры и напряженно-деформированного состояния образца при одноосном сжатии с применением РКТ.

1.    Материалы и методы 1.1.    Описание работы

Для исследования внутренней структуры образцов под действием внешней нагрузки была спроектирована и изготовлена специальная оснастка. Для интерпретации и анализа получаемых результатов была сформулирована методика проведения эксперимента. Была разработана установка для проведения эксперимента, на которую получен патент на изобретение [23].

Для исследования внутренней структуры и механических свойств были спроектированы типовые образцы с порами [24]. Изготовление образцов производилось на фотополимерном 3D-принтере. Было спроектировано и изготовлено шесть образцов: один сплошной, два со сферическими порами, три с эллиптическими порами. Подробнее геометрия образцов и метод их изготовления описаны в п. 1.4. Изготовленные образцы подвергались предварительной подготовке, согласно п. 1.3. Затем образец помещался в разработанное устройство [25]. Устройство вместе с образцом фиксировались в патроне РКТ. В ходе экспериментов каждый образец нагружался, и производилась съемка. Полученные в результате экспериментов данные обрабатывались согласно описанной ниже методике для последующего анализа.

• 1.2.    Описание устройства

Для исследования образцов было спроектировано устройство для передачи осевого усилия на образец. Образец 1 на рис. 1 помещается между нижней крышкой 2 и динамометром 4 .

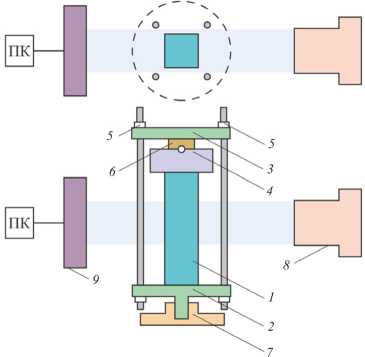
Рис. 1. Устройство для передачи осевого усилия: 1 - испытуемый образец; 2 - нижняя крышка; 3 - верхняя крышка;

4 - динамометр; 5 - гайки; 6 - центровочная шайба с шариком; 7 - патрон томографа; 8 - излучатель рентгеновского излучения; 9 - приемник рентгеновского излучения; ПК - персональный компьютер

Fig. 1. Device for transmitting axial force: 1 - test specimen; 2 - bottom cover; 3 - top cover; 4 - dynamometer; 5 - nuts; 6 - centering washer with a ball; 7 - tomograph cartridge;

• 8 - X-ray emitter; 9 - X-ray receiver; PC - Personal Computer

Сжимающая осевая нагрузка передается через шайбу и центровочный шарик 6 с помощью затягивания гаек 5 на верхней крышке 3 . Динамометром 4 определяется сжимающая нагрузка на образец.

Устройство для передачи осевого усилия устанавливается нижней крышкой в патрон томографа 7 . Исследуемый образец располагается между приемником рентгеновского излучения (экраном) 9 и излучателем рентгеновского излучения 8 . Более полно и подробно оснастка и принцип ее работы описаны в патенте [23].

• 1.3.    Описание проведения эксперимента

Перед проведением эксперимента производилась предварительная подготовка образца. На поверхность каждого образца наклеивалась регулярная сетка из медной проволоки диаметром 90 микрон. Узлы сетки выполняют роль реперных точек. Материал проволоки подобран таким образом, чтобы была возможность легко контрастировать сетку от материала исследуемого образца на полученной компьютерной модели. Малый диаметр сечения проволоки позволял при анализе данных пренебречь жесткостью медной сетки в процессе нагружения.

Для проведения эксперимента необходимо установить устройство с испытуемым образцом в патрон томографа. Для динамометра отмечается нулевая линия нагрузки, замеряется расстояние между верхней и нижней, производится контроль позиционирования исследуемой зоны и установки таким образом, чтобы исследуемая зона находилась в поле сканирования приемника излучателя рентгеновского излучения. После этого производится первое сканирование исследуемого образца компьютерным томографом. На следующем шаге производится последовательная затяжка четырех гаек для передачи осевого усилия на исследуемый образец. После затяжки гаек определяется перемещение верхней крышки и определяется показание динамометра, после чего производится повторное сканирование. Каждый образец подвергается трем шагам нагружения. Затягивание гаек производится непосредственно в томографе, что обеспечивает постоянное позиционирование образца относительно экрана.

Сканирование образцов было выполнено с применением микро-/нанофокусной системы рентгеновского контроля для компьютерной томографии и 2D-инспек-ции Phoenix V|tome|X S240 в лаборатории рентгеновской компьютерной томографии Института геологии и нефтегазовых технологий Казанского (Приволжского) федерального университета. Система оснащена двумя рентгеновским трубками: микрофокусной с максимальным ускоряющим напряжением 240 кВ, мощностью 320 Вт и нанофокусной с максимальным ускоряющим напряжением 180 кВ, мощностью 15 Вт. Для первичной обработки данных и создания объёмной (воксельной) модели образца на базе рентгеновских снимков (проекций) используется программное обеспечение datos|x reconstruction.

В результате проведения серии экспериментов были получены данные: перемещения верхней поверхности образца, прикладываемая сжимающей осевая нагрузка и внутренняя структура исследуемого образца (РКТ-модель). Полученные данные подвергались последующей обработке.

• 1.4.    Описание исследуемых образцов

  • 1.4.1.    Геометрия исследуемых образцов

Спроектированные образцы представляют собой упорядоченный набор физических объемов (схематичное изображение представлено на рис. 2, а ): в продольном направлении 10, в поперечном - 3x3. Физический объем представляет собой куб с ребром 8 мм, в который вписана сфероидальная пора, наполненная жидкостью. Геометрия поры определяется двумя безразмерными параметрами: X, в и Ф, где X - отношение наименьшей полуоси к наибольшей ( b / a ), в - отношение удвоенной наибольшей полуоси к ребру куба (2 a / h ), а ф - угол направления наибольшей полуоси. Схематично физический объем изображен на рис. 2, b . Зная геометрические размеры, можно найти проектную пористость p о (соотношение объема поры и объема элемента-куба). Геометрические характеристики изготовленных образцов приведены в табл. 1.

Таблица 1

Геометрические характеристики изготовленных образцов

Table 1

Geometric characteristics of the fabricated samples

№ образца	b / a	2 a / h	ϕ	p 0 , %
1	0	0	0°	0
2	0,54	0,73	90°	11

а

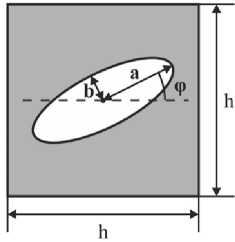
Рис. 2. Изготовление образцов: а - схематичное изображение физических объемов в образце; b - геометрия физического объема

Fig. 2. Sample’s geometry: a -scheme of the sample in terms of physical volumes; b - scheme of the physical volume

• 1.4.2.    Изготовление исследуемых образцов

Изготовление образцов производилось с помощью аддитивных технологий. Был использован фотополимер-ный принтер ANYCUBIC Photon Mono X, в качестве материала применялась фотополимерная смола Anycubic Colored UV Resin, характеристики которой приведены в табл. 2.

Таблица 2

Характеристики фотополимерной смолы Anycubic Colored UV Resin

Table 2

Anycubic Colored UV Resin properties

Наименование характеристики	Величина	Размерность
Длина волны отверждения	405	нм
Вязкость	552	МПа∙с
Плотность в жидком состоянии	1000	гр/см3
Плотность в твердом состоянии	1184	гр/см3
Твердость по Шору	79	D
Удлинение при разрыве	14,2	%
Точность по оси Z	0,01	мм
Прочность на растяжение	23,4	МПа

Размер физического объема составляет 8×8×8 мм. Образец является набором физических объемов, где в поперечном слое 3×3 физических объема, а по продольному направлению - 10. Схематично образец приведен на рис. 2, а . Размер каждого образца составил 80×24×24 мм. Толщина слоя печати по вертикальной оси - 10 мкм.

• 1.5.    Обработка данных

  • 1.5.1.    Определение перемещений поверхностной сетки

Выходными данными сканирования РКТ являются трехмерные массивы с величинами коэффициента рентгеновского ослабления. Структурно среди этих данных можно выделить три объекта: экспериментальная оснастка, образец и поверхностная сетка. Данные о поверхностной сетке сегментируются на основе принципа связности из заданного диапазона коэффициентов рентгеновского ослабления. Для полученного набора сегментированных данных определялись особые точки: углы и узлы сетки [26; 27]. Для автоматизированного определения особых точек использовался метод Харриса [28], модифицированный для трехмерного случая [29; 30]. Опишем кратко метод - введем функцию интенсивности изображения I ( x , y , z ), которая определена в координатах каждого вокселя ( x , y , z ). Функцией интенсивности может быть, например, сумма значений Хаунсфилда в области. Зададим окно W с шагом смещения Δ x , Δ y , Δ z . Тогда изменение интенсивности в окрестности точки ( x , y , z ) при сдвиге на Δ x , Δ y , Δ z определяется следующим образом:

E (Ax, Ay, Az) =

= E w(x,y,z)•(I(x + Ax,y + Ay,z + Az)-1(x,y,z))2,

(x, y, z )eW где w – весовая функция окна.

Разложение изменения интенсивности E около нуля в ряд Тейлора приводит к выражению, суть которого квадратичная форма:

f Ax )

E ( A x , A y, A z ) = ( A x , A y, A z ) • M • A y ,

^Az у где M – автокорреляционная матрица, которая примет вид:

fI2 II IIл x    xy   xz M = E w (x, y, z )• IxIy   Iy    IyIz . (x, y, z )eW II II I2 V x z y z      z J Особые точки в этом случае определяются наибольшими собственными значениями автокорреляционной матрицы. Практический интерес представляют соотношения этих собственных значений, поэтому для вычислительного удобства вводится мера отклика:

R = det M - к •( trace (M)) , где k – эмпирическая константа, которая находится в промежутке от 0,003 до 0,006 [29].

В полученной матрице R необходимо определить локальные максимумы, которые по сути являются особыми точками, то есть углами или узлами сетки.

В работе функция интенсивности была определена как сумма всех коэффициентов рентгеновского ослабления в окне, а в качестве весовой функции было использовано бинарное окно. Выходными данными описанного алгоритма являлись координаты особых точек поверхностей сетки, то есть реперные точки. Определив реперные точки на каждом шаге нагружения, можно определить перемещения относительно начального не-нагруженного состояния. Константа k определялась для заданного снимка на основе тестовых результатов расчета особых точек.

• 1.5.2.    Интерполяция перемещений на внутренний объем

Для определения перемещений в каждой точке образца необходимо интерполировать значения перемещений, полученные с реперных точек. Для этого была построена регулярная сетка внутри компьютерной модели исследуемого образца. Построение производилось таким образом, чтобы каждому элементу сетки соответствовал один физический объем образца. Для интерполяции использовалась линейчатая аппроксимация вида:

U i = a , + a^J ₂x₁ + a j y i + a^ z i + a ^ x i y i + a^J ₆x₁z₁ + a ^ y i z i + a^ x i y i z i , где α ^j – неизвестные коэффициенты.

Регулярная сетка строилась на нулевом шаге нагружения. Результаты перемещений поверхностной сетки на каждом шаге нагружения интерполировались на регулярную сетку исследуемого образца. Для интерполяции перемещений использовалась линейчатая аппроксимация:

<

U ¹

U ²

U ³

= a l + « 2 x i + a ( y i + a ( z i + a ( xy + a 1 ₆ x i z i + a ( y i z i + « 8 x i y i z i

22    2     2    2      2      2      2

= a , + a ₂ x i + a ₃ y i + a ₄ z i + a ₅ x i y i + a ₆ x i z i + a ₇ yz + a ₈ x i y i z i

3   . 3        . 3        .      3        . 3                   3                   3                   3

= a , + a ₂ x i + a ₃ y i + a ₄ z i + a ₅ x i y i + a ₆ x i z i + a ₇ yz i + a ₈ x i y i z i

В рамках малости полученных перемещений в узле каждого элемента деформации рассчитывались по формуле Коши:

1 f dUi  dUj)

.

2 ( dxj    dx1 J

В выражении использовались интерполированные перемещения.

• 1.5.3.    Подсчет структурных характеристик при нагружении

Для количественной оценки структурных изменений образца в каждом элементе объемной сетки определяется пористость и объемная деформация. Для определения приведенных характеристик данные внутри каждого элемента сегментируются. В данном случаи пористость можно определить по формуле:

Ф к =

^ w k ( ^x j , y_p z j )- I B ( ^x j , y_p z j )

E w k ^{( x} j , yr z j )

где индекс k определяет номер физического объема, индекс – шаг нагружения, w^k ( x , y , z ) – весовая функция окна, определяющая соответствующий физический объем k , I B – функция интенсивности, точка – умножение по Адамару, а суммирование проводилось по всем точкам окна.

То есть пористость определяется прямым методом по данным РКТ: отношение количества вокселей в поре к общему количеству вокселей в физическом объеме.

Объемная деформация определяется как изменение объема куба с порой (физический объем) dV^k , где k – индекс определяющий номер соответствующего физического объема. Объемная деформация может быть найдена как:

kk gk = dV i dV 0 dV0k    , где – индекс, отвечающий за шаг нагружения, а 0 – начальное и ненагруженное состояние образца.

2.    Результаты и обсуждение

В рамках исследования были испытаны образцы, описанные в разделе «Материалы и методы». Результаты, полученные для сплошного образца, не противоречат известным моделям и представлениям и служат в большей степени подтверждением работоспособности метода. Поэтому основной акцент в обсуждении сделан на образце №2. Образец, как было описано ранее, представляет собой пористую конструкцию, поры были заполнены флюидом – фотополимерной смолой, проектная пористость составляет 11 %. Геометрия поры представляет собой сфероидальную форму со следующими геометрическими соотношениями: отношение наименьшей полуоси к наибольшей ( b / a ) составляет 0,54, отношение удвоенной наибольшей полуоси к ребру куба (2 a / h ) составляет 0,73 и угол наклона ϕ равен 0°. Размер ребра вокселя был равен 0,0807 мм

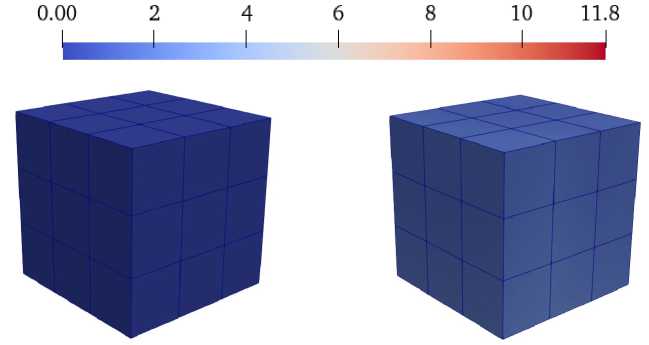
Здесь и далее результаты приведены для внутренней сетки для следующих шагов нагружения: 0-й шаг нагружения соответствует начальному положению образца без приложенной силы (0 Н), 1-й шаг соответствует нагружению силой 1440 Н, 2-й шаг соответствует нагружению силой 4104 Н, 3-й шаг соответствует нагружению силой 6739 Н. Так, на рис. 3 приведены результаты полных перемещений элементов в процессе нагружения.

а                              b

c

Рис. 3. Продольные перемещения (в вокселях) элементов на: а – 0-м шаге; b – 1-м шаге; c – 2-м шаге; d – 3-м шаге нагружения

d

Fig. 3. Longitudinal displacements of elements at: a – 0th step; b – 1st step; c – 2nd step; d – 3rd step of loading

Отметим, что для первых двух активных шагов нагружения распределение поля полных перемещений равномерно (рис. 3, b, c). На последнем шаге нагруже- ния отмечаются локальные максимумы перемещений на нижнем слое (рис. 3, d). Стоит отметить, что между 3-м и 4-м шагом нагружения происходила потеря устойчивости образца. По причине потери устойчивости возникают изгибные составляющие перемещений, что и приводит к неравномерности поля перемещений в продольном направлении. Возникновение потери устойчивости можно объяснить наличием пор, заполненных флюидом, которые ведут себя как абсолютно жесткие включения, так как поры заполнены несжимаемой жидкостью.

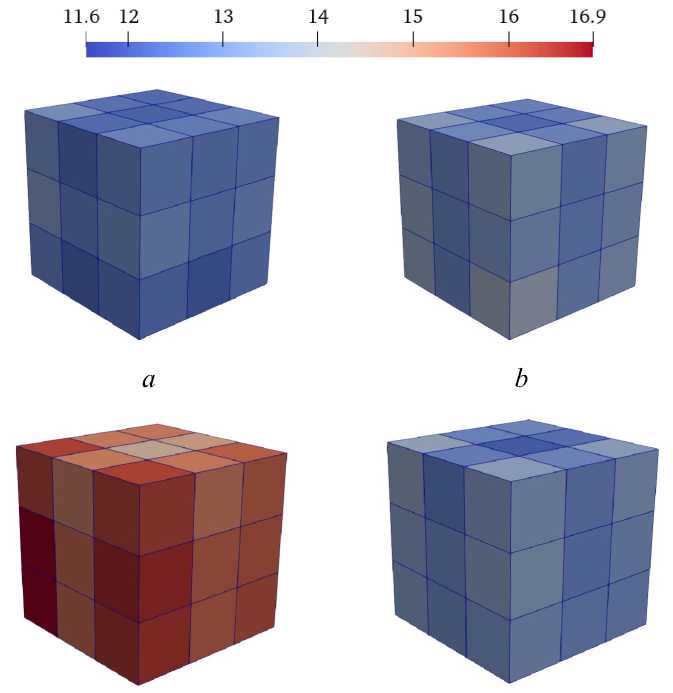
На рис. 4 приведены результаты изменения пористости в элементах. Неравномерность пористости в элементах на 0-м шаге испытаний, связана с дефектами изготовления и погрешностями при сегментации. Однако пористость всего образца незначительно отличалась (относительное отклонение порядка 8 %) от проектной.

d

c

Рис. 4. Пористость (%) в элементах на: а – 0-м шаге; b – 1-м шаге; c – 2-м шаге; d – 3-м шаге нагружения

Fig. 4. Porosity in elements at: a – 0th step; b – 1st step;

c – 2nd step; d – 3rd step of loading

Примечательно, что до 2-го шага нагружения (4104 Н) отмечается возрастание пористости. Это можно объяснить тем, что внутри поры находится смола, которая при нагружении работает как несжимаемая жидкость, а за счет объемной деформации материала вокруг поры происходит увеличение величины расчетной пористости. То есть объем поры остается постоянным, а объем материала вокруг нее уменьшается. На последнем же шаге нагружения происходит локальное разрушение пор, что приводит к вытеканию жидкости и, как следствие, к увеличению пористости. С целью проверки этой гипотезы был проведен анализ объемной деформации.

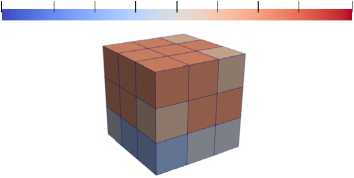
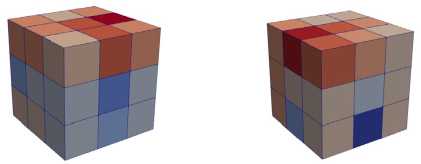
На рис. 5. приведены данные об объемных деформациях в каждом элементе.

0.032 -0.025 -0.02 -0.015 -0.01 0.005 0 0.005 0.012

а

b

c

Рис. 5. Объемная деформация в элементах на: а – 1-м шаге; b – 2-м шаге; c –3-м шаге нагружения

• Fig. 5.    Volumetric strain in elements at: a – 1st step;

b – 2nd step; c – 3rd step of loading

До второго нагружения, хоть и неравномерно, но объемная деформация возрастает, а на последнем шаге уменьшается. Это можно связать с возникновением изгибающей составляющей при испытаниях.

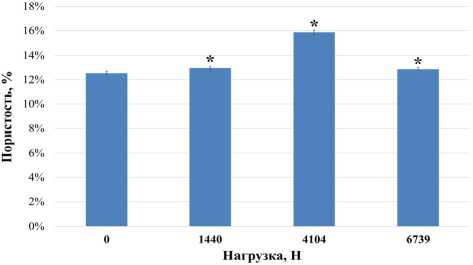
Рис. 6. Средняя пористость по элементам

• Fig. 6.    Average porosity

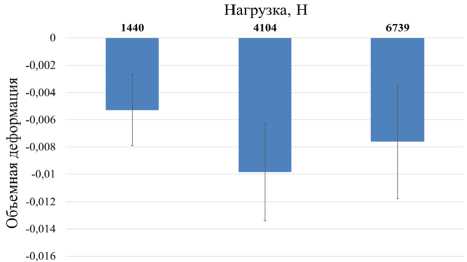
Рис. 7. Средняя объемная деформация по элементам

• Fig. 7.    Average volumetric strain

На рис. 6 и 7 приведены диаграммы с осредненны-ми по элементам значениями пористости и объемной деформации. При оценке осреднённых по всему объему величин пористости можно отметить, что доверительные интервалы малы, а значит распределение пористости почти постоянно по объему. Парный тест Стьюдента (p<0,05) показал статистическое отличие пористости в нагруженном состоянии от начального. Величины доверительных интервалов для пористости и объемной деформации на каждом шаге нагружения приведены в табл. 3.

Таблица 3

Величины доверительных интервалов пористости и объемной деформации

Confidence intervals for porosity and volumetric strain

Table 3

Величина нагрузки, H	Пористость, %	Объемная деформация
0	12,534 ± 0,141	–
1440	12,949 ± 0,163	–0,00528 ± 0,00262
4104	15,854 ± 0,205	–0,00983 ± 0,00359
6739	12,859 ± 0,146	–0,0076 ± 0,00416

Осреднённые по объему величины объемной деформации, напротив, имеют большие размахи, что указывает на неравномерность их распределения. При этом наблюдается возрастание абсолютных величин объемной деформации вплоть до третьего шага нагружения, после которого абсолютные величины объемной деформации падают. А значит, физические объемы возвращаются к первоначальным значениям. Распределение пористости и объемной деформации по шагам нагружения подтверждают гипотезу о влиянии несжимаемой жидкости и дополняют объяснения возрастания пористости при нагружении.

Заключение

В работе были спроектированы и изготовлены экспериментальные образцы, для каждого проведены испытания на сжатие. Испытания проводились согласно авторской методике.

Испытания образца со сфероидальными порами с жидкостью показали возрастание величины пористости при нагружении. Анализ объемной деформации позволил объяснить этот факт. Авторы выдвигают гипотезу, что при нагружении объем поры с жидкостью остается постоянным, но объем материала вокруг поры уменьшается, что и приводит к увеличению величины расчетной пористости.

Авторами планируется провести эксперименты аналогичных образцов с различной геометрией пор. Также авторы планируют теоретически изучить механизм нагружения материала с закрытыми порами с флюидами, дать оценки напряженно-деформированного состояния, критической силы потери устойчивости.

Стоит отметить, что разработанное устройство и методы демонстрируют практическую применимость для экспериментального исследования пористых неоднородных образцов. Приведенный пример ярко иллюстрирует возможности, которые предоставляет методика.