Методика исследования влияния высших гармонических напряжений на режимные параметры синхронного генератора с постоянными магнитами

В настоящее время все большее применение находят синхронные генераторы с постоянными магнитами, управляемые преобразователями частоты. Особенно широкое распространение они получили в ветроэлектрических установках (ВЭУ) крупных мощностей. Эти генераторы могут быть высоко-и низкоскоростными (так называемыми Ringgenerator) для безредукторных ВЭУ [1].

Мощность современных частотно-управляемых синхронных машин с постоянными магнитами достигла таких уровней (5–6 МВт), что они могут быть с успехом применены и на транспорте, в том числе и морском, в качестве двигателей и генераторов.

В общем случае почти все преобразователи частоты для этих синхронных машин выполняются на базе силовых IGBT-транзисторов либо на базе полностью управляемых силовых GТО-тиристоров.

На схеме подключения полностью управляемого преобразователя частоты [2] на IGBT-транзисторах на статорную обмотку высокоскоростного синхронного генератора с постоянными магнитами (рис. 1) используются следующие обозначения: ПД – приводной двигатель (например, дизель); Ред. – редуктор; И – инвертор напряжения; В – выпрямитель; СГ с ПМ – синхронный генератор с постоянными магнитами; ПЧ – преобразователь частоты; L и C – индуктивности и емкости фильтра Ф; Тр с – трансформатор связи с энергосистемой ( U c ).

Рис. 1. Схема подключения преобразователя частоты на статорную обмотку синхронного генератора с постоянными магнитами Fig. 1. The connection diagram of the frequency inverter to the stator windings of the permanent magnet synchronous generator

Необходимо отметить, что современные преобразователи частоты оснащены системой управления, выполненной на базе синусоидальной широтно-импульсной модуляции (ШИМ). При этом в специальной литературе можно найти различные технические решения, позволяющие посредством некоторого усложнения системы управления достичь еще большего снижения величины и числа гармонических составляющих напряжения на выходе преобразователя, приближая его к синусоидальной величине.

В настоящей статье продемонстрированы работоспособность и эффективность разработанной методики исследования влияния высших гармонических составляющих напряжения на режимные параметры синхронного генератора с постоянными магнитами (электромагнитный момент, токи, мощности). Нижеприведенный гармонический состав выходного напряжения преобразователя частоты с ШИМ-управлением в каждом конкретном случае может быть и несколько другим. Но это ни в коей мере не скажется на востребованности и достоверности разработанной методики исследования.

Материалы и методы

Гармонический состав выходного напряжения инвертора с синусоидальным ШИМ при работе его на смешанную нагрузку представляет собой зависимость амплитуд гармонических составляющих выходного напряжения от величины коэффициента модуляции для различных гармоник при разных значениях отношений несущей частоты к частоте модуляции. Для классической системы управления с синусоидальной ШИМ примем его таким, как это приведено, например, в работе [3]: при значении коэффициента ε, f показывающего отношение несущей частоты f к частоте модуляции F , равном ε = нес ≥ 10 , кривые Fм гармонического состава выходного напряжения инвертора с синусоидальной ШИМ имеют вид, представленный на рис. 2.

На рис. 2 изображены зависимости величин амплитуд гармонических составляющих, отнесенных к величине опорного напряжения Е , которое формируется на выходе выпрямителя В (с незначительной погрешностью можно считать, что E = U _баз = 2 й нф _нф , где и нф — фазное напряжение генератора). При е = 12, если, например, принять частоту модуляции равной F = 50 Гц, несущая частота будет равна f = 600 Гц. Тогда в соответствии с кривыми (рис. 2) помимо основной гармоники в кривой напряжения будут присутствовать 8-я, 10, 11, 13, 14 и 16-я гармонические составляющие.

Необходимо отметить, что в инверторе с синусоидальной ШИМ можно регулировать амплитуду выходного напряжения, изменяя при постоянной величине входного напряжения лишь глубину модуляции µ (рис. 2).

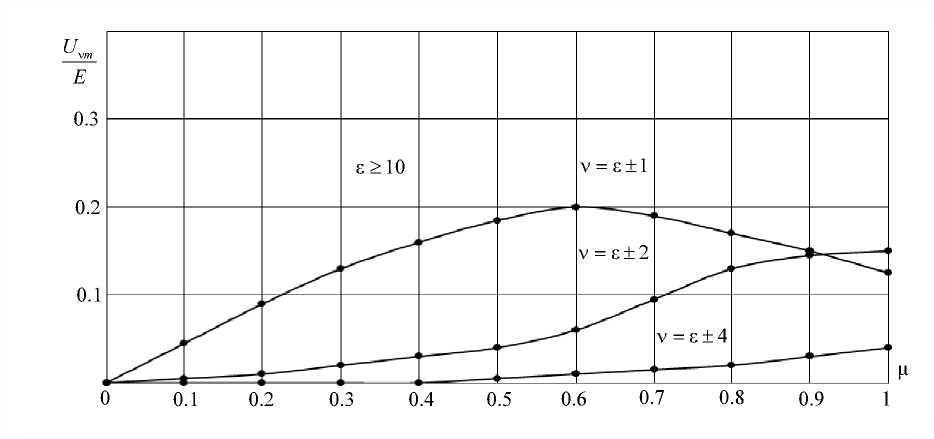
Рис. 2. Кривые гармонического состава выходного напряжения инвертора с синусоидальной ШИМ

Fig. 2. The curves of the harmonic composition of the output voltage of the inverter with sinusoidal PWM

Тогда можно ограничиться наличием неуправляемого выпрямителя, однако при этом нельзя обмениваться активными и реактивными мощностями между источником питания и нагрузкой, поэтому для указанных машин применяется схема, изображенная на рис. 1 (с полностью управляемым выпрямителем). В этом случае частота тока на выходе может регулироваться от нуля до максимума выходным преобразователем (инвертором), соединенным с обмоткой статора генератора, а амплитуда выходного напряжения от 0 до максимального значения – входным преобразователем (выпрямителем), соединенным с выходом питающего трансформатора. При этом глубина модуляции µ остается постоянной и равной максимальному значению µ = 1.

В работах [4; 5] представлена разработанная нами математическая модель частотно-управляемой синхронной машины с постоянными магнитами. Суть ее состоит в том, что известные уравнения Парка для синхронных машин, которые записаны в осях d , q , вращающихся со скоростью ротора машины, преобразованы таким образом, чтобы в них появилась возможность учесть изменение амплитуды и частоты напряжения, подводимого к статорной обмотке машины. Помимо этого, в данных уравнениях введен коэффициент, учитывающий магнитную энергию постоянных магнитов машины, приходящуюся на единицу объема, или при малых значениях остаточной магнитной индукции он трактуется как коэрцитивная сила магнитов.

pY, = [/, - co w -ri, , p ds       ds       r т qs s ds , pY = U + co w , - r i , p   qs       qs       r т ds     s qs ,

PV dr

r e ~ Vdr +

r qr x ad- i„. + -rdr- M

x dr

x dr

qs

x dr

f,

r qr

PTq, = ---V, ^x qr

qr

+

r

x qr aq i

^x qr

qs

,

pa = m r ,

pm_v = —m r

T _j

ПД

--m.

T j

эм ,

m эм

= ^V ds i qs

V qs ds

,

i _qs

x _dr

x ds x dr

— Vds x _a ² _d

x _dr

x _ad

x ds x dr

2 x _a ² _d

M f

x _ad

x ds x dr

— Vdr ^, x _a ² _d

i _qs

x qr

x qs x qr

e

2 x _ad

т

qs

e

x _aq

x qs x qr

e

2 x _aq

т qr ,

^U ds

= ^{0,707 k} us [cos ( k fs ^T ) ( cos a

e

sin a ) - sin ( k f t ) ( cos a + sin a

,

U _qs = 0,707k _us [cos ( k f_s t ) ( cos a + sin a ) + sin ( k _fs t ) ( cos a e sin a )

В системе уравнения (1) приняты следующие обозначения: р – символ дифференцирования по синхронному времени τ = 314 t , где τ – время, рад, t – время, с, т. е. 1 с соответствует 314 рад; ψ _ds , ψ _qs , ψ dr , ψ qr – потокосцепления статорных и роторных контуров машины, о. е.; U ds , U qs – составляющие вектора статорного напряжения машины, учитывающие изменения (регулирование) амплитуды k us и частоты k fs напряжения, подводимого к статорной обмотке машины от выхода преобразователя частоты; i _ds , i _qs , i _dr , i _qr – токи статорной и роторной обмоток по осям d , q ; ω r – угловая частота вращения ротора, о. е.; M f – коэффициент, учитывающий магнитную энергию постоянных магнитов синхронной машины, отнесенную к единице объема, M f = 1 – значение энергии магнитов, способное при холостом ходе синхронного генератора обеспечить ЭДС на его зажимах, равную E _xx = 1; α – угол между осями d , q , вращающимися со скоростью ротора ω _r , и неподвижными в пространстве осями; m ПД – вращающийся момент приводного двигателя (при работе синхронной машины в режиме генератора) или тормозной момент рабочего механизма (при работе двигателя); m _эм – электромагнитный момент синхронной машины; r _s – активное сопротивление статорной обмотки; r dr , r qr – активные сопротивления роторных демпферных обмоток по осям d , q ; х dr , х qr – полные индуктивные сопротивления обмотки ротора по осям d и q ; х аd , х аq – сопротивления взаимоиндуктивности по осям d и q ; х _ds – полное индуктивное сопротивление статорной обмотки машины; T j – инерционная постоянная ротора СМ и первичного двигателя, рад.

Два последних уравнения системы (1) запишем в виде

U ds = 0,707k us cos( k fs t)(cos a - sin a) - 0,707k us sin( k fs t)(cos a + sin a), U qs = 0,707 k us cos( k fs t)(cos a + sin a) + 0,707 k us sin( k fs t)(cos a - sin a).

В уравнении (2) k _us = U _s / U _баз – относительное значение модуля напряжения на выходе преобразователя (т. е. на зажимах статорной обмотки синхронной машины); k fs = f / f баз – относительное значение частоты тока (напряжения) на выходе преобразователя.

Если в соответствии с рис. 2 описать кривую напряжения с учетом гармонических составляющих, то она с учетом основной гармоники запишется в виде

A 1 = 0,9sin( k _/s t ) - 0,035sin(8 k _/s t ) + 0,15sin(10 k _/s t ) - 0,125 sin(1 I k _/s t ) + + 0,125sin(13 k _/s t ) - 0,15sin(14 k _f$ t ) + 0,035sin(16 k _/s t ) = sin( k _/s t ).

По аналогии с выражением (3) для косинусной функции:

A = 0,9cos( k fs t ) - 0,035 cos(8 k fs t ) + 0,15cos(10 k fs t ) - 0,125 cos(11 k fs t ) + + 0,125cos(13 k fs t ) - 0,15cos(14 k fs t ) + 0,035cos(16 k fs t ) = cos( k fs t ).

Значения амплитуд гармонических составляющих в уравнениях (3) и (4) были определены соответствующими координатами (рис. 2).

С учетом выражений (3) и (4) соотношения (2) примут вид

U ds = 0,707k us A (cos a - sin a ) - 0,707k _us A 1 (cos a + sin a ), U qs = 0,707 k us A 2 (cos a + sin a ) + 0,707 k us A 1 (cos a - sin a ).

Результаты и обсуждение

При номинальных значениях амплитуды и частоты k _us = k f_s = 1 и номинальном движущем моменте, равном m _пд = –0,9 (знак минус указывает на генераторный режим), для синхронной машины был воспроизведен режим прямого подключения к электрической сети.

На рис. 3, а , б , в , г представлены флуктограммы изменения режимных параметров синхронного генератора с постоянными магнитами с учетом влияния высших гармоник напряжения. На первой флуктограмме (рис. 3, а ) изображена кривая электромагнитного момента m _эм = f ( τ ), из которой видно, что после пускового режима ( τ пуска = 0 ÷ 1 200 рад) среднее значение m эм в установившемся режиме равно m эм = 0,9, а флуктуации момента из-за влияния гармоник составляют ∆ _m = ± 14,3 %. Величина частоты вращения ω _r (рис. 3, б ) без колебаний устанавливается на значении ω _r = 1 (строго синхронная частота вращения). Это становится возможным благодаря значительной величине J _об – момента инерции движущихся частей ротора синхронной машины и приводного двигателя.

Величины составляющих токов статора генератора по осям d , q , i d , i q (рис. 3, в , г ) устанавливаются на значениях i _ds = –0,67, i _qs = –0,7.

И наконец, на рис. 3, д представлена флуктограмма изменения активной мощности на зажимах генератора. Из нее видно, что колебания мощности, обусловленные высшими гармониками напряжения, достигают значительных величин и составляют ~ ±40 % от величины установившегося значения, равного p r = –0,89. Это объяснимо, потому что активная мощность на зажимах синхронных машин, записанных в осях, вращающихся со скоростью ротора, определяется по выражению

P — U. i. +U i , pr       ds ds qs qs , т. е. она состоит из произведений составляющих напряжений и токов, кривые которых зависят от гармоник. Если необходимо представить токи в неподвижной системе координат α0, β0, то они примут вид i = L cos a + i sin a, a0 ds              qs,

к = -L sin a + i„. cos a. e0        ds

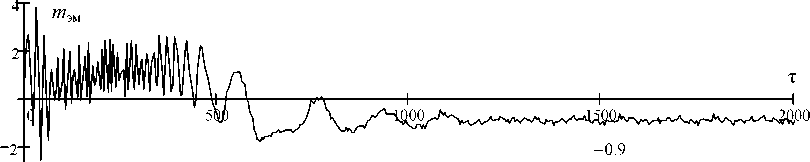
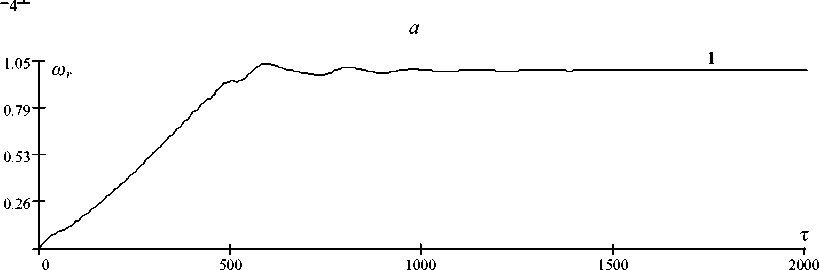
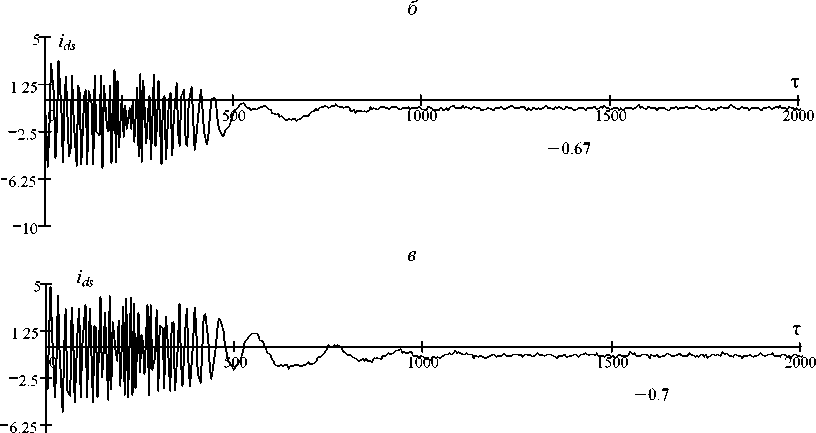
Рис. 3. Флуктограммы изменения режимных параметров синхронного генератора с постоянными магнитами с учетом влияния высших гармонических напряжения Fig. 3. The fluctograms of the change in the operating parameters of the permanent magnet synchronous generator taking into account the effect of higher harmonic voltages

На рис. 4, а , б представлена флуктограмма тока i _{α 0} , полученная по выражению (7) (рис. 4, а ), и развернутое значение этого же тока на интервале 1 500–2 000 рад.

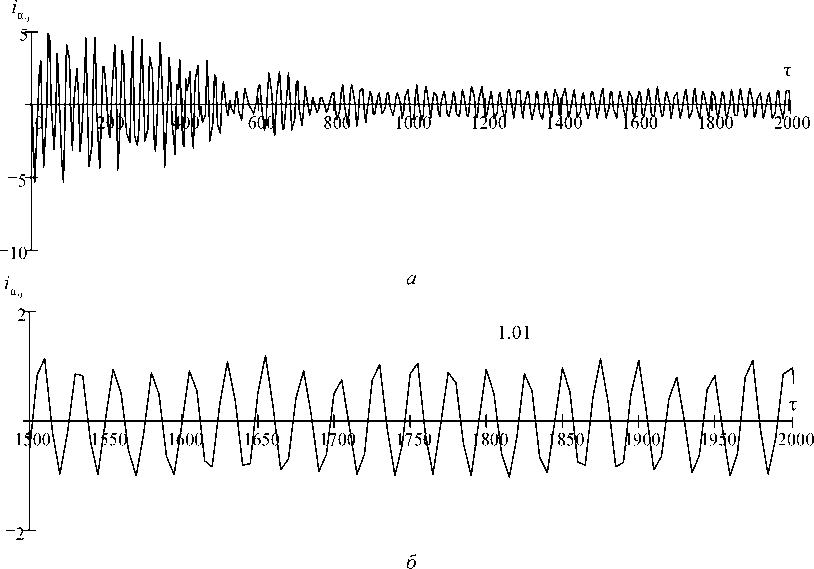
Рис. 4. Флуктограммы изменения тока статора генератора в неподвижной системе координат

Fig. 4. The fluctograms of the stator current of the generator in a fixed coordinate system

Параметры синхронного генератора с постоянными магнитами

Р„ = 1 500 кВт н		U л =690 В	x ad = 0,9135	r s = 0,02
cos ^ = 0,96 (опережающий)		U ф = 400 В	x aq = 0,385	r4, = 0,08
S 1500   1645 кВА		I ф = 1 378 А	x dr = 1,039	r qr = 0,07
cos фп
M н = Р н- = 4 777 Нм		х ds = 1,008	х qr = 0,511	Jоб. = 53 кгм2
Ю б (приведенный к базовой частоте вращения)		x qs = 0, 487	M*} = 1,5	П = 0,95
Базовые величины
S баз =S н =1645кBA	M ба	_ S 6a3 _ 1645 000 “ баз"    314   "	_ 5238,8 Нм
U баз = 2U ф н = 565,7В	Z баз	IL = баз = 0, 26 Ом баз
I баз = 2I ф н =1948,8А	L баз	_ баз _ 0,29 _ о,924 . 10 - 3 Ом.с “ баз 314
“ баз = “ . = 314/с	T j =	J    ■ = 53      4 об S 6a3        1645 ■	3 10 з = 997,5 рад

Так как все индуктивные сопротивления (в о. е.) равны x ^∗ = x [Ом] / Z баз , то и соответствующие им индуктивности (в о. е.) равны L ^∗ = L / L _баз = Lω _баз / Z _баз = x [Ом] / Z _баз . Таким образом, индуктивные сопротивления равны соответствующим значениям индуктивностей: x ^∗ = L ^∗ .

Уравнения решались на базе программы для решения дифференциальных уравнений Мatchad; использовался следующий алгоритм решения:

D ( T , Y ) =

"[ A 12 ( cos ( Y ₆ ) - sin ( Y ) ) -[ A ( cos ( Y ) + sin ( Y ) ) ]]- Y 2 Y 5 - 0,02 ( 4,88 1 ^ - 0,87 - 4,289 Y 3 ) , [ A 12 ( cos ( Y ) + sin ( Y ) ) + [ A ( cos ( Y ) - sin ( Y ) ) ]] + YY - 0,02 ( 5,22 1 2 - 3,906 1 4 ) , - 0,077 1 3 + 0,0703 ( 4,88 1 - 0,87 - 4,289 1 3 ) - 0,1155,

• - 0,137 1 4 + 0,052 ( 5,22 1 2 - 3,0906 1 4 ) ,

  0,001 ( т пд ) - 0,001 [ 1 ( 5,22 Y 2 - 3,906 1 4 ) - 1 2 ( 4,88 1 - 0,87 - 4,289 1 3 ) ] ,

• .                                                   Y 5 ,

A 11 = 0,707 k _us (0,9 sin( k _/s t ) - 0,035 sin(8 k _/s t ) + 0,15 sin(1 0k _/s t ) - 0,125 sin(1 I k _/s t ) +

+ 0,125 sin(13 k _/s t ) - 0,15sin(14 k _/s t ) + 0,035sin(16 k _/s t )),

A 12 = U 3 k us (0,9cos( k fs t ) - 0,035cos(8 k _fs t ) + 0,15cos(10 k _fs t ) - 0,125cos(11 k _fs t ) +

+ 0,125cos(13 k fs t ) - 0,15cos(14 k fs t ) + 0,035cos(16 k fs t )),

Y 1 =v ds ; Y 2 =v ,_s ; Y 3 =v dr ; Y =^ _qr ; Y 5 =® r ; Y 6 =« •

Y =

,

Исследования проведены для режима м _пд = - 0,8 при k us = k fs = 1.

Как было указано выше, флуктограммы, представленные на рис. 3 и 4, отражают номинальный режим работы синхронной машины с постоянными магнитами при номинальных значениях амплитуды и частоты подводимого к статорной обмотке напряжения.

Структура уравнений позволяет исследовать и другие режимы частотного управления, подставляя в эти уравнения другие значения k _us = k f_s (меньше единицы). Кроме того, данная структура позволяет также воспроизводить любой состав гармонических составляющих инвертора напряжения преобразователя частоты (рис. 1). Указанные исследования необходимы, во-первых, для выявления влияния гармонических составляющих на режимные параметры синхронного генератора и, во-вторых, что особенно важно, для правильного расчета параметров фильтра Ф (рис. 1).

Заключение

Разработана методика моделирования, позволяющая учесть влияние высших гармонических составляющих напряжения на режимные параметры частотно-управляемой синхронной машины с постоянными магнитами (причем она предоставляет возможность учесть влияние каждой из гармоник на эти параметры).

Данная методика применяется также для расчета и настройки параметров фильтра (при необходимости его применения).