МЕТОДИКА ИССЛЕДОВАНИЯ ВНУТРЕННЕГО ТРЕНИЯ В РЕЖИМЕ СВОБОДНО ЗАТУХАЮЩЕГО КОЛЕБАТЕЛЬНОГО ПРОЦЕССА (ЧАСТЬ 1)

В работе [1] было представлено устройство для исследования локальных диссипативных процессов (внутреннего трения) в твердых материалах различной химической природы, строения и структуры. Внутренним трением называется процесс необратимого рассеяния в объеме исследуемой системы части энергии внешнего силового механического воздействия, деформирующего эту систему.

Данное устройство, позволяющее исследовать реакцию всех элементов образца материала в динамическом режиме свободно затухающего колебательного процесса, возбуждаемого в исследуемой системе (материале), представляет собой маятниковую конструкцию как горизонтального, так и вертикального исполнения.

Изучение многих физико-механических характеристик в различных по химической природе, строению и структуре материалах основано на исследовании параметров переходных процессов от одного равновесного или неравновесного состояния к другому равновесному состоянию. Динамические характеристики этих переходных процессов оцениваются по коэффициентам переходных функций, представляющих собой реакцию системы как на изменения внутри самой системы, так и на изменение внешних воздействий на эту систему. По интенсивности изменения параметров переходных функций можно получить определенную информацию о структуре исследуемых систем. Наличие переходных процессов от неравновесного к равновесному состоянию неконсервативной системы приводит к термодинамической необратимости данного процесса и, как следствие внутреннего трения, диссипации в исследуемой системе части энергии внешнего силового воздей-

ствия. Количественной характеристикой диссипации энергии в системе является коэффициент поглощения Ψ , связанный с другими диссипативными характеристиками следующим соотношением:

¥ =

A W

2 πW

= Q -¹ = tg 5 = - , π

где A W и W — величины необратимо рассеянной и подведенной к системе энергии соответственно; Q ¹ — внутреннее трение; д — угол сдвига фазы между внешним воздействием и откликом системы на это воздействие — деформацией ε ; λ — логарифмический декремент затухания колебательного процесса.

В качестве меры внутреннего трения в этом случае может быть использован логарифмический декремент λ затухающего колебательного процесса (рис. 1), что позволяет экспериментально получить температурные зависимости диссипативных потерь (спектры внутреннего трения - = f ( T ) ) и температурные зависимости изменения частоты v = f ( T ) свободного затухающего колебательного процесса, возбужденного в образце исследуемого материала. Логарифмический декремент λ входит в уравнение, описывающее колебательный процесс, в виде

Ф⁽t ) = Ф тах exP - ^в® = ^ max exP

λ

π

где ϕ _max и ϕ ( t ) — амплитудные соответственно максимальное и текущее значения угла закручивания незакрепленного конца исследуемого образца; β — коэффициент затухания; θ – период колебательного процесса; t – время.

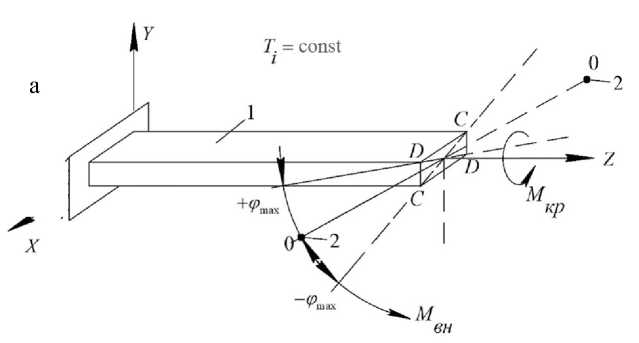
Рис. 1. Схема, описывающая в общих чертах свободно затухающий колебательный процесс, возбуждаемый в исследуемом материале [1].

а — возбуждение колебательного процесса в исследуемом образце прямоугольного поперечного сечения;

б, в, г, д — эпюры затухающего колебательного процесса

б

в

г

д

Из соотношения (2) может быть определен логарифмический декремент колебательного процесса в виде:

X = 1ln

n

ϕ max

Ht ) ,

где n — число колебаний между колебанием, имеющим амплитуду ^ ( t ) , и колебанием, имеющим амплитуду ϕ _max, во временной развертке колебательного процесса (рис. 1, в).

Для каждой температуры T исследования будет иметь место своя временная развертка колебательного процесса (соотношение (2) и свое значение логарифмического декремента λ , а также и свое значение частоты ν колебательного процесса, возбуждаемого в исследуемом образце. Это позволяет получить экспериментальные спектры внутреннего трения X = f ( T ) и температурную зависимость частоты колебательного процесса, возбуждаемого в исследуемом образце v = f ( T ) .

Исследование диссипативных явлений по анализу спектров внутреннего трения в различных по химической природе материалах показывает, что на спектрах внутреннего трения X = f ( T ) может наблюдаться как монотонно возрастающий фон диссипативных потерь (при повышении температуры), так и пики потерь, накладывающиеся на возрастающий фон внутреннего трения (Приложение, рис. П1–П4).

ФОРМУЛИРОВКА ПРОБЛЕМЫ

Анализ экспериментальных спектров внутреннего трения X = f ( T ) показывает, что наиболее "простым" спектром обладают чистые бездефектные монокристаллические металлические материалы, для которых диссипация части энергии внешнего силового воздействия представляется в виде фона внутреннего трения. Этот фон монотонно возрастает при повышении температуры вплоть до температуры фазового перехода T_cr и резко возрастает при T >  T cr. [2-14] (Приложение, рис. П1).

Исследование аналогичных зависимостей для беспримесных, но с различными "структурными дефектами" монокристаллических металлов, по-ликристаллических металлов и сплавов, неорганических кристаллов, стеклообразных неорганических и высокомолекулярных полимерных систем выявляет наличие i-го количества максимумов λi потерь на монотонно возрастающем фоне внутреннего трения X = f (T), и которые располагаются при температурах как твердого агрегатного состояния, так и жидкого агрегатного состояния исследуемых систем. То же самое относится и к высокомолекулярным полимерным системам, находящимся (по определению акад. В.А. Каргина) в твердом и вязкотекучем физических состояниях.

При этом следует отметить, что проявление наличия i -го количества максимумов потерь на монотонно возрастающем фоне внутреннего трения X = f ( T ) , которые располагаются при температурах твердого агрегатного состояния (рис. 2), не позволяет для описания их физико-механических характеристик использовать основную диссипативную характеристику, а именно ее температурное изменение вязкости п = f ( T ) •

Сопоставление спектров X = f ( T ) (рис. 2, а) с соответствующими температурными зависимостями вязкости п = f ( T ) (рис. 2, в) показывает, что наблюдаемые в этих системах пики диссипативных потерь находятся при температурах, при которых экспериментальное значение вязкости η не определено. Оно имеет значительно большее значение, чем значение, соответствующее переходу системы из вязкотекучего структурно-жидкого состояния в неравновесное "замороженное", т.е. твердое состояние [15]. В отличие от вязкостных характеристик исследуемых систем п = f ( T ) , оказывается возможным сопоставление как спектра внутреннего трения X = f ( T ) системы в целом (модель однородного непрерывного сплошного тела), так и сопоставление с локальными диссипативными потерями, проявляемыми на этих спектрах в различных интервалах температур в виде пиков потерь различной интенсивности (модель атомно-молекулярного строения системы), в частности с соответствующими экспериментальными температурными зависимостями изменения частоты v = f ( T ) (рис. 2, б) свободного затухающего колебательного процесса, возбужденного в исследуемой системе.

Как известно, частота колебательного процесса, возбуждаемого в образце исследуемого материала, зависит не только от геометрии (т.е. момента инерции I ) этого образца, но и от модуля упругости (модуля сдвига) материала этого образца, т.е. G « v2. Кроме того, термодинамические расчеты температурной зависимости модуля упругости металлов показывают, что модуль упругости (модуль сдвига G ) при повышении температуры от криогенных значений до температуры кристаллизации Tcr монотонно снижается на 2–4% на ка- ждые 100 градусов повышения температуры (рис. 2, г, штриховая кривая 1) [16], т.е. G = = f (I,v2, T). С учетом того, что момент инерции исследуемого образца изменяется с изменением температуры незначительно, можно принять:

G » f ( v ², T ) .

а

б

в

г

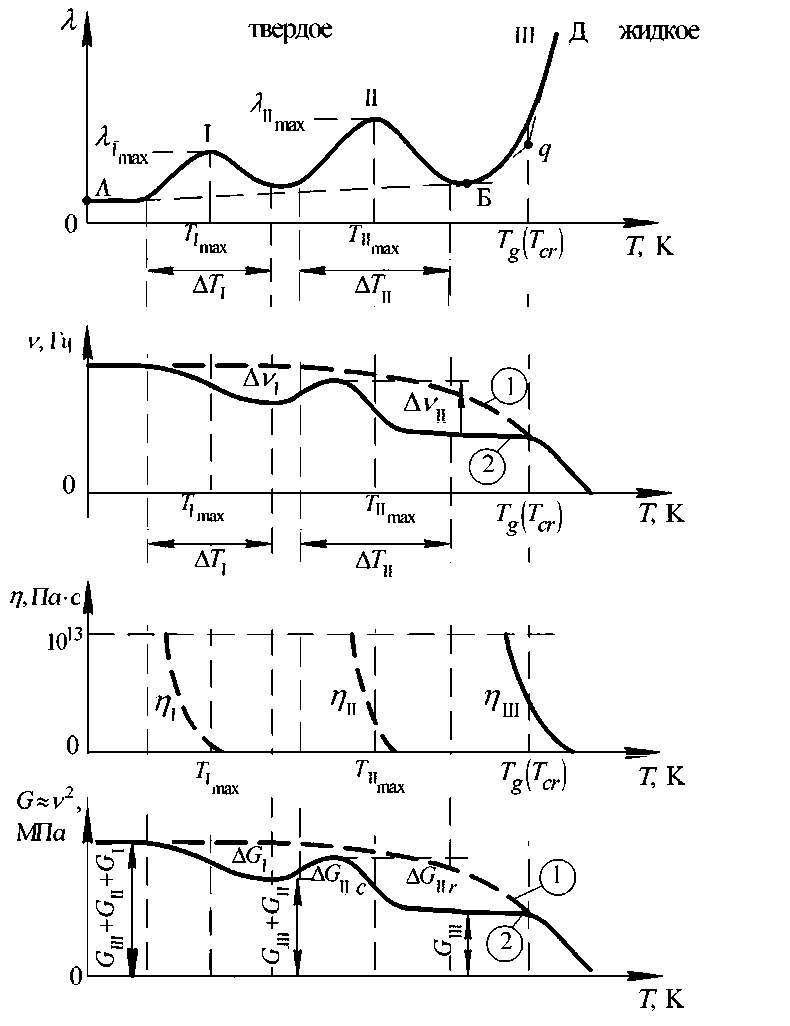
Рис. 2. Схематическое обобщение:

а — спектра внутреннего трения для i -го количества пиков локальных диссипативных потерь;

б — температурной зависимости частоты ν , свободного затухающего колебательного процесса, возбуждаемого в исследуемом образце;

в — температурной зависимости вязкости системы;

г — температурной зависимости модуля сдвига G материала исследуемого образца

В области температур стеклования T_cr или T_g (для аморфных материалов) наблюдается интенсивное уменьшение величины модуля упругости на температурной зависимости G = f ( T ) . При этом для низкомолекулярных материалов значение модуля упругости снижается от величины, соответствующей значению модуля для твердого агрегатного состояния, до величины, соответствующей модулю упругости (сдвига) в жидкости.

Для высокомолекулярных полимерных материалов в области температур T_g (температура стеклования) также наблюдается снижение величины модуля упругости, но не до значения, соответствующего модулю упругости жидкости, а до значения модуля упругости высокоэластичного состояния G_ВЭ , а при дальнейшем повышении температуры до значения вязкотекучей жидкости.

Таким образом, на температурных зависимостях частоты (рис. 2, б) и соответственно модуля G = f ( T ) (рис. 2, г) наблюдается отклонение экспериментальной кривой частоты от ее теоретически рассчитанного значения. Следовательно, на температурной зависимости модуля упругости (сдвига) будет наблюдаться аналогичное отклонение, которое соответствует разности модулей упругости твердого агрегатного и высокоэластического физических состояний полимерной системы.

Дальнейшее повышение температуры до температуры перехода из высокоэластического в вязкотекучее состояние приводит ко второй температурной зоне интенсивного снижения модуля упругости.

Следует отметить, что если температура деструкции T_p полимера ниже температуры перехода в вязкотекучее состояние T g , т.е. ( T p <  T g ), то зависимость G = f ( T ) в этом интервале температур может быть более сложной, чем в случае, когда ( T P >  T g ).

В области твердого агрегатного состояния ( T ≪ ≪ T g ) (рис. 2, а) основным параметром, характеризующим это состояние, является модуль упругости, который в самом общем случае для анизотропных систем может определяться законом Гука, представляемым в виде:

S j = G jkl S kl , ⁽⁴⁾

где σ_ij — компоненты тензора напряжения соответственно, возникающие в исследуемом материале при его деформировании на величину ε_kl ; G_ijkl — компоненты тензора модулей упругости.

В области жидкого агрегатного состояния ( T >  T_g ) (рис. 2, а) или ( T >  T cr. ) основным параметром, характеризующим это состояние (рис. 2, в), является вязкость, которая в самом общем случае может определяться из соотношения Навье – Стокса (обобщенного закона Ньютона) в виде:

^ ij = n i _jk i ^S ki , ⁽⁵⁾

( . ds dA где s - Ui =— = s— , Si — компоненты тен-< kl kl dt dt J kl зора скорости деформации (скорость смещения относительно друг друга структурно-кинетических единиц исследуемого материала); ηijkl — компоненты тензора вязкости.

При стремлении компонентов тензора вязкости n i _jkl ^ да скорость смещения относительно друг друга структурно-кинетических единиц исследуемого материала стремится к е ; kl ^ 0, т.е. подвижность структурных элементов в данной системе прекращается.

Таким образом, при температурах ( T <  T_g ) или ( T <  T_cr ), т.е. в области твердого агрегатного состояния при повышении температуры от 0 до T_g или T_cr теоретически должен наблюдаться возрастающий фон потерь (рис. 2, а, штриховая линия) и не наблюдаться никаких пиков потерь.

Однако экспериментальные данные показывают, что такое диссипативное поведение исследуемых систем характерно только для бездефектных монокристаллических металлов (Приложение, рис. ПI, кривая 1). Для всех других материалов в этом интервале температур может наблюдаться от 1–2 до 10–12 локальных по температурному интервалу своего проявления пиков диссипативных потерь [12–14, 17].

Из этого следует, что для описания локальных диссипативных процессов, проявляющихся в данных интервалах температур, использование вязкости (рис. 2, в) и модуля упругости E (или модуля сдвига G ) всей системы, рассматриваемой с модельных представлений сплошной однокомпонентной, бездефектной изотропной среды, не представляется возможным. В то же время классическая теория распространения упругой волны в сплошных твердых и вязких теплопроводных и сжимаемых средах, в первом приближении, связывает коэффициент поглощения (т.е. диссипативную характеристику) именно с вязкостными характеристиками (объемной и сдвиговой вязкостью), теплоемкостью ( C_V и C_P ), теплопроводностью [18, 19].

Возникает вопрос о том, какие же диссипативные и упругие характеристики необходимо использовать при температурах ( T <  T g ) или ( T <  T cr ), т.е. в области твердого агрегатного состояния, для описания локальных диссипативных процессов, наблюдаемых на спектрах внутреннего трения к = f ( T ) , для систем, которые не являются однокомпонентными, бездефектными и изотропными.

Прежде чем проводить теоретический анализ природы наблюдаемых на полученных спектрах к = f ( T ) различных локальных диссипативных процессов, определим погрешность измерений данного устройства.

О ТОЧНОСТИ ИЗМЕРЕНИЙ

Метод внутреннего трения (ВТ) в режиме свободно затухающего колебательного процесса является высокочувствительным методом, что подтверждается экспериментальными исследованиями к = f ( T ) и v = f ( T ) структурных перестроек при фазовых переходах в сегнетоэлектрических кристаллических системах [7]. Оценка чувствительности метода в самом общем виде может быть проведена на базе полученных пиков диссипативных потерь, представленных на спектре Q - 1 = f ( T ) для титаната бария BaTiO₃ (рис. 3).

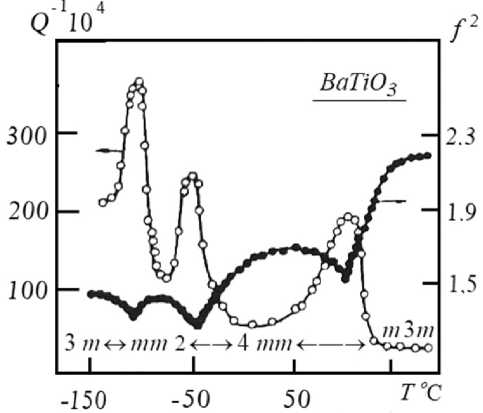
Рис. 3. Спектр внутреннего трения Q ¹ = f ( T ) и температурная зависимость частоты свободно затухающего процесса f ² = f ( T ) для BaTiO₃ (по данным работы [7])

Полученное экспериментальное значение для пиков диссипативных потерь на спектре Q—1 = f (T) (рис. 3) лежит в интервале значений Q- = tg 5 = — «10-2 + 10-3, поэтому, учитывая об-π щее соотношение для характеристики внутреннего трения в виде [8]:

.      Im G *(ito)   G "(to)   £неупр к = п--^—- = —« ——,

Re G (i to )    G '(i to )     в упр

где G * (i a ), G ' ( to ), G "( to ) — комплексный модуль сдвига, модуль сдвига и модуль потерь соответственно; ε_неупр , ε_упр — неупругая и упругая компоненты деформации образца.

Амплитуда упругой деформации образца при его закручивании относительно продольной оси на угол ф^ = 1 ° (рис. 1, а) составляет Y_ynp ~ ^е у _пр = 10 ^- 5 ^ 10 " 6 [1], следовательно, из соотношения ⁽⁶⁾ следует Y _m ax ~ 8_Н еу _П р ~ ¹⁰ - 2 • 10 - ⁵ » ¹0 - 7 . Полученное значение чувствительности устройства ( ^£ _неупр ~ 10 - 7 ) позволяет фиксировать неупругие деформации кристаллической решетки, связанные с подвижностью атомов и молекул при их реакции на внешнее воздействие.

На примере полиметилметакрилата (ПММА) [12]; [20, с. 43] рассмотрен режим амплитуднонезависимого внутреннего трения (АНВТ) при различных амплитудных значениях угла ϕ _max закручивания образца и получаемых при этом величин относительной деформации γ _max и величины напряжений σ _ij , возникающих при этом в граничных плоскостях исследуемого образца:

' ф _m ax = 1 ° ;      Y max = 1.5 "Ю - ³;

^<_ Ф max = 0.5 ° ; Y max = 7.5 . 10 - 4 ;

^   = 1.5 - 10⁶Па;

ij _max

^   = 7.5 - 10⁵Па.

ij max

Кроме рассмотренных величин погрешности и чувствительности данного метода, следует также провести анализ величины погрешности измерений ВТ, вызванной перепадом температур AT на внутренних и внешних границах исследуемого образца, т.е. по поперечному сечению образца, зафиксированного в зажимах колебательной системы устройства. Данный анализ был проведен на сегнетоэлектриках для исследований внутреннего трения фазового механизма диссипативных потерь [7]. При этом квадратное поперечное сечение (с целью упрощения расчетов) заменялось в расчетах теоретическим сечением в виде окружности с радиусом r = 1.5 мм. Наличие перепада температур AT по радиусу поперечного сечения образца должно приводить к тому, что пики потерь на спектре X = f (T), связанные с фазовыми структурными переходами на внешних слоях образца, будут происходить раньше, чем фазовые превращения на внутренних областях. Это может привести к расширению температурного интервала проявления пика диссипативных потерь на спектре, что, в свою очередь, приведет к расширению непрерывного спектра времен релаксации H (т) этого процесса. Перепад температур определялся на примере керамики (рис. 3) по соотношению:

1 Т 2^г

A T «--« 0.5 ° C,

2 χ

где I / = d- I , х = 7 - 10 - 3

I     dt )

см2 с

— температу-

К ропроводность керамики BaTiO3, T = 20 --- — мин скорость изменения температуры окружающей среды.

Учитывая, что температурный интервал пика диссипативных потерь на спектре внутреннего трения (рис. 3) при переходе системы BaTiO3 из тетраэдрической (4mm) в тригональную (m3m) фазу составляет ~100 °C, полученный перепад температур AT практически не оказывает влияния на весь температурный интервал структурного фазового перехода II рода, т.к. T ≫ ΔT.

Однако полученный перепад

AT ® 0.5 °C может вызвать появление гих деформаций εТ , возникающих в следуемого образца. Оценка влияния температур термоупру-объеме ис- возникших

термоупругих деформаций ε_Т на максимальное значение деформации образца у max ~ 10 ^{- 3} при его закручивании на угол ф _тах = 1 ° в момент времени t ₀ (рис. 1) может быть определена по соотношению:

£_Т »— a_T A T « 6 - 10 ^{- 7}, (9)

где a_T = 2.5 - 10 " ⁶ ^ град " ¹ ] — величина коэффициента линейного расширения BaTiO₃ для интервала температур + 50 -г + 200 ° С.

Полученное значение термоупругих деформаций εТ вследствие малости своего значения при фазовом переходе (4mm)^(m3m) практически на четыре порядка меньше начального амплитудного значения закручивания исследуемого образ- ца, что не приводит к заметному влиянию термоупругих деформаций на весь колебательный процесс.

ЗАДАЧИ И ЦЕЛИ ИССЛЕДОВАНИЯ

Целью данной работы является описание методик расчетов физико-механических и физикохимических характеристик различных диссипативных процессов, получаемых на устройстве [1] и проявляемых на спектрах внутреннего трения X = f ( T ) и на температурных зависимостях частоты v = f ( T ) свободного затухающего колебательного процесса, возбуждаемого в образцах исследуемых материалов различной химической природы, строения и структуры в разных температурных интервалах (от –150 до +500 °С).

Для достижения поставленной цели представлены экспериментальные результаты X = f ( T ) и v = f ( T ) для различных по химической природе материалов, рассмотрены основные феноменологические модельные представления, на базе которых проводится расчет различных физикомеханических и физико-химических характеристик локальных по температуре диссипативных процессов, которые могут иметь различные механизмы внутреннего трения (гистерезисный, фазовый, релаксационный).

ЭКСПЕРИМЕНТАЛЬНЫЕ СПЕКТРЫ ВНУТРЕННЕГО ТРЕНИЯ λ = f ( T ) И ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ ЧАСТОТЫ ν = f ( T ) ДЛЯ РАЗЛИЧНЫХ ПО ХИМИЧЕСКОЙ ПРИРОДЕ МАТЕРИАЛОВ

В Приложении на рис. П1–П4 представлены в качестве примера экспериментальные результаты, полученные как различными авторами, так и авторами данной работы.

Следует отметить, что исследование спектров внутреннего трения весьма бурно проводилось в середине и конце XX в., особенно на металлах и различных сплавах [2–8, 17].

Однако конструктивная простота устройств, реализующих метод внутреннего трения, могла привести к результатам, которые существенно различались.

Например, фиксация параметров затухающего крутильного колебательного процесса осуществлялась с помощью "светового зайчика", а период колебаний — с помощью обычного механического секундомера. Все это вносило большую субъективную погрешность получаемых результатов.

Усложнение конструкции устройств и компьютеризация в получении и обработке эксперимен- тальных результатов в XXI в. позволили получать достоверные спектры к = f (T) особенно в области низких температур, где обнаруживаются пики диссипативных потерь малой интенсивности, которые значительно ниже интенсивности диссипативных потерь, наблюдаемых в области температур стеклования Tg (аморфные материалы) или в области кристаллизации Tcr (кристаллические материалы).

Учитывая, что процессы, наблюдаемые в областях температуры стеклования T_g , имеют релаксационный механизм внутреннего трения, вектор исследований сместился только в направлении этого α -процесса в режиме вынужденных динамических колебательных процессов, частота которых может варьироваться в диапазоне от 10^–2 до 10³ Гц. Однако именно вынужденный процесс смещения структурно-кинетических единиц исследуемых систем (материалов) не позволил данными методами динамического механического анализа (ДМА) проводить исследования тонких спектров внутреннего трения, на которых каждая структурно-кинетическая подсистема резонансно (на собственной частоте) и в определенном температурном интервале может проявиться в виде низкоинтенсивных локальных диссипативных процессов.

При этом следует особенно отметить пионерские работы по исследованиям тонких спектров внутреннего трения в сегнетоэластиках и сегнето-керамиках, полученных в режиме свободно затухающего колебательного процесса, проф. С.А. Гриднева [7].

Только в последние годы исследованиями проф. Г.М. Бартенева был восстановлен интерес к решению основной задачи физико-химической механики, которая была сформулирована акад. П.А. Ребиндером и чл.-корр. М.В. Волькенштей-ном в виде: "химическая природа, строение, структура – физико-механические и физико-химические характеристики – синтез материалов с заданными свойствами" [10, 11].

ЗАКЛЮЧЕНИЕ

Наличие диссипативных процессов различной интенсивности, проявляемых в виде пиков потерь на спектрах внутреннего трения в различных температурных интервалах, и соответствующего им аномального изменения частоты свободно затухающего колебательного процесса, позволяют разработать метод и методику теоретического анализа этих процессов и оценить погрешность этих исследований.

Данная статья является вступительной в работе, состоящей из трех частей, которые будут опубликованы позже в этом же журнале.

ПРИЛОЖЕНИЕ

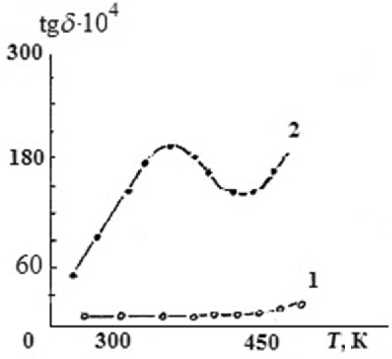
Рис. П1. Кривые коэффициента поглощения Ψ = tg δ в функции от температуры для монокристаллического (1) и поликристаллического (2) бесдислокационного олова (99.99% Sn), полученные при частоте ν = 3·10² Гц [2, 17]

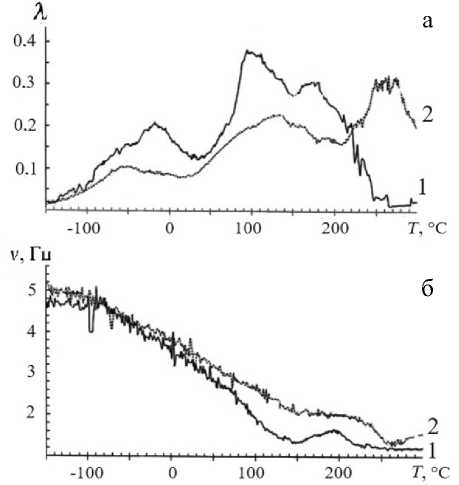
Рис. П2. Спектры внутреннего трения (а) и температурные зависимости частоты (б) образцов хитозана в солевой (1) и основной (2) формах [21]

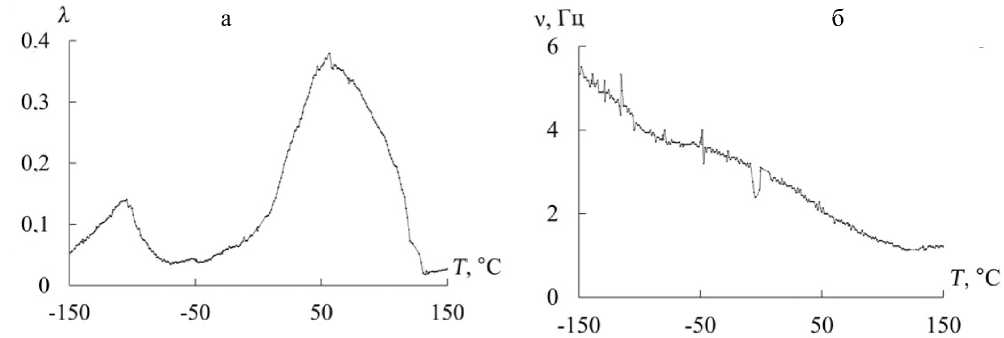
Рис. П3. Спектр внутреннего трения (а) и температурная зависимость частоты (б) образцов полиэтилена [14]

1.2

<0

0.8

0.6

о Чо3

320 400 480 560 640 720 800 T/C

а

б

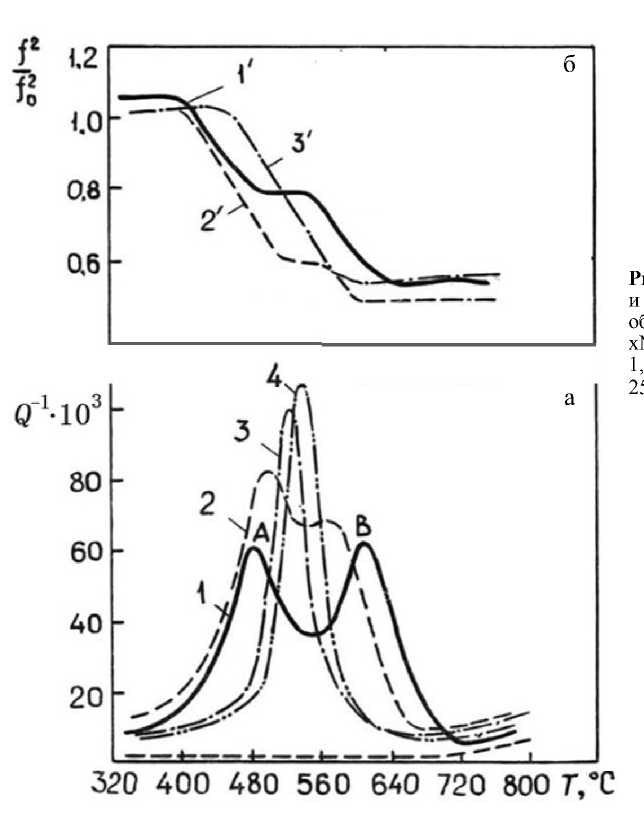
Рис. П4. Спектр внутреннего трения (а) и температурная зависимость частоты (б) образцов ликвирующих стекол xNa 2 O·25B 2 O 3 ·(75–x)SiO 2 [8].

1, 1` — 3%; 2, 2` — 6%; 3, 3` — 10%; 4 — 25% Na 2 O мол%