МЕТОДИКА ИССЛЕДОВАНИЯ ВНУТРЕННЕГО ТРЕНИЯ В РЕЖИМЕ СВОБОДНО ЗАТУХАЮЩЕГО КОЛЕБАТЕЛЬНОГО ПРОЦЕССА. Ч. 2. ТЕОРЕТИЧЕСКИЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ РЕЗУЛЬТАТОВ

Анализ спектров внутреннего трения к = f ( T ) и температурных зависимостей частоты v = f ( T ) свободного затухающего колебательного процесса, возбуждаемого в исследуемых образцах различной химической природы, строения и структуры [1, рис. 2] в широком температурном интервале показывает, что внутреннее трение как диссипативный процесс по физической сути представляет собой гораздо более глубокое явление, которое не может быть полностью описано в рамках модельных представлений однородного сплошного тела.

Эта глубина обуславливается тем, что спектры к = f ( T ) для одного какого-либо материала (или конденсированной системы) в широком температурном интервале ( 5 К <  T <  Т дестр ) представляют собой целый набор локальных по температурным интервалам диссипативных процессов различной интенсивности.

Каждый локальный диссипативный процесс на спектре к = f ( T ) проявляется в виде пика потерь различной интенсивности, а на температурной зависимости частоты v = f ( T ) в виде аномального поведения этой зависимости.

Таким образом, реакция исследуемой системы на внешнее деформирующее воздействие требует рассмотрения процессов диссипации с модельных представлений атомно-молекулярного строения исследуемых систем. В этом случае вся исследуе- мая система представляет собой совокупность структурно-кинетических подсистем, квазинезави-симо реагирующих на внешнее воздействие. Это воздействие одновременно выводит все структурные элементы (атомно-молекулярные образования или структурно-кинетические подсистемы) из положения механического и термодинамического равновесия.

Реакция каждой структурно-кинетической подсистемы при одной температуре, равной для всех, будет различной: от упругой (гуковской) до неупругой (максвелловской), что и отражается на зависимостях к = f ( T ) и v = f ( T ) [2].

Метод внутреннего трения, рассматриваемый в динамическом режиме свободного затухающего колебательного процесса, возбуждаемого в однородной непрерывной сплошной среде, и упруго реагирующей на внешнее воздействие в изотермических условиях ( T = const), базируется на основном уравнении движения:

p^ i" ^ j , (1)

где ρ — плотность среды; ϕ_i — угол закручивания образца; σ_ij — компоненты тензора напряжения соответственно, возникающие в исследуемом материале при его деформировании на величину ε kl .

Решение уравнения (1) представляется в виде [2]:

(а ф, I         i -a ф(z , t )

J=S Bi I dz

( t - t0 ) τi

d t ,

где z — координата поперечного сечения образца; Bi — положительная постоянная, удовлетво-n ряющая условию S Bi = G, где G — модуль сдвига i=1

всей системы, состоящей из n числа структурнокинетических подсистем; t — текущее время колебательного процесса; t ₀ — время приложения внешнего скручивающего момента M_вн ; τ_i — время релаксации i -й структурно-кинетической подсистемы.

Использование преобразования Лапласа – Карсона [3] позволяет получить решение, которое при t >  1 0 описывает процесс затухания крутильных колебаний исследуемого образца относительно равновесного значения угла ф = 0 [1, рис. 1, в].

В этом случае определяется логарифмический декремент основной (для определенной температуры) гармоники колебательного процесса. Изменение температуры ведет к изменению основной гармоники, т.е. к изменению преобладающей в данном температурном интервале, доминирующей по диссипативной способности, структурно-кинетической подсистемы ( i -й подсистемы). Логарифмический декремент колебательного процесса, возбужденного в исследуемой системе, состоящей из n числа структурно-кинетических подсистем, определится в виде:

X =

Первые два слагаемых в соотношении (3) связаны с фоном внутреннего трения спектра X = f ( T ) , а третий член этого соотношения — с пиками потерь, налагаемыми на фон. В модельном представлении соотношение (3) может быть представлено в виде обобщенной модели Максвелла с вырождающимися при изменении температуры ветвями [2], а третье слагаемое в соотношении (3) может быть записано в модельном представлении стандартного линейного тела [5]:

λ i

= 2 X i

ωτi

max

1 + T 2 т 2

= п <

а о а1

( Gor J

+

( R A

_B^_ I

( G t 2 J

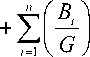
_v 1 + T ^Ti^

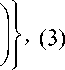
где ω — круговая (циклическая) частота; τ ₁, τ ₂ , ..., τ_i — времена релаксации для каждой i -й структурно-кинетической подсистемы; B ₁ , B ₂ , ..., B_i — положительные постоянные, имеющие размерность модуля сдвига [Н/м²] для каждой структурно-кинетической подсистемы.

Согласно феноменологическим модельным представлениям Максвелла [4] и основным положениями теории внутреннего трения [5–10], связь между возрастающим по интенсивности фоном внутреннего трения tg δ , логарифмическим декрементом λ колебательного процесса, круговой частотой ω этого процесса и временем релаксации τ определяется соотношением

X = — tg 5 = — . (4)

ωτ

где λ_i — максимальное значение логарифмического декремента на спектре внутреннего трения X = f ( T ) для каждого пика диссипативных потерь [1, рис. 2, а].

Время релаксации для элементарной модели Максвелла связано с физико-механическими характеристиками исследуемой системы и зависит от температуры:

ηU

^T = G = ^T oexP RT, (6)

где G — модуль упругости (сдвига); τ ₀ — пред-экспоненциальный коэффициент; U — энергия активации процесса; T — температура; R — универсальная газовая постоянная.

В этом случае фон внутреннего трения (соотношение (3)) и пик диссипативных потерь на спектре X = f ( T ) (соотношение (5)) будут зависеть от температуры.

Соотношения (1)–(6) могут качественно представить весь спектр внутреннего трения в его температурно-частотной зависимости и применимы как для аморфных стеклообразных и кристаллических, так и для жидких (стеклообразующих и кристаллизующихся) систем.

Кроме этих положений следует отметить тот факт, что и модуль сдвига G является хотя и слабой, но зависящей от температуры характеристикой, т.е. G = f ( T ) .

Исследования внутреннего трения монокристаллических систем [1, рис. П1] показывают: на спектрах внутреннего трения наблюдается возрастающий фон и монотонный спад модуля сдвига, который по теоретическим расчетам составляет ® 2 ^ 4% на каждые 100 градусов температуры [11].

Спад модуля сдвига интенсифицируется в области температур плавления (кристаллизации) для кристаллических систем или в области температуры стеклования для аморфных систем.

Однако для этих же кристаллических систем, находящихся в поликристаллическом структурном состоянии, на фон внутреннего трения при температурах ниже, чем температура кристаллизации ( T <  T c _r ), накладывается возникший пик диссипативных потерь (одна из компонент третьего слагаемого соотношения (3).

Следует отметить, что и на температурной зависимости модуля сдвига в этом же интервале температур начинает проявляться аномальное отклонение значений модуля G от плавно монотонной температурной зависимости G = f ( T ) .

Эти изменения в спектрах к = f ( T ) и зависимостях G = f ( T ) произошли в результате изменения внутренней структуры соответствующих подсистем, построенных из тех же структурных элементов, как и соответствующие монокристаллы.

Исследования зависимостей для аморфных систем также выявляют аналогичные эффекты [1, рис. П2–П4].

АНАЛИЗ СОВОКУПНОГО ДЕЙСТВИЯ СТРУКТУРНО-КИНЕТИЧЕСКИХ СОСТАВЛЯЮЩИХ ПОДСИСТЕМ

Все рассмотренное выше дает основание при глубоком теоретическом анализе реакции исследуемых материалов (систем) в динамических режимах свободно затухающих колебательных процессов, возбуждаемых в них, учитывать не только температуру и частоту, но и атомно-молекулярное строение исследуемой системы.

При этом сама исследуемая система представляется в виде совокупности структурнокинетических (атомно-молекулярных) подсистем с разными физико-механическими и физикохимическими характеристиками, квазинезависимо реагирующих на одинаковые внешние воздействия, выводящие все элементы этих подсистем из состояния механического и термодинамического равновесия [12].

Рассмотрим случай, когда исследуемый образец материала состоит из трех структурных подсистем (например, из звеньев цепи макромолекулы полимера — подсистема I, из сегментов этой цепи — подсистема II и надмолекулярных образований — подсистема III).

Дифференциальное уравнение в модельном представлении Максвелла для данной системы будет иметь вид:

⁰ + G о + — о + — о = ( G i + G _п + G _m) ^Y, (7) η I      η II      η III

d σ

где о = — — скорость изменения напряжения d t

dγ на всей системе; у = — — скорость изменения dt деформации сдвига; σ — напряжение на образце; ηI , ηII и ηIII — диссипативные (вязкостные) параметры подсистем I, II и III; GI , GII и GIII — модули сдвига подсистем I, II и III.

В данном случае реакцией подсистемы, образующей фон внутреннего трения на спектре, можно пренебречь, приняв ее чисто упругой гуковской реакцией, лишенной неупругих свойств. Следует отметить, что это допущение является лишь качественным, т.к. величина фона имеет определенное значение даже при криогенных температурах, что свидетельствует о том, что фон потерь на спектре также является диссипативным процессом проявления неупругости, хотя и с бесконечно большим временем релаксации, что будет рассмотрено ниже.

Решением уравнения (7) является соотношение [2]:

^О ( t ) = ^G I Y max exp

—

— + Gи Y TIJ

+ ^G III Y max exP

—

t

^T II I J

,

max exp

t

—

τ

" +

II J

где t — время, с [1, рис. 1].

В этом случае имеет место три времени релаксации, т.е. каждая структурно-кинетическая подсистема характеризуется своими релаксационными характеристиками:

T = nr ■

I    _{G I}

η II             η III

^T II =      ■ ^T iii =

G II             G III

.

Соотношение (8) может быть преобразовано

к виду:

G (t) r = ^(H = G

γ max

+ G II exp

exp

—G11+

I n )

<      ^

—--L t | + GIII exp l Пii )

— G ¹- 1 | , l   n III   )

где G ( t ) r — релаксирующий модуль сдвига.

Учитывая, что каждая элементарная феноменологическая модель Максвелла характеризуется своей функцией релаксации, имеющей в статическом изотермическом режиме внешнего воздействия вид

T i ( t ) = exp

Г t)--I = exp

I TJ

—

V n

GM I ,

можно принять, что общий процесс релаксации всей трехкомпонентной системы будет определяться соотношением

Ti( t ) = Ti (t) + Tii (t) + Tiii (t),           (12)

а релаксирующий модуль:

G ( t ) _r = G i T i ( t ) + G ii T ii ( t ) + G „I T iii (t ) .       (13)

Следует отметить, что время релаксации τ _I , τ _II и τ _III каждой структурно-кинетической подсистемы зависит от температуры исследования; поэтому, учитывая структурное различие I, II и III подсистем, каждая подсистема будет характеризоваться своей температурной зависимостью времени релаксации T i = f ( T ) , а следовательно, и своими физико-механическими и физико-химическими характеристиками (энергия активации U_i ; вид функции релаксации T i ( t ) ; время релаксации T i ; предэкспоненциальный коэффициент τ ₀ и т.д., соотношения (6) и (11).

В этом случае при одних температурах исследований (например, температуре T [1, рис. 2]) max время релаксации одной структурно-кинетической подсистемы (например, подсистемы I) может быть значительно меньше, чем время релаксации второй структурно-кинетической подсистемы при той же температуре T (качественно температурная max зависимость времени релаксации согласуется с температурной зависимостью вязкости той или иной структурной подсистемы [1, рис. 2, в]), т.е.:

τ _{I Ti} ≪ τ _{II Ti} ≪ τ _{III Ti} .                  (14)

На рис. 1, а, представлены 4 модели исследуемой системы для интервалов температур:

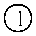
— T <  T

I max

T     T I max ;

(4)_ т ~т

Vv T ~ T iii

^; max

max

и их трансформации рис. 1, б, в; [1, рис. 2].

В Приложении на рис. П дана общая схема.

В области температуры T <  T I спектра Л = f ( T ) [1, рис. 2, а] имеет место фон внутреннего трения, в образовании которого принимают упругое участие все три структурно-кинетические подсистемы: I, II, III.

Все диссипативные (неупругие) процессы в этих подсистемах пренебрежительно малы, поэтому эти подсистемы будут характеризоваться значением "замороженной" вязкости ηi* (обозна ченной на рис. 1 и 2 символом ).

В области температуры T ~ T I     спектра

Л = f ( T ) начинает проявляться пик I диссипативных потерь [1, рис. 2, а], что свидетельствует о проявлении неупругой локальной подвижности элементов I структурно-кинетической подсистемы, т.е. величина вязкости этой подсистемы η _I (обозначенной на рис. 1 символом без окружности, т. е. ) становится меньше "замороженно- * го значения n I <  n i •

В этом случае модель трансформируется из положения 1 (рис. 1, а) в положение 2 (рис. 1, а).

Вследствие того, что оставшиеся "замороженные" вязкости ηI*I и ηI*II не оказывают влияния на диссипативный процесс I в области температур T ~ T , они могут быть опущены из модельного Imax представления всей системы (фиг. 2- на рис. 1, б), а упругие элементы подсистем II и III могут быть представлены общим упругим элементом (GII + GIII) (фиг. (2= на рис. 1, в), а вся модель переходит в модель стандартного линейного тела (фиг. 2= на рис. 1, в).

Аналогично осуществляется и преобразование модели при температурах T >  T I (фиг. ((3 и (4(( на рис. 1). Однако при T « T значение вязкости

II max

П I стремится к нулю, т.е. n I ^ 0 и упругая компонента G I ^ 0, поэтому ветвь модели п I — G I утрачивается (рис. 1, а, фиг. 3 ).

В области температур T « T III из общей модели остается лишь модель с вязкостью η _III и модулем сдвига G _III , т.е. вся модель трансформируется в простую модель Максвелла (рис. 1, а, фиг. 4 ).

В области температуры T первая структур-max но-кинетическая подсистема проявляет диссипативные вязкостные характеристики вследствие того, что nI < 1013 Пз [1, рис. 2, в].

В первом приближении элементарная модель Максвелла (II подсистема) вырождается в упругую (квазиупругую) гуковскую модель, вследствие чего обобщенная, состоящая из двух максвелловских ветвей модель [рис. 1] преобразуется в феноменологическую модель стандартного линейного тела с одним временем релаксации [2, 12–15]:

а

б

в

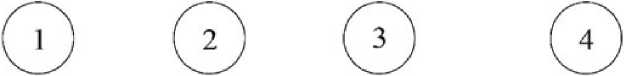
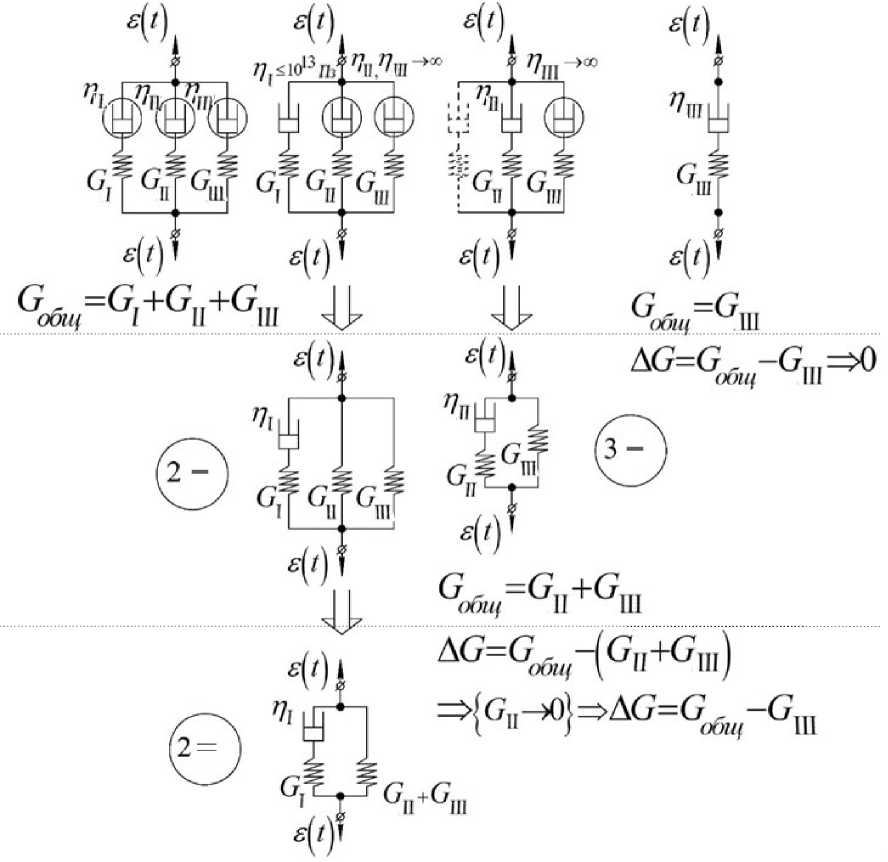
Рис. 1. Схематическое обобщение и теоретический анализ соответствующих феноменологических модельных представлений для каждого из 4 температурных интервалов спектра Л = f ( T ) из [1, рис. 2]

• — + G- — = ( GI + GII) Y + GG Y = ηI

• = ст + — = (GI + GII)у + — /•(15)

ττ

В динамическом режиме внешнего воздействия в виде

Y (t ) = Ymax eiBt(16)

дифференциальное уравнение модели стандартного линейного тела (соотношение (15)) представляется в виде

G

7 + —^L 7 = η _I

(GI + GII) ito +

' G i G„

I nI

γ max

i ωt e

•

σ

= 7 + — = τI

⁽ G I ⁺ G II ) ^{i to +} — ^{Y T} I J

^{i ω t} (17) max .

Решением уравнения (17) является уравнение

Л = 2 A      ^toT I ₂ .

max 1 + ю 2 т 2

МЕХАНИЗМ ВНУТРЕННЕГО ТРЕНИЯ

Исследование температурных и частотных зависимостей внутреннего трения и температурных зависимостей частоты свободно затухающего колебательного процесса, возбуждаемого в различных по химической природе, строению и структуре материалах (систем), позволяет представить эти результаты в виде некоторой обобщенной кривой диссипативных потерь в интервале температур от ~10 К до ~700 К — Л = f ( T ) [1, рис. 2, а] и обобщенной кривой температурной зависимости частоты v = f ( T ) [1, рис. 2, б].

На спектрах Л = f ( T ) наблюдается непрерывный, слабо и монотонно возрастающий (или постоянный по величине) при повышении температуры до температуры изменения агрегатного состояния системы ( T ≪ T g ) [1, рис. 2, а] участок АБ (штриховая линия) и участок БД (сплошная линия) экспоненциально возрастающего фона внутреннего трения при температурах T >  T g .

На фон диссипативных потерь при T <  T g в различных температурных участках спектра Л = f ( T ) накладываются пики диссипативных потерь λ [1, рис. 2, а].

i max

Как было отмечено выше, пики диссипативных потерь обусловлены проявлениями (при изменении температуры) возрастающей возможности локальной подвижности элементов, образующих различные структурно-кинетические подсистемы, квазинезависимо и неодинаковым образом реагирующие на одинаковые внешние воздействия, и образующих в совокупности всю атомномолекулярную структуру всей исследуемой системы.

Таким образом, эти пики диссипативных потерь имеют различное структурно-кинетическое

происхождение, различный механизм внутреннего трения и различную интенсивность.

Кроме того, на температурной зависимости частоты v = f ( T ) свободного затухающего колебательного процесса [1, рис. 2, б] наблюдаются аномальности этих зависимостей, проявляющиеся в температурных интервалах пиков диссипативных потерь Л на спектре Л = f ( T ) [1, рис. 2, а].

Эти аномальности заключены в отклонениях (в той или иной степени) от теоретической кривой ^V meop = ^f ( ^T ) (штриховая линия (Г) [1, рис. 2, б^]), рассчитанной по температурной зависимости модуля упругости G meop = f ( T ) [1, рис. 2, г] (штриховая линия).

Расчет теоретической зависимости v = f ( T ) проведен в соответствии с положением физики твердого тела [11], согласно которому модуль упругости исследуемой системы должен уменьшаться на (2÷4)% при увеличении температуры на 100 град. до температуры перехода системы из твердого в жидкое агрегатное состояние, т.е. в интервале температур ~10 К <  T <  T_g зависимость G = f ( T ) предполагается линейной.

Для динамических режимов исследования различных материалов, находящихся в твердом агрегатном состоянии, имеется связь между модулем упругости материала и частотой колебательного процесса, возбуждаемого в исследуемом образце в виде [16]:

G = f ( I , v , T ) ^ G « ( Iv ² ) T , (19)

где I — момент инерции исследуемого образца.

Таким образом, модуль упругости (сдвига) зависит не только от температуры, но и от частоты (при условии I = const), т.е.

A G ( T , v ) = A v ² ( T )           (20)

температурное изменение частоты ν позволяет определить и температурное изменение модуля сдвига, что теоретически может быть представлено в виде штриховых линий 1 зависимостей на [1, рис. 2, б] и [1, рис. 2, г].

Аномальность экспериментальных результатов v = f ( T ) и, следовательно, G = f ( T ) , проявляемая в различных температурных интервалах спектра Л = f ( T ) , может быть описана при введении понятия дефекта модуля A G [16]:

Gо (To)-Gi (T) = v о2 (To)-v2 (T)

G о ( T o )              v o² ( T o )

Характер отклонений (аномальность) A v ² ( T ) , а следовательно, и A G ( T ) для различных локальных по температуре участков спектра к = f ( T ) в одной исследуемой системе может быть различным, зависящим от структурных атомномолекулярных образований в каждой структурнокинетической подсистеме. То есть значения аномальности могут быть в виде A v ² >  0 и A G >  0 и в виде A v ² <  0 и A G <  0 (при условии повышения температуры исследуемой системы).

Различие в знаках дефекта модуля A G позволяет провести условную классификацию локальных диссипативных процессов в соответствующих температурных интервалах спектра внутреннего трения к = f ( T ) :

( A v ² >  0; A G >  0 )    ^ релаксац. мех.,

< ( A v ² <  0; A G <  0 )    ^ фазовый мех., (22)

(Av2 » 0; AG « 0)r ^ гистерез. мех., где + T — индекс, указывающий на нагревание; релаксац. — релаксационный; мех. — механизм; гистерез. — гистерезисный.

В случае охлаждения будет обратная картина.

Таким образом, пики диссипативных потерь могут иметь релаксационный или фазовый механизмы внутреннего трения, а фон диссипативных потерь на спектре к = f ( T ) имеет гистерезисный механизм внутреннего трения вплоть до температур T ≪ T g .

ФОН ДИССИПАТИВНЫХ ПОТЕРЬ НА СПЕКТРЕ к = f ( T )

Наличие на спектрах к = f (T) отличного от нуля фона потерь кфон * 0, имеющего значительно меньшую интенсивность, чем пики потерь, налагающиеся на этот фон λ ≪ λ , позволяет maxфон         imax отнести процесс образования фона к явлениям не-упругости гистерезисного типа [17–34].

Проявление явлений неупругости гистерезисного типа, как правило, наблюдается в режимах внешнего деформирующего воздействия, при котором напряжения σ , возникающие в образцах исследуемых систем, не превышают предела упругости σ_упр :

ст < ст < ст ,                     (23)

пр             упр , мгновенное взаимно-однозначное соотстветвие "ст - f,              <25

где σ_пр — предел пропорциональности, гуковская мгновенно-однозначная (не зависящая от времени) взаимосвязь (напряжение — деформация) (" ст - у" * f ( t ) ); О упр — предел упругости (упруговязкая неупругая взаимосвязь "ст - у" = f ( t ) ).

В интервале напряжений (23) реакция системы на внешнее деформирующее воздействие, выводящее эту систему из состояния механического и термодинамического равновесия, может быть описана феноменологической моделью Кельвина – Фойгта [4]:

ст = Gy + nY-                  (24)

Однако при напряжениях ст <  ст пр интенсивность фона диссипативных потерь не стремится к нулю, а практически не изменяется, что свидетельствует об определенной глобальной диссипа-тивности отклика системы на внешнее воздействие во всем температурном интервале существования конденсированного состояния этой системы.

Это отклонение от гуковской реакции ст=f (Y).

• _<    Уост = ⁰, ^ст * ^{f (} t ) , Y * f ( t )

^ст = ^{f ( Y} ) ,

• _<    Уост = 0, ^ст = ^{f (} t ) , . Y = f ( t )

регистрируется на диаграмме " ст - у " в виде эллипсоидных петель гистерезиса, где площадь петли гистерезиса определяет диссипативные потери в исследуемой системе.

В образовании фона диссипативных потерь на спектре к = f ( T ) принимают участие структурно-кинетические элементы всех подсистем: как агрегатной, так и ряда модифицирующих подсистем [12].

Вклад каждой из данных подсистем в образование фона зависит от температуры и может быть незначительным по интенсивности, но общий суммарный вклад будет определять общую интенсивность фона на спектре [1, рис. 2, а].

Таким образом, каждой структурнокинетической подсистеме будет соответствовать свой гистерезисный петельный эллипс определенной площади, которая и характеризует диссипативный вклад данной подсистемы в интенсивность не мгновенное (затянувшееся во времени) соотстветвие "ст - у"

общего фона диссипативных потерь на спектре X = f ( T ) [2].

Структурно-кинетические подсистемы могут быть образованы различными атомно-молекулярными образованиями исследуемой системы. Например, для кристаллических низкомолекулярных систем, структурно-кинетические подсистемы могут быть образованы дислокациями или точечными дефектами (атомы внедрения, атомы замещения и т.п.). Процесс взаимодействия этих элементов при их стремлении занять при изменении температурно-частотных режимов внешнего воздействия более выгодные для данных условий энергетические положения приводит к противодействию со стороны элементов других подсистем, энергетическое положение которых еще не позволяет совершать подобные переходы [13–15]. В частности, процесс взаимодействия колеблющихся дислокационных образований структуры с точечными дефектами может быть представлен как процесс взаимодействия одной структурнокинетической модифицирующей подсистемы с другой, что представится как дислокационный вклад в интенсивность фона диссипативных потерь на спектре X = f ( T ) . Данный процесс характеризуется как гистерезисный механизм внутреннего трения в образовании фона на спектре X = f ( T ) .

Несмотря на качественную простоту обоснования появления на спектре внутреннего трения X = f ( T ) фона диссипативных потерь, количественное описание температурной, частотной и амплитудной зависимостей диссипативных потерь для этого фона представляет собой сложную проблему, требующую большого массива экспериментальных данных.

Следует отметить, что начало подобным исследованиям было положено в работах [17–32], в которых исследуемая система рассматривалась в рамках феноменологических моделей однородного непрерывного сплошного тела.

В более поздних работах гистерезисный механизм образования фона диссипативных потерь на спектрах внутреннего трения X = f ( T ) рассматривается на базе модельных представлений об атомно-молекулярном строении исследуемых материалов [10, 33–35].

Реакция исследуемой системы как непрерывного однородного сплошного тела, в соответствии с условиями (26), когда вязкость η * этой системы η * ≫ 1014 Па·с → ∞ (η* — вязкость "замороженной" подсистемы) [1, рис. 2, в], и в то же время имеются диссипативные явления в этой системе, т.е. A W Ф 0, не позволяет непосредственно ис- пользовать в описании этой реакции модельные представления Кельвина – Фойгта и Максвелла (вследствие условия п* ^^) [4]. В этом случае необходимо принять гипотезу, что феноменологически описать диссипативные гистерезисные явления при условиях (26) возможно в случае, когда феноменологическая модель каждой структурнокинетической подсистемы будет рассматриваться как квазиупругая модель, включающая в себя три компоненты (рис. 2):

• 1)    элемент замороженной вязкости всей исследуемой системы η * ≫ 10¹⁴ Па·с → ∞;

• 2)    модуль сдвига G i (для каждой подсистемы различный);

• 3)    локальный диссипативный элемент r_i ≠ 0 при σ <  σ np , различный для разных структурно-кинетических подсистем.

Диссипативный элемент r_i соединен параллельно с упругим элементом G_i , что позволяет рассматривать гистерезисный механизм внутреннего трения и отсутствие остаточных деформаций во всей системе Y_ocm = 0.

Модель подобного типа была предложена академиком Каргиным при описании деформаций гибкоэластичных полимеров, состоящих из длинных цепей макромолекул [36].

Диссипативный элемент r_i может быть принят в качестве характеристическ о й силы внутреннего неупругого сопротивления F_r , которая противодействует любому перемещению элементов i -й структурно-кинетической подсистемы.

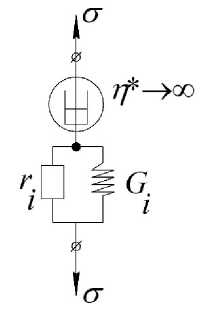
Рис. 2. Феноменологическая модель для описания гистерезисного механизма внутреннего трения, проявляемая на спектрах X = f ( T ) в виде фона диссипативных потерь

Именно эта сила F_r и является причиной возникновения эллиптической гистерезисной петли с обхватом площади S_rucm = A W 0 , равной величине диссипируемой энергии A W T за один период колебательного процесса при изотермическом режиме T = const, при о <  о пр , где о пр — предел пропорциональности i -й структурно-кинетической подсистемы.

Для определения силы F_r было предложено две теории [17–32]:

• 1)    сила F_r зависит от скорости (частоты ω ) деформации Y , ^т-^е- F_r, = f ( Y ) ;

• 2)    сила F_r зависит от амплитуды деформации γ _max ( ϕ _max ) колебательного процесса, т.е. ^F i = ^f ( Y 0 ) , или F = f ( ф о ) , где Ф тах ^{— ампли}тудный угол деформационного сдвига.

В частотной зависимости F r = f ( to ) рассматривается как линейная связь, так и нелинейная связь между силой локального неупругого сопротивления F_r элементов i -й структурнокинетической подсистемы и частотой колебательного процесса, возбуждаемого как в i -й подсистеме, так и во всей системе в целом.

В амплитудной зависимости F r = f ( ф _тах ) также рассматривается два направления: линейная и нелинейная зависимости.

При свободно затухающем колебательном процессе, возбуждаемом в образцах исследуемой системы, диапазон частот составляет от 10–1 Гц до ~10 Гц при заданных геометрических размерах образцов для устройства [16], поэтому основное внимание в этом случае уделяется выполнению условия г, „ = const, т.е. Ф я „ = const, и выполне-max                    max нию условия амплитудно-независимого внутреннего трения для каждой i-й подсистемы:

^ <  ^С к * f ( ф тах ) ,

где σп — предел пропорциональности -й струк-пр турно-кинетической подсистемы, входящей в общую систему исследуемого материала.

Таким образом, в образование фона внутреннего трения вносят свой вклад все структурнокинетической подсистемы исследуемой системы.

Вклад каждой подсистемы в фон различен и определяется температурой исследования, поэтому наиболее стабильным и относительно постоянным в широком температурном режиме ис- следований к = f (T) является фон внутреннего трения агрегатной формообразующей подсистемы [13–15].

Фон внутреннего трения для системы, состоящей из одной структурно-кинетической подсистемы, которая в этом случае является агрегатной и формообразующей подсистемой, например для бездефектных монокристаллических систем [1, рис. 2, а; рис. П1], состоит из двух температурных областей:

• 1    — линейная зависимость от температуры, область АБ [1, рис. 2, а];

• 2    — нелинейная зависимость от температуры, область БД [1, рис. 2, а].

В этом случае исследования спектров внутреннего трения в широком температурном интервале необходимо проводить в таких режимах, чтобы свести к минимуму влияние частотно-зависимой составляющей внутреннего трения и амплитуднозависимой составляющей с выполнением соотношений (27).

Режимы частотно-независимого (ЧНВТ) и амплитудно-независимого внутреннего трения (АНВТ) в данном методе используются для того, чтобы были созданы условия неразрушения образованных в системе структурно-кинетических подсистем и возможности корректного использования соотношений феноменологических модельных представлений и положений теории линейной вязкоупругости Больцмана – Вольтерра [37].

При этом следует отметить, что даже выполнение условий ЧНВТ и АНВТ не является препятствием для смены механизма внутреннего трения фона диссипативных потерь на спектре к = f ( T ) :

• –    до температур стеклования T_g или кристаллизации T_cr агрегатной структурно-кинетической подсистемы ([1, рис. 2, а] — участок АБ) механизм внутреннего трения является гистерезисным;

• -    после температур T >  T_g или T >  Т_сг механизм внутреннего трения изменяется от ЧНВТ гистерезисного типа на релаксационный механизм с частотной зависимостью и выполнением условий принципа температурно-временной суперпозиции.

Итак, гистерезисный механизм внутреннего трения, определяемый по температурным спектрам внутреннего трения к = f (T) в интервале температур до температур T < Tg или T < Тсг (где Tg или Tсr — температуры изменения агрегатного состояния всей системы или агрегатной формообразующей подсистемы), является амплитудно-и частотно-независимым в режиме исследований методом свободно затухающего колебательного процесса в диапазоне частот от ~10–1 Гц до 10 Гц при возникновении в образце исследуемой системы напряжений, меньших предела пропорциональности σпр , и характеризует фон диссипативных потерь на спектре ([1, рис. 2, а] — участок АБ).

В области гистерезисного механизма фона внутреннего трения на спектре к = f ( T ) температурное изменение частоты свободно затухающего колебательного процесса, возбужденного в образце, происходит монотонно без аномальностей и составляет ~(2÷4)% на каждые 100 град. температуры.

В области температур T >  T g или T >  Т_сг фон диссипативных потерь на спектре к = f ( T ) бездефектной монокристаллической системы начинает резко возрастать ([1, рис. 2, а] — сплошная линия).

Аналогичное изменение фона диссипативных потерь на спектре к = f ( T ) характерно и для агрегатной формообразующей подсистемы многокомпонентной системы ([1, рис. 2, а] — участок БД).

Если для этого температурного интервала спектра ([1, рис. 2, а] — участок БД) рассматривать развертку колебательного процесса [1, рис. 1, в] Ф = f ( t ) , то в координатах "ст - у " будет иметь место совокупность незамкнутых эллиптических кривых (рис. 3).

При теоретическом анализе этого явления с энергетических позиций следует, что потенци- альная энергия системы в i-м периоде колебательного процесса ([1, рис. 1, г]; рис. 3) определяется соотношением:

U i = G уТ .                 (28)

Для ( i + 1)-го периода потенциальная энергия:

γ ²

и ( , . , ) = G -^.                (29)

Рассматриваемый затухающий колебательный процесс (рис. 3) с энергетических позиций определяется величиной энергии U , сообщаемой системе в каждый период колебательного процесса, а величина U определяется площадью эллипсоидной петли каждого колебания.

Для определения U_i каждого периода колебательного процесса (т.е. площади петли гистерезисной кривой ( " ст - у " ) ) необходимо принять следующие допущения:

• 1)    незамкнутостью петли гистерезисных потерь для каждого i -го периода колебаний можно пренебречь;

• 2)    уменьшение амплитуды А у значительно меньше величины самих амплитуд y i , У ( i _{+ 1} ) , „. каждого периода колебательного процесса:

^А у « Y i « у ₍ i + 1 ) «.„             ⁽3⁰⁾

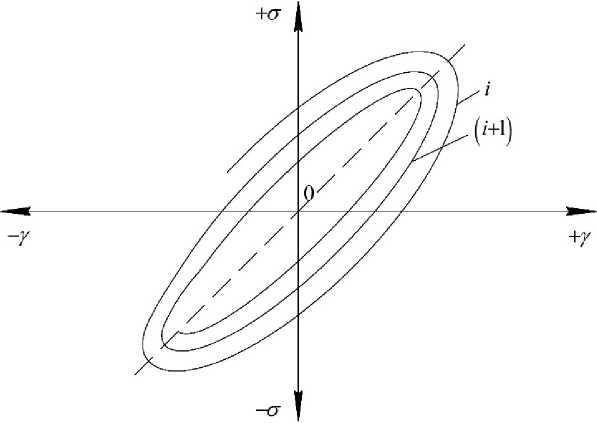
Рис. 3. Система эллиптических незамкнутых петель, характеризующих диссипативные потери для каждого периода затухающего колебательного процесса, возбужденного в исследуемой системе

Таким образом, разность A U между периодами колебательного процесса будет соответствовать диссипированной за период величине энергии, т.е.:

AU — U, - U(,+1} = G(у, - Y.. ) * G(у, • Ay,). (31)

Площадь незамкнутой гистерезисной петли, соответствующей амплитуде γ , определяется соотношением [18–20]:

S , — 2 k R , y , ,                 (32)

где k — коэффициент формы петли; 2 R — наибольшая ширина петли гистерезиса.

Коэффициент формы определяется соотношением [18–27]:

k —

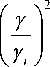
процесса ([1, рис. 1, в, г, д], штриховая линия) в виде

А у , =- У-у ,             (37)

dt где θ — период колебания, то это уравнение с учетом соотношения (36) может быть представлено в виде:

a(Y*)n =-в to .(38)

Интегрируя уравнение (38) методом разделения переменных и c условием, что n Ф 1, получаем соотношение:

(Y, Гn)«>

—г C

1 - nв

Постоянная интегрирования С в уравнении (39) определяется при начальных условиях

Если принять, что сила F_r неупругого сопротивления материала исследуемой системы пропорциональна ширине петли R для n -й степени амплитуды γ , тогда:

F r , ~ R o , 4 Y , ) n — b ( Y , ) n ,          (34)

ft — 0, Y- — Y max (Y    )(1-n) ^ C — max ---. 1 - n (40) Таким образом: (Y,)"-n' — at , ( Ymax )(1-n) +              . (41) 1 - n в     1 - n где R0 — начальная полуширина петли гистерезиса, b — коэффициент, ^ — символ пропорциональности.

Из соотношений (32) и (34) следует:

Откуда уравнение огибающей развертки затухающего колебательного процесса определяется в виде:

S , — 2 k b ( y,} n ⁺ 1 .                       (35)

Таким образом, из соотношений (31) и (35) следует:

γ max

^{( n} -i/l + ^ n -¹ а (у   )⁽ n ^-1)t

θ γ max

Для случая n — 1 уравнение (38) принимает

^A U , = S , ^ ^G ( Y , • ^a Y , ) = ^{2 k b} ( Y , ) n ⁺ 1 , .       2 k b ( y ,}n ⁺ 1

^a Y , =---_        = a ( Y , ) ,

Gγ max

вид:

2k b где a — ——характеристика жесткости образца.

Из соотношения (36) следует, что если сила неупругого сопротивления F_r является малой и пропорциональной n -й степени амплитуды деформации (соотношение (34)), то убывание амплитуды деформации A y , также пропорционально n -й степени амплитуды ( у , ) n .

Если рассматривать дифференциальное уравнение огибающей затухающего колебательного

a(у) — -вdY. ^ dYt — -О(У) ^ dt    dtθ dγ    aa

^^^ — — dt ^ ln у —— t + C, γ   θθ

где постоянная интегрирования С определится в виде:

t — 0,

Y , ^— Y max

^

C — In у

max .

Таким образом, из соотношений (43) и (44) следует:

t

^1П Y i = - a + 1П Y max θ

^ 1n -^ =

γ max

t

—a ^ θ

^ y. = y e i max

t

—a θ .

Соотношение (45) представляет собой функцию релаксации вязкоупругой реакции феноменологической модели Максвелла, где время релаксации совпадает с периодом колебательного процесса, т.е. т ^ 9 [4].

Таким образом, фон внутреннего трения при температурах T ≫ T_g или T ≫ T_cr может быть описан в рамках теории неупругости Больцмана – Вольтерра как вязкоупругий релаксационный процесс.

Одновременно с возрастанием интенсивности фона диссипативных потерь на спектре к = f ( T ) в этом же интервале температур на зависимостях модуля сдвига G = f ( T ) и частоты колебательного процесса v = f ( T ) наблюдается отклонение

от теоретических кривых для этих характеристик [1, рис. 2, б, г].

Это отклонение характеризуется дефектом модуля (соотношение (21)) и представляет собой релаксационный модуль G ( t ) описываемый соотношением (13) с простой дробно-экспоненциальной функцией релаксации 9 i ( t ) — максвелловской экспонентой, аналогичной экспоненциальной функции изменения огибающей развертки затухающего колебательного процесса.

ЗАКЛЮЧЕНИЕ

Представлен метод теоретического анализа физико-механических и физико-химических характеристик различных диссипативных процессов, проявляемых на спектрах внутреннего трения и температурно-частотных зависимостей, с использованием представлений об исследуемом материале как совокупности квазинезависимых структурнокинетических подсистем, составляющих в совокупности исследуемую систему.

ПРИЛОЖЕНИЕ

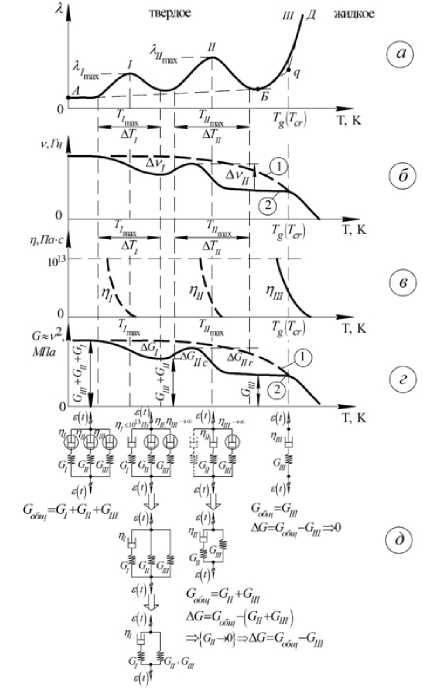
Рис. П. Схематическое обобщение спектра внутреннего трения для пиков локальных диссипативных потерь.

Построено на [1, рис. 2] и рис. 1