МЕТОДИКА ИССЛЕДОВАНИЯ ВНУТРЕННЕГО ТРЕНИЯ В РЕЖИМЕ СВОБОДНО ЗАТУХАЮЩЕГО КОЛЕБАТЕЛЬНОГО ПРОЦЕССА. Ч. 3. МЕХАНИЗМЫ ВНУТРЕННЕГО ТРЕНИЯ

Как было отмечено в первой [1] и второй [2] частях данной статьи, на фон диссипативных потерь на спектре X = f (T) в различных температурных участках этого спектра накладываются пики λ диссипативных потерь [1, рис. 2, а], imax проявление которых связано с подвижностью элементов различных структурно-кинетических подсистем.

Обнаруживаемые на спектре X = f (T) пики диссипативных потерь могут иметь различную интенсивность X * X * X , различное Imax       IImax       IIImax структурно-кинетическое происхождение и различный механизм внутреннего трения:

– релаксационный;

– фазовый;

– смешанный (гистерезисно-релаксационный).

РЕЛАКСАЦИОННЫЙ МЕХАНИЗМ ВНУТРЕННЕГО ТРЕНИЯ

Релаксационный механизм внутреннего трения рассматривается на примере полиэтилена (ПЭ) марки CRP 100 Hostalen, гранулы которого получены с применением процесса Hostalen — суспензионной полимеризации в мешалочных реакторах [3].

Суспензионную полимеризацию Hostalen проводят в двух реакторах, работающих параллельно или последовательно. Переход с одного реактора на каскад дал возможность вырабатывать на одном и том же катализаторе высококачественный одно- и бимодальный полиэтилен с любым молекулярно-массовым распределением. Полимеризацию проводят в растворителе, например в н-гек-сане, на высокоактивном катализаторе Циглера. По окончании процесса не требуется деактивация катализатора и извлечение его из полимера, т.к. концентрация остаточного катализатора в полимере очень мала. Для получения одномодального продукта катализатор, растворитель, мономер и водород вводят в реакторы 1, 2, где протекает полимеризация. Для получения бимодальных марок катализатор вводят только в реактор 1; вторая стадия полимеризации протекает в условиях, отличающихся от условий первого реактора. В реактор 2 вводят этилен, бутен и дополнительное количество растворителя. Условия процесса непрерывно регулируют, что обеспечивает получение полиэтилена очень высокого качества [3] (см. табл. 1).

На рис. 1 представлены полученные спектр внутреннего трения X = f ( T ) и температурная зависимость частоты v = f ( T ) свободных затухающих крутильных колебаний, возбуждаемых в исследуемом образце в интервале температур от - 150 ° C до + 150 ° C.

Табл. 1. Основные физико-химические характеристики ПЭ CRP 100 Hostalen, согласно паспортам производителей и требованиям по ТУ

№	Марка ПЭ	CRP 100 Hostalen
1	Тип сомономера	Бутен
2	Молекулярно-массовое распределение (полидисперсность)	Бимодальный
3	Плотность ( ρ ) при 23 ºС, (г/см3)	0.960
4	Показатель текучести расплава (ПТР), г/10 мин при 190 °С и 21.6 кгс при 190 °С и 5.0 кгс	6.4 0.23
5	Температура плавления ( Т пл ), °С	131
6	Энтальпия плавления (Δ Н ), Дж/г	132.4
7	Степень кристалличности ( α )*, %	45

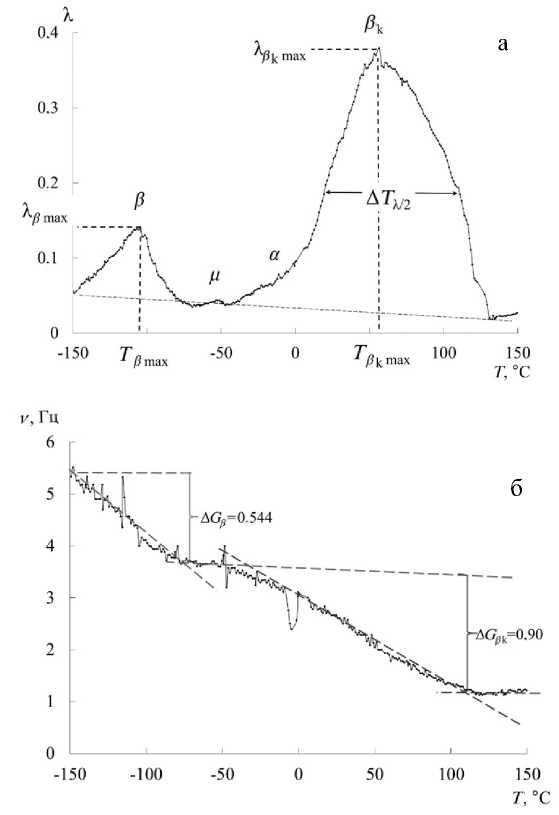
Рис. 1. Спектр внутреннего трения X = f ( T ) — (а), и температурная зависимость частоты v = f ( T ) — (б) для ПЭВП марки CRP 100 Hostalen

Скорость нагрева исследуемого образца в термокриокамере устройства составляла 2°/мин.

На спектре X = f ( T ) наблюдаются две температурные области наиболее интенсивных локальных диссипативных процессов ( β и β _k ). Температурные области проявления этих процессов частично совпадают с данными, опубликованными ранее [4-11]. Кроме того, на спектрах X = f ( T ) и температурных зависимостях частоты v = f ( T ) свободно затухающего колебательного процесса выявлены две температурные области с очень слабой интенсивностью локальных диссипативных процессов. Предполагаем, что это α — диссипативный процесс, практически полностью поглощенный наложением низкотемпературной ветви β _k -процесса, и μ- процесс, наблюдаемый в области температур ~- 70 ° C.

Одновременно с измерением логарифмического декремента λ затухающего колебательного процесса проводилось исследование и температурной зависимости частоты колебательного процесса, возбуждаемого в исследуемом образце ПЭ (рис. 1, б). Температурные зависимости частоты v = f ( T ) свободных затухающих крутильных колебаний, возбужденных в исследуемом образце ПЭ, указывают температурные области аномального изменения частоты в тех интервалах, в которых на спектрах X = f ( T ) наблюдаются пики диссипативных потерь.

Для β - и β k -диссипативных процессов на спектре X = f ( T ) в соответствующих этим процессам температурных интервалах на температурной зависимости частоты v = f ( T ) колебательного процесса наблюдается локальное по температуре и относительно резкое снижение частоты ν колебательного процесса (рис. 1, б).

Проведен расчет физико-механических и физико-химических характеристик для β - и β k -про-цессов диссипативных потерь по приведенным ранее формулам, согласно которым из соотношения [2, (5)] следует, что текущее по температуре изменение λ_i достигает своего максимума на пике потерь ( X i = Х_д ) при выполнении условия:

®т , - 1,                           (1)

где время релаксации τ_i есть функция температуры T_i , т.е. соотношение [2, (6)]:

U β

Т = т 0 exp^ kma~ ,                 (2)

RTi

где U — энергия активации диссипативного βk max процесса; т0 ~ 1.6 -10—13 c — теоретическое значение предэкспоненциального коэффициента, характеризующего колебательный процесс релаксирующей частицы на дне потенциальной ямы. Частота колебательного процесса ν (определяемая экспериментально по зависимости v = f (T)) связана с круговой частотой ω соотношением: to = 2nv. Это позволяет определить время релаксации т = тmax в пике локальных диссипативных потерь λmax по соответствующей этому значению величине частоты v = vmax на температурной зависимости v = f (T) по соотношению вида:

^to max ^T max   ^{2 n v} max ^T max   ^{2 п} ^Т=Т ^11=1 )   ¹ ^

max        max

^ ^{т (} T - T max )    1- _v

^{2 П v} ( T - T max )

.

Исходя из экспериментальных данных и соотношения (3), получим:

^т в =

2 • n • 4.35

- 0.037 с;

^т в _к ^-

2 • п - 1.94

- 0.082

с.

Энергия активации данного процесса определяется из аррениусовской зависимости времени релаксации τ от температуры (соотношение (2)) с учетом (3) в виде:

τ

U_R  - RT_r  ln ^ma^ -

β max         β max

τ ₀

- 8.314 - 167 - ln

0.037

1.6 - 10 ^{- 13}

- 36330.93

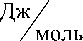
36.4

(В (4) температура указана в °К).

Полученные физико-механические и физикохимические характеристики для β - и β k -процессов диссипативных потерь представлены в табл. 2.

Для того, чтобы определить механизм внутреннего трения для каждого из обнаруженных на спектре внутреннего трения X - f ( T ) (рис. 1, а) диссипативных процессов, необходимо провести расчет дефекта модуля сдвига, что производится на базе экспериментально полученной температурной зависимости частоты колебательного процесса, возбужденного в исследуемых образцах ПЭ. Каждый локальный диссипативный процесс, наблюдаемый на спектре X - f ( T ) , характеризуется

Табл. 2. Основные физико-механические и физико-химические характеристики для β - и β k -процессов диссипативных потерь

№ п/п Процесс Tmax, °C λmax νmax, Гц Uα, кДж/моль τmax 1 β-процесс –106 0.138 4.35 36.4 0.037 2 βk-процесс 57 0.379 1.94 73.9 0.082 своим температурным интервалом, величиной и знаком дефекта модуля AGi. Величина дефекта модуля AGi определяется из соотношения, учитывающего связь изменения частоты колебательного процесса, возбуждаемого в исследуемом образце, и изменения модуля сдвига материала этого образца [12]. Учитывая то, что в используемом устройстве исследуемый образец является составной частью колебательной системы, крутильные колебания, возбуждаемые в исследуемом полимере, могут рассматриваться как моды собственных колебаний, где для затухающего процесса берется только первая мода [13]. В этом случае связь между динамическим модулем сдвига G и частотой ν колебательного процесса определяется в виде:

где G — модуль сдвига материала исследуемого образца; I_a — полярный момент инерции поперечного сечения относительно продольной (полярной) оси исследуемого образца; I_S — полярный момент образца; I — полярный момент инерции дополнительных полюсных наконечников системы возбуждения крутильных колебаний, ось которой совпадает с продольной осью образца; l — длина исследуемого образца. Если в первом приближении температурными изменениями моментов инерции колебательной системы устройства можно пренебречь, то соотношение (5) может быть представлено в виде:

G ~ ку 2 .

v =

G • I a

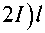
7,4

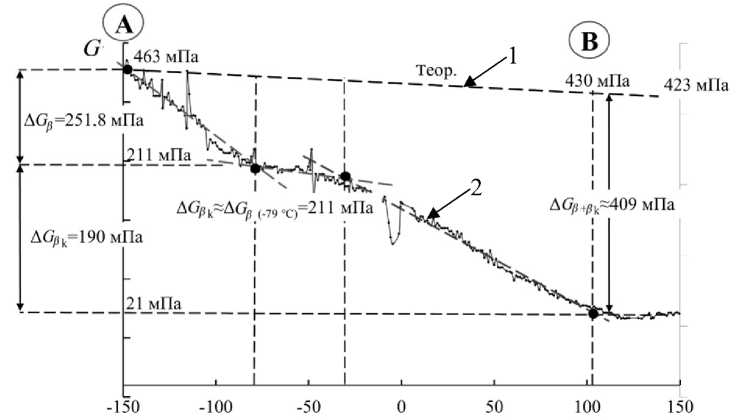
Рис. 2. Температурная зависимость модуля сдвига ПЭ.

1 — теоретическая зависимость, штриховая прямая; 2 — кривая, рассчитанная с учетом дефектов модуля для β - и β k -релаксационных процессов для ПЭПВ марки СRP 100 Hostalen

Однако было экспериментально установлено, что модуль сдвига G является функцией от температуры, т.е. G = f ( T ) ^ G ( T ) . Теоретическая зависимость G = f ( T ) при повышении температуры на каждые 100 град соответствует линейному снижению модуля G на 2÷4% [14] (рис. 2, штриховая линия).

В этом случае частота ν колебательного процесса также будет зависеть от температуры, т.е. v = f ( T ) = v ( T ) и будет изменяться пропорционально температурному изменению модуля сдвига G ( T ) , т.е.:

G ( T ) к 2 - v ² ( T ) k i ,                (7)

где k ₁ и k ₂ — постоянные коэффициенты.

Так как k ₁ , k ₂ — const, соотношение (7) может быть представлено в безразмерной форме, т.е.:

где на спектрах внутреннего трения к = f ( T ) наблюдаются локальные диссипативные процессы в виде пиков потерь, наблюдается аномальное изменение температурной зависимости частоты ν , а следовательно, и модуля сдвига G , вызываемое значительными отклонениями от пропорциональной теоретической температурной зависимости G = f ( T ) или v = f ( T ) . Для описания этой аномальности вводится понятие дефекта модуля сдвига или дефекта частоты. Дефект модуля определяется как безразмерная величина в виде соотношения [2, (21)], представленного ранее:

A G ( T ) =

G о ( T o ) - G , ( T ) = v o ² ( T o ) - v i ( T ) G o ( T o )             v 2 ( T o )

Исходя из экспериментальных данных и этого выражения, получим:

G ( T ) к 2 G 0 ( T o ) к 2

v i ( T ) k i v 02 ( T o ) к 1

>A G ( T ) «A v ² ( T ) ,

A G e

5.51² - 3.72 2

5.512

= o.544;

где G , ( T ) и v , ² ( T ) — текущие по температуре T значения модуля сдвига G_i и квадрата частоты ν_i ² ; G _o ( T _o ) и v _o ² ( T _o ) — при выбранной температуре T ₀ начальные значения модуля сдвига G ₀ и квадрата частоты ν ₀² .

Таким образом, температурное изменение частоты v ( T ) колебательного процесса, возбужденного в исследуемой системе, позволяет определить и температурное изменение модуля сдвига G ( T ) материала, из которого изготовлен исследуемый образец. Однако экспериментальные данные исследования зависимости v = f ( T ) показывают, что в определенных температурных интервалах,

^{A G} e _t

3.62² - 1.14²

3.622

= o.9oo.

Каждому локальному диссипативному процессу, обнаруженному на спектре внутреннего трения к = f ( T ) в различных интервалах температур, соответствует определенная аномалия в температурной зависимости частоты колебаний v = f ( T ) , а следовательно, и модуля сдвига G = f ( T ) , что и приводит к локальной по температуре области неупругости исследуемой системы. В общем случае для каждого -го пика диссипативных потерь, обнаруживаемого на спектре внутреннего трения к = f ( T ) , будет наблюдаться на температурной зависимости частоты колебаний v = f ( T ) свой дефект модуля сдвига A G , ( T ) .

Табл. 3. Теоретические и расчетные данные по результатам эксперимента для исследуемого образца ПЭВП

№ п/п	Процесс	Т , °С		Диапазон изменения частоты, Гц		Дефект модуля Δ G
		от	до	от	до
1	β -процесс	–147.97	–79.33	5.5122	3.7214	0.544
2	β k -процесс	–32.33	102.46	3.62	1.1428	0.900

Если учесть, что модуль сдвига G всей исследуемой системы образуется за счет сложения модулей G_i всех n структурно-кинетических подсистем, образующих данную систему, т.е.

n

Gi =2 Gi, i=1

то температурная зависимость модуля сдвига всей системы будет определяться в виде:

nn

G (T ) = ZGi( T )±ZA G( T).       (10)

i = 1                       i = 1

Дефект модуля сдвига может иметь положительное значение для диссипативных процессов релаксационной природы и отрицательное значение для диссипативных процессов нерелаксационной природы. Рассчитанные величины и знак дефектов модуля сдвига для β - и β k -процессов приведены в табл. 3.

Расчет дефектов модуля A G для исследованного образца ПЭ показал, что β - и β k -процессы имеют релаксационный механизм внутреннего трения.

ПРИМЕР РАСЧЕТА G = f ( T )

ДЛЯ ИССЛЕДУЕМОГО ПЭВП МАРКИ СRP 100 HOSTALEN

Согласно паспортным данным, модуль упругости при растяжении E (23 °C) для данной марки равен 1100 мПа.

Таким образом, из пропорциональной зависимости следует:

G теор = 440 мПа ^ 100% I    440 • 1

> x =----- x         ^ 1%      100

4.4мПа

1%.

Снижение модуля упругости на ( 2^4 ) ® 3% означает его уменьшение на 4.4 × 3 = 13.2 мПа. То есть изменение температуры на 100 °С приводит к изменению модуля упругости для исследуемого образца на 13.2 мПа.

Изменение модуля на 1 °C — 0.132 мПа/1°.

Таким образом:

при 23 °C ^ G = 440 мПа;

при {| -150|+23 } °C = 173°C ^

^ 173 • 0.132 = 22.836 мПа » 23 мПа.

То есть: G –150 °C = G 23 °C + 23 = 440 + 23 = 463 мПа.

При { 150 - 23 } °C = 127 °C:

G _{+ 150} ° С = G ₂₃ ° С - 127 • 0.132 = 440 - 16.764 мПа =

= 423.236 мПа » 423 мПа.

Подставив в соотношение [2, (21)] экспериментальные данные по частоте из табл. 3, получим значения дефекта модуля сдвига для β - и β k -про-цессов. Графически расчет представлен на рис. 3.

Рассмотрим β - процесс.

Дефект модуля для β -процесса, как было сказано выше, определяется по формуле:

G теор

E

2 (1 + Ц)

2 ( 1 + 0.25 )

= 440 мПа,

A G (T ) = Av =

v 02 ( T 0 ) - v 2 ( T k ) v К ( T k )

где μ — коэффициент Пуассона, μ = 0.08÷0.45 ≈ 0.25.

При T = 23 ° C G _теор = 440 мПа.

5.5122² - 3.7214²

5.51222

= 0.544.

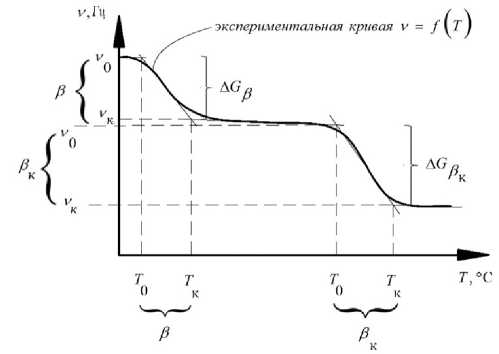
Рис. 3. Графическое изображение расчета дефекта модуля сдвига по экспериментальной кривой v = f (T)

При Т₀ =- 147.97 ° С и v 0 = 5.5122 Гц модуль упругости G _эксп ( _{- 148} ° С) = 462.7мПа - 463 мПа (получено приблизительно при экстраполяции G теор = f ( T ) на рис. 2 (линия 1) к температуре Т = - 147.97 -- 148 ° С).

За интервал температур β -процесса A T = Т к - T 0 = - 79.33 - ( - 147.97 ) = 68.64 ° С частота приняла значение v = 3.7214 Гц (рис. 1). Дефект модуля сдвига для β -процесса равен A G e = 0.544 в относительных единицах. Для определения значения модуля G_e при Т = - 79.33 ° С следует учесть, что при Т = - 147.97 - 148 ° С значение модуля сдвига равно G _эксп ( _{- 148} ° _С) = 463 мПа.

При температуре окончания β -процесса Т = - 79.33 ° С (табл. 3) модуль G_e уменьшился на величину A G_e = 0.544.

Для определения величины дефекта модуля сдвига A G e в абсолютных единицах используем соотношение:

^G эксп( - 32 ° С) ^{- G} эксп( - 79 ° С) = ^G эксп( - 148 ° С) ^{A G}p = = 463 мПа - 251.8 мПа - 211 мПа.

То есть изменение модуля сдвига всей системы теперь будет начинаться не с величины G _{( - 148} ° _С) = 463 мПа, а с величины G _эксп( _ ₇₉ ° _С) = = 211 мПа.

Таким образом, аналогично, как и для β -про-цесса, можно определить дефект модуля A G _e от величины G _эксп ( - ₇₉ ° _С) = 211 мПа, т.е.:

^G эксп( - 79 ° С)    ¹

A G_fl = 0.900 ^e k

.\ G e k = G эксп( - 79 ° С) • 0.900 =

= 211 - 0.900 = 189.9 - 190 мПа.

= 0.900 в относительных единицах от величины Gэксп(-79 °С) = 211 мПа,

A G« ^ ‘ β _k

^G эксп( - 148 ° С)    ¹

A G_e = 0.544

= 190 мПа в абсолютных единицах

от величины G_w, ₇₉    = 211 мПа.

ЭКсп ( /9 С)

^ A G p = G _Э кс _П ( _ 148 ° с) • 0.544 = 251.8 мПа.

= 0.544 в относительных единицах

Таким образом, в интервале температур проявления β k -процесса от –32 °С до +102 °С величина модуля сдвига уменьшилась на A G ^ = 190 мПа и составила:

^от величины ^G эксп( - 148 ° С)

^{A G} e >

= 251.8 мПа в абсолютных единицах от величины Gэксп(-148 °С) = 463 мПа.

G _Э ксп( + 102 ° С) = G _Э ксп( _ ₇₉ ° С) - A G e k = 211 - 190 - 21 мПа.

^G теор( + 102 ° С) ^—

- G эксп( - 148 ° С) - (| - 148+102) ° С - 0.132 =

= 463 - 33 = 430 мПа.

Таким образом, в интервале температур проявления β -процесса от –148 °С до –79.3 °С величина модуля сдвига уменьшилась на A G e = 251.8 мПа и составила:

^G эксп( - 79 ° С) = ^G эксп( - 148 ° С) - ^{A G} p =

= 463 мПа - 251.8 мПа - 211 мПа.

См. рис. 2.

Рассмотрим β k - процесс.

Для     β k -процесса    при температуре

Т = - 32.33 ° С (табл. 3) модуль сдвига всей системы после окончания β -процесса будет равен приблизительно:

A G =G  -Tag , эксп теор              i , i=1

где ^ A G_t — сумма всех дефектов модуля, т.е. i = 1

У A G =A Gfi +A Gfi . i        β        βk i=1

В этом случае в интервале температур от –147 °С до +102 °С значение модуля сдвига уменьшилось на величину, равную:

AGэксп = Gтеор(т.в.) Gэксп(+102 °С) = итеор (+102 °С) '-'эксп(+102 °С) ~

« 430 мПа - 21 мПа « 409 мПа.

Величина модуля сдвига G _эксп ( _{+ 102} ° _С ) ~ 21 мПа будет соответствовать модулю высокой эластичности ПЭ.

ФАЗОВЫЙ И СМЕШАННЫЙ МЕХАНИЗМЫ ВНУТРЕННЕГО ТРЕНИЯ

Фазовый и смешанный механизмы внутреннего трения лучше рассматривать на примере сегнетоэлектрических кристаллических систем, обладающих возможностью при изменениях температуры изменять свою кристаллографическую структуру без смены агрегатного состояния, т.е. без перехода из твердого в жидкое состояние.

Такие преобразования связаны с атомными перестройками структуры кристаллической системы в области температуры Кюри T _K (фазовый переход II рода), что фиксируется на спектрах Л = f ( T ) [15, 16] и температурных зависимостях v = f ( T ) и позволяет отнести эти процессы к процессам, вызванным элементами структурнокинетических подсистем в результате их неупругой реакции на незначительные по величине (порядка 10^–10÷10^–14) внешние деформирующие воздействия [15–18].

Теоретический анализ получаемых в этом случае экспериментальных результатов позволяет получить следующую информацию:

– качественно определить (по зависимости v = f ( T ) ) механизм диссипативных потерь для того или иного процесса, вызывающего на спектре Л = f ( T ) пик потерь;

– различия в атомных механизмах перестройки структуры;

– о подвижности различных структурных дефектов в кристаллической решетке, где каждый тип структурного дефекта определяется как совокупность подобных элементов одной структурнокинетической подсистемы;

– о процессах взаимодействия элементов одних структурно-кинетических подсистем с элементами других структурно-кинетических подсистем, например доменных границ и дислокаций в кристаллической структуре исследуемой системы;

– о степени влияния всех выявляемых на спектрах Л = f ( T ) и зависимостях v = f ( T ) диссипативных процессов на физико-механические и физико-химические характеристики кристаллической системы в целом.

В данной части статьи будут рассмотрены только те диссипативные процессы, которые имеют фазовый или смешанный механизм внутреннего трения, т.к. гистерезисный и релаксационный механизмы были рассмотрены выше для других систем.

На зависимостях Q ^{- 1} = f ( T ) и f ² = f ( T ) для титаната бария [1, рис. 3] четко прослеживается связь между интенсивностью диссипативных потерь, температурой пиков диссипативных потерь, аномальным поведением частоты и структурными изменениями в данной кристаллической системе [15].

Все пики диссипативных потерь на спектре Q - 1 = f ( T ) и аномальности изменения температурной зависимости частоты f ² = f ( T ) свободного затухающего колебательного процесса, возбужденного в кристаллической системе BaTiO₃ , наблюдаются в области температур структурных фазовых переходов в твердом агрегатном состоянии данной системы в целом.

Эти фазовые структурные преобразования наблюдаются в следующих температурных интервалах:

• 1)    интервал от –150 °С до –75 °С — структурный переход из ромбоэдрической фазы ( 3m ) в ромбическую фазу ( mm2 ), т.е. ( 3m ^ mm2 );

• 2)    интервал от –75 °С до +25 °С — структурный переход из ромбической ( mm2 ) в тетраэдрическую фазу ( 4mm ), т.е. ( mm2 ^ 4 mm );

• 3)    интервал от +25 °С до +125 °С — структурный переход из тетраэдрической ( 4mm ) в тетрагональную ( m3m ) фазу, т.е. ( 4mm ^ m3m ).

При этом следует отметить характерную особенность изменения частоты на зависимости f 2 = f (T), которая заключается в том, что модуль G увеличивается на восходящей ветви пика диссипативных потерь структурного фазового перехода, а на нисходящей температурной ветви пика диссипативных потерь T > T значение модуля G уменьшается [1, рис. 3].

Такое поведение температурной зависимости частоты (модуля) существенно отличается от зависимости f2 = f (T) или G = f (T) для диссипа- тивных процессов релаксационной природы внутреннего трения [1, рис. 3].

На спектре Q 1 = f (T) и Af = f2 f02

= f ( T ) для

стеклообразующих низкомолекулярных систем xNa2O • 25B2O3 • (75-x)SiO2 [1, рис. П4] отчетливо фиксируются все структурные изменения в зависимости от соотношения компонентов, образую- щих эту некристаллическую систему, однако механизм внутреннего трения обнаруживаемых пиков диссипативных потерь остается релаксационным, частота (модуль сдвига) при повышении температуры монотонно снижается для обеих температурных ветвей пика потерь на спектре.

Таким образом, одним из основных отличий фазового механизма внутреннего трения от релаксационного механизма внутреннего трения является различие в температурных зависимостях частоты свободно затухающего колебательного процесса, возбуждаемого в исследуемых системах, наблюдаемых в тех интервалах температур, в которых на спектре Q ¹ = f ( Т ) проявляются пики диссипативных потерь:

• 1)    фазовый механизм диссипативных потерь связан с экстремальным изменением частоты;

• 2)    релаксационный механизм диссипативных потерь связан с монотонным изменением частоты.

Следует отметить тот экспериментальный факт, что фазовый переход, проявляющийся на спектре Q - 1 = f ( T ) и зависимостях v = f ( Т ) , может быть как фазовым переходом I рода, так и фазовым переходом II-го рода.

В этом случае для определения природы фазового перехода в режиме свободно затухающего колебательного процесса, возбуждаемого в образце исследуемой кристаллической структуры, требуется проведение эксперимента при двух различных условиях:

• 1 ) экспериментальное определение зависимостей Q - 1 = f ( Т ) и v = f ( Т ) при постоянной скорости нагрева образца, т.е. Т = const;

• 2 ) экспериментальное определение зависимостей Q - 1 = f ( Т ) и v = f ( Т ) в изотермических режимах при различных температурах, т.е. T = const.

При проведении экспериментов в условиях Т = const система будет все время находиться в неравновесном термодинамическом состоянии, и фазовый переход (если он есть) будет наблюдаться не при одной постоянной температуре T _ф , а в некотором интервале температур А Т ф .

При проведении экспериментов в условиях Т = const система при каждой температуре T_t будет находиться в термодинамически равновесном состоянии.

И в этом, и в другом случае на спектре Q - 1 = f ( Т ) будет наблюдаться пик диссипативных потерь, независимо от природы фазового перехода.

Трактовка природы фазового перехода может быть дана как в рамках модельных представлений аномальных изменений диссипативных процессов

Ландау – Халатникова [16] (релаксационный механизм), так и в рамках взаимодействия энергии деформационного затухающего колебательного процесса с тепловыми флуктуациями какого-либо обобщенного параметра перехода структуры системы из неравновесного в равновесное состояние [19] (флуктуационный термодинамический механизм).

Определение рода фазового перехода по спектру Q - 1 = f ( Т ) заключается в следующем. Проводится исследование влияния скорости изменения температуры Т = const:

• -    на температурное положение Т _ , макси- Q max

мума пика диссипативных потерь, т.е. Q ^{- 1}_max;

• -    на интенсивность пика Q ; max

• -    на форму пика диссипативных потерь.

Для фазового перехода I рода характерны следующие особенности, выявляемые по спектрам Q ^- 1 = f ( Т ) :

• -    интенсивность пика диссипативных потерь Q ^- 1 _max в окрестности температуры фазового перехода T _ф линейно зависит от скорости изменения T при постоянной частоте колебательного процесса v = const, т.е.

Q ^-L x = f ( Т ) _v ;              (11)

• -    интенсивность пика диссипативных потерь Q Lax в окрестности температур Т ф обратно пропорциональна частоте ν колебательного процесса, возбуждаемого в исследуемых керамических кристаллических системах при постоянном значении Т , т.е.

Q " 'max = f ^{f 1} ) ;               (12)

V v J T

• -    интенсивность пика диссипативных потерь Q Lax в окрестности температур Т ф при Т = const (изотермическом режиме) уменьшается с течением времени изотермической выдержки исследуемой кристаллической структуры образца, т.е.

Q Lax = f ( t ) T ^ Q Lax ^ 0 при ( t ) T ^ 0;   (13)

• -    внутреннее трение в виде пика диссипативных потерь на спектре Q ^{- 1} = f ( T ) непосредственно связано с кинетикой превращения системы из одного фазового состояния в другое.

Механизм внутреннего трения для пика диссипативных потерь при фазовом переходе I рода проявляется на спектре Q-1 = f (Т) в определенном интервале температур АТф, что отвечает представлениям о "размытых фазовых переходах" и флуктуационном характере зарождения новой кристаллической фазы в структуре исследуемой системы в результате возникновения зародышей закритического размера и их последующего роста [15].

Для фазового перехода II рода не наблюдается зависимостей (11–13).

Следует отметить, что пик диссипативных потерь, наблюдаемый на спектре Q - 1 = f ( Т ) , имеющий фазовый механизм внутреннего трения и связанный с кинетикой структурных преобразований в объеме исследуемых кристаллических систем вблизи температуры Кюри T _K (фазовый переход I рода в сегнетоэлектриках), расположен в некотором температурном интервале А Т ф .

Таким образом, фазовые переходы I рода , проявляемые на спектре, являются не точечными (процесс происходит только при одной постоянной температуре), а размытыми фазовыми переходами I рода , имеющими термофлуктуационный характер зарождения новой фазы системы в старой кристаллической фазе.

Теория точечных фазовых переходов I рода основывается только на феноменологических термодинамических положениях без рассмотрения атомно-молекулярного строения исследуемых систем — абстрактная, идеальная, бездефектная система.

В данном случае устойчивость существования данной фазы определяется одной точкой, которая соответствует определенной совокупности переменных параметров системы без учета различного вида флуктуационных процессов в данной системе.

Наличие температурного интервала А Т ф для реальных систем свидетельствует о наличии некоего параметра, характеризующего определенные отклонения в термодинамической устойчивости самих атомно-молекулярных образований в объеме кристаллической фазы.

Этот параметр в теории фазовых превращений называется параметром упорядочения ξ , а в теории внутреннего трения для релаксационных процессов — релаксационной микронеоднородностью перехода.

Для этих пиков диссипативных потерь фазовых процессов, в которых параметр упорядочения изменяется постепенно при изменениях температуры, введено понятие размытого фазового перехода I рода.

Параметр упорядочения ^ при Т = T K равен нулю.

ЗАКЛЮЧЕНИЕ

Наличие переходных процессов от неравновесного к равновесному состоянию неконсервативной системы, определяемых данным методом внутреннего трения в режиме свободно затухающего колебательного процесса, возбуждаемого в образцах исследуемых систем, приводит к термодинамической необратимости данного процесса и, как следствие этого, диссипации в исследуемой системе части энергии внешнего силового воздействия.

Диссипация энергии может быть обусловлена процессами следующих видов.

• 1.    Необратимыми процессами теплопроводности, возникающими при различных температурах в различных частях системы.

• 2.    Термодинамическими процессами при деформационных смещениях одних структурных элементов (или областей структуры) системы относительно других без конфигурационных структурных изменений.

• 3.    Термодинамическими процессами при деформационных смещениях одних структурных элементов (или областей структуры) системы относительно других с конфигурационными структурными изменениями.

• 4.    Процессы внутреннего трения, вызванные дефектами структуры:

а – точечные дефекты;

б – диффузия одиночных вакансий;

• в – переориентировка бивакансий;

• г – эффекты, обусловленные атомами внедрения;

• д – эффекты, обусловленные атомами замещения;

• е – параупругая релаксация;

• ж – дислокации;

з – колебательное движение дислокаций;

• и – скольжение дислокаций;

• к – возврат внутреннего трения;

• л – переползание дислокаций;

• м – поверхности раздела.

• 5 . Внутреннее трение при фазовых превращениях:

• а – аллотропическое превращение и распад пересыщенных твердых растворов;

б – упорядочение расплавов;

• в – превращение ферромагнетика и антиферромагнетика в парамагнетик;

• г – превращение сегнетоэлектриков в обычный диэлектрик;

• 6 . Внутреннее трение, обусловленное электронными и ионными процессами:

• а – потери, связанные с фононами и электронами;

• б – магнитоакустический резонанс;

• в – ферромагнетики и антиферромагнетики; г– магнитные потери;

• д – сегнетоэлектрики и антисегнетоэлектрики.

д – превращение проводника в сверхпроводник.

На базе экспериментальных данных (спектров внутреннего трения и температурных зависимостей частоты свободного затухающего колебательного процесса, возбуждаемого в образцах исследуемых систем различной химической природы, строения и структуры) представлена возможность расчетов различных физико-механических и физико-химических характеристик исследуемой системы, таких как:

• -    экстенсивные (энтропийные) и интенсивные (энтальпия, энергия Гиббса) параметры диссипативных процессов;

• -    температурно-частотные зависимости термодинамических параметров и функций;

• -    непрерывные спектры времен релаксации H ( т ) как для каждого локального диссипативного процесса h ( т ) , так и для всей системы в целом

n

H(т) = Ёh (^) ;

= 1

• -    температурно-частотные зависимости непрерывных спектров времен релаксации;

• -    различные коэффициенты, характеризующие температурно-частотную ширину спектров времен релаксации при использовании положений теории неупругости Больцмана – Вольтерра;

• -    дискретный спектр времен релаксации D ( т , max ) исследуемой системы;

• -    температурно-частотные зависимости дискретного спектра времен релаксации D ( т , max ) = f ( ^T , K ) . и D ( т , _ ) = f ( to ) ^ ;

• -    локальные диссипативные r и локальные упругие k коэффициенты каждого из обнаруженных на спектре внутреннего трения диссипативного процесса;

• -    температурно-частотные зависимости локальных диссипативных и локальных упругих хар^актер^истик       r = f ( T , K ) _to ,        r = ^f ( to ) _T , _K ,

• k , = f ( T , K ) _to , k = f ( ® ) _{T K} — механизмы внутреннего трения;

• - дефекты модуля сдвига для каждого из обнаруженных на спектре внутреннего трения и температурной зависимости частоты свободного затухающего колебательного процесса, возбуж-

• денного в образце исследуемой системы, диссипативного процесса.