Методика измерения радиуса кривизны рабочего профиля рельса при экплуатации железнодорожного транспорта в условиях открытых горных работ

Обоснование параметров и режимов работы железнодорожного транспорта горных предприятий с открытым способом добычи полезных ископаемых является важным направлением повышения экономической результативности предприятия.

Эффективность работы железнодорожного транспорта в условиях открытых горных работ определяется тяговой способностью локомотивов, на которую влияет много факторов и в первую очередь коэффициент сцепления бандажей колесных пар карьерных локомотивов с рельсами, который зависит от условий эксплуатации. К ним относятся: повышенные загрязненность рабочих поверхностей и уклоны рельсовых путей до 60 ‰, а также малые радиусы закруглений рельсового пути, минимальная величина которых находится в пределах 40–60 м; применение рельсов с повышенным износом; наличие передвижных рельсовых путей и, как правило, наличие неполноценного балластного основания. В статье в качестве цели ставится проведение исследований контактного взаимодействия колес локомотива для определения условий их работы, при которых влияние указанных негативных факторов будет снижено.

Предварительный анализ возможных методов исследований показал, что наиболее эффективным является метод, основанный на анализе энергетических процессов, происходящих в пятне контакта системы «колесо - рельс» при передаче вращающего момента. Одним из главных критериев этого энергетического анализа является коэффициент сцепления в пятне контакта системы «колесо -рельс», который в свою очередь зависит от многих эксплуатационных условий, в том числе - от фактической площади поверхностей взаимодействующих объектов [1—5].

Описание моделей контактного взаимодействия колеса локомотива и рельса

Решение задачи о контактном взаимодействии и возникающих при этом контактных напряжениях и деформациях впервые было дано Г. Герцем в 1882 г.

с применением методов теории упругости [6].

Значительная часть исследователей демонстрировали свои результаты в об- ластях исследования процессов трения между колесом и рельсом [7-9], влияния их на тепловые и другие режимы [10,11], взаимодействия между компонентами конструкций [12, 13], построения математических моделей, описывающих взаимодействие колеса локомотива и рельса [14—20], включая эксперименталь- ные исследования.

Для перекрещивающихся под прямым углом цилиндров (сопряжение системы «колесо - рельс») параметры длин полуосей эллиптического пятна контакта а и b определяются по формулам, приве- денным в [21]:

a = 1,397n 3/N^ ■ -rR-a4 E r + R b = 1,397nb 3/N^ ■ -rR-bN E r+R

,

где r и R - радиусы кривизны взаимодействующих профилей бандажа колеса локомотива и рельса соответственно; Nk и E - контактные напряжения и деформации соответственно; na и nb - коэффициенты, определяемые в зависимости от отношения r/R [21].

При силовом взаимодействии различных тел вращения (шарики и ролики подшипников качения, колеса железнодорожного подвижного состава, катковые опоры мостовых конструкций, цапфы и втулки подшипников скольжения и т.п.) в зоне контакта возникают контактные напряжения, величина которых при приложении нагрузки обратно пропорциональна площади контактируемых поверхностей. В свою очередь, площадь контакти-руемой поверхности (пятна контакта) колеса и рельса зависит от радиусов кривизны контактируемых поверхностей, определяемых по формуле (1). Обоснованные фундаментальные данные о контактном взаимодействии реальных шероховатых поверхностей (в отличие от Герца и его ближайших преемников - учеников, считающих контактирующие тела абсолютно гладкими) получены в работах [1, 22—28]. Полученные в результате вышеупомянутых исследований характеристики нашли подтверждение в работах других авторов [29-34].

Известно, что на карьерном железнодорожном транспорте в качестве тяговых единиц применяются локомотивы с электрической и тепловой тягой, тяговые агрегаты, работающие как на электрической, так и на тепловой тяге, а также мотор-вагонные думпкары.

В процессе работы профили колес тяговых единиц подвижного состава и рельсового пути в силу множества процессов, протекающих в зоне пятна контакта при передаче вращающего момента от колесной пары локомотива к рельсу, подвергаются значительным нагрузкам и подвержены износу. Для обеспечения рациональных значений контактных напряжений в пятне контакта пары «колесо - рельс» должно особое внимание уделяться выбору профиля их поверхностей катания.

Решение задачи уменьшения износа неразрывно связано с понижением контактных напряжений в зоне взаимодействия системы «колесо - рельс». В свою очередь, величина контактных на- пряжений, кроме нагрузки на ось, зависит от геометрических параметров взаимодействующих тел (формула (1)), а именно – от радиусов контактирующих поверхностей колеса r и рельса R.

В международной практике железнодорожного движения для обеспечения минимальных контактных напряжений при движении на прямых и вписанных в кривые участки железнодорожного пути используют специальные профили колеса и рельса, которые называют конформными. Согласно принятой международной терминологии - понятие конформности обозначает общее состояние контактирующих поверхностей профилей колеса и рельса, которые в зоне контакта имеют подобные очертания [20].

Целью настоящей работы является определение радиуса шлифовки поверхности изношенного в результате эксплуатации рельса для обеспечения конформного контакта колеса локомотива с рельсом. Задача может быть решена путем измерения геометрических параметров пятна касания колеса и рельса. В качестве модели принимается профиль рабочей поверхности рельса в виде сегмента окружности (рис. 1).

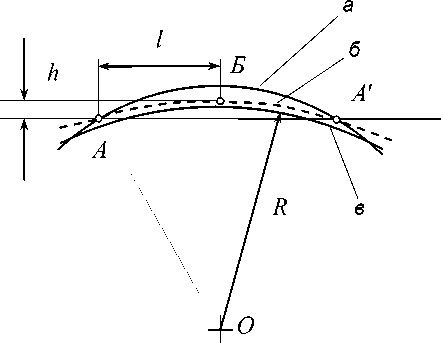
Рис. 1. Профиль рабочей поверхности рельса: а – стандартный; б - изношенный (уплощенный); в - восстановленный рельсошлифовани-ем; l - полуширина дорожки катания бандажа колеса по рельсу; h - высота сегмента дуги окружности профиля рельса

Измеряемые линейные размеры: высота сегмента дуги профиля рельса h и величина полуширины дорожки катания l . Расчетная формула радиуса шлифовки:

h 2 +12      D_h 12

R =        или R = 7 ⁺ 77 .   (2)

2h       22h

Непосредственно радиус кривизны профиля рельса R измерить нельзя, поэтому он определяется в результате косвенных измерений по прямым совокупным измерениям величин h и l . На рис. 2 приведена схема измерений.

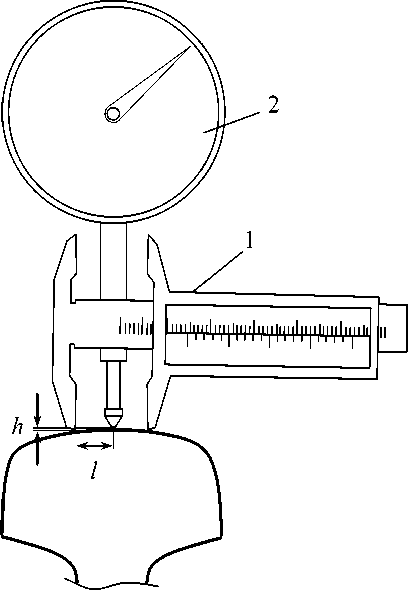
Рис. 2. Схема измерений: 1 – штангенциркуль; 2 – индикатор, закрепленный на неподвижной части штангенциркуля

Для измерений вначале определяются точки А и А ' границ пятна контакта «колесо-рельс» (рис. 3, а ), а затем измеряются высота и полуширина сегмента круга внутри этих границ. Очевидно, что из-за неравномерности износа рельса эти точки слегка «размыты» – могут смещаться относительно оси симметрии рельса случайным образом. Особенно эти смещения заметны вблизи стыков рельсов, как это видно из фото дорожки катания бандажа колес по рельсу – рис. 3, б .

Из рис. 3, а видно, что дорожка катания на выездной траншее располагается по центральной оси головки рельса. Из-за размытости точек возникают случайные погрешности измерений h и l, ко- торые в свою очередь обусловливают случайную погрешность радиуса R. Легко видеть, что точность измерения l оказы- вается    меньше,    чем точность измерения h.

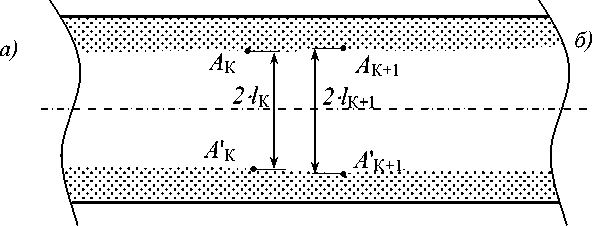
Рис. 3. Вид сверху на дорожку катания участка рельса – а ; фото дорожки катания бандажа колес по рельсу – б

Практические решения и рекомендации

Рассмотрим задачу определения радиуса профиля рельса выездной траншеи «Разреза Бородинский» Красноярского отделения СУЭК. Длина траншеи составляет 7160 м, которая для производ- ства измерений была разбита на 12 ше-стьсотметровых участков. Схема разметки выездной траншеи показана на рис. 4.

Измерения проводились в начале каждого участке через один метр (на рис. 4 обозначены номера участков измерений: 1, 2, 3, …, 11). Результаты измерений приведены в табл. 1.

Рис. 4. Схема разметки выездной траншеи

Оценим методическую погрешность определения R, считая, что размытость отсутствует, а затем проанализируем результаты реальных измерений. Поскольку истинные значения h, l и R неизвестны, то примем математические ожидания этих величин h0, l0 и R0 в качестве их оценки, а Δh, Δl и ΔR – в качестве погрешностей. Из соотношения (2) с учетом очевидных     условий     l0 >> Al2 , h 0 >> A h2 и Rо >> hо получим:

R ±AR = R + -0- Al ± -A0- Ah 0            0 h0       2h02     .

Отсюда получается погрешность Δ R измерения радиуса кривизны с избытком Δ R + и с недостатком Δ R – , мм:

	A R+	= - A A l +	l 02	A h
		h 0	2 h 0 2
A R = j
	A R	= + l0- A l -	l 02	A h
		h 0	2 h 02

Например, при следующих значениях математических ожиданий h0 = 0,47 мм, l0 = 25,5 мм, R0 = 692 мм и погрешностях измерений Δh = 0,01 мм и Δl = 0,1 мм получим ΔR+ = 9,1 мм и ΔR– = –9,5 мм, или в процентах ΔR% = +1,3/–1,4. При тех же значениях h0, l0 и R0 , но при погрешностях Δh = 0,02 мм и Δl = 0,1 мм получим ΔR% = +3,4 / –3,5. В случае одинаковых погрешностей Ah = Al = 0,05 мм получается AR% = +10,2 / -10,3.

Простой анализ показывает, что в рамках принятой модели и без учета случайной составляющей погрешности измерений методическая ошибка измерения радиуса кривизны поверхности рельса не превысит 5 % при Ah < 0,025 мм и Al < 0,1 мм.

Выполним анализ реальных измерений. Задача состоит в том, чтобы по полученным экспериментально данным найти наилучшую оценку истинного значения радиуса R .

Таблица 1

Результаты измерений параметров рабочих поверхностей дорожки катания рельсов

№ участка	Расстояние от начала траншеи, м	Измеренная величина	Номер измеряемого участка рельса
			1	2	3	4	5	6	7	8	9	10	11
1	400	h	0,42	0,43	0,41	0,38	0,37	0,45	0,48	0,47	0,45	0,44	0,42
		l	26,0	25,8	25,5	25,0	24,6	22,4	20,0	22,0	24,8	25,0	25,9
2	1000	h	0,41	0,39	0,52	0,43	0,44	0,39	0,38	0,41	0,52	0,45	0,41
		l	26,0	25,0	24,0	24,5	24,8	25,5	25,9	25,9	27,0	26,8	25,8
3	1600	h	0,52	0,37	0,39	0,41	0,55	0,43	0,41	0,39	0,42	0,41	0,43
		l	27,0	25,5	25,9	26,0	27,0	25,1	26,0	25,5	25,5	26,0	25,8
4	2200	h	0,42	0,43	0,41	0,39	0,42	0,43	0,39	0,42	0,55	0,58	0,43
		l	25,2	25,0	24,2	25,0	25,9	25,8	25,3	25,5	26,5	26,5	26,0
5	2800	h	0,55	0,41	0,43	0,41	0,39	0,37	0,38	0,42	0,43	0,42	0,41
		l	27,0	26,0	25,9	26,0	25,5	25,9	25,5	25,8	26,0	25,2	26,0
6	3400	h	0,41	0,43	0,42	0,41	0,39	0,43	0,38	0,37	0,55	0,42	0,40
		l	25,5	25,8	26,0	25,8	26,0	25,5	25,2	25,8	26,5	26,0	26,0
7	4000	h	0,42	0,39	0,41	0,43	0,38	0,45	0,48	0,42	0,40	0,37	0,41
		l	26,0	25,8	25,5	25,0	25,4	22,4	20,0	24,1	25,0	25,8	25,9
8	4600	h	0,43	0,41	0,52	0,42	0,40	0,38	0,37	0,39	0,52	0,43	0,42
		l	26,0	25,5	23,5	24,5	25	25,5	26,0	25,8	27,0	25,9	26,0
9	5200	h	0,52	0,43	0,41	0,39	0,55	0,51	0,45	0,42	0,42	0,40	0,38
		l	27,0	25,7	25,8	25,9	27,0	27,0	26,0	25,4	25,5	26,0	25,3
10	5800	h	0,43	0,40	0,37	0,38	0,40	0,43	0,42	0,41	0,42	0,43	0,39
		l	25,2	25	24,8	24,6	24,3	24,0	24,5	25,0	24,8	24,5	24,7
11	6400	h	0,55	0,41	0,42	0,43	0,40	0,38	0,39	0,37	0,38	0,39	0,41
		l	27,0	25,3	25,9	26,0	25,8	25,9	25,5	26,0	25,7	25,9	26,0
12	7000	h	0,41	0,38	0,42	0,43	0,41	0,40	0,39	0,41	0,55	0,43	0,42
		l	25,5	26,0	25,9	25,8	26,0	25,5	24,0	25,0	26,5	25,5	25,9

Очевидно следующее приближение (см. рис. 1):

R = h + L . И = 1Г1) 12

2  2 h 2 h 2 V h )

Радиус кривизны определяется в результате косвенных измерений, когда приходится учитывать случайные по- грешности [21]. В этой связи для оценки результатов измерений определим дисперсию D(R). Косвенные измерения производятся по нелинейной функциональной зависимости (3), поэтому дисперсия для произведения двух функций оказывается равной [35]:

^D ( R ) = 1 ^D

¹ )     ^{1        1}

+ M h J  4    h

X

обходимо добавить еще одно слагаемое

[36]:

x D ( l ² ) + M ² ( l ² )

- ¹ M ²

Здесь математические

1 | M 2. h J ожидания

D (R )=

¹ D | ¹ | + ¹ M ^г

4 V h J 4

X

первого и второго сомножителей в фор-

мулу

M ( ¹

V h

равны соответственно

1     22

= — и M ( l ) = 1₀ . С учетом этого ^h 0                  ⁰

(и коэффициента ½) получим:

D (R ) = 1D | 1 v ’    4 V h

x D ( l ² ) + l _o ⁴

)     1  1

" l + iJ  4 ho

14

4 h o ^{1 0} =

—

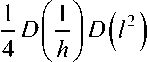
+ ¹ D

X

Здесь в последнем выражении можно пренебречь первым слагаемым, который не менее чем на порядок меньше ос-

тальных:

D (R) = 1D

Г 1 ) 14,1 n(,2\ 1

- lo +-D(l )-2. (6)

V h J 4 x ’ ho

Возникают некоторые проблемы с

О / О \ I Olli о о\ l2 + M2 l2  — M2 - M2 l2 +

’            J 4 V h J

+ ¹ Pi M | ¹ | MU ²) ID | ¹ | DU 2} 4 1 1² I h J   ^k        I h J ^k

h

Или с учетом (7):

D ( R ) = ^{l o}- D ( ¹ ) + D(l +

4 V h J h 52

0(9)

+2 ^T Pi h02

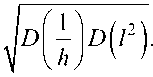
где px ;2 - коэффициент корреляции меж-h ду случайными погрешностями 1/h и l2.

Поскольку при вычислении R перемножаются l ² и 1/ h , то коэффициент корреляции между ними близок к коэффициенту корреляции между h и l ², взятому с противоположным знаком, потому что l ² возрастает, а 1/ h убывает. В результате из

формулы (9), с учетом условия

^P 1 1 2 h

определением первого слагаемого, поскольку измеряется h, а не обратная ей величина. Можно показать, что при вы- полнении

V D ( X ) <<  M ( X )

неравенства дисперсия оказыва- ется равна

D ( f ( X ) ) = ( f ( X ) I X = M ( X ) )² D ( X ) .(7)

Предполагая выполнение неравенств   TDh) << ho и DD(l2) << lo2   с учетом (7) получим из формулы (3): 42

D (R) = in'D(h)+D(l 2 )• 7o2. (8) 4h0                h0

Легко видеть, что определение дисперсии по формуле (8) оказывается несколько      проще      вычислений по формуле (6).

Следует учитывать, что измерения h и l выполняются одновременно, поэтому возможна корреляция между погрешностями их измерений и в формулу (4) не-

- 2 p получим:

D (R )=4^D (h)+D (12) t+

+ 2 p hl 2 ^^D ( ^h ) ^D ( ^{1 2} ) .

Соотношение (10) принимаем в качестве рабочего для определения оценок измерения радиуса.

Из анализа результатов измерений (табл. 1) легко увидеть недостатки эксперимента (ячейки выделены серым фоном). Исключая их, приведем результаты обработки данных в табл. 2.

В табл. 2 в строках R измеренных параметров приведен расчет радиуса по формуле (2) и по данным измерений h и l .

Конечно, из-за наличия погрешностей эти значения не являются истинными. Поэтому их можно оценить с помощью математического ожидания и среднего квадратичного отклонения:

R « M(R) ± TD(R). (11)

Таблица 2

Результаты обработки данных измерений

Участок	Измеренный параметр (Х)	M(X)	D(X)	V D ( X )	Phi 2	D(X)* по (9)	D(X)* D(X)	R		R
								R +	R –
400	h	0,42	7,71E-04	2,78E-02	0,285
	l	25,3	2,94E-01	5,42E-01
	R	775,7	2,63E+03	5,13E+01		2,79E+03	1,06	828,6	722,9	6,8%
1000	h	0,41	4,21E-04	2,05E-02	-0,534
	l	25,4	3,36E-01	5,80E-01
	R	796,3	4,22E+03	6,49E+01		4,45E+03	1,06	863,0	729,6	8,4%
1600	h	0,41	4,00E-04	2,00E-02	-0,147
	l	25,7	1,00E-01	3,16E-01
	R	814,2	2,10E+03	4,59E+01		2,23E+03	1,06	861,4	767,0	5,8%
2200	h	0,42	2,53E-04	1,59E-02	0,314
	l	25,3	3,17E-01	5,63E-01
	R	772,6	1,22E+03	3,50E+01		1,41E+03	1,16	810,2	735,0	4,9%
2800	h	0,41	4,23E-04	2,06E-02	0,535
	l	25,8	7,96E-02	2,82E-01
	R	818,5	1,84E+03	4,29E+01		1,23E+03	0,67	853,7	783,4	4,3%
3400	h	0,41	4,27E-04	2,07E-02	0,136
	l	25,8	7,60E-02	2,76E-01
	R	819,3	1,87E+03	4,32E+01		1,84E+03	0,98	862,2	776,5	5,2%
4000	h	0,40	4,00E-04	2,00E-02	-0,432
	l	25,4	3,69E-01	6,07E-01
	R	802,1	4,13E+03	6,42E+01		4,34E+03	1,05	868,0	736,2	8,2%
4600	h	0,41	4,78E-04	2,19E-02	-0,139
	l	25,6	2,74E-01	5,24E-01
	R	809,3	3,30E+03	5,74E+01		3,38E+03	1,03	867,5	751,2	7,2%
5200	h	0,41	3,24E-04	1,80E-02	-0,030
	l	25,7	6,95E-02	2,64E-01
	R	810,1	1,60E+03	3,99E+01		1,59E+03	1,00	849,9	770,2	4,9%
5800	h	0,41	4,42E-04	2,10E-02	-0,113
	l	24,7	1,18E-01	3,44E-01
	R	749,7	2,19E+03	4,68E+01		2,10E+03	0,96	795,5	703,8	6,1%
6400	h	0,40	3,73E-04	1,93E-02	-0,020
	l	25,8	5,56E-02	2,36E-01
	R	838,3	1,88E+03	4,34E+01		1,91E+03	1,01	881,9	794,6	5,2%
7000	h	0,41	2,67E-04	1,63E-02	0,314
	l	25,5	3,79E-01	6,15E-01
	R	795,0	1,82E+03	4,26E+01		2,47E+03	1,36	844,6	745,3	6,2%

Рассчитанные по этому соотношению радиус и его погрешность приведены в последних столбцах R , R ₊ , R _- и A R . Как видно, погрешность не превышает 8,5 %.

Полученные результаты (110 измерений) для радиуса кривизны рельса имеют распределение, близкое к нормальному. Гипотеза о нормальном распределении генеральной совокупности принимается по критерию Пирсона при уровне значимости 0,05. Исправленное среднеквадратическое отклонение этого набора данных составляет s = 51,87 [23]. Для построения интервальной оценки среднеквадратического отклонения генеральной совокупности воспользуемся известной формулой [23]:

s (1- q ) < о <  s (1+ q ).

Число s нужно брать из табл. [22], для количества измерений n = 110 и уровня значимости 0,05 оно приближенно равно 0,14. Таким образом, интервальная оценка для о принимает вид

44,61 < о < 59,13.

Проведем теперь интервальное оценивание математического ожидания генеральной совокупности в предположении, что она распределена нормально.

Среднеквадратическое отклонение генеральной совокупности заранее неизвестно, однако количество измерений больше 50, и в этом случае можно использовать в качестве среднеквадратического отклонения полученную величину s = 51,87.

Формула для интервальной оценки математического ожидания имеет вид [22]:

Rb - -^ < Ц < Rb + "^=. nт

мем равной 0,95. С помощью таблиц нормального распределения [36] находим t = 1,96. В итоге получаем 790 , 2 <  ц <  809 , 6 .

Заметим, что для симметричного интервала фиксирована величина

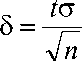
- полуширина доверительного

интервала, фактически ошибка оценивания. В нашем случае 5 = 0,187о, что является очень хорошей точностью оценки.

, 2^2

t G

Выражая n — 2 , получаем известную формулу для нахождения числа измерений, необходимых для достижения требуемой точности оценки.

Однако в условиях решаемой задачи, возможно, в применении этой формулы нет существенной необходимости. Полученная точность приемлема, а для ее увеличения, скажем, в два раза потребовалось бы увеличить число измерений в 4 раза, т.е. выполнить 440 измерений, что

уже не представляется реальным в повседневной практике. Если ограничиться надёжностью 95 %, t = 1,96, можно предельно упростить формулы для точности оценки и количества измерений:

5 —

1,96 ст

n

n — 3,841

5/

. При неболь

шой точности число n невелико. Например, если потребовать точность о = 0,5 □, теоретически будет достаточно 16 измерений. Однако в связи с тем что профиль рельса изменен неравномерно и требует измерения в разных точках, разбросан-

ных по длине рельса, столь малое число измерений представляется недостаточно информативным. Для практики, учитывая недостаточное качество балластного ос-

Здесь R b — 799 , 9 - среднее значение по выборке, n = 110 - число измерений а

Y число t находится из условия ^фО ) — —,

Y - надёжность оценки, которую мы при-

нования карьерных рельсов, для достоверности результатов измерений следует взять в 2–2,5 раза больше точек измерений, например, выполнять измерения в 36 точках.

Заключение

Предложена методика косвенных измерений для определения радиуса кри-

визны профиля рабочей поверхности рельса для обеспечения конформного контакта бандажа колеса локомотива с рельсом.

Установлено, что в связи с наличием случайных факторов, влияющих на ширину дорожки катания бандажа колеса локомотива с рельсом, следует исключить из полученных результатов случайные составляющие погрешностей измерений аргументов функции косвенных измерений.

В результате теоретических исследований получена упрощенная формула определения дисперсии функции косвенных измерений.

По данным измерений построены доверительные интервалы для оценки математического ожидания и среднеквадратического отклонения радиуса кривизны рельса. Рассмотрен вопрос о выборе числа измерений для достижения заданный точности оценки радиуса рельса.