Методика обеспечения полёта автоматических космических аппаратов «Ямал» синергетическим ресурсом рабочего тела электроракетных двигателей

24 ноября 2023 г. исполнилось 20 лет эксплуатации на геостационарной орбите автоматического космического аппарата (АКА) «Ямал-200» № 2. Одним из факторов, позволивших осуществить столь продолжительный полёт, является эффективное использование на борту АКА серии «Ямал» запасов рабочего тела (РТ). При этом критерием эффективности стала минимизация расхода РТ на выполнение программы полёта (ПП).

Традиционно управление расходом РТ на борту АКА связывают с работой электроракетных двигателей (ЭРД), являющихся, наряду с электродвигателями-маховиками (ЭДМ), исполнительными органами системы управления движением и навигации (СУДН). При этом процессы, протекающие в других системах аппаратов, рассматриваются как обеспечивающие при получении номинальных параметров тяги ЭРД.

При управлении АКА «Ямал» был впервые применён когнитивно-вариабельный синергетический¹ подход к решению задачи эффективного использования РТ. Отличительной особенностью предлагаемого подхода является то, что управление расходом РТ рассматривается как составная часть всего непрерывного сложного динамического процесса управления полётом аппарата с учётом возмущающего воздействия внешней среды и «неклонируемости» элементов систем. В определённой степени расход РТ зависит от синергетических явлений, происходящих в процессах систем: объединённой двигательной установки, энергоснабжения, обеспечения тепловых режимов, ориентации солнечных батарей (СБ), бортовых цифровых вычислений, управления бортовой аппаратурой, СУДН, — а также от алгоритмов управления этими системами, реализуемых в бортовом комплексе управления [1]. Таким образом, при управлении ресурсом РТ АКА рассматривается как единая синергетическая динамическая система, обладающая двумя фундаментальными свойствами:

• 1)    осуществлением обмена как с внешней средой, так и между подсистемами (системами АКА), энергией, веществом и информацией;

• 2)    взаимодействием, т. е. когерентностью, подсистем [2].

При этом эффективное управление расходом РТ — это не только уменьшение расхода за счёт выбора оптимальных режимов работы ракетных двигателей (РД), но и безрас-ходное управление при выполнении динамических операций. В рамках эффективного управления расходом РТ при выключенных РД выполняется безрасходное управление движением АКА с использованием внешних сил и моментов.

Постоянные синергетические наблюдения за герметичностью средств хранения и подачи РТ объединённой двигательной установки для предотвращения малых утечек из ёмкостей также относятся к проактивно-синергетическим методам управления бортовыми системами (БС), обеспечивающим эффективное расходование РТ [3].

Кроме того, до включения РД в БС выбираются начальные условия состояния борта, при которых обеспечиваются условия эффективного расхода РТ в РД [1].

В процессе работы РД, за счёт силы тяги двигателей, участвующих в коррекции орбиты, решается задача обеспечения начальных условий по суммарному вектору кинетического момента аппарата в конце манёвра для безрасходного управления движением АКА при последующем поддержании орбитальной ориентации с использованием ЭДМ.

Единым показателем максимальной эффективности применяемых методов синергетического управления БС является минимизация общих затрат РТ при выполнении номинальной ПП. При этом эффективность оценивается с учётом произошедших нештатных ситуаций в системе электроракет-ных двигателей (СЭРД), приводящих к невозможности использования в динамических режимах АКА части тяговых модулей, состоящих из ЭРД в виде стационарных плазменных двигателей (СПД) и блоков газораспределения.

В статье приводится обзор основных объединённых общим подходом методов управления движением центра масс и относительно центра масс АКА, составляющих методику обеспечения полёта аппаратов синергетическим ресурсом РТ. Синергетический ресурс РТ относится к виду сохранённых (оставленных) при выполнении одних и тех же технологических операций в БС, связанных с управлением движением центра масс и относительно центра масс АКА.

Основные принципы управления движением АКА «Ямал» и модификации алгоритмов в процессе полёта

СУДН построена по принципу корректируемой бесплатформенной инерциальной системы. Инерциальные датчики СУДН — высокоточные гироскопические измерители вектора угловой скорости. Выставка и коррекция бесплатформенной инерциальной системы осуществляется с помощью оптических датчиков [4].

Для управления ориентацией используется система из четырёх ЭДМ с кинетическим моментом 18 Н∙м∙с каждый. Разгрузка накопленного кинетического момента маховиков проводилась с использованием ЭРД в основном варианте, и с использованием ГД — в резервном.

Проведение манёвров осуществлялось с использованием восьми ЭРД. Далее в тексте вместо термина «ЭРД» используется термин «тяговый модуль» (ТМ). Каждый ТМ создаёт управляющий момент вокруг центра масс. Переключением отдельных ТМ в процессе коррекции орбиты обеспечиваются [5]:

• •    исключение расхода топлива на стабилизацию с использованием ТМ и системы маховиков за счёт одновременного управления движением центра масс и вокруг него;

• •    сокращение расхода на разгрузку накопленного кинетического момента маховиков между коррекциями орбиты за счёт частичного или полного сброса кинетического момента во время проведения коррекций орбиты.

Для парирования нерасчётных нештатных ситуаций, возникавших в полётах АКА «Ямал», были разработаны дополнительные алгоритмы управления, решавшие следующие задачи:

• •    разгрузку накопленного кинетического момента маховиков с использованием сил светового давления, осуществляемую путём поворотов СБ на допустимые (с точки зрения энергообеспечения АКА) углы;

• •    приведение кинетического момента маховиков к заданному значению с использованием моментов сил светового давления для реализации манёвров с использованием двух ТМ (в штатном варианте использовались четыре ТМ);

• •    управление движением центра масс с использованием сил светового давления;

• •    управление ориентацией АКА в прогнозе без измерений инерциальных и оптических датчиков с использованием гиросиловой стабилизации [6, 7].

Метод выбора варианта управления, оптимального по расходу рабочего тела, при коррекции орбиты аппарата с использованием тяговых модулей

В исправном состоянии СЭРД АКА «Ямал» обеспечивает n вариантов решения функциональной задачи — создания тягового усилия на АКА при проведении его манёвра на витке — с помощью восьми ТМ, разделённых на две группы (ТМ1, ТМ3, ТМ5, ТМ7 — 1-я группа; ТМ2, ТМ4, ТМ6, ТМ8 — 2-я группа), с переменным использованием двух катодов СПД-70 и двух комплектов блока автоматики управления (БАТМ) [8]. Любые изменения в выборе состава ТМ, катода СПД и комплекта БАТМ рассматриваются как наличие нового элемента множества вариантов N = {1... n } проведения манёвра. При этом множество объединяет два подмножества N ₁ и N ₂, принадлежащие двум баллистическим точкам прицеливания при проведении манёвра на витке:

N = N 1 U N 2 = { n | n e N 1 v n e N 2 } .

Проекции номинальных значений векторов тяги и управляющих моментов ТМ в связанной системе координат (ССК) АКА «Ямал» представлены в табл 1.

Таблица 1

Проекции векторов тяги тяговых модулей (ТМ) и создаваемых ими моментов на оси связанной системы координат (ССК)

№ ТМ	Сила в ССК			Момент в ССК
	Оx	Оy	Оz	Оx	Оy	Оz
1	0	Р 2	Р 3	– М 1	– М 2	М 3
2	0	Р 2	Р 3	– М 1	М 2	– М 3
3	0	– Р 2	Р 3	М 1	– М 2	– М 3
4	0	– Р 2	Р 3	М 1	М 2	М 3
5	0	– Р 2	– Р 3	– М 1	М 2	– М 3
6	0	– Р 2	– Р 3	– М 1	– М 2	М 3
7	0	Р 2	– Р 3	М 1	М 2	М 3
8	0	Р 2	– Р 3	М 1	– М 2	– М 3

Примечание. P ₂ , P ₃ — модули проекций тяги на оси Oy , Oz соответственно; М ₁ , М ₂ , М ₃ — модули проекций моментов, создаваемых каждым ТМ, на оси Ox , Oy , Oz соответственно. P ₂ = 0,0265 H; P ₃ = 0,0289 H; M ₁ = 0,01183 Н∙м; M ₂ = 0,00237 Н∙м; M ₃ = 0,00217 Н∙м.

Постановка задачи: произвести приоритетную расстановку n вариантов работы ТМ в СЭРД по расходу РТ в СПД как с учётом отдельных уникальных свойств элементов системы («неклонируемости»), так и системных свойств в целом, для получения минимальных затрат РТ ∆ G _{1 min} при проведении заданной коррекции орбиты АКА с использованием ТМ.

Для решения задачи в СЭРД при каждом i -м включении ТМ, где i — количество включений ТМ на типовом манёвре, i = 1, 2, …, 5, устанавливается суммарный массовый расход (в аноде и катоде) m ^. _∑ и удельный импульс тяги J_i по электродинамическим параметрам СПД и значению вектора тяги | F ^→ _i | [9]:

m ^. _{∑ i} = 1,1| F_i |² / [2αηcos²β( U _р – U _к) I _р] _i ;    (1)

Ji = | Fi | / –m. ∑i, где α — коэффициент, определяющий степень ионизации атомов ксенона; η — тяговый КПД СПД; cos β — значение осреднённого косинуса угла расходимости ионного потока из анодного пространства СПД; Uр — напряжение разряда СПД; Uк — прикатод-ное падение напряжения; Iр — ток разряда СПД; –m. ∑ — среднее значение суммарного секундного массового расхода топлива i-го варианта работающего ТМ, включающего расход через анод и катод СПД.

Значения U _к, η и cos β фиксируются при наземных проверочных испытаниях и заносятся в паспорта каждого ТМ. Значения электродинамических параметров — разрядного тока и напряжения — обеспечиваются работой выбранного комплекта БАТМ.

В процессе выработки ресурса СПД происходит разрушение его анодного блока (рис. 1), которое приводит к увеличению секундного массового расхода РТ через анод m ^. _аi .

В результате происходит постепенное увеличение (до ~33% при предельной огневой наработке продолжительностью 9000 ч — табл. 2) с отклонением от номинального значения силы тяги F ≈ 40·10^–3 Н [8, 10].

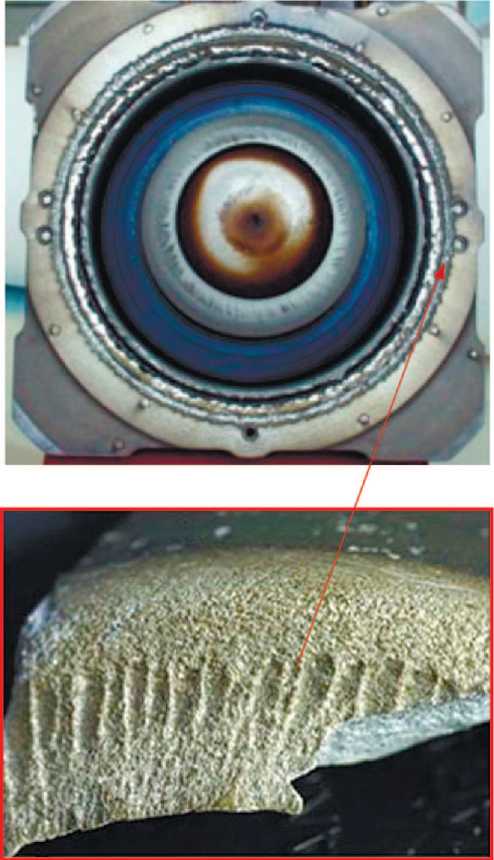
Рис. 1. Эрозия (изменение радиуса) на срезе керамической разрядной камеры электроракетного СПД-70 после огневой работы в течение 9 000 ч [11]

Таблица 2

Изменения основных параметров двигателя СПД-70 в процессе огневой выработки ресурса тягового модуля

Параметр	Наработка
	90 ч	9 000 ч
U р , В	315	285
U к , В	14	18
I р , А	2,33	2,13
α	0,96	0,95
cos β	0,98	0,95
η	0,51	0,50
m.а , кг∙ 10–6	2,67	3,61

Поскольку в процессе полёта АКА двигатели и комплекты БАТМ неравномерно вырабатывают свой ресурс [8], то целесообразно для манёвра выбирать группы ТМ с максимальным удельным импульсом тяги на момент начала текущего манёвра.

Метод включает в себя следующие действия:

• •    опред _→ еление значения тяги каждого ТМ | F_i | по результатам изменения характеристической скорости АКА до и после манёвра по данным радиоконтроля орбиты [12];

• •    измерение значения разрядного напряжения U _р и тока I _р в СПД каждого ТМ на манёвре;

• •    определение по электродинамическим параметрам суммарных, секундных массовых расходов РТ в каждом ТМ;

• •    выбор ТМ на манёвр по приоритету максимального удельного импульса тяги СПД.

При этом векторы тяги ТМ расположены под углом к осям связанного базиса. Новизна применения заключается в учёте месторасположения модулей на конструкции аппарата при определении вектора тяги [13, 14]. Для коррекции орбиты выбираются n вариантов ТМ из условия достижения ∆ G _{1 n min} на манёвре [10]:

∆ G _{1 n min} → ∑ J_i ( I _р, U _р) _n → max, i = 1, 2, …, 5 ;

i

∆ G = ∑ ^– m^.  ∆ t ,

1n       i     ∑ni    ni где Ji(Iр, Uр)n — значения удельных импульсов тяги СПД i-х ТМ в n вариантах коррекции орбиты [см. формулы (1)]; ∆tni — интервалы работы i-х ТМ в n вариантах.

При поиске оптимального варианта применялся метод комбинаторного анализа [15], который из конечного числа n вариантов выбора ТМ для коррекции орбиты позволял выбрать тот, при котором для получения одной и той же характеристической скорости аппарата расходуется наименьшее количество РТ. Для оценки расхода РТ одновременно учитывались действующие на АКА внешние возмущающие моменты, ограничения области располагаемых значений вектора кинетического момента в системе ЭДМ, значения проекций векторов тяги в заданном направлении коррекции орбиты, начальные значения суммарного вектора кинетического момента АКА, удельные импульсы тяги ТМ, работа БАТМ СЭРД [6, 7, 9, 10].

Методы оптимальной разгрузки электродвигателей-маховиков от накопленного кинетического момента с использованием реактивных двигателей

В общем случае расход массы рабочего тела ∆ G на разгрузку системы ЭДМ от накопленного кинетического момента c помощью РД определяется по следующему выражению:

∆ G j = ∑ ∆ K j / k mj ,                       (2)

j где ∆Kj, j = x, y, z — проекции вектора суммарного кинетического момента АКА ∆ K → на оси ССК, определённые для разгрузки ЭДМ; kmj — коэффициенты эффективности разгрузочного момента РД, kmj = Jdjldj, где Jdj — удельный импульс тяги РД; ldj — плечо действия силы тяги; d = 1, 2, …, 8 для ТМ (см. табл. 1) и d′ = 11, 12, …, 16, 21, 22, …, 26 для ГД с тягой FГД ≈ 0,1...0,5 Н (табл. 3).

Таблица 3

Проекции векторов силы тяги газовых двигателей (ГД) F _{ГД x} , F _{ГД y} , F _{ГД z} и создаваемых ими моментов М _{ГД x} , М _{ГД y} , М _{ГД z} на оси связанной системы координат

Двигатели		ГД x	ГД y	ГД z	М ГД
о о у =5	ГД11	0,7071	–0,7071	0	+ М ГД z
	ГД12	0,7071	0	–0,7071	– М ГД y
	ГД13	0,7071	0,7071	0	– М ГД z
	ГД14	0,7071	0	0,7071	+ М ГД y
	ГД15	0	1	0	+ М ГД x
	ГД16	0	–1	0	– М ГД x
О о у эЯ	ГД21	0,7071	–0,7071	0	+ М ГД z
	ГД22	0,7071	0	–0,7071	– М ГД y
	ГД23	0,7071	0,7071	0	– М ГД z
	ГД24	0,7071	0	0,7071	+ М ГД y
	ГД25	0	1	0	+ М ГД x
	ГД26	0	–1	0	– М ГД x

Примечание. F _{ГД x} , F _{ГД y} , F _{ГД z} — проекции единичных векторов тяги ГД на оси Oх , Oy , Oz соответственно; М _{ГД x} , М _{ГД y} , М _{ГД z} — модули проекций моментов, создаваемых каждым ГД, на оси Ox , Oy , Oz соответственно. Данные значения для тяги, равной 0,3 Н, составляют: М _{ГД x} = 0,216 Н∙м; М _{ГД y} = 0,366 Н∙м; М _{ГД z} = 0,456 Н∙м.

Оптимальность разгрузки обеспечивается за счёт определения при поддержании ориентации АКА динамических параметров, соответствующих наиболее эффективному применению РД с максимальными коэффициентами k_{mj max} для разгрузки ЭДМ от постоянной составляющей суммарн _→ ого вектора кинетического момента ∆ K в плоскости орбиты [см. формулу (2)] [16].

Сброс накопленного кинетического момента маховиков проводится с использованием ТМ и совмещается с проведением коррекций орбиты. Если коррекции орбиты по программе полёта не предусматриваются, то разгрузки приоритетно проводятся с использованием ТМ. Накопление кинетического момента за счёт действия моментов внешних сил происходит в основном в плоскости орбиты и составляет ~1 Н∙м∙с за виток (для АКА «Ямал-200»). Моменты, создаваемые ТМ по оси Ox , приблизительно в пять раз превышают моменты, создаваемые по осям Oy , Oz . Для минимизации расхода топлива разгрузки проводятся в моменты времени, когда ось Ox АКА в орбитальной системе координат совмещается с направлением сбрасываемого кинетического момента.

На рис. 2, 3 приводятся примеры сброса накопленного кинетического момента в плоскости орбиты. Осуществлялся сброс накопленного кинетического момента на величину | ∆Kх min | ≈ 3,9 Н⋅м⋅с. Оптимизация расхода РТ на разгрузку ЭДМ с использованием ТМ заключалась в выборе значения ∆Kmin и момента времени, когда создавался максимальный разгрузочный момент от силы тяги ТМ, направленный противоположно накопленному. Такой момент создавали пары из ТМ3 + ТМ7 и ТМ5 + ТМ1 для разгрузки ЭДМ относительно осей –Оx (рис. 2) и +Оx (рис. 3) соответственно. Время на одну разгрузку составляло ∼300 с, расход РТ составил ~0,37 г.

Разгрузка с использованием ГД решается как задача линейного программирования [15] с минимизацией расхода топлива.

На графике рис. 4 показан режим разгрузки ЭДМ от накопленного кинетического момента с использованием ГД по оси Оz .

Из рис. 4 легко определить постоянную составляющую суммарного вектора кинетического момента по углу наклона графика. Она составляла ~1,2 Н⋅м⋅с в сутки. Отрезок полётного времени [ t ₀, t_{s 0}], до «насыщения» системы ЭДМ по кинетическому моменту, рассчитанный с момента времени t ₀ с K_z = 0, при располагаемом значении вектора кинетического момента в системе маховиков по оси Oz K_sz = 16 Н·м·с, составляет ~13 сут.

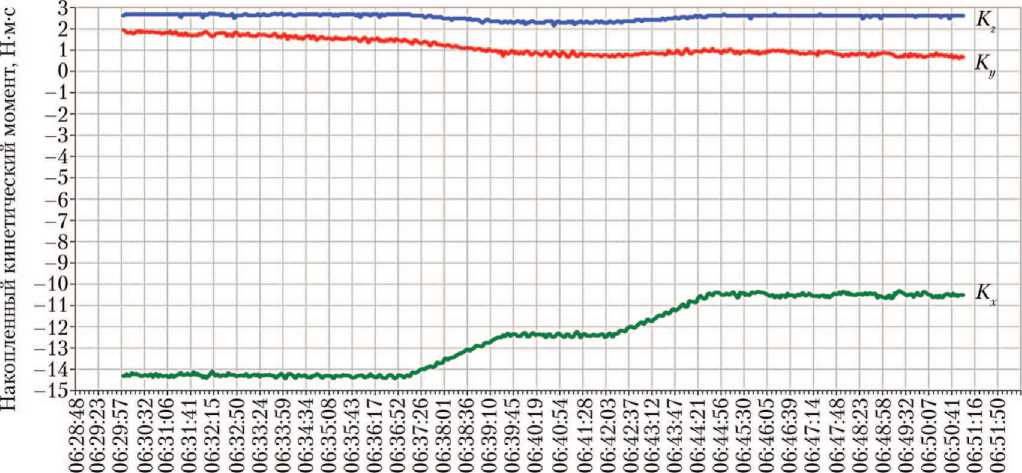
Время, чч:мм:сс

Рис. 2. Графики разгрузки накопленного кинетического момента в электродвигателе-маховике по оси –Оx связанной системы координат (ССК) с использованием пары тяговых модулей ТМ3 (М₁, –М₂, –М₃) и ТМ7 (М₁, М₂, М₃) (см. табл. 1): K_x, K_y, K_z — проекции вектора суммарного кинетического момента автоматического космического аппарата на оси ССК (рисунок создан авторами)

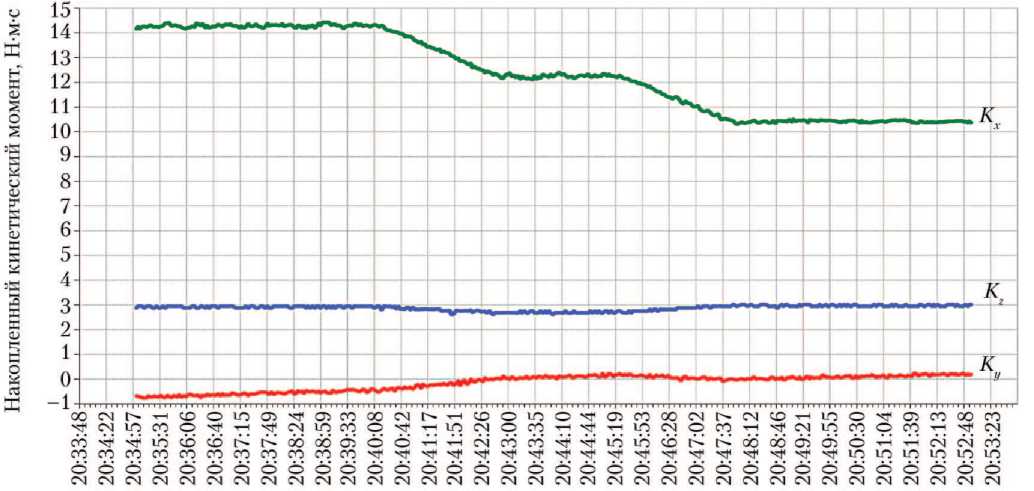
Время, чч:мм:сс

Рис. 3. Графики разгрузки накопленного кинетического момента в электродвигателе-маховике по оси +Оx связанной системы координат (ССК) с использованием пары тяговых модулей ТМ5 (–М1, М2, –М3) и ТМ1 (–М1, –М2, М3)

(см. табл. 1): K_x, K_y, K_z — проекции вектора суммарного кинетического момента автоматического космического аппарата на оси ССК (рисунок создан авторами)

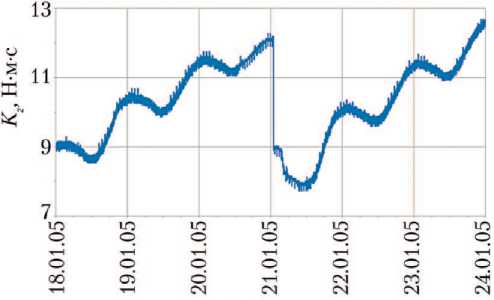
Дата

Рис. 4. График разгрузки электродвигателя-маховика от накопленного кинетического момента K_z по оси Оz связанной системы координат с использованием газового двигателя (рисунок создан авторами)

∆ G_{j 2 min} → ∆ K_j → min; ∑ k_mj → max; j = 1, 2, …, 12 ; j

• ^{∆ G}j 2 ⁼ ∑^{∆ K}j min ^{/ k}mj max^. j

Метод проведения разгрузки маховиков при коррекции орбиты космического аппарата тяговыми модулями

Разгрузка накопленного кинетического момента маховиков, совмещённая с коррекцией орбиты АКА, при использовании ТМ, векторы тяг которых расположены под углом к осям связанного базиса, проводится без расхода РТ на управление

Для разгрузки подходят ГД13 и ГД23 (см. табл. 3). Проведена оценка k_{m 13 max} и k_{m 23 max} через среднестатистический расход РТ при проведении аналогичных разгрузок на АКА «Ямал-200» № 2. Для ГД13 расход составил ∼ 1,16 г на

1 Н⋅м⋅с, а для ГД23 — ∼1,28 г на 1 Н⋅м⋅с, что соответствует km13 max ≈ 0,86 м2⋅с–1   и k m23 max

В более РТ с

≈ 0,786 м2⋅с–1.

данном случае разгрузку ЭДМ выгодно проводить по расходу использованием ГД13. В мето- дах разгрузки ЭДМ от накопленного кинетического момента с использованием РД реализуется следующее условие выполнения оптимальной разгрузки:

движением относительно центра масс. Затраты РТ учитывались на достижение требуемого значения характеристической скорости аппарата [17]. В конце коррекции орбиты ( t _к) при помощи управляющих моментов ТМ формируется суммарный кинетический момент K ^→ ( t _к) = H ^→ ( t _к) + J ω ^→ _o, где J — тензор инерции АКА; ^→ ω_o — орбитальная скорость, для которого выполняется следующее условие:

→

K (tк) ∈ S′; S′⊆ S, где S′ — подобласть, принадлежащая области S располагаемых значений вектора кинетического момента системы

ЭДМ H ( t ), обеспечивающая безрасходное поддержание (без разгрузки с использованием реактивных двигателей) орбитальной ориентации АКА маховиками на интервале между коррекциями орбиты (рис. 5).

Путём прогноза изменения вектора кинетического момента в процессе проведения манёвра выбирались пары ТМ, обеспечивающие получение начальных условий для последующего поддержания ориентации без включения РД на разгрузку от накопленного кинетического момента (рис. 6).

На рис. 6 приведены графики изменения суммарного кинетического момента системы маховиков при проведении манёвра. Видно, что по окончании манёвра суммарный кинетический момент не превышает 60% от максимально возможного.

На АКА «Ямал» ТМ расположены таким образом, что векторы тяги находятся в двух плоскостях, перпендикулярных оси Оx , а центр масс находится в начале ССК. За счёт выбора ТМ из двух разных групп приведение кинетического момента к заданному значению осуществлялось сразу по трём осям — Ох , Оy и Оz .

Из-за нештатной ситуации, произошедшей в БАТМ АКА «Ямал-100» [10], выполнение манёвров с использованием ТМ второй группы стало невозможным. В таком случае провести необходимое приведение кинетического момента к заданному значению в конце манёвра только на одной, первой группе ТМ по оси Оz стало также невозможным. Для дальнейшего выполнения ПП необходимо было проводить дополнительную периодическую разгрузку ЭДМ от накопленного кинетического момента по указанной оси с использованием ГД, что не является целесообразным с точки зрения эффективного использования РТ.

При этом реальное размещение ТМ относительно положения центра масс вносит определённые отклонения («синергетические возмущения») в процесс. На рис. 7 показаны графики изменения величин приращения кинетического момента по оси Оz в конце манёвров (∆ K_{zn ′}), полученные по результатам статистической обработки телеметрической информации для двух групп ТМ:

n ′ = 1 — 1-я группа, состоящая из ТМ1, ТМ3 и ∆ K_{z 1};

n ′ = 2 — 2-я группа, состоящая из ТМ5, ТМ7 и ∆ K_{z 2}.

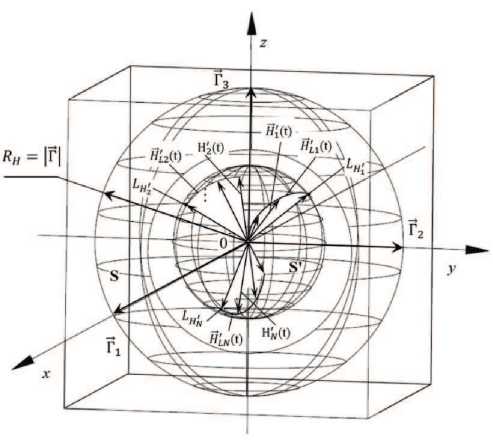
Рис. 5. Схема образа процесса приведения кинетического момента в системе электродвигателей-маховиков (ЭДМ) на манёвре в заданную подобласть S ′ : Оxyz — оси связанной системы координат автоматического космического аппарата; R_H — радиус вписанной сферы; S — область располагающих значений кинетического момента системы

→→→ ЭДМ; Г ₁ , Г ₂ , Г ₃ →→ H ₁ ′ (t), H ₂ ′ (t), …, ческого момента тяговых модулей

• — кинетические моменты ротора ЭДМ; H ^→ _N ′ (t) — изменения вектора кинети-системы ЭДМ при крайней работе на манёвре (1, 2, ..., N — варианты);

  H ^→ _L ′ ₁ (t), H ^→ _L ′ ₂ (t), …, H ^→ _L ′ _N(t) кинетического момента

  
  

изображающие точки вектора на поверхности области S ′ ;

L , L , …, L — фазовые траектории (линии годографа) H1    H2         HN вектора кинетического момента на поверхности области S′ (рисунок создан авторами)

Обе группы ТМ последовательно задействовались для коррекции орбиты АКА по наклонению с примерно одинаковой продолжительностью работы. Как видно из графиков рис. 7, 1-я группа «накапливала» отрицательное значение кинетического момента ∆ K_{z 1}, а вторая — положительные значения ∆ K_{z 2}. При этом отношение ∆ K_{z 2}/|∆ K_{z 1}| колеблется в среднем от 1,5 до 10 единиц. Есть также на графиках особые точки, где ∆ K_{z 2} и ∆ K_{z 1} — одного (положительного) знака.

Указанные цифры соответствует соотношению проводимых манёвров на разных группах ТМ. Например, при соотношении, равном ∼10, для компенсации ∆Kz2, полученного к концу манёвра на 2-й группе ТМ, необходимо провести ∼10 манёвров на 1-й группе и т. д. Поскольку одной группой ТМ, исходя из условий баллистики, можно проводить манёвр один раз в сутки, то, следовательно, может быть следующее суточное чередование манёвров: одни сутки — на 2-й и 1-й группе ТМ, далее девять суток — только на 1-й группе ТМ и т. д. Указанная схема приводит к неравномерной выработке ресурсов ТМ и неэффективному расходу РТ.

С целью выравнивания указанного соотношения и сокращения числа включений ГД для разгрузки ЭДМ, проводился переход от стихийного синергетического воздействия на процесс к направленному путём смещения центра масс АКА за счёт неравномерной выработки РТ из двух баллонов [8, 18].

Разработана общая методика выравнивания значений управляющих моментов, создаваемых неподвижно установленными ЭРД, векторы тяг которых направлены под углом к осям базиса, связанного с космическим аппаратом, за счёт направленного смещения его центра масс.

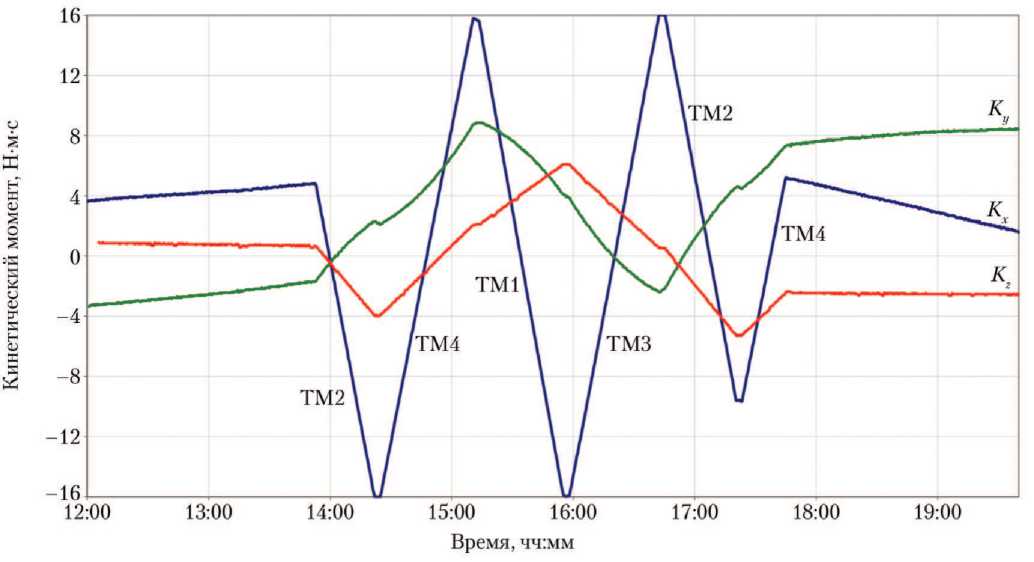
Рис. 6. Изменения компонент K_x, K_y, K_z суммарного кинетического момента при проведении манёвра автоматического космического аппарата «Ямал» на тяговых модулях ТМ2 → ТМ4 → ТМ1 → ТМ3 → ТМ2 → ТМ4 (рисунок создан авторами)

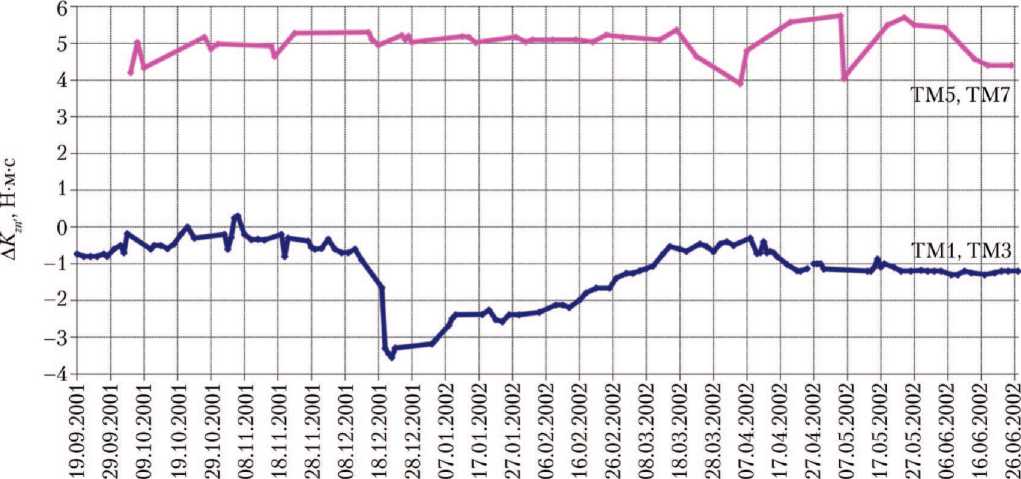
Дата, дд.мм:гпт

Рис. 7. Статистические данные по приращению кинетического момента по оси Оz K_{zn ′} автоматического космического аппарата «Ямал-100» в процессе манёвров на тяговых модулях 1-й группы (рисунок создан авторами)

Методы управления разгрузкой маховиков без расхода рабочего тела с использованием солнечных батарей

К оптимальным методам управления движением АКА относительно центра масс с решением задачи минимизации затрат РТ на выполнение динамических операций относится управление движением с использованием моментов, создаваемых внешними силами. Управление АКА осуществляется системой маховиков, а моменты, создаваемые внеш- ними силами, используются для разгрузки системы от накопленного кинетического момента. В качестве исполнительного органа управления моментами от внешних сил на АКА «Ямал» использовались поворотные СБ.

Общим для всех далее рассматриваемых методов разгрузки системы ЭДМ от накопленного кинетического момента с использованием СБ является выполнение условия разгрузки, сформулированного скалярным произведением m→ ∙ h < 0, где m→ — единичный вектор момента внешних сил, действующих на рабочую поверхность СБ; h — единичный вектор накопленного кинетического момента в системе ЭДМ.

В зависимости от природы внешних сил, методы подразделяются на:

• •    разгрузку с использованием моментов от сил светового давления [19]

L _с — расстояние от КА до Солнца; Е _с — плотность падающего солнечного излучения; с — скорость света;

• •    разгрузку с использованием вз _→ а-имодействия магнитных моментов L _м токовых контуров СБ с магнитным полем Земли (МПЗ) [20], где

m→ = ( L→м /| L→м|) × ( B→ /| B→|), где B — вектор индукции МПЗ.

Для формирования магнитного разгрузочного момента был разработан новый способ определения собственного магнитного момента СБ. Расчёт выполняется в моменты времени, когда АКА находится в режиме штатной орбитальной ориентации. Назначаются два интервала для измерения значений кинетического момента АКА. Первый интервал измерений выбирается на теневой, а второй — на освещённой Солнцем части орбиты. Математическая обработка разности значений накопленного кинетического момента позволяет выделить из главного м _→ омента внешних возмущающих сил M _м магнитный момент, который создали токовые контуры СБ при взаимодействии с МПЗ на освещённом интервале орбиты.

В процессе определения собственного магнитного момента СБ был определён порядок значений моментов внешних сил, действующих на АКА «Ямал».

Результаты расчётов представлены в табл. 4.

Таблица 4

→    →   →    →→ →

M s = ^→ r 1 × F c1 + ^→ r 2 × F c2 ;       m = M s / | M s |,

где ^→ r_i , i = 1, 2 — радиус-векторы центров светового _→ давления на поверхности СБ-1 и СБ-2; F _{c i} — сила, действующая на i -ю рабочую поверхность СБ-1 и СБ-2:

→ F c i

→→ ci погл       ci отр;

F c i погл = – ^→ e c [ s i (1– ρ i ) cosα i ( L З / L с )²( E с / c )];

F ^→ c i отр = – ^→ n i [2 s i ρ i cos²α i ( L З / L с )²( E с / c )], здесь ^→ e _c — единичный вектор направления на Солнце; ^→ n_i — нормаль к i -й рабочей поверхности СБ; s_i — площадь i -й рабочей поверхности i -й СБ; ρ _i — коэффициент зеркального отражения i -й СБ; α _i — угол между векторами ^→ n_i и ^→ e _c; L _З — расстояние от Земли до Солнца;

Порядок значений внешних возмущающих моментов, действующих на космические аппараты «Ямал» в процессе их эксплуатации на геостационарной орбите

Момент, Н∙м		Порядок значений
		По оси Oх ССК	По оси Oу ССК	По оси Oz ССК
О эЯ Я о S	Земли	10–24	10–8	10–6
	Солнца	10–12	10–13	10–11
	Луны	10–11...10–13	10–12...10–13	10–11...10–13
Магнитный		10–4...10–6	10–4...10–6	10–5...10–8
Сил светового давления		10–4...10–6	10–4...10–6	10–6...10–8
Суммарный		10–4...10–6	10–4...10–6	10–5...10–8

Как видно из табл. 4, основными являлись моменты сил светового давления, моменты от взаимодействия магнитного момента СБ с МПЗ. Именно эти две составляющие были использованы для разгрузки ЭДМ АКА «Ямал» от накопленного кинетического момента с использованием СБ.

Методы позволяют осуществлять разгрузку не только до нулевых, но и до заданных значений, обеспечивая тем самым необходимые начальные условия по вектору кинетического момента в ЭДМ перед проведением манёвра (см. рис. 6). Это позволило увеличить продолжительность работы первого включённого для проведения манёвра ТМ в ~1,6 раза. При этом был получен синергетический ресурс другого параметра — количества включений ТМ на манёврах.

Метод использования солнечных батарей для одновременного управления движением центра масс и относительно центра масс

Для коррекции орбиты геостационарного спутника связи «Ямал» по трансверсали с одновременной разгрузкой маховиков от накопленного кинетического момента без расхода РТ в качестве исполнительного органа использовались СБ [21]. При эт _→ ом проекции силы светового давления F_sd ( F_{sd x} , F_{sd y} , F_{sd z} ) на оси ССК Оxyz при одновременном развороте обеих батарей на угол a_СБ определялись из следующих уравнений:

F dx = — Р с S _СБcosa_c [т x (1 — р) cosa_СБ +

+2рт x cos³a_СБ - 2рт y cos²a_СБsina_СБ];

F dy = — Р с S _СБcosa_c [т y (1 — р) cosa_СБ +

+2рт y cos³a_СБ + 2рт x cos²a_СБsina_СБ];

Fsdz = — Рс S СБ(1 — Р)т z cosaccosaСБ, где Рс — давление солнечного света; SСБ — суммарная площадь СБ; р — коэффициент зеркального отражения; тx, тy, тz — проекции единичного вектора направления на Солнце в ССК; а = arccosw т2 + т2 — c      xy угол между направлением на Солнце →ec и плоскостью орбиты.

Проекци _→ и момента сил светового давления M _s ( M_sx , M_sy , M_sz ), определяемого в зависимости от положения СБ, при условии совпадения центра масс КА с центром светового давления, определялись из следующих уравнений [21]:

Mx = Рс S СБр R cos2acx х (-sina1cos2a1 + sina2 cos2a2 );

M y = Р с S _СБ R cos²a c x

1 – ρ

(cosa 1 - cosa₂) + p(cos³a 1 - cos³a₂)

где R = | r_i |, i = 1, 2 — радиус центров светового давления на поверхности СБ-1 и СБ-2; а 1 , а₂ — углы поворота СБ-1 и СБ-2 относительно положения, при котором нормаль n совпадает с проекцией вектора ^→ e _c на плоскость орбиты.

При этом уравнения записаны для инерциальной системы координат, совпадающей с ССК, когда проекция вектора ^→ e _c на плоскость орбиты противоположно направлена оси Ох ССК.

У проекции M_sz на ось Оz постоянная составляющая отсутствует, а развороты СБ на углы а₁, а₂, соответственно, приводят к появлению периодической составляющей

M sz = Р _с S _СБр L cos²a c x

x(sina1cos2a1 + sina2cos2a2), где L — расстояние от центра светового давления до центра масс АКА.

При развороте СБ-1 и СБ-2 на углы a 1 , a₂ ток прихода СБ I _СБ заведомо превышает ток нагрузки I _н с учётом предельно допустимого значения разницы тока прихода и тока нагрузки А I :

¹ СБ >  ¹ н ^{+ А 1} -

Решение задачи оптимизации по расходу РТ А G 3 max выполняется через максимизацию значений следующих скалярных произведений:

F d (a) • А V ^ max;

Ms(a1, a2) • K1 < 0; | Ms(a1, a2) • K11^ max, где AV — вектор требуемого измене-→ния характеристической скорости АКА; K1 — составляющая суммарного вектора кинетического момента АКА K в плоскости орбиты.

Экономия РТ на n-м витке определяется через сумму значений необходимых q-х разгрузок кинетического момента, которые выполнялись в системе ЭДМ без расхода РТ по j-м осям КА в плос- кости орбиты ( j = x, y)

∑∆K(q, j)n и q, j

полу-

ченной на n -м витке величины характеристической скорости ∆ V_{n τ} в направлении трансверсали.

При этом в соответствие каждому ∆K(q, j)n ставится ∆G(q, j)n оценки расхода РТ на выполнение разгрузки на n-м витке с оптимальным использованием РД, и каждому ∆Vnτ — значение ∆GVn оценки расхода РТ на выполнение манёвра с использованием РД при заданной величине характеристической скорости.

Таким образом, экономия РТ на n -м витке управления движением относительно центра масс и центра масс АКА составит

∆ G

( q , j ) n max

→

→ ∑ ∆ K

(q, j)n q, j

→ max; j = x , y ; ∆ V_{n τ} → max .

Солнечные батареи использовались для проведения трансверсальных манёвров АКА с использованием сил светового давления. При этом отрабатывалась величина характеристической скорости в год ~1 м/с.

Выводы

Применение методики когнитивновариабельного обеспечения синергетическим ресурсом РТ системы ТМ для АКА «Ямал-100», «Ямал-200» № 1 и 2, позволяло получать в год синергетический ресурс РТ от 500 до 800 г. Экономия определялась с учётом особенностей выполнения программы полёта.

За ~10 лет полёта синергетический ресурс РТ для АКА «Ямал-100» составил ~8,5 кг, а для «Ямал-200» № 1 — ~6,4 кг, при исходной заправке баллонов ~109 кг.

Синергетический ресурс для АКА «Ямал-200» № 2 по РТ на текущий момент составил ~12,5 кг при исходной заправке баллонов ~109 кг.

Рассмотренные методы, применяемые для получения синергетического ресурса РТ, являются универсальными и могут быть использованы при управлении динамическими режимами космических аппаратов, содержащих ЭДМ, ЭРД и ГД в качестве исполнительных органов системы управления движением.

При этом под полученным синергетическим ресурсом РТ понимается то его количество, которое необходимо было бы дополнительно израсходовать на выполнение аналогичной динамической части программы полёта АКА «Ямал» без применения рассмотренной методики.