Методика обоснования алгоритма обнаружения многоспектрального спонтанного излучения и оценки его эффективности

В ранее выполненных работах, в том числе с участием авторов [1–5], показано, что пред-генерационное спонтанное излучение характеризуется широким и весьма неравномерным спектром. При этом с использованием терминологии зонной теории следует отметить, что большие значения амплитуд спонтанных излучений соответствуют длинам волн переходов, связанных с накачкой, последующими переходами до и после метастабильного уровня. На рис. 1 представлены типовые нормированные осциллограммы излучения лазера на AUG с неполным резонатором при переходе из метастабильного уровня.

Как следует из рис. 1, спонтанные излучения будут характеризоваться и существенной нестационарностью, связанной с ростом основных спектральных составляющих спонтанных излучений с течением времени, от момента включения системы оптической накачки до момента времени включения высокой добротности резонатора. На указанном интервале времени будет располагаться предгенерационное спонтанное излучение, которое представляет интерес в части формирования упреждающих действий, а также определения состояния лазерного средства при раздельном сопоставительном анализе спектральных составляющих спонтанных излу- – 410 –

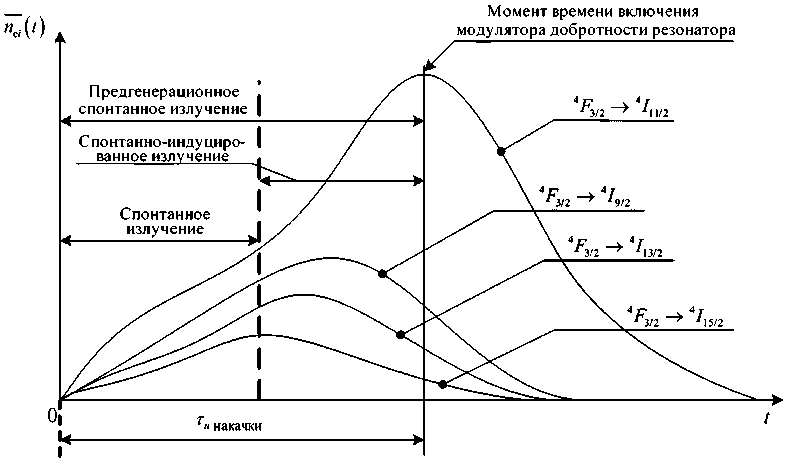
Рис. 1. Типовые осциллограммы изменения интенсивностей основных спонтанных излучений лазера на AUG во времени

Fig. 1. Typical oscillograms of changes in the intensities of the main spontaneous emissions of the AUG laser over time чений, с учетом закономерностей относительных изменений их во времени. Во всех случаях рассматриваемые спонтанные излучения представляются как полезные сигналы, прошедшие через атмосферный канал, аддитивно вносящий фоновое излучение, турбулентные искажения, аэрозольное и молекулярное ослабление как мультипликативные составляющие помехи. Кроме того, необходимо учесть шумы, исходящие от исследуемых лазерных средств, а также внутренние шумы.

В связи с этим целью настоящей статьи является обоснование рационального способа и алгоритма обнаружения совокупности спонтанных излучений, а также каждой составляющей в зависимости от дальности в типовых атмосферных условиях.

Описание процесса сигнального воздействия на вход многоканального приемника

Рассмотрим случай, когда каждая составляющая спонтанного излучения наблюдается в течение интервала времени TM , который допускает разбитие на M одинаковых подынтервалов длительностью τ_н так, что M τ_н = T_M .

Как показано в [3–7], в общем случае в течение длительности подынтервала τн интенсивность k -го спонтанно-индуцированного излучения в i -м подынтервале запишется в виде /Д^=Ё^;/ = й7)^.

Помеховая составляющая в каждом спектральном участке спонтанно-индуцированных излучений предполагается стационарной с постоянной интенсивностью γ ш k .

Решение принимается после последовательного накопления М отсчетов по каждому спектральному интервалу. В этом случае полагаем, что приемник в общем случае должен быть

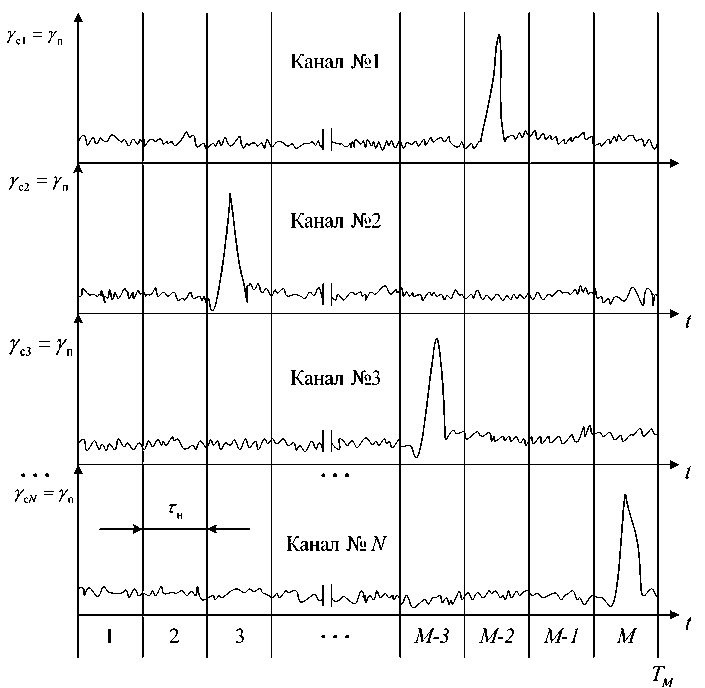
Рис. 2. Реализации входных воздействий поступающих на вход многоканальных приемников после частотного разделения

Fig. 2. Implementations of input signals arriving at the input of multichannel receivers after frequency division многоканальным (N каналов), при этом в каждом канале наблюдается реализация длительностью TM (рис. 2).

Для рассматриваемого случая, как показано в [7,8], в качестве оптимального приемника может рассматриваться приемник, работающий по правилу Неймана-Пирсона (с квантовым счетчиком в качестве чувствительного элемента).

При использовании указанного критерия выборка из реализации

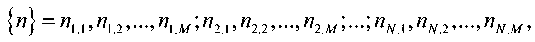
имеющаяся на входе приемника, отожествляется с наличием сигнала в том случае, если выполняется неравенство [6]

a \ =                ;

или отождествляется с наличием шума, если λk < λ0k, где МИ) – совместная плотность вероятности для совокупности выборочных значений {n}k в k-м канале при условии, что сигнал присутствует; МИ J – совместная плотность вероятности для той же совокупности выборочных значений в k-м канале при условии, что сигнала нет; λ0k – пороговая величина, которая выбирается так, чтобы вероятность выполнения неравенства λk ≥ λ0k, при отсутствии сигнала была равна фиксированному значению Fл.т..

Если выборочные значения статистически независимы, то многомерное отношение правдоподобно.

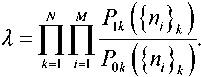
Как известно [7], критерии обнаружения удовлетворяющие другим условиям оптимальности, отличаются друг от друга лишь выбором величины λ ₀. Критерий обнаружения Неймана-Пирсона соответствует условиям, когда число отсчетов в выборке фиксировано. Анализ выборочных значений осуществляется в процессе их поступления.

Алгоритм работы оптимального приемника определяется λ , а следовательно, видом плотностей ММ) и ^>* ({ⁿi}k) ^.

В случае слабых спонтанных сигналов и помехового излучения справедливы соотношения:

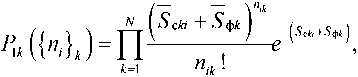
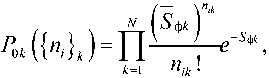
где S cki – среднее число сигнальных фотоэлектронов, вызванных воздействием на фотоприемник k -го спонтанно-индуцированного излучения за время i -го отсчета; S фк – среднее число шумовых фотоэлектронов в k -м спектральном канале за время i -го отсчета.

Обозначим ^^^ki ~ Ym^t ; $№ ~ Yw^T , где γ ф k – интенсивность потока шумовых фотоэлектронов.

Тогда, используя рекомендации, изложенные в [1], отношение правдоподобия и его логарифм при многоканальном обнаружении можно представить с помощью выражений:

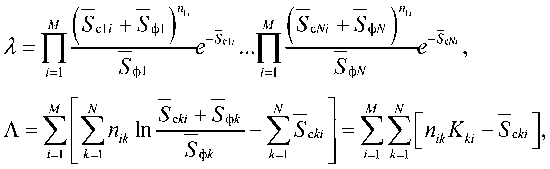
где^,=ln^   .

Структурная схема приемника, реализующая алгоритм, представленный выражением, будет иметь вид[1], изображенный на рис. 3.

Оптимальный обнаружитель (при использовании в приемнике N каналов, каждый из которых обеспечивает наилучшим образом преобразование спонтанно-индуцированного из- – 413 –

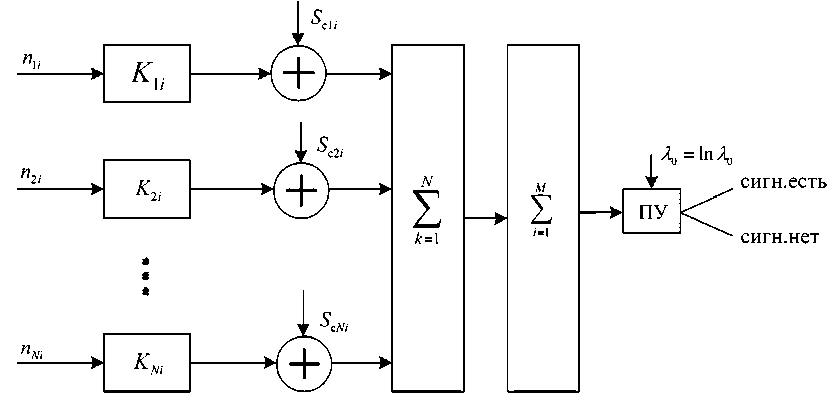
Рис. 3. Структурная схема оптимального приемника обнаружения спонтанно-индуцированного излучения

Fig. 3. Block diagram of an optimal receiver for detecting spontaneously induced emission лучения в электрический сигнал) синтезирован с частично заданной структурой, в качестве которой рассматриваются эквивалентные схемы фотоприемников. Приемник (с учетом электронной части) должен в каждом k-м канале суммировать выборочное значение ni(n1, n2,…, nm), умноженное на весовой коэффициент Kki, и вычесть из произведенного средних значений S cki . Образованная сумма поступает на пороговое устройство и сравнивается с порогом λ0 = lnλ0. Если сумма равна или превышает порог, принимается решение о присутствии в принятой смеси спонтанно-индуцированного излучения, в противном случае – об отсутствии в смеси искомого сигнала.

Приемник, осуществляющий решение на основании отношения правдоподобия, обладает наилучшей эффективностью и может служить в качестве стандарта для сравнения и выбора характеристик приемника [8].

Оценка эффективности алгоритма приема предгенерационного многоспектрального спонтанного излучения передающего лазерного канала

Оценим эффективность алгоритма, представленного выражением. Для этого в качестве показателей будем использовать условные вероятности обнаружения P _обн и ложных тревог F _л.т., для нахождения которых необходимо значение распределений вероятностей логарифма отношения правдоподобия Λ при наличии и отсутствии сигнала.

Обозначим fc (Λ) и f 0 (Λ) плотности вероятности величины Λ соответственно при наличии и отсутствии сигнала. В этом случае

^. = J Z(A)dA;                                        (8)

ло

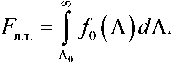
Нахождение плотностей fc (Λ) и f 0 (Λ) при произвольных отношениях сигнал/шум представляет большие трудности.

Плотность вероятности Λ при отсутствии и наличии искомых сигналов описывается вы- ражениями

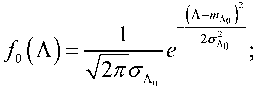
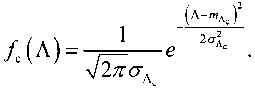
где m\ и

математическое ожидание и дисперсия суммы при отсутствии и наличии ло(с) ло(с)

сигнала.

где

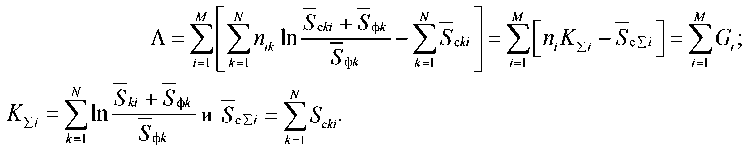
Полезный сигнал и помеха на входе имеют законы распределения Пуассона. Тогда распределения случайных величин n_ik будем считать известными (они определяются выражениями,), тогда легко найти математическое ожидание ^^ и дисперсию^-^■)²)функции этой случайной величины ^K^S^ при отсутствии и наличии сигнала.

Для первого канала

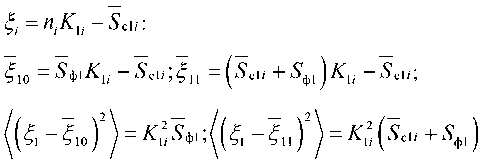
Поступая аналогично для остальных каналов, учитывая статистическую независимость слагаемых при суммировании по каналам i -го отсчета, находим:

;

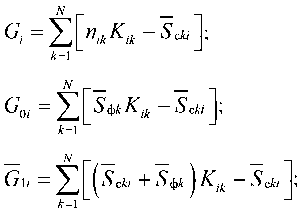
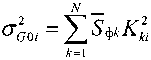
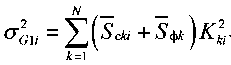
Учет суммирования по времени дает

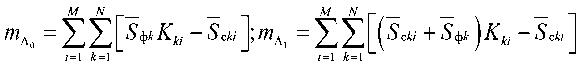
Л,

М N

м

Используя и, находим:

;

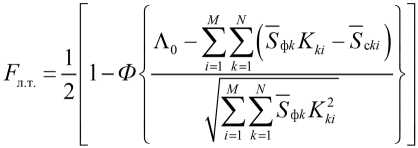
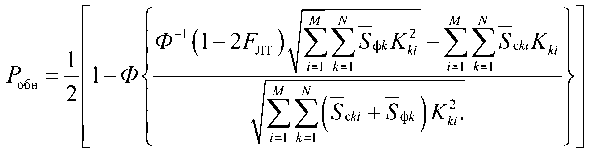
где N – количество каналов ( k ); M – количество отсчетов ( i ); Ф^х) =

2 л-

je ²dt ;

О

Ф '[ф(х)] = х.

В табл. 1 указаны значения S cki .

Среднее число шумовых фотоэлектронов в k -м спектральном канале за время i -го отсчета равно 3 ( S^k = 3).

Таблица 1. Значения среднего числа сигнальных фотоэлектронов, вызванных воздействием на фотоприемник k -го спонтанно-индуцированного излучения за время i -го отсчета

Table 1. Values of the average number of signal photoelectrons caused by the action of the k-th spontaneously induced radiation on the photodetector during the i-th count

S cki	1	2	3	4	5	6	7	8	9	10	11	12
S̅ c 1	2	3	4	5	6	7	8	9	10	11	12	13
S̅ c 2	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6	6,5
S̅ c 3	0,5	0,75	1	1,25	1,5	1,75	2	2,25	2,5	2,75	3	3,25
S̅ c 4	0,25	0,5	0,75	1	1,25	1,5	1,75	2	2,25	2,5	2,75	3

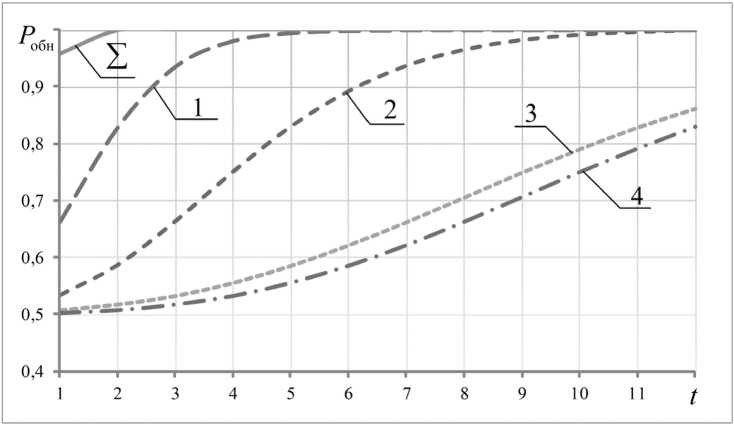
Рис. 4. Графики вероятности обнаружения в смеси сигнала спонтанно-индуцированного излучения суммарного и поканально

Fig. 4. Graphs of the probability of detection in a mixture of a signal of spontaneously induced emission of the total and channel-by-channel

С помощью исходных данных получим следующие результаты (рис. 4):

Заключение

При анализе полученных результатов можно сделать вывод, что при вероятности ложной тревоги ( F л.т. ), равной 10^–4, с вероятностью, близкой к единице, принятие решения о присутствии в принятой смеси сигнала спонтанно-индуцированного излучения ( P _обн) будет возможным на втором отсчете.

Полученные результаты показывают, принятие решения о присутствии в принятой смеси сигнала спонтанно-индуцированного излучения ( P обн ) поканально будет возможно с вероятностью, близкой к единице, в первом канале после 5 отсчета, во втором канале – после 10 отсчетов, а в третьем и четвертом каналах – после 12 отсчетов.

Полученные зависимости подтверждают возможность эффективно принимать решение о наличии или отсутствии в принятом сигнале спонтанно-индуцированного излучения. Решена задача обоснования рационального способа и алгоритма обнаружения совокупности спонтанных излучений, а также каждой составляющей в зависимости от дальности в типовых атмосферных условиях.