Методика обоснования электродинамических и конструктивных параметров поглощающих материалов волноводного типа

Цитирование: Ивенский, А.А. Методика обоснования электродинамических и конструктивных параметров поглощающих материалов волноводного типа / А.А. Ивенский // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(3). С. 272-283. DOI: 10.17516/1999-494X-0220

Проблемам создания материалов, предназначенных для ослабления коэффициента отражения при нормальном падении монохроматической электромагнитной волны на плоскую металлическую поверхность, посвящено большое количество работ [1-4].

С точки зрения радиофизики такие материалы характеризуются толщиной и отражательными характеристиками в заданном диапазоне длин волн. Здесь используется комплексный коэффициент отражения, определяемый как отношение амплитуд отраженной и падающей волн.

Задачей при разработке поглощающих материалов (ПМ) является обоснование их рациональных электродинамических и конструктивных параметров и получение минимального коэффициента отражения в максимально широком диапазоне длин волн.

Как известно, основными электродинамическими параметрами любого вещества, характеризующими взаимодействие электромагнитной волны с материалами, являются диэлектрическая ( ε = εʹ+εʺ ) и магнитная ( μ = μʹ+ μʺ ) проницаемости.

При этом параметры ε' и μ' связаны с передачей энергии ЭМИ, а ε'' и μ'' – с ее потерей или энергетическим рассеиванием в материалах за счет проводимости и резонансных механизмов.

Свойства поглощающих материалов могут быть улучшены за счет их магнитной проницаемости μ' . Однако известные магнитные материалы имеют значительный удельный вес и ограниченный рабочий диапазон температур, что снижает возможность их практического применения.

В связи с этим для расширения рабочего диапазона рассматриваются методы, где используются материалы с дисперсией диэлектрической проницаемости и структуры, в которых физическим механизмом поглощения электромагнитной волны является преобразование падающей плоской волны в поверхностную с последующим ее поглощением в толще материала.

Целью исследования выступает разработка методики обоснования электродинамических и конструктивных параметров поглощающих материалов волноводного типа.

Как известно, при разработке поглощающих структур приходится сталкиваться с разрешением следующего противоречия: стремление, с одной стороны, использовать материалы с максимально высокими значениями коэффициента поглощения, а с другой – обеспечить требования по согласованию электродинамических характеристик структуры материала с соответствующими характеристиками свободного пространства.

Для разрешения указанного противоречия в известной литературе [1] рассматривается подбор специальных сред и распределение их электродинамических и электрофизических характеристик по фазовому пространству материала. Обычно в поглотителе электромагнитных волн применяется градиентный рост проводимости в направлении задней стенки материала за счет увеличения концентрации и плотности поглотителя, который обеспечивает минимум отражения на передней кромке и максимум поглощения в толще.

Для создания поглощающих материалов с малым коэффициентом отражения ( R_отр <10 дБ) в широкой полосе частот в данной работе используется другой подход, основанный на выборе электродинамических и конструктивных параметров материала при решении задачи оптимизации в многомерном пространстве, где необходимо обеспечить максимальную широкополос-ность при заданном уровне отражательных характеристик материала.

Для разрешения указанной проблемы в качестве поглощающего материала в работе рассматривается конструкция, представляющая собой решетку – систему взаимно перпендикулярных полосковых элементов, изготовленных из диэлектрика и покрытых радиопоглощающим составом, которые располагаются на одинаковых расстояниях друг от друга (с постоянным шагом) (рис. 1).

Взаимная ориентация элементов решетки и всего ПМ относительно вектора поляризации падающего излучения дополнительно усложняет решение задачи оптимизации. Поэтому нами был избран путь поэтапного поиска экстремума с попеременной фиксацией ряда параметров и последовательного сужения диапазона изменения указанных переменных.

Многопараметрическую задачу оптимизации ПМ с точки зрения обеспечения минимума коэффициента отражения Rотр можно свести к исследованию его дифракционных свойств в зависимости от электродинамических характеристик при фиксированных геометрических параметрах решетки, обеспечивающих максимальное поглощение энергии электромагнитных – 274 –

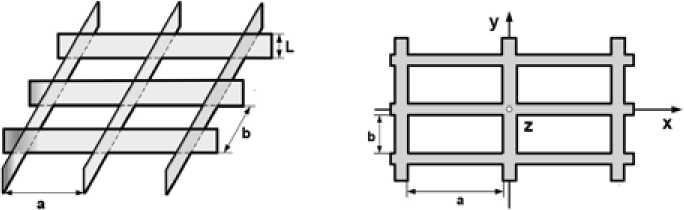
Рис. 1. Структура конструкционного поглощающего материала волноводного типа: L – ширина элемента (высота решетки); a, b – расстояние между элементами

Fig. 1. Structure of the structural absorbing material of waveguide type: L – element width (lattice height); a, b – distance between elements волн. Поиск экстремума осуществляли методом последовательных приближений [5], который позволяет достаточно быстро сформировать функционал от конструктивных и электродинамических параметров.

Исходными данными при решении задачи оптимизации параметров ПМ являются следующие:

по условиям наблюдения РЛС: длина волны падающего ЭМИ ( λ ), поляризация падающей волны;

по электродинамическим параметрам: проводимость элементов решетки ( σ ) и их толщина ( d ); проводимость ( σ _д), диэлектрическая ( ε) проницаемость среды, заполняющей решетку;

по конструктивным параметрам: геометрические размеры ячейки ПМ (длина – а , ширина – b , высота – L, d – толщина).

При описании взаимодействия ЭМИ с ПМ за основу взят механизм распространения монохроматического электромагнитного поля в прямоугольной ячейке ПМ как по прямоугольным волноводам с импедансными стенками, заполненными диэлектриком. При этом источник ЭМИ находится за пределами рассматриваемой части линии передачи и создаваемая им волна распространяется вдоль оси Z (рис. 2).

Определим значения критической длины волны, зависящей от типа волны, формы и размера поперечного сечения ячейки волноводного типа по формуле [6]

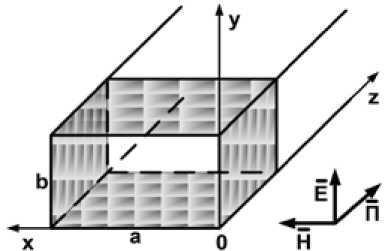
Рис. 2. Схема взаимодействия ЭМИ с ячейкой поглощающей решетки с поперечным сечением а и b

Fig. 2. The scheme of interaction of EMI with a cell of the absorbing lattice with cross section a and b

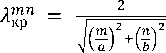
Как известно, низшей волной, для которой λ_кр имеет наибольшую величину, в прямоугольной ячейке при a>b явля етс _^ я волна тип а Н 10. Это осно вно й тип волны в прямоугольной ячейке, так как он обеспечивает одномодовый (одноволновый) режим работы. При условии (l)

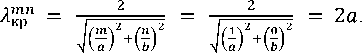
При распространен ии электромагнитного поля в толще ПМ учитывали, что амплитуда

.

вектора напряженности эле ктрическог о п оля Е умен ьш ается по экспоненциальному закону и характеризуется коэффициен том затухания (вдоль оси OZ ):

E(z) = Eo ∙e hz.

Тогда выражение для м ощ ности, переносимой через поперечное сечение ячейки, будет иметь вид

( ) ) = P_o ∙    21 .

В связи с тем, что погл ощение (зат _^ уха ние) электр ома _^ гнитных волн в линиях передачи обусловлено потерями мощ н ос т и, к ^ оторые возникают вследствие конечной проводимости элементов решетки (σ ≠ ∞) h'', и потерями в диэлектрике hд'', заполняющем ячейку (σд ≠ 0), показатель затухания волны в яче й к ^{^} е П М

h4H10) = ;     1-(2J ] ⁄ ∙ 1 + "      । ,                     (5)

где R_s – поверхностное сопротивление полоскового элемента ячейки определяем с использованием выражения

--

^s = У **w /2 , где μ = 4π·107 – магнит ная по сто^янная; ω = 2πf – круговая частота; f – рабочая частота; σ – проводимость элементов р еш е т к и; ZH10 – характеристическое сопротивление ячейки ПМ, которое вычисляем по формуле zc

2н'10 ""             ^                                                                            (7)

(2 J где Zc – сопротивление сре^ ды, заполняющей ячейку, которое находим из выражения

120л:/ 1 Д д

!д, д где εд, μд – диэлектриче ск^ ая и магнитная проницаемости среды в ячейке соответственно.

Как известно, поте ри в диэлектрическом заполнении описывают с помощью выражения [6]:

ℎд

Л £_д ta n 5

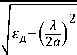
где тангенс угла диэлектр иче ских потерь определяем с помощью выражения

ta = д , ^д где ε0 = 10–9/36π – диэл ект рическая постоянная; σд – проводимость среды; εд – диэлектрическая проницаемость наполн ите ля в ячейках.

Таким образом, сум мар ная постоянная затухания волны в ячейке с учетом выражений (5) и (9) имеет вид

ℎ^

1- пт^{1 ⁄2} ∙ 1+ -Hl + ⁷¹: ^д    .

z , lie ■H                     L a \2a) J л I ‘ д \2a/

Для описания отражательных характеристик ПМ на основе поглощающих решеток в работе принято следу ющ ее допущение: вся мощность падающей электромагнитной волны распределяется на две составляющие, одна из которых отражается сразу от поверхности ПМ, а другая проходит внутрь решетки, поглощается в толще ПМ, отражается от металлического объекта (подложки) и так же выходит наружу. Затем эти составляющие с учетом фазы суммируются.

,

Для определения коэффициентов отражения от решетки ПМ К₁ и прохождения электромагнитных волн в его тол щу К2 воспользуемся выражениями, описывающими отражательные характеристики идеально проводящих периодических структур [8]:

—-) Inch.—

-l+l^-J ln\sh— J   Inch——i-ln2lsh-Q-\

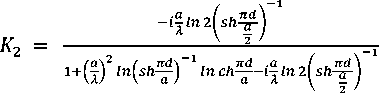
Для описания поглощения ЭМИ на элементах решетки в работе предложено учесть ослабление мощности в толще ПМ (4). С учетом выражений (4), (11) – (13) суммарный коэффициент отражения по мощ ности R_отр для элементов решетки с импедансным покрытием имеет вид

—Inlsh— I Inch—

. Г<Л² , ( , 7Td\^-1 ,     , nd .a ,            \

—H-f^-1 Inlsh— I Inch— —i^-Zn2lsh—1

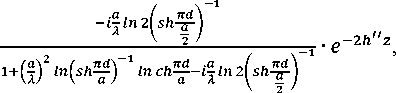
где z принимаем за ширину (высоту) решетки L .

Таким образом, на основе приведенных выражений и с учетом требований к параметрам ПМ, обеспечивающим заданный коэффициент отражения Rотр <10дБ, разработан алгоритм определения электродинамических и конструктивных параметров ПМ, представленный на рис. 3.

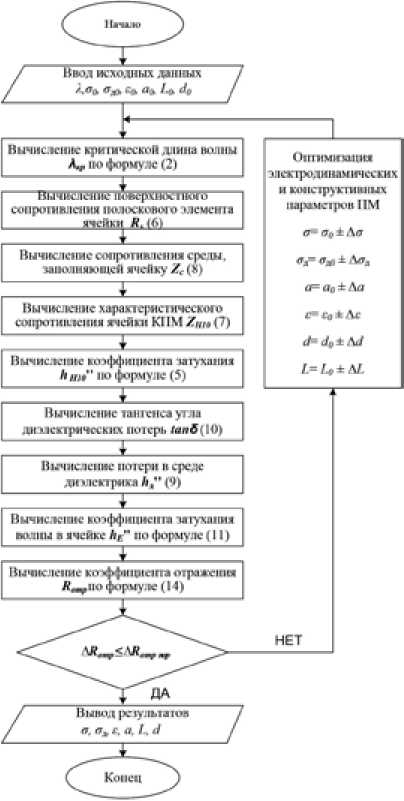
Рис. 3. Алгоритм определения электродинамических и конструктивных параметров поглощающего материала

Fig. 3. Algorithm of determination of electrodynamic and design data of the absorbing material

Алгоритм определения параметров ПМ заключается в следующем:

• 1.    Задаем исходные данные: длина волны λ ; проводимость элемента решетки σ ₀; проводимость среды σ д0; диэлектрическая проницаемость среды ε 0, заполняющей решетку; геометрические размеры ячейки: а ₀ – широкая сторона, L ₀ – высота, d ₀ – толщина.

• 2.    Находим значения критической длины волны λкр по формуле (2) для заданных размеров прямоугольной ячейки ПМ.

• 3.    Рассчитываем значения постоянной затухания волны hН10 '' в ячейке (5), для этого находим значения поверхностного сопротивления полоскового элемента ячейки R_s (6), характеристического сопротивления ячейки ZH10 (7) и среды Zc (8), заполняющей ячейку.

• 4.    Определяем потери диэлектрического заполнения ячейки h _д'' по формуле (9), для этого рассчитываем тангенс угла диэлектрических потерь tanδ по формуле (10).

• 5.    С помощью выражения (11) вычисляем значения суммарного показателя затухания в ячейке h Σ.

• 6.    На основе выражения (14) находим коэффициент отражения R_отр .

Если полученное значение коэффициента отражения ЭМИ по мощности не удовлетворяет критерию ∆R_отр ≤ ∆R_{отр пор} , то осуществляется варьирование параметров ПМ с шагом ∆ : проводимость элемента решетки ∆σ ; проводимость среды ∆σ д; диэлектрическая проницаемость ∆ε среды, заполняющей решетку; геометрические размеры ячейки: ∆а – широкая сторона, ∆L – высота, ∆d – толщина. Рассчитанные параметры, при которых ∆Rотр ≤ ∆Rотр пор , принимают для разработки ПМ, удовлетворяющих данному условию.

На основе представленного алгоритма была разработана программа и получены частотные зависимости суммарной постоянной затухания h _Σ'' и суммарного коэффициента отражения Rотр от параметров предложенного выше ПМ: проводимости материала ячейки, диэлектрической проницаемости и проводимости среды, геометрических параметров ячейки (длины, высоты и толщины).

На рис. 4, 5 приведены результаты исследований коэффициента затухания h _Σ'' и коэффициента отражения по мощности Rотр для различных поперечных сечений ячейки волноводного типа в диапазоне длин волн λ = 1…10 см.

Как было отмечено ранее, условием распространения в ячейке ПМ основного типа волны Н ₁₀ является а<λ<2а. Анализ приведенных зависимостей показал, что при значениях λ, близких к λ ¹⁰ кр = 2а , ПМ может пропускать очень малую мощность, что приводит к росту коэффициента затухания основной волны. Если λ приближается к λ²⁰ _кр = а, уменьшается затухание высших типов волн, возникающих на нерегулярностях в реальном тракте.

Результаты исследования влияния удельной проводимости элементов ячейки на коэффициент отражения R _отр в диапазоне длин волн λ = 1…10 см изображены на рис. 6.

Из приведенных зависимостей следует, что при значении σ = 0,4 см/м коэффициент отражения R _отр не превышает порогового значения.

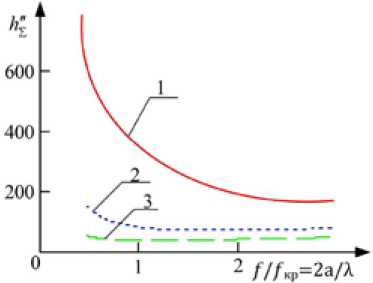
Рис. 4. Частотная зависимость коэффициента суммарного затухания h _Σ'' при σ = 0,4 см/м для различных значений стороны ячейки а: 1 – 1,3 см; 2 – 2,3 см; 3 – 3,5 см

Fig. 4. Frequency dependence of coefficient of total attenuation of h Σ ’’ at σ = 0.4 cm/m for various values of the party of a cell a : 1 – 1.3 cm; 2 – 2.3 cm; 3 – 3.5 cm

Исследования влияния потерь в диэлектрике на коэффициент отражения ПМ R _отр в диапазоне длин волн λ = 1…10 см (рис. 7) показали, что проводимость среды σд существенно влияет на уровень отраженного излучения. Так, при значении σ_д = 10^-15…10^-2 коэффициент отражения R отр не превышает порогового значения.

Исследования влияния на коэффициент отражения R_отр различных относительных диэлектрических проницаемостей среды ε в диапазоне длин волн λ = 1…10 см отражены на рис. 8.

Анализ этих зависимостей показал, что с уменьшением относительной диэлектрической проницаемости наполнителя в ячейках ПМ изменяется частотный диапазон коэффициента отражения R отр. Установлено, что наибольшей широкополосностью обладает ПМ с диэлектрическим заполнением ε = 2, что соответствует материалам типа полиэтилен, полистирол, пенополиуретан и т.п.

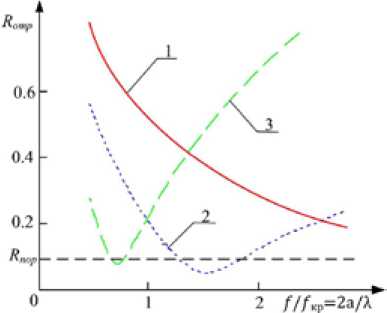
Рис. 5. Частотная зависимость коэффициента отражения по мощности R _отр при σ = 0,4 см/м для различных значений стороны ячейки а: 1 – 1,3 см; 2 – 2,3 см; 3 – 3,5 см

Fig. 5. Frequency dependence of coefficient of reflection on R reflec power at σ = 0.4 cm/m for various values of the party of a cell a : 1 – 1.3 cm; 2 – 2.3 cm; 3 – 3.5 cm

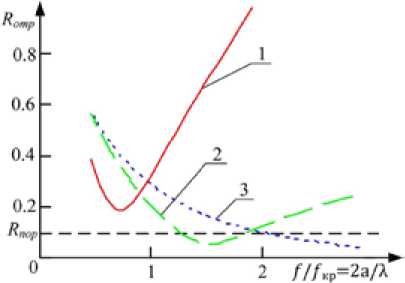
Рис. 6. Частотная зависимость коэффициента отражения по мощности R _отр для разной удельной проводимости элементов ячейки σ: 1 – 10⁷ см/м; 2 – 0,4 см/м; 3 – 0,1 см/м

Fig. 6. Frequency dependence of coefficient of reflection on R reflec power for different specific conductivity of elements of a cell σ: 1 – 10⁷ cm/m; 2 – 0.4 cm/m; 3 – 0.1 cm/m

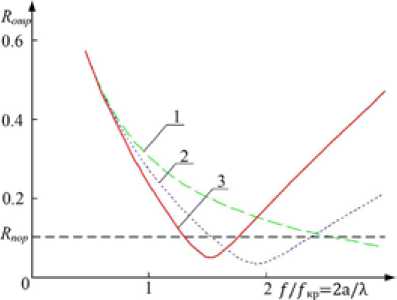
Рис. 7. Частотная зависимость коэффициента отражения по мощности R _отр при σ = 0,4 см/м для различной проводимость среды о_д: 1 - 1 см/м; 2 - 10^-2 см/м; 3 - 10^-15 см/м

Fig. 7. Frequency dependence of coefficient of reflection on R reflec power at σ = 0.4 cm/m for various conductivity of the environment о d : 1 - 1 cm/m; 2 - 10^-2 cm/m; 3 - 10^-15 cm/m

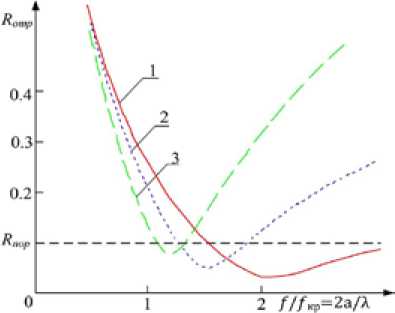
Рис. 8. Частотная зависимость коэффициента отражения по мощности R _отр при σ = 0,4 см/м для различных относительных диэлектрических проницаемостей среды ε: 1 – 1; 2 – 2; 3 – 6

Fig. 8. Frequency dependence of coefficient of reflection on R reflec power at σ = 0.4 cm/m for various relative dielectric pronitsayemost of the environment ε: 1 – 1; 2 – 2; 3 – 6

Результаты исследования влияния различной высоты радиопоглощающей решетки (глубины ячейки) ПМ на коэффициент отражения R _отр приведены на рис. 9.

Из приведенных зависимостей следует, что при значении L = 1 см коэффициент отражения R _отр в широком диапазоне длин волн не превышает порогового значения.

Результаты исследования влияния на коэффициент отражения R отр различной толщины поглощающего покрытия на элементах решетки ( d = 1х10^-3; 1х10^-2; 1х10^-1 см) в диапазоне длин волн λ = 1…10 см можно видеть на рис. 10.

Из приведенных зависимостей следует, что значение порогового коэффициента отражения R _отр достигается при d <10^-2 см.

Таким образом, на основе разработанной методики, заданных условий наблюдения и характеристик зондирующего ЭМИ может быть обоснован выбор электродинамических – 281 –

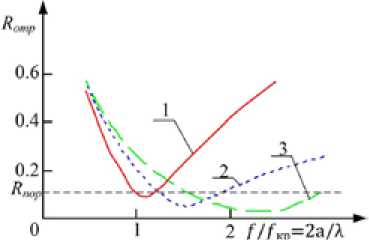
Рис. 9. Частотная зависимость коэффициента отражения по мощности R _отр при σ = 0,4 см/м, σ_д = 10^-15 см/м, ε = 2 для различной высоты элементов ячейки поглощающего материала L : 1 – 0,5 см; 2 – 1 см; 3 – 1,5 см

Fig. 9. Frequency dependence of coefficient of reflection on R reflec power at σ = 0.4 cm/m, σ д = 10^-15 cm/m, ε = 2 for various height of elements of a cell of the absorbing material L: 1 – 0.5 cm; 2 – 1 cm; 3 – 1.5 cm

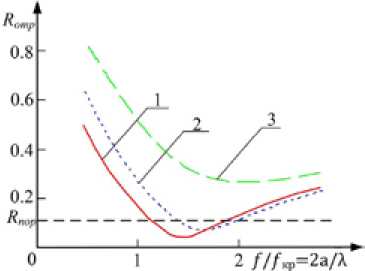
Рис. 10. Частотная зависимость коэффициента отражения по мощности R отр при σ = 0,4 см/м, σ д = 10^-15 см/м, ε = 2, L = 1 см для различной толщины поглощающего покрытия на элементах решетки d : 1 – 10^-3 см; 2 – 10^-2 см; 3 – 10^-1 см

Fig. 10. Frequency dependence of coefficient of reflection on Rreflec power at σ = 0.4 cm/m, σd = 10-15 см/м, ε = 2, L = 1 cm for various thickness of the absorbing covering on lattice elements d: 1 – 10-3 cm; 2 – 10-2 cm; 3 – 10-1 cm и конструктивных параметров поглощающих материалов волноводного типа: поперечного сечения ячейки, проводимости и толщины покрытия радиопоглощающей решетки, диэлектрической проницаемости среды, заполняющей решетку, толщины поглощающего материала.