Методика обработки профилограмм с использованием вейвлет-фрактального анализа

В настоящей статье исследуется подход к установлению корреляции «эволюция динамической системы - эволюция качества трущихся поверхностей». Установление данных зависимостей является базой автоматизации контроля качества поверхностей в процессах трения. На кафедре мехатроники СПбГУИТМО с помощью системы «ТРИБАЛ-2» были проведены опыты по трению. Внутренняя динамика трения была исследована в результате обработки с помощью вейв-лет-анализа, а также расчетами фрактальных размерностей с помощью программы Fractan полученных профилограмм трибопар. Исследование внешней динамики совершено по методике, описанной в [1]. В результате работы на ТРИБАЛе были получены входные и выходные данные процесса трения, которые в последующем были обработаны с помощью пакета System Identification Toolbox системы Matlab. В итоге представлены полученные результаты.

Анализ шероховатости поверхности

Микрогеометрия поверхности представляет собой геометрический объект, относящийся к классу фракталов. В основе оценок шероховатости лежат подходы к вычислению стохастических характеристик фрактальных геометрических объектов, которые интерпретируются как сигналы в нелинейных системах [1].

Показатель Херста

Исследование временного ряда, в роли которого выступает шероховатость, осуществляется с помощью метода нормированного размаха. Данный метод применяется при исследовании последовательности измерений температуры атмосферного воздуха, количества осадков, параметров стока рек и т.п. [3].

Нормированный размах определяется следующим образом. Пусть x(t) - некоторая случайная величина, рассматриваемая в некоторые дискретные промежутки времени ti в течение периода наблюдений г, 1 т xx (г )) = ^ x (ti) - ее среднее значение, а г i=1

J Г

- i[ x(ti)-(x(г м                    (1)

^г i = 1

стандартное отклонение x .

t

X (t, г ) = Z[ x (u)-(x (г ))]•                      (2)

u = 1

Приведенное выражение является накопившимся отклонением значений случайной величины x ( t ) от ее среднего значения < x> за время t . Разность между минимальным и максимальным значениями X ( t ,т) называется размахом R (т).

R ( т ) = max X ( t , т ) - min X ( t , т ) ,

где 1< t <т. Рассматриваемый размах R (т) явно зависит от периода т и растет вместе с ним. Безразмерное отношение R / S позволяет сравнивать размах для разных явлений. Было выявлено, что нормированный размах R / S хорошо описывается эмпирическим соотношением

R

S

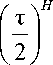
Данное соотношение получило название закона Херста, а показатель H - коэффициент Херста.

Вейвлет-преобразование

Для дискретного сигнала конечной длины N вейвлет-преобразование вычисляется для дискретных значений параметров масштаба a = 2 j и сдвига d = к 2 j , где k , j - целые числа. Вейвлет- и масштабирующие функции имеют вид

V j,к (t ' 27 ^ 2 - k) , Ф j, к ( t ' 17 ^ 2 - к) .

Дискретное преобразование сигнала на j -м уровне разложения можно выразить следующим образом:

^k max

Wj-Е а, к фл к (t )+Е dj, к vj, к (t).

к-0

Вейвлет-коэффициенты j и j задаются интегралами aj,к = Jx(t)ф*-,к (t)dt, dj,к = jx(t)v*,к (t)dt.

На последнем уровне разложения m формируются наборы коэффициентов аппроксимации последнего уровня и детализирующих коэффициентов всех уровней. Для восстановления сигналов по известному набору коэффициентов используется каскадный алгоритм обратно- го вейвлет-преобразования. Анализируемый сигнал равен сумме сглаженного компонента последнего уровня (Am) и деталей всех уровней разложения (Dm,...,D1):

k max                       m k max

x (ti ) = Am (ti ) + Dm (ti ) + -D1 (ti ) = E am,kФm,k (t) + EE dj,kV J,k (t)• (8)

k - 0                       J - I k - 0

Параметры действия спектральной плотности энергии

Спектральная плотность энергии равна квадрату фурье-преобразования сигнала:

E ( f )-| X ( f )’-Ux (') e ^ i"»t ’•

где X ( f ) - спектр сигнала.

Частотное накопление спектральной плотности энергии (кумуля- ^f 2

та) в пределах полосы частот ( f , f , ) определяется как 8 - J E ( f ) d f .

f i

Размерность кумуляты определяется в Дж/с = Вт.

В качестве характеристик спектральной плотности энергии используются номинальный и интервальный параметры действия:

*

hi =

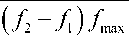
, h 2

^E max

f max

где E _max - максимальное значение спектральной плотности энергии, f ax - максимальная частота, соответствующая E _max, С - предельное значение спектральной плотности энергии. Наиболее целесообразно использование параметра h i .

Автокорреляционная и взаимная корреляционная функция

По записям входного u ( t ) и выходного сигналов y ( t ), полученных при испытаниях образцов, оценивается автокорреляционная и взаимная корреляционная функции. Автокорреляционная функция случайного процесса характеризует общую зависимость значений процесса в некоторый данный момент времени от значений в другой момент. Взаимная корреляционная функция двух сигналов характеризует общую зависимость значений одного сигнала y ( t ) от значений другого u ( t ) [1].

Исследования

Исследование процесса трения проводилось на трибометрической установке «ТРИБАЛ» [2]. Возвратно-поступательное движение исследуемых образцов осуществлялось с постоянной скоростью, при фиксированной величине нормального нагружения, в режиме сдвига фаз кривых перемещения (в данном режиме осуществляется движение с трением скольжения). В качестве исследуемого материала был использован сплав Л56, предварительно обработанный по 9-му классу точности - шероховатость исследуемой поверхности Ra составила 0,22 мкм. Для проведения испытаний были изготовлены образцы для трехточечного контакта.

Опыты трения проводились следующим образом: сначала устанавливался первый набор исследуемых образцов, в течение определенного времени длилось испытание, после проведения опыта первый набор снимался для дальнейших исследований шероховатости после трения, а в ТРИБАЛ устанавливался следующий набор пар трения для проведения испытания при иной длительности опыта. Всего было проведено 5 испытаний на трение с различными временными промежутками: 30, 40, 60, 90, 120 мин. В каждом испытании системой «ТРИБАЛ» также фиксировались входные u ( t ) и выходные y ( t ) данные для последующей идентификации процесса трения.

После опытов трения было проведено исследование шероховатости поверхности. С помощью профилографа записывался профиль поверхностей трения для каждого образца. Снятие профилограмм для каждого из них осуществлялось в трех направлениях: вдоль, поперек и под углом 45° относительно возвратно-поступательного движения, совершаемого образцами.

Обработка полученных данных

При обработке полученных шероховатостей были применены методы вейвлет-фрактального анализа с использованием пакета Matlab. Профилограмма представляет собой дискретный ряд {x(ti )}^1, мкм, значений пиков и впадин рельефа поверхности трибопары. Для обработки использовался многоуровневый вейвлет-анализ [4]. Сначала было произведено разложение сигнала профилограмм до уровня N = 3, в результате чего получены детализирующие коэффициенты. Далее, для нахождения частотных компонент сигнала проведено восстановление отдельно по каждому набору детализирующих коэффициентов. Для каждого компонента сигнала был проведен спектральный анализ и по- лучены графики спектральной плотности энергии и накопления энергии - кумулята (рис. 1).

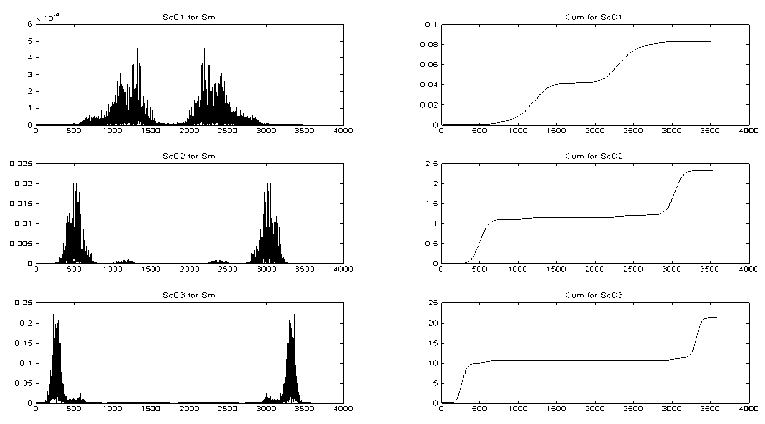
Рис. 1. Энергетические спектры и кумуляты образца.

Стохастические характеристики. Частотные компоненты сигнала профилограмм имеют фрактальную размерность. Для оценки хаотичности компонент (вейвлет-коэффициентов) использовался показатель Херста. Показатель Херста H описывает вероятность того, что два соседних отчета могут быть одинаковыми. Имеет место формула H = 2 -D F , где D F - фрактальная размерность, которая определяется как предел [4]:

D = lim ln M ^(Е) (11)

DF lim«0ln (1/ 8) . (ll)

Для вычисления коэффициента Херста использовалась программа Fractan.

В результате анализа данных были получены графики эволюции параметров шероховатости Ra, предельных значений кумулят и коэффициентов Херста частотных компонент сигналов профилограмм.

На рис. 2, 3, 4, 5 соответственно представлены графики эволюций для направлений вдоль (верхние и нижние образцы) и поперек. Заметен колебательный характер изменения шероховатости, что может быть объяснено приработкой поверхностей. Наблюдается колебательный характер изменения показателя Херста на всех частотах сигнала. Также видно, что эволюция шероховатости коррелирует с параметрами действия на высоких частотах.

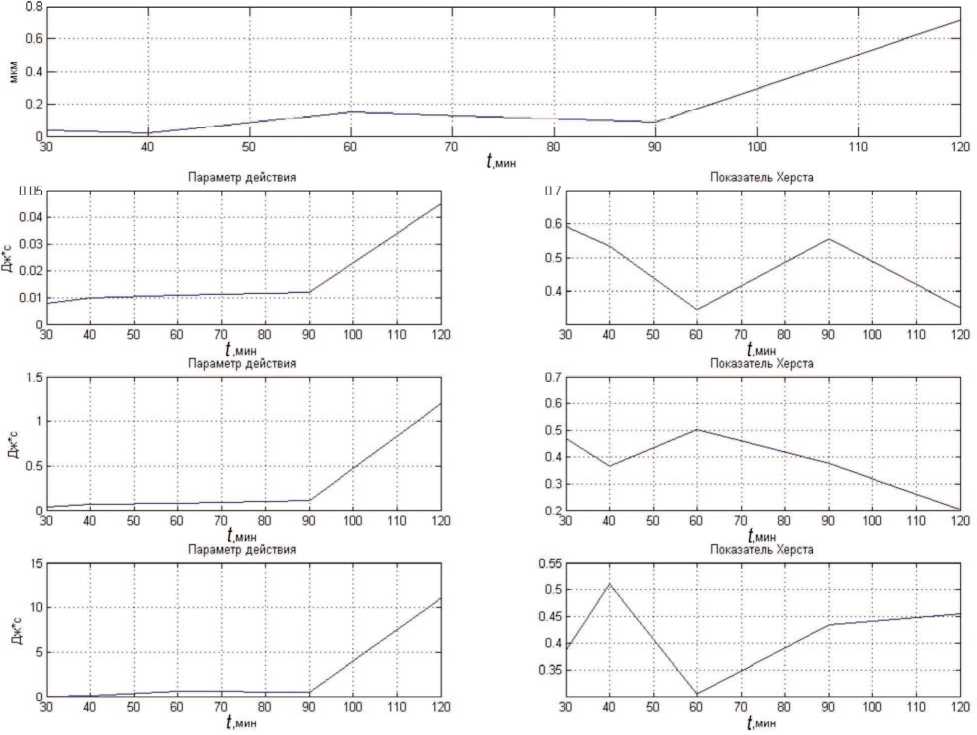
Рис. 2. Эволюция шероховатости верхних образцов (вдоль)

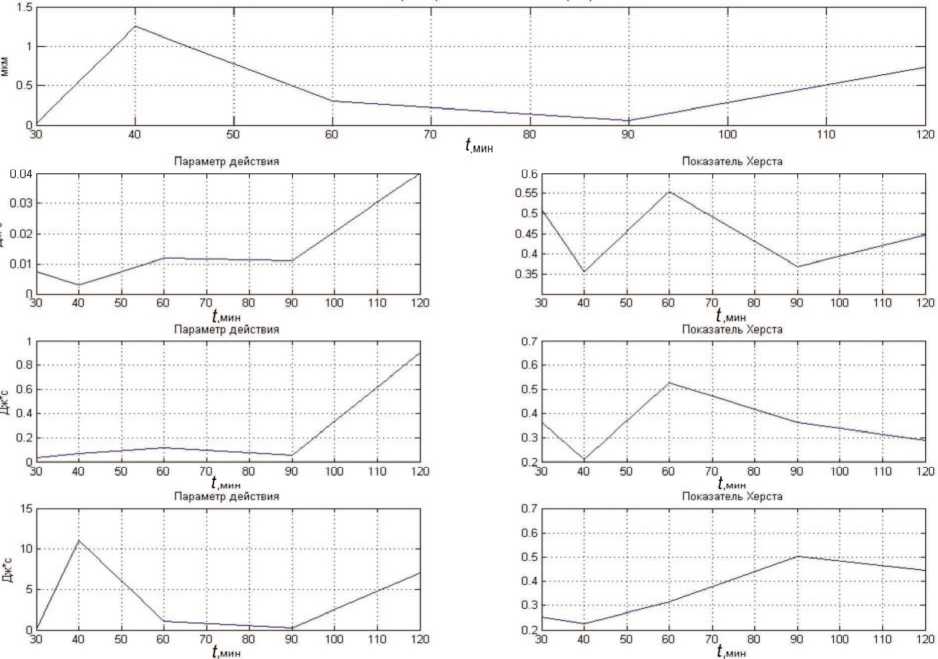
Рис. 3. Эволюция шероховатости нижних образцов (вдоль)

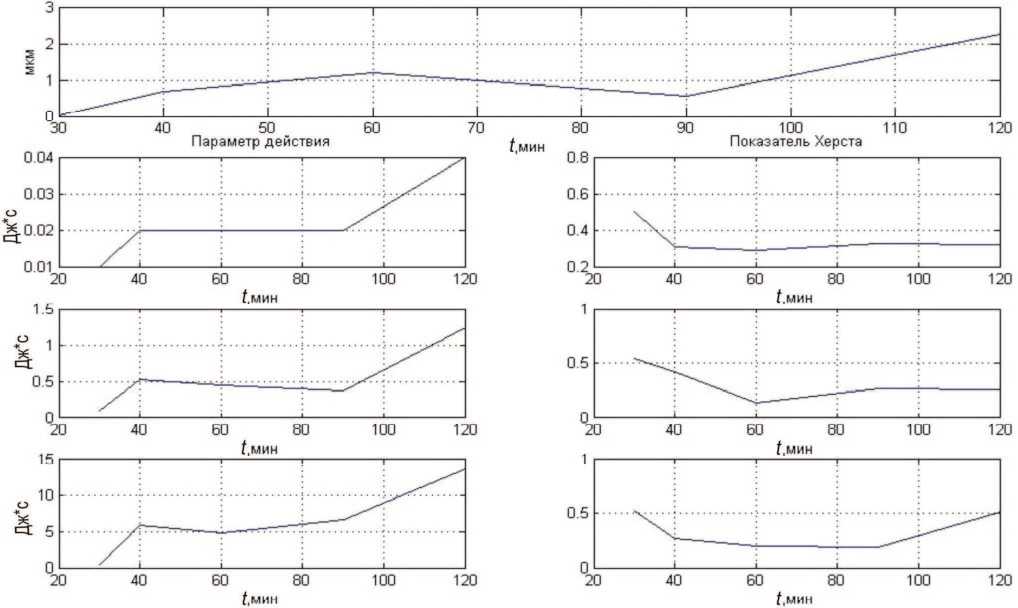
Рис. 4. Эволюция шероховатости верхних образцов (поперек)

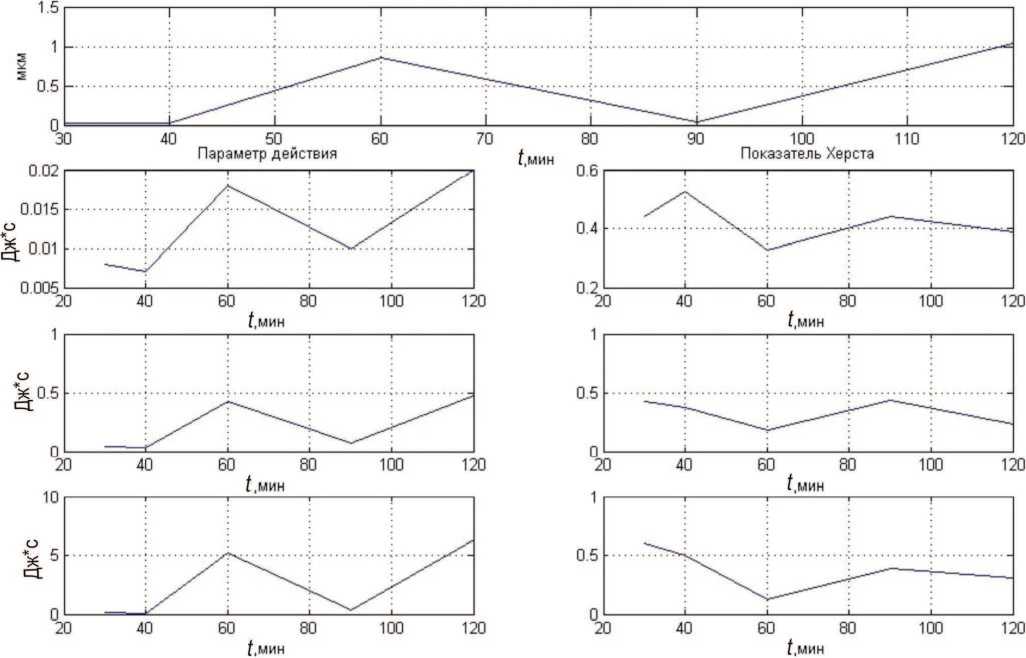
Рис. 5. Эволюция шероховатости нижних образцов (поперек)

Заключение

В результате анализа данных были получены графики, характеризующие внутреннюю динамику процесса: эволюция параметров шероховатости Ra, предельные значения кумулят и коэффициенты Херста частотных компонентов сигналов профилограмм. Было установлено, что показатель Херста имеет колебательный характер, который указывает, на колебательность устойчивости и неустойчивости состояния поверхностного слоя взаимодействующих контрпар.