Методика оценки допустимых значений параметров аэродинамической и инерционной асимметрии марсианского зонда

Задача проектирования космического аппарата (КА), осуществляющего спуск в марсианской атмосфере, начинается с выбора его внешней формы, в качестве которой часто выбирается сегментальноконическая форма [1-5]. В частности, в работах [6; 7] содержится обсуждение выбора формы КА, спроектированного для спуска в марсианской атмосфере. Следующим этапом проектирования является выбор проектных параметров спускаемого космического аппарата. Отметим, что алгоритм установления допустимых величин переменных как малой аэродинамической, так и малой массовой асимметрии рассматривались в [8-10]. Дополнительно, алгоритм установления допустимых величин переменных малой инерционной и массовой асимметрии КА обсужден в [11-13]. В этой статье рассматривается алгоритм определения допустимых величин переменных малой аэродинамической и инерционной асимметрии КА без смещения центра масс космического зонда (без массовой асимметрии), осуществляющего

неуправляемый спуск в марсианской атмосфере. Практическая ценность полученных допустимых величин переменных асимметрии КА заключается в том, что разнообразные комбинации асимметрий могут стимулировать реализации эффектов длительного или вторичного резонанса, которые увеличивают значения угловой скорости или значения пространственного угла атаки [10; 11; 14] и могут приводить к аварийным ситуациям, связанными со сбоями в функциональности тормозной парашютной системы. Таким образом, определения допустимых величин переменных малой аэродинамической и инерционной асимметрии КА при спуске в нестабильной разряженной атмосфере Марса является актуальной задачей современной космонавтики, так как существующие задачи по этой теме не рассматривают компенсацию аэродинамической и инерционной асимметрий.

Методология проектирования

В данной работе рассматривается методология проектирования космического зонда, совершающего вращение с малой угловой скоростью, образованной при отделении данного космического зонда от базового космического аппарата.

Постановка задачи проектирования предполагает определение максимальных величин переменных инерционной и аэродинамической асимметрии, с которыми не повышается угловая скорость ω _x к максимальным значениям, приводящих к главному резонансу:

max(ω x ) ≥ ω x ≥ min(ω x ).           (1)

С этой целью на обобщенный параметр асимметрии накладываем ограничение:

|q| = | m J<|Q „ I,               (2)

где mA = mA ®-2; mA = V(mA )2 + (mA )2;

A       Ю       f            2         A       to       f           2

mt =-- m y 0 ^- I xz to x ;   m 2 =-- m o + I xy ^to x ;

^mz 1                          ^mz 1

Ω _p – максимальное значение параметра Ω; m^f_yti , mf — безразмерные параметры, характери

зующие аэродинамическую асимметрию космического аппарата; I^ , I ^ - безразмерные параметры, характеризующие инерционную асимметрию кос-

мического аппарата.

В этих выражениях явно отсутствуют параметры, характеризующ ие ма ссовую асимметрию космического аппарата A y , Az , так как не учитывается смещение центра масс КА.

Далее условие (2) представляется в следую-

щем виде:

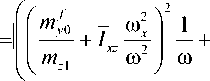
Том 7

Система уравнений (4) имеет следующее тривиальное решение:

m _y ^f ₀ = m _z ^f ₀ = 0,      I _xz = I _xy = 0.

Следовательно, система уравнений (4) не имеет стационарных точек кроме значений mf= m f = 0, I = I = 0. По этой причине эти y 0z0        xz     xy параметры асимметрии достигают своих наибольших границ только на границе рассматриваемой области. В неравенстве (3) имеется 4 неизвестных, следовательно, у него бесконечное множество решений. Однозначное определение допустимых областей mf 0, mf, I xz, I возможно при задании весовых соотношений между этими величинами. Запишем параметры асимметрии в виде весового соотношения [8; 9]:

mf = mr U, mZ0 = mF U, PP

Ixy = (1—Ix) и, Ixz = (1—Ix) и; xyxz

P3

U = pm^ = p2 m0 =

mz 1

=p'x 3(1 - Ix )

m z 1

I xz

= 4(1 - 4 Г

В

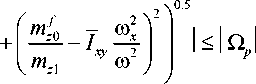
случае главного резонанса получаем:

где P i - положительные веса, для которых равен-

ство ^ P_t = 4 справедливо.

i = 1

ωxр =ω 1-Ix.

Значения веса P i в уравнении (6) определяются, чтобы при достижении максимальных величин угловой скорости Q неравенство (3) выполнялось. С целью становления диапазона безразмерных переменных асимметрии перепишем условие (3) с учетом формул (5) и (6) в виде:

Для определения максимального значения обобщенного параметра асимметрии Ω запишем необходимое условие существования экстремума и определим значения безразмерных параметров, характеризующих аэродинамическую и инерционную асимметрии космического зонда:

In p |>	( U 2 "P2 + V P 1	U 2 U 2 22 P 2    P 3	+
U 2	U 2	U 2	0.5
+-- у + 2---- 2 4      23		+ 2--- PP P 1 P 4 >

Условие (7) можно переписать в более ком-

5Q	1	m ±+ .x^ у m A 1    1 - I x	^	= 0
5 m f	m z 1^
5Q	1	f mf 7 m z 0       xy	3	= 0,
5 m A o	m z Р	у mz 1    1 - Ix	J

пактном виде:

Iq I > и Сс,

где C =

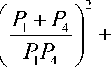
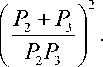
5Q	1		Г I xz	f >  + m^ mz 1 V	= 0,	(4)
d I xz	Q(1-	I x )	У 1 - I x
5Q	1		Г I xy_	f m z 0	= 0.
d I xy	Q(1-	I x )	У 1 - I x	m z 1 J

Учитывая неравенство (3) и решая его с учетом неравенства (7), найдем искомую область допустимых значений в следующем виде:

Ω U≤ p.

C

С учетом формулы (5) получаем диапазон безразмерных переменных асимметрий m f₀, m ^f₀, ¹ xz , ¹ xy *

^f y 0

<

^f z 0

xy

<

xz

<

a p

a p

» p

5 p

C

² m_{z 1}

2 -

² m_{z 1}

(1 - I x )

,

2 (1 - I X )

P 4

.

При этом, если данные переменные асимметрий оправдывают уравнение (3), то максимальное значение угловой скорости, при которых реализуется главный резонанс, не достигается. На рис. 1 представлен алгоритм установления допустимых значений переменных малой массовой асимметрии, как и малой инерционной асимметрии.

Численное решение задачи определения допустимых значений параметров асимметрий начинается с ввода исходных начальных, геометрических и инерционных данных космического зонда.

Далее задаются величины весов P_i с сохра- ⁴

нением равенства (6) и условия ^ P_t = 4. Далее производится расчет обобщенно го параметра асимметрии Ω _p с помощью неравенства (7). В дальнейшем рассчитывается область параметров асимметрий с помощью неравенств (9), проверяется выполнение условия Ω ≤ Ω _p с помощью уравнения (2). После выполнения верификационных расчетов по нелинейным исходным уравнениям сохраняются полученные области, и программа завершает работу.

Реализация алгоритма 1 с предрассчитан-ными выражениями на космическом зонде с аэродинамической и инерционной асимметрией даст интервал значений параметров асимметрии, обеспечивающих спуск в атмосфере без возможности появления длительного или вторичного резонанса.

Рассмотрим применение предлагаемой методики определения допустимых величин переменных асимметрий на примере КА Mars Polar Lander [5], спускающегося в марсианской атмосфере (рис. 2). КА Mars Polar Lander имеет следующие массово инерционные характеристики: высота конуса аппарата l = 2 м, радиус основания конуса аппарата r = 1,25 м, масса космического аппарата m = 576 кг, момент инерции аппарата I_x = 270 кг∙м², I_y = I_z = 443 кг∙м². Принимаются

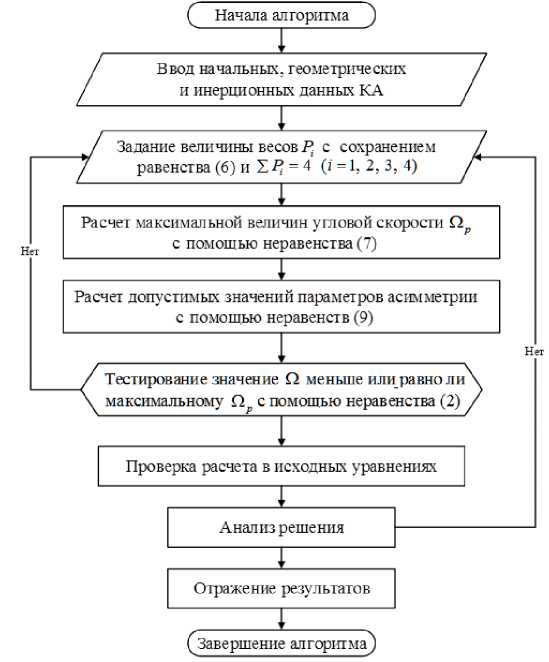
Рис. 1. Алгоритм установления допустимых значений переменных малой массовой асимметрии, как и малой инерционной асимметрии

Том 7

Рис. 2. Спускаемый марсианской космический аппарат Mars Polar Lander [5]

V (0) = 3400 м/с, угол наклона траектории аппарата 0(0) = 0,017 рад. Веса P i из уравнения (6) были заданы следующими значениями: P j = 1,5, P 2 = 1,5, P ₃ = 0,5, P ₄ = 0,5. Для приведенных начальных данных со значением Ω _r = 0,47 искомый диапазон допустимых величин инерционной асимметрии и аэродинамической асимметрии рассматриваемого космического аппарата носят следующие значения:

m^, mf е [0; 0,0133];

Ц , I_xz е [0; 0,078].

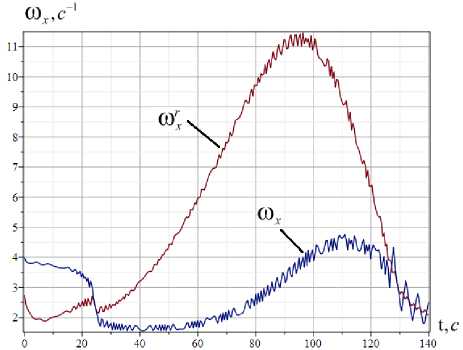
Численное решение системы уравнений (1) в [15] на примере КА Mars Polar Lander (рис. 3)

показывает, что при максимальных значениях интервала (10) не появился главный резонанс, а при повышении этих величин в 1,2 раза появился главный резонанс в близости максимума резонансного значения угловой скорости, соответствующего максимуму скоростного напора.

следующие первоначальные условия спуска космического аппарата: первоначальная высота полета H (0) = 110 км, начальная скорость полета

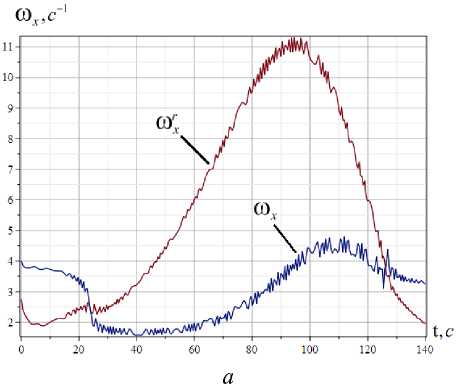
Рис. 3. Угловая скорость ω _x и резонансные значения угловой скорости ω ^r при атмосферном спуске косм и чес к ого зонда: а – при m _y ^f ₀ , m _z ^f ₀ = 0,0133; I _xy , I _xz = 0,078;

б

б – при myf0, mzf0=0,0160; Ixy, Ixz = 0,094

Заключение

В этой работе рассмотрена методика оценки допустимых величин переменных малой аэродинамической асимметрии, как и малой инерционной асимметрии космического зонда, совершающего неуправляемый спуск в разреженной атмосфере Марса. Использование полученной оценки при проектировании космических зондов позволяет исключить нерасчетное влияние резонанса на из- менение величины пространственного угла атака и угловой скорости. Предложен алгоритм установления диапазона допустимых величин переменных асимметрии космического зонда, гарантирующий спуск зонда в марсианской атмосфере без резонанса. Результатами вычислительного моделирования подтверждается обоснованность найденных ограничений с помощью представленной методики, наложенных на диапазон допустимых величин переменных асимметрий.