Методика оценки формы радиоотражающей поверхности крупногабаритного трансформируемого рефлектора космического аппарата

Методика исследования поведения радиоотражающей поверхности крупногабаритного трансформируемого рефлектора, находящегося под влиянием различных факторов космического пространства, включает в себя следующие этапы:

• -    определение отклонения поверхности рефлектора в пространстве от заданного положения;

• -    определение среднеквадратического отклонения поверхности от параболоида наилучшего соответствия.

Параболоид наилучшего соответствия (ПНС) – виртуальный параболоид с заданным значением фокусного расстояния, полученный в результате проведения нелинейного регрессионного анализа по методу наименьших квадратов применительно к массиву точек, описывающих радиоотражающую поверхность данного рефлектора. «Вписать» параболоид в радиоотражающую поверхность рефлектора – значит найти ПНС.

Задача «вписывания» ПНС в набор точек отражающей поверхности рефлектора, полученных в ходе проведения измерений, носит нелинейный характер и требует для решения применения численных методов оптимизации.

Анализ известных методов решения подобных задач, основанных на применении градиентных (метод градиентного спуска, метод Коши, метод Ньютона, метод Левенберга-Марквардта и др.), геометрических (метод поясов, метод касательных плоскостей), сто- хастических (метод Монте-Карло) и других подходов [1–3], автором статьи был выполнен, однако, к настоящему времени положительный результат получен лишь в случае применения алгоритма Левенберга-Марквардта.

Прежде чем перейти к рассмотрению алгоритма Левенберга-Марквардта, зададим функцию оптимизации, которая описывается уравнением параболоида, произвольно расположенного в пространстве.

Радиоотражающая поверхность рефлектора представляет собой круговую вырезку из параболоида вращения, смещенную вдоль оси Y , и описывается набором из N точек (рис. 1):

{ ( X. Y , Z ) } N , (1)

где X , Y , Z – координаты в канонической системе координат исходного параболоида.

Для каждой поверхности второго порядка существует декартова прямоугольная система координат, в которой эта поверхность имеет каноническое уравнение. Всего имеется 17 типов поверхностей второго порядка. Каждый тип характеризуется своим набором инвариантов и своей формой канонического уравнения – простейшей формой, к которой можно привести уравнение поверхности с помощью выбора декартовой прямоугольной системы координат. Соответст- вующие базис и система координат также называются каноническими [4].

Приведем уравнение поверхности второго порядка в общем виде [5]:

a 11 x ² + a 22 y ² + a 33 z ² + 2 a ₁₂ xy + 2 a 23 yz +

2 a 31 zx + 2 a ₁₄ x + 2 a 24 y + 2 a 34 z + a ₄₄ — 0,     (2)

Далее необходимо перейти от частного случая – канонического уравнения параболоида вращения (7), к общему случаю – уравнению поверхности второго порядка. Для этого представим уравнение (7) в матричном виде, и A , a и k , соответственно, будут равны:

где a ₁₁ , a ₂₂ , a ₃₃ , a ₁₂ , a ₂₃ , a ₃₁ , a ₁₄ , a ₂₄ , a ₃₄ , a ₄₄ – коэффициенты полинома.

Представим это уравнение в матричной форме:

A — 0

1 4 F

, a — [ — 1 0 0 ] , k — 0.

где

§ T A^ + 2 a^ + k — 0,

4 F

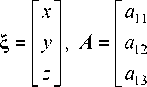
a 12

a 22

a 23

a 13

a 23

a 33

a — [ ^a 14    a 24    a 34 ] , k — a 44 .

Пусть в общем случае рассматриваемый параболоид имеет линейные и угловые отклонения от канонической формы. Запишем уравнение такого параболоида в канонической системе координат, используя матрицу перехода R . Конечное уравнение является уравнением поверхности второго порядка, произвольно ориентированной в пространстве, и имеет вид

Известно каноническое уравнение эллиптического параболоида [4]:

§ ' T A' ^ ' + 2 a' ^ ' — 0,                (9)

4 + Пг = 2Z. a2 P2

где

—

X — x Y — y

; A' — R ^T AR ; a' — aR .

где 9 , n , Z — неизвестные параметры уравнения; a , P - коэффициенты уравнения.

Для параболоида вращения это уравнение имеет вид

Z — z

— 2Z, a

где a — Р .

В выбранной системе координат уравнение (6) будет выглядеть следующим образом:

Y ² + Z ²             Y ² + Z' _v

---— = 2 X или -----= X , a ²               4 F

a ² где F —— 2

– фокусное расстояние.

Матрица перехода от старого базиса к новому в декартовой системе координат выражается с помощью комбинации трех углов, однозначно определяющих угловое отклонение нового базиса относительно старого. В качестве таких углов могут выступать углы Эйлера (угол нутации, угол прецессии, угол собственного вращения), самолетные углы (угол крена, угол рыскания, угол тангажа), углы поворота вокруг ортогональных осей. В рамках рассмотрения данной задачи удобнее всего воспользоваться матрицей перехода, являющейся матрицей поворота в трёхмерном пространстве относительно трёх координатных осей исходной системы координат. Такая матрица может быть получена, например, с использованием аппарата кватернионов [6] и имеет вид

R —

cos ( RZ ) cos ( RY )

cos ( RZ ) sin ( RY ) sin ( RX ) — sin ( RZ ) cos ( RX ) cos ( RZ ) sin ( RY ) cos ( RX ) + sin ( RZ ) sin ( RX )

sin ( RZ ) cos ( RY )                   — sin ( RY )

sin ( RZ ) sin ( RY ) sin ( RX ) + cos ( RZ ) cos ( RX ) cos ( RY ) sin ( RX ) sin ( RZ ) sin ( RY ) cos ( RX ) — cos ( RZ ) sin ( RX ) cos ( RY ) cos ( RX )

где RX , RY , RZ – углы поворота вокруг осей X , Y , Z соответственно в канонической системе координат.

Перейдем к алгоритму вписывания ПНС в набор точек радиоотражающей поверхности рефлектора.

Алгоритм Левенбрега-Марквардта предназначен для оптимизации параметров нелинейных регрессионных моделей и заключается в последовательном приближении заданных начальных значений к искомому локальному оптимуму [7].

Поскольку рассматриваемый параболоид имеет ось вращения (ось X ), то во избежание получения сингулярности в процессе выполнения алгоритма зада-

дим параметру RX значение, равное нулю. Тогда матрица перехода (11) примет вид

R (RY, RZ) — cos (RZ) cos( RY) sin (RZ) cos( RY)

—    — sin ( RZ )          cos( RZ )

cos ( RZ ) sin ( RY ) sin ( RZ ) sin ( RY )

— sin( RY ) 0 cos( RY )

Учитывая сказанное выше и уравнение (9), получаем функцию оптимизации, описывающую положение параболоида вращения в пространстве:

ParabFun ( X , Y , Z , to ) = ^ ' T A '^ ' + 2 a"^ , (13) где to = [ x y z RY RZ ] T – вектор параметров, определяющий линейные ( x , y , z ) и угловые ( RY , RZ ) отклонения параболоида вращения от канонической формы.

В качестве критерия оптимизации используется среднеквадратическая ошибка модели на заданной выборке:

N

^ ParabFun ( X, , Y_t , Z_t ,to)² ^ min. (14) i = 1

Для реализации алгоритма необходимо задать начальный вектор параметров ω . На каждом шаге итерации этот вектор заменяется на вектор ω + Δω [7]. Для оценки приращения Δω используется приближение функции:

ParabFun ( X , Y , Z , to + A to ) ®

® ParabFun ( X , Y , Z , to ) + J ( to ) A to ,

где J ( ω ) – якобиан функции ParabFun ( X , Y , Z ,ω) в точке ω :

J (to) = d ParabFun (X1, Y, Z1, to)

d to ₁

d ParabFun ( X 1 , Y , Z ₁, to )

d to ₅

d ParabFun ( X -, Y , , Z , , to )

d ParabFun ( X ,■ , Y , Z ,■ , to )

d to ₁

d to ₅

Путем несложных математических преобразований получим выражение [7; 8]:

Ato = ( J (to) T J (to)) J (to) T (Fun (to)), где

ParabFun ( X ₁, Y ₁, Z ₁, ω )

Fun ( to ) =

ParabFun ( X , Y , Z , ω )

Известно, что в процессе расчета матрица J ( to ) T J ( to ) может оказаться вырожденной. Во избежание этой проблемы американским математиком Дональдом Марквардтом в 1963 г. был введен параметр регуляризации X >  0 [7]:

A to ( to , X ) = ( J ( to ) T J ( to ) + X I ) J ( to ) T ( Fun ( to )), (19) где I = diag ( J ( to ) T J ( to ) ) . (20)

Блок-схема реализации данного алгоритма представлена на рис. 2.

В качестве примера, демонстрирующего работоспособность данного алгоритма, в таблице приведены результаты моделирования следующей ситуации:

– радиоотражающая поверхность рефлектора имеет линейные и угловые отклонения от заданного положения: x = 3, y = 4, z = 5; RY = 10°, RZ = 20°;

– смоделированы искажения формы поверхности вдоль соответствующих осей с использованием генератора случайных чисел: rnd_x = rnd (10^–4), rnd_y = = rnd (10^–4), rnd_z = rnd (10^–4).

В результате расчета, за 14-ти итераций были получены следующие величины отклонения ПНС от канонического вида:

x = 3,0000561311, y = 3,9999926509, z = 5,0000089952,

RY = 9,9999253282°, RZ = 20,0001102286° при заданной точности расчета s = 10-10.

Данный алгоритм был успешно протестирован на функции Розенброка путем нахождения локального минимума, что подтверждает его работоспособность. Результаты применения алгоритма приведены ниже:

• -    функция Розенброка:    RosenbrockFun ( x , y ) =

= (1 - x )² + 100( y - x 2 ) 2 ;

• -    начальное приближение: x ₀ = 0, y ₀ = 0 ;

• -    начальное значение параметра регуляризации: X^{< 0 >} = 10⁴;

• -    критерий останова: RosenbrockFun ( x , y ) < 10 ^{- 10};

• -    полученные значения переменных: x = 0,99999, y = 0,99998;

• -    теоретические значения переменных: x = 1, y = 1.

Следует отметить, что достигнутый результат был получен после 14 107 итераций (4,5 минуты машинного времени на рабочей станции средней вычислительной мощности). Есть сведения [8], что ответ может быть получен гораздо меньшим количеством итераций. Среди возможных причин продолжительности времени счета могут выступать:

• -    выбор начального приближения;

• -    выбор точности сходимости (критерий останова);

• -    выбор оптимального значения параметра регуляризации X^{< k >} на каждой итерации.

Результаты расчетов подтверждают, что применение алгоритма Левенберга–Марквардта позволяет вписать ПНС в деформированную радиоотражающую поверхность рефлектора с заданной точностью, определив его ориентацию в пространстве относительно канонической системы координат, что впоследствии даст возможность определить СКО смещенных точек радиоотражающей поверхности от ПНС и от теоретического профиля.

Вторым этапом исследования формы радиоотражающей поверхности рефлектора является определение среднеквадратического отклонения поверхности рефлектора от параболоида вращения, заданного в канонической системе координат. Процесс решения данной задачи складывается из трех шагов:

• -    задание функции оптимизации;

• -    определение расстояний от точек, описывающих радиоотражающую поверхность рефлектора, до канонического параболоида вращения с использованием метода Ньютона;

• -    определение СКО поверхности рефлектора от заданного канонического параболоида.

В качестве исходных данных для проведения расчета выступают координаты набора точек, описывающих радиоотражающую поверхность рефлектора, представленные системе координат, где параболоид, относительно которого будет определяться СКО, имеет канонический вид. Возможны несколько случаев расчета СКО: определение СКО от ПНС, определение СКО от теоретического параболоида.

Случай определения СКО от ПНС предполагает использование координат точек деформированной поверхности рефлектора с учетом компенсации ли- нейных и угловых отклонений, полученных в результате нахождения ПНС для этого набора точек.

В случае определения СКО от теоретического параболоида в рабочий алгоритм подставляются координаты точек, описывающих отражающую поверхность рефлектора, напрямую, т. е. без проведения дополнительных преобразований.

Как правило, чаще на практике используется случай определения СКО от ПНС, который будет рассмотрен далее подробно.

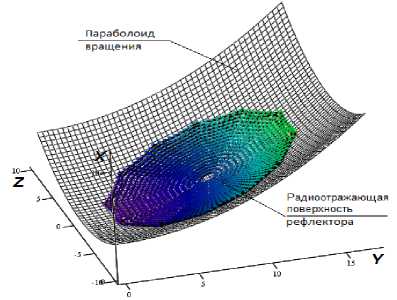
Рис. 1. Вписанный в реперные точки радиоотражающей поверхности рефлектора параболоид вращения (ПНС)

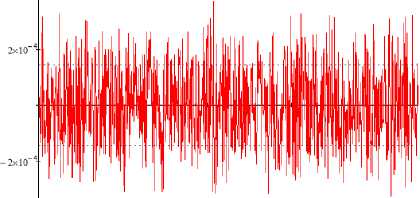
Рис. 3. Распределение отклонений от теоретического профиля по точкам радиоотражающей поверхности рефлектора

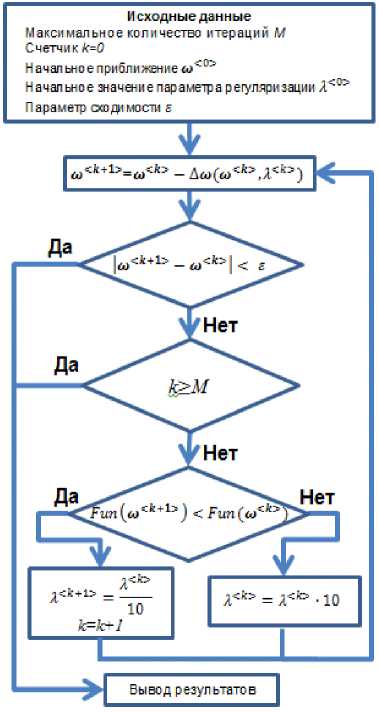
Рис. 2. Блок-схема рабочего алгоритма

Результаты расчета вписывания ПНС с помощью алгоритма Левенберга–Марквардта

k -я итерация	λ	x	y	z	RY	RZ	Fun ( ® < k + 1 > )	Fun ( w < k > )
1	1000	–0,0011948599	0,0014909484	0,0016262894	–0,0039098024	0,0037986940	210,1201250291	210,2041774599
2	100	–0,0071316546	0,0089152978	0,0097182097	–0,0233551297	0,0227057286	209,2839837966	210,1201250291
3	10	–0,0631473571	0,0803475632	0,0869840736	–0,2083777991	0,2039239828	201,3402218070	209,2839837966
4	1	–0,4079149817	0,5990569327	0,6055749061	–1,4196475550	1,4831749255	149,7480658534	201,3402218070
5	0,1	–0,6655363669	2,0997851510	1,0955996394	–2,5789538423	4,8664240291	73,9721366423	149,7480658534
6	0,01	1,2003978712	4,7815954855	–0,6217419735	–0,2597276959	10,.6774127514	35,0186490258	73,9721366423
7	0,001	2,4299822353	6,5642800231	–0,2966812952	–0,3672016584	13,0652873162	8,1905419796	35,0186490258

Окончание табл.

k -я итерация	λ	x	y	z	RY	RZ	Fun ( m < k + 1 > )	Fun ( w < k > )
8	0,0001	2,7665056851	6,0522450480	1,9462555051	3,4186857875	14,9695405943	3,.0576611878	8,1905419796
9	0,001	2,7665056851	6,0522450480	1,9462555051	3,4186857875	14,9695405943	3,0576611878	8,1905419796
10	0,0001	2,9235534072	5,3501917036	3,2264147489	6,1329317250	16,7740172665	1,7807514319	3,0576611878
11	0,00001	2,9661126934	4,2576111844	4,7644432566	9,4065361217	19,4122164073	1,6942318899	1,7807514319
12	0,000001	2,9984389607	4,0043735927	4,9975052637	9,9921857507	19,9898713652	0,0594100189	1,6942318899
13	1E-07	3,0000558761	3,9999977494	5,0000041911	9,9999140937	20,0000982549	0,0010684539	0,0594100189
14	1E-08	3,0000561311	3,9999926509	5,0000089952	9,9999253282	20,0001102286	0,0010683699	0,0010684539

Прежде чем перейти к рассмотрению метода Ньютона применительно к рассматриваемой задаче, зададим функцию оптимизации, которая должна описываться выражением, определяющим наикратчайшее расстояние от точки до поверхности параболоида.

Наикратчайшее расстояние от точки до поверхности – длина отрезка, лежащего на перпендикуляре, восстановленном из данной точки на касательную плоскость данной поверхности. Нахождение этой величины является оптимизационной задачей.

Как известно, расстояние от точки P (x0; у0; z0) до плоскости

Plane = A x + B у + C z + D определяется по выражению g = A x о + B у о + C z о + D J A2 + B2 + C2

Уравнение касательной плоскости имеет вид

— ( X - x ) + — ( Y - у ) + — ( Z - z ) = 0. (23) d x^{v 7} dp ⁷ d z^{v 7}

Из выражений (22) и (23) следует, что уравнение касательной плоскости для точки, лежащей на поверхности параболоида будет иметь вид

YZ

(-1) (X - x)+—(Y - y)+—(Z - z ) = 0.

Тогда формулу для определения расстояния от точки, принадлежащей радиоотражающей поверхности рефлектора, до касательной плоскости, проходящей через точку Pparab, лежащую на поверхности теоретического параболоида, можно записать как дачи поиска минимума расстояния от точки на поверхности рефлектора до рассматриваемого параболоида по методу Ньютона:

DistFun ( у, z, X, Y, Z ) = S .          (26)

Метод Ньютона – итерационный численный метод нахождения корня заданной функции [8]. Алгоритм нахождения численного решения уравнения DistFun ( у, z, X, Y, Z ) = 0 сводится к итерационной процедуре вычисления:

у_к + i, i = у к , i -_ ^z k + 1, / J L z k , i _

• ^- ( v ^{2 DistFun (} у к , i , z k , i , X i , ^Y , ^Z i ) ) ¹ X

XV DistFun ( у_к , i , z_k , i , X i , Y i , Z i ),        (27)

где i – номер рассматриваемой точки на поверхности рефлектора; k – номер итерации.

Критерий останова при выполнении алгоритма:

DistFun ( у_к , i , z k , i , X i , ^Y i , ^Z i ) ^-

• ^{- DistFun} ( у_к + 1, i , z k + 1, i , X i , ^Y , ^Z i ) < 6 ,     ⁽²⁸⁾

где ε – точность сходимости.

Значения отклонений точек от рассматриваемого параболоида представлены на рис. 3, где ось абсцисс – номер точки радиоотражающей поверхности рефлектора, ось ординат – величины отклонений каждой точки от рассматриваемого параболоида.

Среднеквадратическое отклонение точек на радиоотражающей поверхности рефлектора от теоретического профиля рассчитывается по выражению

YZ

^{( - 1) (} X - x ^{) +}yx( ^{Y -} y ^{) +}x^( ^{Z - z} ) g =____________ 2 F _________ 2 F _______

,

. ( - 1)² +1 — I +1 — I

V 1 2 F I I 2 F I

RMS =

^ i = ₁ (^g ( ^у к + 1, / , z k + 1, / , ^X i , ^Y i , ^Z i ) )

N

2     2

у + z где x =------

4 F

; точка P_parab ( x , y , z ) принадлежит пара-

болоиду.

Аналогично действиям, применимым к алгоритму Левенберга–Марквардта, и на основании выражения (25) зададим функцию оптимизации для решения за-

Использование метода Ньютона позволяет определить среднеквадратическое отклонение точек радиоотражающей поверхности рефлектора от параболоида наилучшего соответствия, а также от теоретического параболоида.

Разработанный алгоритм с использованием метода Ньютона применим для рефлекторов с любой возможной степенью искажения радиоотражающей поверхности.

Таким образом, разработанная методика, включающая в себя определение параболоида наилучшего соответствия и СКО поверхности рефлектора, позволяет определить основные геометрические характеристики данного рефлектора. Методика может быть использована при обработке результатов опытных и натурных исследований. В настоящее время ведется работа по созданию методики управления формой радиоотражающей поверхности рефлектора в процессе его эксплуатации на орбите.