Методика оценки эффективности применения аэрозольных образований для защиты объектов от прицельной стрельбы из гранатомета

Цитирование: Козирацкий, Ю.Л. Методика оценки эффективности применения аэрозольных образований для защиты объектов от прицельной стрельбы из гранатомета / Ю.Л. Козирацкий, Д.В. Прохоров // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(7). С. 882–893. DOI: 10.17516/1999-494X-0274

пределенности, обусловленной наиболее вероятным нахождением ее по представлению стрелка. Стрельба при этом будет осуществляться по памяти, в направлении шума мотора или лязга гусениц [6], опираясь на какие-либо визуальные ориентиры. Ввиду высокой плотности завесы и значительных флуктуаций коэффициента пропускания аэрозольного образования [1-4] такими ориентирами для стрелка могут стать контрастные выбросы, обусловленные флуктуациями АО. Вследствие случайного характера этих выбросов точка прицеливания (ТП) стрелка также будет формироваться по случайному закону с ошибками, обусловленными опытностью и памятью стрелка, а также флуктуационными свойствами АО. Геометрия задачи представлена на рис. 1. Будем считать также, что стрельба осуществляется одним стрелком (последовательно)

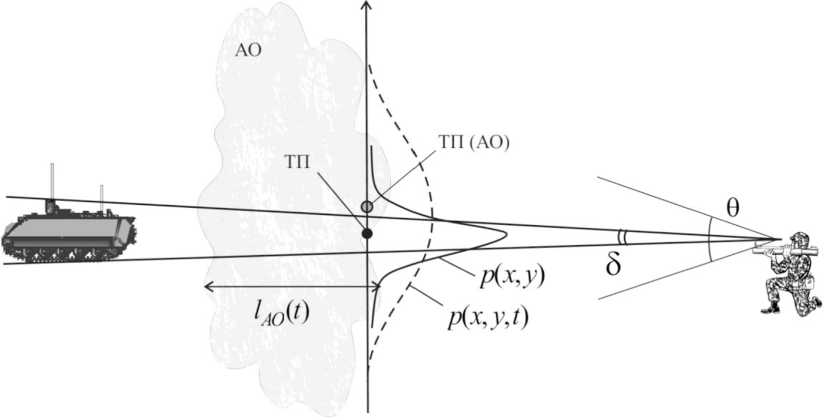
Рис. 1. К постановке задачи

Fig. 1. To the problem statement по цели, полностью прикрытой аэрозольным образованием, пропускные свойства которого изменяются со временем – можно выделить этапы формирования, существования и рассеивания АО [3]. В качестве показателя эффективности ведения стрельбы примем вероятность попадания снаряда в цель Pn.

Моделирование процесса стрельбы

Динамику процесса стрельбы можно представить в виде ориентированного графа состояний, показанного на рис. 2, где приняты следующие обозначения: С1 – исходное состояние; С2 – состояние, при котором в результате выстрела из гранатомета снаряд попал в цель; С3 – состояние, при котором в результате выстрела из гранатомета снаряд не попал в цель. Принятие решения о попадании или непопадании снаряда в цель может осуществляться по дополнительно проявляющимся после выстрела признакам, например по звуку взрыва.

Каждый из переходов из состояния i в состояние j будет характеризоваться вероятностью и плотностью вероятности перехода P_i j , φ_i j ( t ).

В соответствии с рекомендациями, изложенными в [7], представим динамику рассматриваемого процесса в форме передаточных функций (рис. 3).

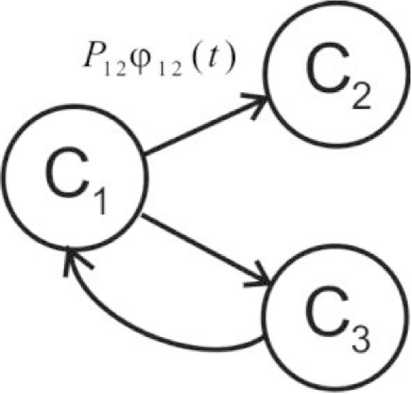
Рис. 2. Граф состояний

Fig. 2. State graph

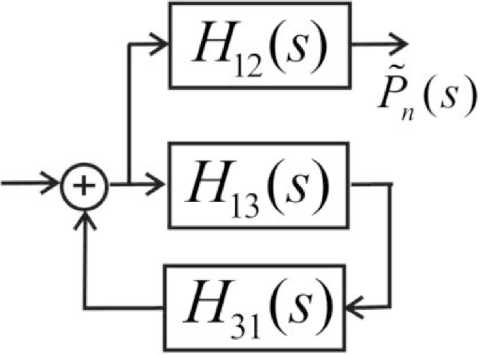
Рис. 3. Процесс стрельбы в форме передаточных функций

Fig. 3. Shooting process in the form of transfer functions

H ij ( s ) = Ls[ P ij φ ij ( t )] – передаточная функция, представляющая собой преобразование Лапласа от произведения вероятности перехода на плотность вероятности времени перехода из состояния i в состояние j .

Используя схему на рис. 3, производя в соответствии с методами теории автоматических систем [8] несложные математические преобразования, можно записать следующее выражение для определения передаточной функции процесса стрельбы:

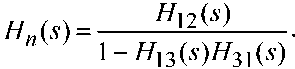
Введем в рассмотрение цикличность стрельбы, состоящую из n итераций. Применение к (1) Z-преобразования дает [7]

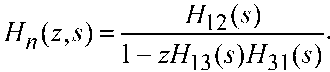
С учетом циклов по n можно записать

H,Ms) = Hi2(s)Vhii№*<. (3)

Тогда вероятность события, состоящего в том, что стрелком к некоторому моменту времени t будет совершено ровно n выстрелов и произойдет попадание в цель, можно записать следующим образом:

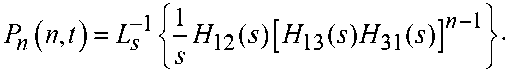
Вероятность попадания в цель в зависимости от числа прицельных выстрелов n по ней одним стрелком однотипным оружием можно получить с использованием выражения

p_ri^^= £ ^pnM 77=1

Для случая, когда плотности вероятности распределения времени нахождения в одном состоянии при переходе в другое состояние определяются экспоненциальными распределениями, передаточные функции переходов можно записать следующим образом:

MW,.-^ ; ^Т')^--^::^; H ,, ( 5 ) = 1,            (6)

S + /tp                   S + Д^

где X 1з = X ₁₂ — интенсивности стрельбы.

Интенсивность стрельбы связана со средним временем стрельбы обратной зависимостью [9].

Для определения среднего времени стрельбы можно воспользоваться подходом, описанным в [9].

Среднее время стрельбы будет обусловлено в основном средним временем подготовки оружия к стрельбе, средним временем принятия решения о наличии цели и направлении стрельбы в сложных условиях обстановки, средним временем прицеливания и средним временем полета ^снаряда Тр2 ~ ^подг + ^Тпрн + ^пр + .цс

При определении средних времен и переходных вероятностей P ₁₂ и P ₁₃ = 1 — P ₁₂ ( P ₃₁ = 1) необходимо учитывать следующее допущение двух ситуаций, когда стрелок потенциально может увидеть цель (этапы формирования или рассеивания АО) и когда цель визуально обнаружена быть не может (АО сформировано). Во втором случае определение направления стрельбы осуществляется на основе априорной информации о цели, полученной до постановки АО, ориентированием стрелка по шуму техники (на ее акустическое излучение), по формируемому в поле зрения изображению АО.

Определение вероятности попадания в цель

Вероятность попадания в цель можно определить как

Рц = Р„0^ = Р, Д/У,₄„,Д-У^.                 (7)

где Р_подг(t) - вероятность подготовки оружия к стрельбе в зависимости от времени; Р прнподг (t) -условная вероятность принятия решения о наличии цели (обнаружение) или направлении стрельбы в условиях, когда цель не видна из-за АО, в зависимости от времени;

^Р прн/подг ^{( t )    Р} обн^{( t} ), ^при t ≤ необ ;

Рпрн/подг (t)   Рнапр(t), при t > Н оеоб, где Робн(t) - вероятность обнаружения цели в зависимости от времени; Рнапр(t) - вероятность принятия решения о направлении стрельбы в условиях постановки АО в зависимости от времени; Тнеоб - среднее время принятия решения стрелком о необнаружении цели; Рпр1прн(t) - условная вероятность прицеливания и попадания в цель в зависимости от времени.

Определение условной вероятности Р прнподг ( t ) возможно с использованием формул Бейеса и полной вероятности [11].

Для случая формирования гипотез H1 (стрелок определил направление стрельбы по цели в результате ее обнаружения) и H2 (стрелок определил направление стрельбы по цели наугад (цель не обнаружена)), а также рассмотрения события А, заключающегося в том, что за время принятия решения о направлении стрельбы стрелок определит направление стрельбы по цели, можно записать следующее выражение:

P npHlnodr ( t ) = Р обн Р ( H 1 A ) + Р напр Р ( H ₂| A ),

где

P^PW+P^PtHp

;

P„„pP(HA

P<,6„P№+P„„pP(H2)

— апостериорные веро

ятности гипотез; P ( H 1 ) и P ( H ₂) — вероятности гипотез.

Условную вероятность прицеливания и попадания в цель получим из следующих соображений.

Ошибки прицеливания, неоднообразные прикладка и удержание оружия, различные метеоусловия обуславливают ошибки выстрелов и вызывают рассеяние точек попадания [5]. Распределение точек попадания при ведении прицельной стрельбы по цели обычно характеризуют нормальным законом распределения [10]. При этом математические ожидания и средние квадратические отклонения (СКО) координат точек попадания ввиду вышеуказанных факторов будут нестационарными величинами и обуславливаться, например, сносом АО и изменением наблюдаемого стрелком фонового изображения ввиду флуктуаций АО, опытностью и памятью стрелка.

Тогда двумерную плотность вероятности распределения координат точек попадания х и у как функцию времени можно записать как [11]

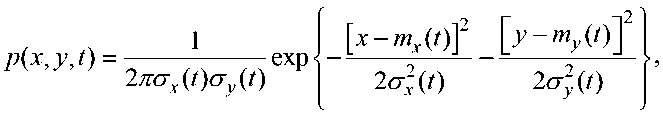
где m_x(t ), m y (t ) — математические ожидания координат точек попадания как функции времени; о_х ( t ), o y ( t ) — средние квадратические отклонения координат точек попадания в зависимости от времени; <7^/) = ^сг^Тс^ о_пр — ошибка прицеливания; o n — ошибка, обусловленная опытностью и памятью стрелка; σ_a – ошибка, обусловленная ориентированием стрелка по шуму техники (на ее акустическое излучение); о му (t ) — ошибка, обусловленная метеоусловиями, флуктуационными свойствами АО; для о y (t ) можно раскрыть аналогично.

С учетом «фигурности» реального объекта поражения (цели) условная вероятность прицеливания и попадания в цель в условиях ее прикрытия АО может быть записана следующим образом [11]:

Р„р„рн ^ = ^Кф^ P(x,y,t)dxdy , ⁽¹¹⁾

где К ф = S_ц / S on — коэффициент фигурности [5]; S_ц — площадь цели; S on = х ц у ц — площадь описанного вокруг цели прямоугольника; х ц и у ц — размеры цели по горизонтали и вертикали соответственно.

Учет влияния нестационарного аэрозольного образования на процесс визуального обнаружения стрелком цели

Предположим, что постановка АО осуществлена в момент подготовки стрелка к выстрелу.

Изменение пропускных для оптического излучения свойств среды принято характеризовать коэффициентом пропускания, определяемым показателем ослабления k и оптической толщей l_AO , которая будет изменяться со временем (рис. 1) [1, 2, 12] T ( t ) = exp[— k "  l_AO ( t )].

Как показано в [13], для случайного визуального просмотра заданного сектора поиска характерна экспоненциальная зависимость вероятности обнаружения от времени. При этом ввиду необходимости учета влияния нестационарных аэрозольных маскирующих помех можно воспользоваться результатами, полученными в [2, 3, 9].

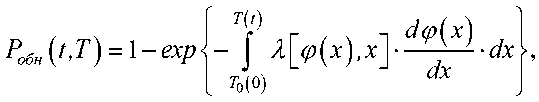
где X [ ф ( x ), x ] — интенсивность поиска, как функция времени и коэффициента пропускания; ф(Т ) - функция, обратная f t) ) (t = ф(Т ), Т t = 1/[ dф(Т)/dT ]).

Выражение (12) представляет собой зависимость вероятности обнаружения цели от времени при случайном просмотре сектора поиска с учетом интенсивности поиска и задаваемого закона изменения коэффициента пропускания аэрозольного образования.

В процессе этапов формирования, существования и рассеивания АО, прикрывающего цель, стрелок перед каждым последующим выстрелом будет осуществлять процедуру поиска цели. Тогда с учетом параметров АО (Y1 и Y3 — интенсивности формирования и рассеивания АО; То и Tmin — максимальное и минимальное значения коэффициента пропускания АО; t1 и t2 — моменты времени существования АО) выражения для определения вероятностей обнаружения цели к моменту времени t для случаев ведения поиска на этих этапах запишем следующим образом:

1) для этапа формирования t < t 1

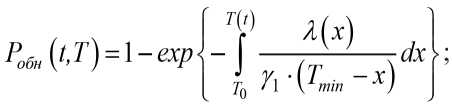
2) для этапа существования t 1 <  t < t ₂

;

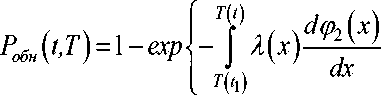
3) для этапа рассеивания t >  1 ₂

Робн^Л^-^Р'

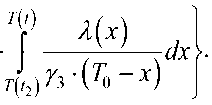
Выражение для определения интенсивности случайного визуального поиска получим, используя [13].

Предположим, что изначально в исходном состоянии стрелку уже известно местоположение цели и ему необходимо подготовиться, прицелиться и выстрелить. Учитывая возникшие в результате постановки АО сложные условия наблюдения, стрелок перед каждым выстрелом вынужден осуществлять поиск цели, находящейся в некоторой области неопределенности, обусловленной наиболее вероятным нахождением ее по представлению стрелка. Сектор поиска в этом случае значительно сужается. Поиск и прицеливание могут осуществляться с помощью прицельной планки (невооруженным глазом) или оптического прицела. На типовых дально- стях применения гранатомета поле зрения оптического прицела соизмеримо с полем поиска, поэтому процедура поиска может осуществляться без сканирования прицелом (поиск будет осуществляться в поле зрения оптического прицела глазом стрелка или невооруженным глазом в равнозначном поле поиска через прицельную планку).

Интенсивность случайного поиска невооруженным глазом протяженного одиночного неподвижного объекта можно определить следующим образом [13]:

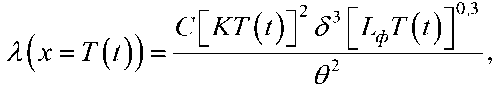
где С - коэффициент, характеризующий индивидуальные способности наблюдателя (для монокулярного зрения - С м = 12 град² угл. мин^-3(кд/м²)^-0,3с^-1); К = ( Ъ ф - Ъ о ) / Ъ ф - яркостный контраст объекта; Ъ ф и Ъ о - яркости фона и объекта [кд/м²]; б - угловой размер объекта [угл. мин]; θ – угловой размер поля поиска [град].

При поиске в оптический прицел яркость фона, угловой размер объекта и контраст рассчитывают по формулам [13]: Ъ ф = т о Ъ ф ; д' = Гб ; К' = К / (1 + q ), где т о - коэффициент светопро-пускания; Г – увеличение оптического прицела; q – коэффициент светорассеяния.

Среднее время принятия решения о наличии цели и направлении стрельбы в условиях нестационарной аэрозольной маскирующей помехи с вероятностью Р_о5н (т„_ео5 ) может быть определено следующим образом:

, при          ;

, при

где

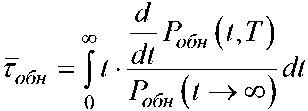
– среднее время принятия решения об обнаружении цели с вероятностью Робн (тнеоб )

Результаты апробации методики

С целью апробации предлагаемой методики были произведены расчеты для следующих исходных данных: начало системы координат совпадает с центром цели; размеры цели x ц = 3 м; у ц = 2 м; К ф = 0,83; a x = a y = 0,5 м; на дальности порядка 200 м б = 42 угл. мин.; Ъ ф = 30 кд/м²; К = 0,17; поле зрения оптического прицела в = 13 град; Г = 2,7; q = 0,05; т о = 0,6; f₁₂ = 12 с (средняя скорострельность РПГ-7 составляет 5 выстрелов/мин.); P подг = 0,98; P пр|прн = 0,79; P напр = 0,14; ^тнеоб = 4 с; Y i = 2,8 с^-1; у₃ = 0,1 с^-1; Т ₀ = 0,95; T min = 0,004; 1 1 = 3 с; t ₂ = 32 с; время постановки АО -2,8 с.

На рис. 4 представлены графики зависимости условной вероятности прицеливания и попадания боеприпаса в цель в некоторый момент времени t ₀ Р прпрн (t₀,a x ) (в соответствии с выражением (10)) от ошибок прицеливания по оси х для различных значений нестационарных m x ( t ), m y ( t ).

На рис. 5 представлены результаты расчетов зависимости вероятности обнаружения цели невооруженным глазом и через оптический прицел от времени для трех этапов существования АО. Анализ полученных результатов показывает, что на этапе формирования АО при некоторых исходных данных может возникать ситуация, когда обнаружение цели стрелком осуществляется практически мгновенно с вероятностью, близкой единице. Это объясняется – 889 –

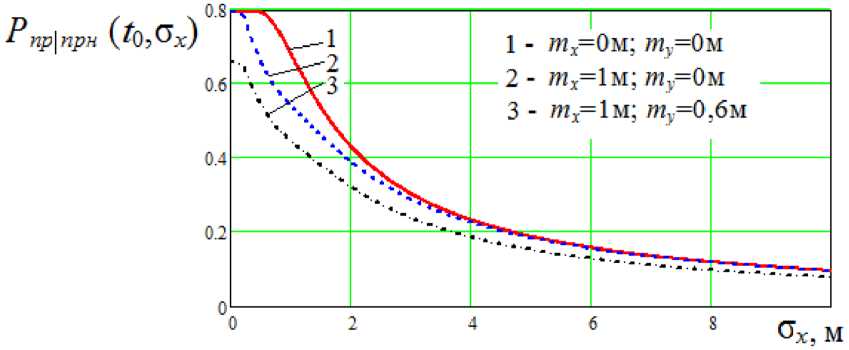
Рис. 4. Графики зависимости условной вероятности прицеливания и попадания боеприпаса в цель от ошибок прицеливания по оси х в момент времени t 0

Fig. 4. Dependence plots of conditional aiming probability and ammunition hitting the target from aiming errors along the x-axis at the time t 0

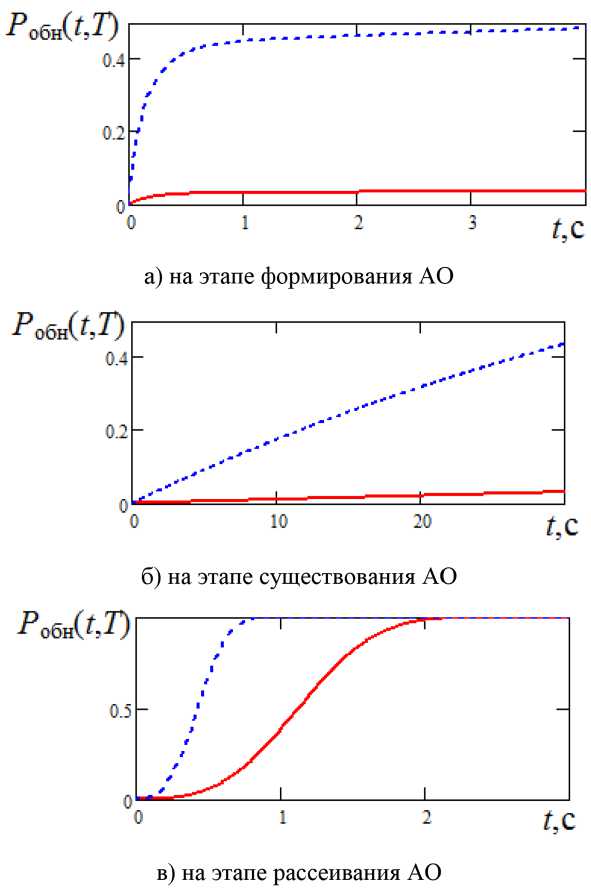
Рис. 5. Графики зависимости вероятности обнаружения цели невооруженным глазом (–) и через оптический прицел (– –) от времени для трех этапов существования АО

Fig. 5. Target detection probability graphs with the naked eye (–) and through the telescopic sight (– –) from time to time for three stages of existence AF тем, что поле поиска практически совпадает с полем зрения прицела, а в случае с оптическим прицелом – еще и с увеличением видимых размеров объекта. Поэтому время обнаружения в этом случае может ограничиваться временем реакции глаза человека (порядка 0,1–1 с [13]). В представленном случае вероятность обнаружения к моменту времени ^необ = 4 с не превышает 0,035 и 0,485 для поиска невооруженным глазом и через оптический прицел соответственно.

На втором этапе существования АО ( t 1 ≤ t <  t 2 ) обнаружение цели как невооруженным глазом, так и через оптический прицел возможно с малой вероятностью. На третьем этапе среднее время обнаружения при указанных исходных данных составило 1,27 и 0,49 с невооруженным глазом и через оптический прицел соответственно.

В соответствии с выбранным показателем и полученным для его определения выражением (4) построены графики зависимости вероятности попадания n -м выстрелом в цель от времени (рис. 6) и график распределения финальной вероятности того, что при совершении ровно n выстрелов произойдет попадание в цель (рис. 7). Анализ результатов показывает, что в интервалы времени, когда АО еще не сформировано или рассеивается, вероятность попадания существенно выше.

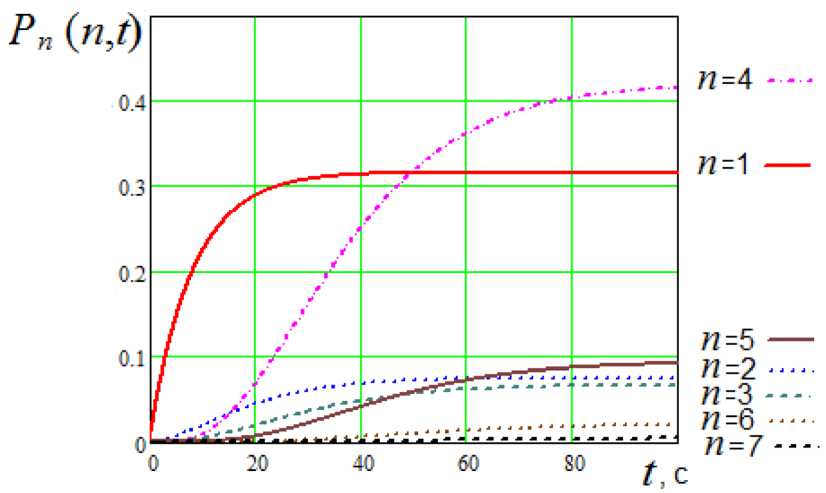
Рис. 6. Графики зависимости вероятности попадания n -м выстрелом в цель от времени

Fig. 6. Graphs of the dependence of the probability of hitting the target with the n -th shot on time

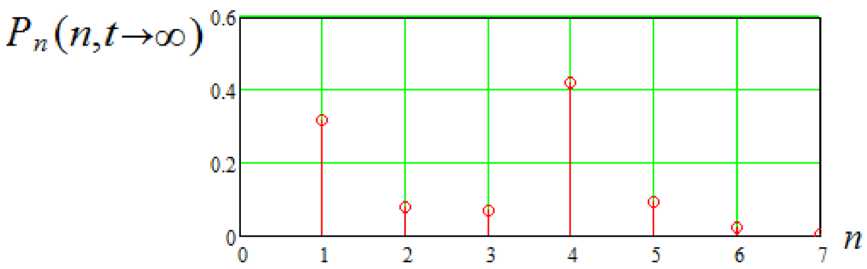
Рис. 7. График распределения финальной вероятности того, что при совершении ровно n выстрелов произойдет попадание в цель

Fig. 7. The graph of the distribution of the final probability of that when exactly n shots are fired, the target will be hit

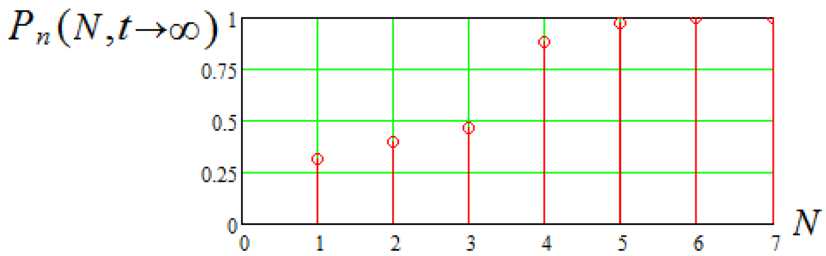
Рис. 8. График распределения финальной вероятности попадания в цель от числа выстрелов

Fig. 8. The graph of the distribution of the final probability of hitting the target on the number of shots

На рис. 8 представлена зависимость финальной вероятности попадания боеприпаса в цель от числа прицельных выстрелов по ней одним стрелком, однотипным оружием в условиях прикрытия цели нестационарным аэрозольным образованием.

Анализ полученных результатов показывает адекватность разработанной методики изменяемым исходным данным (в том числе нестационарным числовым характеристикам координат точек попадания боеприпаса, обусловленным совокупностью вышеописанных факторов).

Заключение

Таким образом, с использованием теории графов, теории вероятностей, методов преобразования Лапласа разработана методика оценки эффективности применения аэрозольных образований для защиты объектов от прицельной стрельбы из гранатомета. Методика позволяет получать вероятностные показатели попадания снарядов в цель при стрельбе из гранатомета в сложных условиях обстановки с учетом временных характеристик процесса стрельбы и совокупности ошибок прицеливания, обусловленных рядом факторов, в том числе применением аэрозольных завес. Использование математического аппарата производящих функций позволило определить вероятностные показатели процесса стрельбы с учетом цикличности, обусловленной количеством выстрелов по цели.