Методика оценки рисков утери конфиденциальной информации в компании

Бытует мнение, что управление рисками -удел топ-менеджеров либо сотрудников специализированных подразделений, риск-менеджеров, аналитиков. Однако на деле все обстоит по-иному. Регулирование, а тем более оценка рисков являются прикладными задачами. И сфера информационной безопасности (ИБ) - не исключение. Специалисты в области ИБ должны скрупулезно отслеживать возникающие угрозы, анализировать связанные с ними риски и представлять руководству уже готовый отчет-план, какими средствами бороться за сохранность корпоративных данных.

Анализ рисков в области ИБ может быть качественным и количественным. Количественный анализ позволяет получить конкретные значения рисков, но он отнимает заметно больше времени, что не всегда оправданно. Чаще всего бывает достаточно быстрого качественного анализа, задача которого - распределение факторов риска по группам. Шкала качественного анали- за может различаться в разных методах оценки, но всё сводится к тому, чтобы выявить самые серьезные угрозы [1]. В настоящей работе мы рассмотрим методику, использующую качественный анализ.

Методика оценки рисков состоит из следующих этапов: обработка выборки экспертов, анализ оценок, полученных в ходе опроса, и, на основе полученных результатов, формирование рекомендаций для лица, принимающего решения.

Вопросы, задаваемые экспертам относительно ряда категорий конфиденциальных сведений, делятся на две группы. Ответы на вопросы первой группы даются в виде оценок в баллах от 0 до 10, которым могут быть сопоставлены вероятностные характеристики. Ответы на вопросы второй группы даются в виде денежных оценок

Суть математической обработки данных, полученных в ходе ответов экспертов на вопросы первой группы, сводится к определению, насколько эксперты едины в своих вероятностных оценках относительно каждого вопроса по каждой категории конфиденциальных сведений.

Рассмотрим подробнее процедуру математической обработки данных для первой группы вопросов.

В исследуемой группе присутствуют следующие вопросы.

• 1.    Степень важности неразглашения конфиденциальных сведений.

• 2.    Вероятность использования конфиденциальной информации злоумышленником (утрата конфиденциальности).

• 3.    Вероятность появления кризисной ситуации в случае использования конфиденциальной информации злоумышленником.

• 4.    Вероятность появления кризисной ситуации в случае утраты конфиденциальных сведений.

• 5.    Вероятность модификации и искажения конфиденциальных сведений.

• 6.    Вероятность появления кризисной ситуации в случае модификации и искажения конфиденциальных сведений злоумышленником.

• 7.    Вероятность нарушения процесса, связанного с данным видом конфиденциальных сведений.

• 8.    Вероятность быстрого восстановления процесса после потенциальной кризисной ситуации.

• 9.    Актуальность обеспечения защиты данных конфиденциальных сведений через три года.

Допустим, что мы имеем k ответов n экспертов на некоторый вопрос из перечисленных выше для некоторой категории конфиденциальных сведений.

Обозначим ответы экспертов как Y _k , где k меняется от 1 до n .

Оценим математическое ожидание ответа эксперта на вопрос – среднее арифметическое по всем ответам Y _k . Суммируем все Y _k и делим на n : ⁿ

Y = - Z Y k .             (1)

n k = 1

Далее находим центрированную оценку для каждого ответа. Для этого вычитаем оценку «математическое ожидание» из к а ждого Y _k :

У к = Y k — Y .               (2)

Просуммировав полученные центрирован- ные оценки каждого ответа, возведенные в ква-

драт, и поделив эту сумму на (n – 1), получаем оценку несмещенной дисперсии: n d=A Z ук.

n - 1 к = 1

Обозначим буквой σ квадратный корень из

дисперсии:

C = 45.              (4)

Величина C - несмещенная оценка среднеквадратичного отклонения – показывает, на- сколько совпадают ответы экспертов на вопрос. Чем C меньше, тем большее единодушие демонстрируют эксперты при даче вероятностной оценки по данному вопросу. И наоборот, чем больше с, тем больше разброс в оценках экспертов по данному вопросу.

Оценка математического ожидания Y ± C дает нам интервал средней вероятностной оценки экспертов для данного вопроса.

Для каждого математического ожидания может быть построен доверительный интервал:

ГТ — ГТ Л

I Y -    t c , Y + И           (5)

V V n V n )

по уровню значимости α . Стандартным значением параметра α является 0,05, что соответствует мере надёжности 0,95. Это означает, что с вероятностью 95% математическое ожидание окажется в доверительном интервале. Параметр t _c определяется как двусторонняя квантиль:

t c = t( a , n - 1)                  (6)

из распределения Стьюдента по таблице 1.

Таблица 1

Число степеней свободы j	t (0,05; j )
4	2,78
5	2,57
6	2,45
7	2,36
8	2,31
9	2,26
10	2,23
11	2,20
12	2,18
13	2,16
14	2,14
15	2,13

Вместо таблицы можно воспользоваться эмпирической формулой:

t c = 3,93689 - 0,419522 j +

+ 0,0351859 j ² - 0,00102305 j ³.

Можно проверить гипотезу о значимости выборочной средней. Для этого рассчитаем контрольный параметр H :

H = Y—.(7)

C

Если параметр H по модулю больше t _c :

|H > tc, то на поставленный вопрос следует дать положительный ответ, в противном случае:

| H < tc(9)

• – отрицательный.

Основываясь на результатах обработки данных, лицо, принимающее решение, может сделать вывод по каждому из перечисленных вопросов.

Пример. Пусть имеется группа экспертов, состоящая из 15 респондентов. Результатом опроса этой группы являются 15 ответов на первый вопрос одной из категорий конфиденциальной информации.

Обозначим ответы экспертов как Y_k , где k меняется от 1 до 15 (таблица 2).

Таблица 2

Номер ответа	Ответ
Y 1	8
Y 2	0
Y 3	1
Y 4	0
Y 5	0
Y 6	2
Y 7	1
Y 8	10
Y 9	9
Y 10	8
Y 11	10
Y 12	2
Y 13	1
Y 14	0
Y 15	0

Находим оценку математического ожидания

ответа эксперта на вопрос, то есть среднее ариф- метическое по всем ответам Yk. Суммируем все Yk и делим на 15:

n               15

Y = ¹ S y = — У Y = ⁵² = 3,467. n ^У k 15^y k 15

Далее находим центрированную оценку для каждого ответа. Для этого вычитаем оценку математического ожидания из каждого Y_k (таблица 3).

Таблица 3

Номер ответа	Ответ	yk
Y 1	8	4,533
Y 2	0	–3,467
Y 3	1	–2,467
Y 4	0	–3,467
Y 5	0	–3,467
Y 6	2	–1,467
Y 7	1	–2,467
Y 8	10	6,533
Y 9	9	5,533
Y 10	8	4,533
Y 11	10	6,533
Y 12	2	–1,467
Y 13	1	–2,467
Y 14	0	–3,467
Y 15	0	–3,467

Просуммировав полученные центрирован- ные оценки каждого ответа, возведенные в квадрат, и поделив эту сумму на (n – 1), получаем оценку несмещенной дисперсии:

n

D = А У y k = n - 1 k ~ T

15 - 1

45, ₂ _ 239,733

^У y^k    14

k _ 1            ¹⁴

_ 17,123.

Обозначим буквой Т квадратный корень из оценки дисперсии:

т _ V DD _ V 17,123 _ 4,138.

Поскольку значение Т достаточно велико, то можно сделать вывод, что оценки экспертов по данному вопросу неоднозначны, так как интер-

(      Т          Т I вал Y ± т имеет вид I Y —3=tc, Y + —j=tc I.

V   Vn       Vn )

Для каждого математического ожидания по- строим доверительный интервал:

Y - -^ t ., n

т tc n

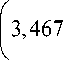
4,138

t c , 3,467 +

4,138 1 ^

715 ^c )

по уровню значимости α . Стандартным значением параметра α является 0,05, что соответствует мере надежности 0,95. Это означает, что с вероятностью 95% математическое ожидание окажется в доверительном интервале. Параметр t_c определяется как двусторонняя квантиль:

t_c _ t( a , n - 1) _ t (0,05; 14)

из распределения Стьюдента, в описываемом случае оно равно 2,14. Таким образом, для найденного ранее математического ожидания доверительный интервал будет следующим: (1,18; 5,75).

Далее проверим гипотезу о значимости выборочной средней. Для этого рассчитаем контрольный параметр H :

H _ Y— _ 3,245. т

Так как параметр H по модулю больше tc, то на поставленный вопрос следует дать положительный ответ, т.е. математическое ожидание от- лично от нуля.

Найденная несмещенная оценка среднеквадратичного отклонения описывает меру рассеяния. Если она велика, то необходимо провести кластерный анализ. В случае если мера рассеяния несущественна, то вся выборка будет составлять одну группу.

Проблема кластерного анализа – обоснование и построение наилучшего «по сходству» (в том или ином смысле) разбиения исходного множества объектов. При этом к каждому кластеру будут отнесены объекты, имеющие характерную общность, сами же кластеры имеют существенные различия. Понятие о наилучшем разбиении уточняется в каждой конкретной задаче путем выбора критерия оптимальности разбиения (построения кластеров), отражающего «сходство» элементов, отнесенных к данному кластеру.

Существует множество методов кластерного анализа. Рассмотрим наиболее распространенный – метод древовидной кластеризации.

Метод древовидной классификации – это пошаговый метод разбиения выборки на отдельные группы. Его принцип достаточно прост.

Шаг 1. Каждый человек признается единственным представителем своего кластера (типа). Количество типов равно объему выборки.

Шаг 2. Находится несколько человек, которые наиболее похожи на первого. Теперь эти люди составляют один кластер. Количество кластеров уменьшается.

Шаг 3. Продолжаем искать кластеры, наиболее похожие друг на друга, и объединять их. Теперь вся выборка разделена на некоторое количество групп, внутри которых люди очень схожи по своим характеристикам. Это продолжается, пока объединение не закончится и наступит последний шаг.

Шаг 4. Вся выборка объединяется в один кластер. Этот шаг не является информативным, так же как и первый шаг, но неизбежен в связи с процедурой. [2]

Пример. Рассмотрим группу экспертов, состоящую из 15 экспертов, результаты опроса которых указаны в таблице 2. Проведем кластерный анализ. В качестве математического критерия кластеризации возьмем меру расстояния между ответами экспертов.

Шаг 1. У нас имеется 15 кластеров.

Шаг 2. Кластер 1: Y ₁, Y ₁₀.

Шаг 3. Кластер 2: Y ₂, Y ₄, Y ₅, Y ₁₄, Y ₁₅.

Кластер 3: Y ₃, Y ₇, Y ₁₃.

Кластер 4: Y ₆, Y ₁₂.

Кластер 5: Y ₈, Y ₁₁.

Кластер 6: Y ₉.

Наиболее близкие по значениям кластеры 1, 5, 6 и кластеры 2, 3, 4, поэтому объединяем их.

Кластер 1: Y ₁, Y ₁₀, Y ₈, Y ₁₁, Y ₉.

Кластер 2: Y ₂, Y ₄, Y ₅, Y ₁₄, Y ₁₅, Y ₃, Y ₇, Y ₁₃, Y 6 , Y 12 .

Шаг 4. Кластер 1: Y ₁, Y ₁₀, Y ₈, Y ₁₁, Y ₉, Y ₂, Y ₄, Y ₅, Y 14 , Y 15 , Y 3 , Y 7 , Y 13 , Y 6 , Y 12 .

Итогом кластеризации будет «дерево», изображенное на рисунке 1.

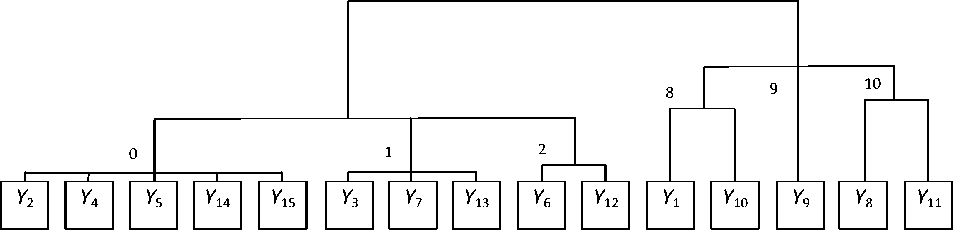
Рис. 1. Итог кластеризации

Таким образом, все респонденты поделились на две группы.

Так же можно было бы воспользоваться другим распространенным методом – методом k -средних. В отличие от древовидной классификации, метод k -средних разбивает всю выборку по заданным признакам на указанное количество кластеров. Таким образом, чтобы использовать этот метод, нужно знать или предполагать, сколько кластеров мы хотим иметь [2].

Следующий этап методики – обработка ответов второй группы вопросов анкеты.

Ответы на вопросы второй группы даются в виде денежных оценок. Указывается максимальная и минимальная сумма по каждому моменту времени в настоящем и будущем, либо при выполнении некоторого условия.

Математическая обработка данных, получен- ных в ходе ответов экспертов на вопросы второй группы, дает информацию о возможном факте наличия корреляции между стоимостью конфиденциальных сведений и потенциальным ущербом от их утраты, хищения, искажения, либо модификации.

Вопросы рассматриваемой группы для некоторой категории конфиденциальных сведений – это парные денежные оценки максимальной и минимальной стоимости информации и величины максимального и минимального ущерба от ее утраты (либо повреждения) на определенный момент времени в настоящем или будущем, либо при выполнении некоторого условия. Предполагается, что на вопросы ответили n экспертов.

Сначала вычислим средние минимальные и максимальные значения стоимости ( X ) и ущерба ( Z ) по каждому вопросу:

n

/ / Aa min, n И n

/у kma max, nk =1

n z . = 1 Yz, min             kmin nk =1

n max           kmax n a=1

Знание этих величин позволяет оценить количественно стоимость информации, а также возможную величину ущерба как по категориям,

так и в совокупности.

Обозначим X_k среднее значение между максимальной и минимальной денежной оценкой k -го эксперта стоимости конфиденциальных сведений в определенный момент времени

X a =

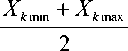
и Z_k – среднее значение между максимальной и минимальной денежной оценкой k -го эксперта ущерба от утраты (либо повреждения) конфиденциальных сведений в тот же момент времени

и проверены гипотезы о значимости выборочной средней.

Таким образом, могут быть исключены из дальнейшего рассмотрения (полностью или частично) конфиденциальные сведения, стоимости которых (или возможные ущербы от утери которых) незначительны.

Возможна связь между стоимостью конфиденциальной информации и величиной ущерба от ее утраты. Для выяснения этого определяем оценку ковариации для X_k и Z_k . Суммируем по k от 1 до n произведения центрированных оценок X_k и Z_k и делим на ( n – 1):

1 ⁿ

P =--- ?/ x a z a .           ⁽²⁰⁾

n - 1 a = 1

Делением полученной оценки ковариации на

среднеквадратичные отклонения получаем оцен-

ку значения коэффициента корреляции р для X_a

и Z : k

ц р = —

Z k

^Z k min ^{+ Z} k max

2 ^,

T x ^ z

индекс k меняется от 1 до n .

Аналогично предыдущей процедуре обработки ответов Y_k , находим для X_k и Z_k оценки математических ожиданий и центрированные оценки:

nn

X = - / X a ,    Z = - / Z a ;   (14)

n И        Пи xk = Xk - X,   zk = Zk - Z.     (15)

kk   kk

Необходимо оценить значимость коэффициента корреляции р ). Для этого используем T- критерий. Вычислим контрольный параметр T по формуле:                ₂

ˆ

T = tc_X 1-^- .           (22)

V n - 2

Вычисляем оценки дисперсии для X_k и Z_k : находим произведения сумм по k от 1 до n квадратов центрированных оценок X_k и Z_k и делим на ( n – 1):

n d=—£x2, xk n -1 a=1

n

D z = Л / z a ². n - - a = 1

Находим несмещенные оценки среднеквадратичных отклонений:

Если оценка коэффициента корреляции, взятая по модулю, меньше, чем вычисленный контрольный параметр |/?| <  T , то корреляция отсутствует. Если больше |/?| >  T , то корреляция есть. Здесь:

t_c = t ( а , n - 2).               (23)

Таким образом, можно сделать вывод о связи стоимости конфиденциальной информации и ущербе при ее утрате. Если коэффициент корреляции значим, то такая связь имеется.

Пример. Предполагается, что на вопросы ответили 15 экспертов (таблица 4).

Вычисляем средние минимальные и максимальные значения стоимости и ущерба:

t x = V D , t z = _x d .       (17)

Как и в случае первой группы вопросов, для каждого математического ожидания могут быть

X min (1) = 41,2; X min (2) = 40,933; X m_m(3) = 42,6;

X max (1) = 144,067; X max (2) = 116,667; X max (1) = 144,067;

построены доверительные интервалы:

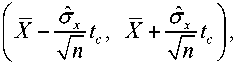
ˆˆ

Z - ^tc, Z + ^tt nn

рассчитаны контрольные параметры H :

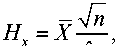
T _x

H_z = Z — z

^T z

Z min (1) = 53,867; Z mJ2) = 34,667; Z m_m(3) = 59,6;

Z max (1) = 127,067; Z max (2) = 109,667; Z max (3) = 133,467.

Находим для X_k и Z_k оценки математических ожиданий:

X (1) = 75,833; X (2) = 78,8; X (3) = 78,733;

Z (1) = 90,467; Z (2) = 72,167; Z (3) = 96,533

и центрированную оценку (таблица 5).

Таблица 4

Номер эксперта	Оценка (в тыс. руб.) возможной стоимости информации (минимальной и максимальной)						Оценка (в тыс. руб.) возможной суммы ущерба (минимальной и максимальной)
	в настоящее время (1)		через 3 года (2)		в случае реализации (3)		в настоящее время (1)		через 3 года (2)		в случае реализации (3)
	min	max	min	max	min	max	min	max	min	max	min	max
1	30	128	30	132	42	93	43	141	23	125	59	110
2	34	80	59	128	34	96	47	93	52	121	51	113
3	40	92	37	92	47	104	53	105	30	85	64	121
4	53	121	43	97	43	135	66	134	36	90	60	152
5	49	97	53	108	42	97	62	110	46	101	59	114
6	33	83	27	85	25	119	46	96	20	78	42	136
7	48	96	50	123	37	108	61	109	43	116	54	125
8	47	148	43	138	47	115	60	161	36	131	64	132
9	47	139	32	100	35	102	60	152	25	93	52	119
10	40	135	24	122	53	149	53	148	17	115	70	166
11	37	111	28	89	50	80	50	124	21	82	67	97
12	33	142	50	145	35	107	46	155	43	138	52	124
13	31	98	59	120	52	146	44	111	52	113	69	163
14	45	136	55	148	46	126	53	149	48	141	63	143
15	51	105	24	123	51	146	64	118	28	116	68	187

Таблица 5

Номер эксперта	Оценка (в тыс. руб.) возможной стоимости информации (минимальной и максимальной)			Оценка (в тыс. руб.) возможной суммы ущерба
	в настоящее время (1)	через 3 года (2)	в случае реализации (3)	в настоящее время (1)	через 3 года (2)	в случае реализации (3)
1	3,167	2,2	–11,233	1,533	1,833	–12,033
2	–18,833	14,7	–13,733	–20,467	14,333	–14,533
3	–9,833	–14,3	–3,233	–11,467	–14,667	–4,033
4	11,167	–8,8	10,267	9,533	–9,167	9,467
5	–2,833	1,7	–9,233	–4,467	1,333	–10,033
6	–17,833	–22,8	–6,733	–19,467	–23,167	–7,533
7	–3,833	7,7	–6,233	–5,467	7,333	–7,033
8	21,667	11,7	2,267	20,033	11,333	1,467
9	17,167	–12,8	–10,233	15,533	–13,167	–11,033
10	11,667	–5,8	22,267	10,033	–6,167	21,467
11	–1,833	–20,3	–13,733	–3,467	–20,667	–14,533
12	11,667	18,7	–7,733	10,033	18,333	–8,533
13	–11,333	10,7	20,267	–12,967	10,333	19,467
14	14,667	22,7	7,267	10,533	22,333	6,467
15	–24,833	–5,3	19,767	0,533	–0,167	30,967

Вычисляем несмещенные оценки среднеква дратичных отклонений Хк и Z::                    |X - £^tc, X + Оц| = (-12,375; 169,842), ax(1) = 209,06, ax(2) = 202,779, ax(3) = 164,888,     ^ nn nn ^(3)

az (1) = 157,695, az (2) = 200,631, az (3) = 208,374.         | Z - ^c , Z + ^c I = ( 3,333; 177,6 ) ,

Строим доверительные интервалы:              ^ ^{nn nn} ^ ⁽¹⁾

^f X - O^t c , X + ^a_. ) = ( - 39,682; 191,348 ) ,      | Z - °M , Z + °M | = ( - 38,691; 183,024 ) ,

I     V n         V n J₀₎^{v                  7}       <     nn         nn J (2)

Рассчитываем контрольные параметры H :

H x (1) = 20,313, H x (2) = 21,432, H x (3) = 23,747,

H z (1) = 27,901, H z (2) = 19,733, H z (3) = 25,9.

Поскольку все контрольные параметры больше t_c = 2,14, то делаем вывод, что мы не можем исключить из дальнейшего рассмотрения ни один вид конфиденциальных сведений, так как их стоимости (или возможные ущербы от утери) являются существенными.

Ищем оценки значений коэффициентов корреляции p для X_k и Z_k :

>5 (1) = 0,873,   /5(2) = 0,995, p (3) = 0,981.

Вычисляем контрольные параметры T :

T (1) = 0,289, T (2) = 0,059, T (3) = 0,115.

Поскольку | p | >  T , то можно сделать вывод о связи стоимости конфиденциальной информации и ущербе при ее утрате. Коэффициент корреляции значим, следовательно, связь имеется.

Следующим этапом исследования является анализ оценок в динамике. Линейная форма связи между случайными переменными (линейная регрессия) занимает особое место в теории корреляции – многие практические задачи хорошо описываются линейной моделью.

Итак, если корреляционная связь между признаками установлена, то, в общем виде, регрессионная модель может быть представлена в виде

У = ф ( x ) + е, (24)

где возмущение ε – случайная переменная, характеризующая отклонение от модельной функции регрессии (расхождения между эмпирическими и теоретическими значениями признака Y). При учете возмущения любой индивидуальный признак Y имеет возможность не попасть на линию регрессии. Основными причинами наличия воз- мущения, как правило, являются следующие:

• •    на вариабельность признака Y влияют помимо признака X и другие факторы;

• •    рассматриваемая экономическая система помимо общего влияния всех имеющих отношение к данному явлению факторов испытывает воздействие основного и непредсказуемого элемента случайности;

• •    значения переменной Y могут содержать ошибки измерения.

Линейный регрессионный анализ рассматривает функцию φ(x), линейную относительно оце- ниваемых параметров, а не относительно переменной X, например следующие зависимости линейны относительно параметров a, :

M(YY ) = a + a x ; M(Y ) = a + a -; x 01 x 01 x

M x ( Y ) = a ₀ + a 1 x + a ₂ x ².

Если для оценки параметров модельной функции регрессии из двумерной генеральной совокупности взята выборка объема n , то регрессионная модель имеет следующий вид:

_ У, = Ф ⁽ x ) ^{+ E} - , (26) где ( x i , y i )( i = 1, n ) - результат i -го наблюдения.

Введя в модель возмущение (слагаемое, характеризующее случайную ошибку) ε_i , определим характеристики распределения вероятностей этой величины. [3]

Простейшая модель регрессионного анализа линейна и по параметрам, и по переменным xi, то есть имеет вид yi = a0 + a1 xi + Ei.             (27)

С помощью параметров a0 и a1 учитывается влияние на зависимую переменную Y объясняющей (предсказывающей) переменной X. Воздействие неучтенных факторов и случайных ошибок наблюдений определяется с помощью остаточной дисперсии op.. Итак, в уравнении (27) величины a0, a1, е неизвестны, причем величину возмущения будет трудно исследовать, поскольку она меняется от наблюдения к наблюдению. Но a0 и a1 остаются постоянными, и, даже не умея находить их значения точно без изучения всех возможных сочетаний Y и X, можно использовать информацию имеющейся выборки для получения оценок а0, а 1 параметров a0 и a1. Оценкой линейной модели (27) по выборке является уравнение регрессии:

Ух = a 0 + а1x или Ух — У = rxy

•—( x - x ).

^c x

от y

Аналогично, линейное приближение xy дается формулой линейной регрессии xy = b0 + b1 У или xy - x = rxy • ^^ (У - У).

^С У

Параметры a ₀, a ₁, b ₀, b ₁ определяются на основе метода наименьших квадратов (МНК). Так как это основная процедура оценивания регрессионных характеристик, остановимся на ней подробнее.

Аналитическая процедура МНК заключается в следующем: рассмотрим уравнение регрессии yi = a0 + a1 x, + Ei (i = 1,n).(30)

Сумма квадратов отклонений от «истинной» линии равна nn

S=E E =E(y-- a,- a1 x-)2.(31)

l=1

Подберем значения оценок a0 и a1 так, чтобы их подстановка вместо a0 и a1 в уравнение регрессии давала наименьшее возможное (минимальное) значение функции S. Для это- го находим ее частные производные по пара- метрам:

д S д а ₀ д S да 1

n

= - 2 E ( У - l = 1

n

=-2E x-( yi i =1

a ₀ - a 1 x_-)

^- a ^- a x ),

минимальное значение получим при подстановке оценок ( a 0 , a 1 ) вместо ( a ₀, a 1 ) и приравнивая выражения частных производных к нулю, т.е.

n

E ⁽ У • ^- a 0 - a l x) = ⁰

¹=¹                                        (33)

E x⁽ y* ^- a о - a i x) = ^0.

- i = 1

После перегруппировки и приведения подоб- ных получим систему нормальных уравнений:

nn a о n+ai e х=E y -l=1            -=1

nnn a о E x + ai E x2 =E xy.

i = 1                    - '= 1                - "= 1

Решив эту систему уравнений любым известным способом, получим значение оценок коэффициентов регрессии. Можно выразить оценки ( a ₀, a ₁) явным образом. Решение системы нормальных уравнений относительно угла наклона прямой дает уравнение

E зд-[ ( Е x i )( E у ) ], n

E x . ^! -( E x )¹/ n

E ^{( x} - ^{- x )(} y - ^- y )

E ( x - x )²   .

Решение системы нормальных уравнений относительно свободного члена дает такой резуль- тат:

a о = У - a 1 x .                 (36)

Итак, предсказывающее (подобранное) уравнение регрессии yx = a 0 + a1x.                (37)

Подставив в него полученное выражение для свободного члена a ₀, получим оцениваемое уравнение регрессии:

y x = y + a 1 ( x - x ).           (38)

Из последнего уравнения видно, что если положить x = x , то y_x = y , т.е. точка ( x , y ) лежит на подобранной линии регрессии.

Коэффициент регрессии a ₁( b ₁), характеризующий линейную связь, позволяет рассчитать, на сколько в среднем изменится признак при изменении на единицу меры другого, связанного с ним, признака .

По уравнению регрессии можно составить таблицу предсказанных значений yx для каж- дого значения x из выборки, а значит, найти остатки yi - yx - разности между тем, что наблюдалось, и тем, что предсказывается с помощью регрессионного уравнения.

В теории математической статистики выведена формула выборочной оценки s_e ² остаточной дисперсии с^ ; определены формулы нахождения доверительного интервала для прогнозов значений (определения неизвестных возможных значений) зависимой переменной по уравнению регрессии; дан метод оценки уравнения регрессии – возможность установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной (дисперсионный анализ) [3].

На практике для проверки согласия построенной линии регрессии с результатами эксперимента можно воспользоваться идеей любой регрессии: часть изменений измеряемой величины Y связать с изменением внешних переменных (в двумерном случае – с X). Предполагая, что Y не зависит от X , за меру разброса результатов эксперимента принимаем сумму квадратов отклонений от среднего арифметического, т.е. величину nn e1 =E(y- -y)2, где y = -Ey-.       (39)

= 1                               n = 1

Далее предполагаем линейную зависимость между признаками, то есть считаем, что построена регрессия yx = a0 + a1 x. Теперь за меру разброса принимаем сумму квадратов отклонений от линии регрессии: n e2 =E[ y-- (a 0+a1x-)]2.            (40)

= 1

Если e 1 ® e ₂, то аппроксимирующая функция выбрана неудачно и подходящую линию регрессии стоит искать не среди прямых, а среди парабол, гипербол и т.п., то есть кривых другого вида [4].

Пример . Предположим, что зависимость между стоимостью информации и возможным ущербом (оценивается ситуация в настоящее время) описываются уравнением (35).

Найдем сумму квадратов отклонений от «истинной» линии:

E ^{( x} - ^{- x )(} у- ^- y )

a1(1) =          42— = 0,758.

E(x-- x)

Решение системы нормальных уравнений относительно свободного члена дает такой результат:

a ₀ = y - a 1 x = 32,956.

Тогда предсказывающее (подобранное) уравнение регрессии:

y_x = 32,956 + 0,758 x .

Проверим согласие построенной линии регрессии с результатами эксперимента. За меру разброса результатов эксперимента принимаем сумму квадратов отклонений от среднего арифметического: n ei = L (У-- У )2 = 157,695.

i = 1

Далее предполагаем линейную зависимость между признаками, то есть считаем, что построена регрессия y x = a 0 + a 1 x . Теперь за меру разброса принимаем сумму квадратов отклонений от линии регрессии:

e 2 = L [ У , — ( a 0 + a 1 X )] 2 = 524,372. i = i

Поскольку e 1 <  e 2 , то делаем вывод, что аппроксимирующая функция выбрана верно.

Построим тренд по данному уравнению (рис. 2).

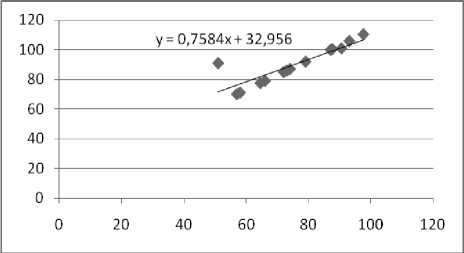
Рис. 2

С помощью найденного уравнения регрессии мы можем сделать прогноз возможного ущерба при заданной стоимости информации в данных условиях безопасности.

Следующим этапом исследования является анализ оценок средств защиты, который проводится на основе ответов экспертов на вопросы первой и второй групп.

Поскольку возможно множество вариантов, то в целях структуризации определим контрольные точки для первой группы вопросов – это 4 и 7. Тогда процесс обработки вопросов и формулировки выводов будет выполнен по следующему алгоритму.

Находим по формуле (1) оценку математи ч еских ожиданий ответов экспертов на вопрос ( Y ) .

• 1.    Если Y <  4, находим математическое ожидание ответов экспертов на вопросы второй группы. Если оценка математического ожидания оценки величины ущерба меньше оценки математического ожидания стоимости информации более чем в 1,5 раза, то предлагаем службе безопасности уменьшить затраты на четверть на политику безопасности по данному критерию и провести опрос заново. Если же математическое

• 2.    Если 4 <  Y <  7, находим оценки математического ожидания ответов экспертов на вопросы второй группы, и здесь возможно несколько случаев:

ожидание оценки величины ущерба больше или равно оценке математического ожидания стоимости информации либо меньше менее чем в 1,5 раза, то советуем службе безопасности оставить политику неизменной, но через некоторое время провести повто р ное исследование.

• a)    оценка математического ожидания оценки величины ущерба меньше оценки математического ожидания стоимости информации более чем в 1,5 раза. Результатом исследования будет совет службе безопасности оставить политику неизменной, но через некоторое время провести повторное исследование;

• b)    оценка математического ожидания оценки величины ущерба равна оценке математического ожидания стоимости информации, в этом случае предлагаем службе безопасности оставить политику неизменной;

• c)    если же оценка математического ожидания оценки величины ущерба больше стоимости информации, то советуем ужесточить политику безопасности .

• 3.    Если Y >  7, находим оценки математического ожидания ответов экспертов на вопросы второй группы и тогда, вне зависимости от размеров величины ущерба и стоимости безопасности, необходимо ужесточить меры по обеспечению информационной безопасности.

Таким образом, описанная нами методика позволяет оценить риск потери конфиденциальной информации, а также помогает определить меры для снижения вероятности ее потери.