Методика оценки точности формирования сигналоподобных помех бортовым радиолокационным станциям
Автор: Антипенский Р.В., Козирацкий Ю.Л.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 4 т.10, 2017 года.
Бесплатный доступ
Рассмотрена методика и получена оценка точности формирования сигналоподобных помех бортовым радиолокационным станциям разведки для различных значений коэффициентов амплитудной неравномерности амплитудно-частотной характеристики детектора модулирующей функции сигналов и разрядности АЦП цифрового формирователя сигналоподобной помехи.
Сигналоподобная помеха, оценка точности формирования, амплитудная неравномерность
Короткий адрес: https://sciup.org/146115892
IDR: 146115892 | УДК: 621.398 | DOI: 10.17516/1999-494X-2017-10-4-475-483
Текст научной статьи Методика оценки точности формирования сигналоподобных помех бортовым радиолокационным станциям
В настоящее время при разработке техники РЭБ с бортовыми радиолокационными станциями противника (БРЛС) все большее внимание уделяется интеллектуальным способам радиоподавления, основанным на создании сигналоподобных помех. При этом основными процедурами создания таких помех являются измерение параметров зондирующих сигналов, детектирование модулирующих функций сигналов и воспроизведение сигналоподобных помех на основе произведенной оценки с наименьшими отклонениями. Неточность конструктивного воспроизведения алгоритмических характеристик приемных и формирующих устройств приводит к существенным ошибкам, которые значительно увеличиваются, когда в принимаемой смеси содержатся помеховые воздействия. Задачи измерения параметров и воспроизведения радиосигналов решаются как аналоговыми, так и цифровыми методами. При аналоговой обработке и формировании радиосигналов на точность воспроизведения влияют в основном отклонения рабочих характеристик устройств от теоретически рассчитанных [1, 2]. При цифровой обработке и формировании радиосигналов основную погрешность, как известно, вносят аналого-цифровые преобразователи (АЦП).
Целью исследования является разработка методики оценки точности формирования сигналоподобных помех бортовым РЛС-методом имитационного моделирования по информационному показателю подобия [3].
Разработка методики и модели для оценки точности формирования сигналоподобных помех
В современных бортовых РЛС широко используются сигналы с нелинейной частотной модуляцией (НЛЧМ), база которых B = Δf ∙ Ts может достигать значений, близких к 1000 [3]. Методы и алгоритмы измерения временных и частотных параметров таких сигналов достаточ-– 476 – но полно изложены в работах [4, 5] и реализованы в современной аппаратуре радиотехнической разведки. Однако вопросы выявления (детектирования) модулирующей функции НЛЧМ-сигналов, играющих ключевую роль при формировании сигналоподобных помех, остаются не освещенными, поэтому определение закона и параметров модулирующей функции (МФ) таких сигналов, очевидно, представляется наиболее важными.
Для определения модулирующей функции НЛЧМ-сигналов обычно используются детекторы сигналов с частотной модуляцией, представляющие собой цепь с линейно возрастающей (убывающей) амплитудно-частотной характеристикой (АЧХ) на участке, соответствующем спектру детектируемого сигнала. При этом в современной радиоэлектронной аппаратуре для получения линейной детекторной характеристики с большой крутизной на относительно широком участке частот используются детекторы, построенные каскадным соединением нескольких звеньев. В случае отклонения реальных характеристик таких детекторов от оптимальных линейность АЧХ нарушается, возникает неравномерность как по уровню, так и по частоте (количеству волн). Для исследования влияния неравномерности АЧХ детектора на точность определения модулирующей функции НЛЧМ-сигналов введем коэффициенты относительной амплитудной К А и волновой неравномерности К В АЧХ детектора:
MAX ( 2 n fn + ka • sin(2 n f • ks ) ) - MIN ( 2 n fn + ka • sin(2 n f • ks ) ) MAX ( 2 n fn + ka • sin(2 n f • ks ) )
К В
где 2π f n , 2π f v – нижняя и верхняя граничные частоты линейно возрастающего участка АЧХ детектора; kа – амплитуда неравномерности АЧХ; ks – частота флуктуаций (количество волн) АЧХ детектора. Тогда модель комплексной передаточной функции (КПФ) детектора НЛЧМ-сигнала с учетом необходимости управления коэффициентами амплитудной и волновой неравномерности может быть следующего вида:
h DM ( f ) = f [ fn < f < fv , ( j W + ka • sin(2 n f • ks ) ), 0 ] ,
где if – условная функция вида (условие, оператор 1 при выполнении условия, оператор 2 при невыполнении условия). НЛЧМ-сигнал с гармоническим законом изменения модулирующей функции может быть представлен таким образом:
t
S nlcm ( t ) = U s.n J (2 n f 0 + в + m A sin^t )) dt
A
V o
где U 0 – амплитуда сигнала; f 0 – несущая частота; β = 2πΔ f / T s – скорость изменения частоты внутри импульса; Af - девиация частоты; m4, mB - амплитудный и волновой параметры гармонического закона изменения частоты НЛЧМ-сигнала [2]. Раскрыв интеграл в правой части формулы (4), можно получить выражение для НЛЧМ сигнала с гармоническим законом изменения модулирующей функции:
/
S nlcm ( t ) = U o Sin 2 n f , t +
pt 2 mA л zo A J
—- + ^A- (1 - cos(2 n mBt )) I .
V
2 2 n mB
Используя спектральный метод анализа преобразований сигналов в цепях, можно найти модулирующую функцию НЛЧМ-сигнала. Для этого выполним прямое преобразование Фурье (процедура CFFT(x) ), перемножение комплексного спектра сигнала с КПФ детектора и обратное преобразование Фурье во временную область (процедура ICFFT(x) ) [6]. Выделив реальную часть получившегося массива отсчетов, имеем временное представление искомой модулирующей функции, в котором изменение частоты НЛЧМ-сигнала соответствует изменению амплитуды модулирующей функции:
S mf ( t ) = Re ICFFT h dm ( f ) • CFFT [ S _ ( t ) ] .
После определения закона модулирующей функции НЛЧМ зондирующего сигнала в приемном устройстве станции сигналоподобных помех выполняется преобразование выявленной функции в цифровую форму с помощью АЦП для последующей записи в оперативную память и цифрового синтеза помехи. На точность воспроизведения синтезированной сигналоподобной помехи по запомненной модулирующей функции будут влиять возникшие при аналогоцифровом преобразовании шумы квантования и шумы ограничения. При условии близости закона модулирующей функции к линейному на протяжении длительности одного зондирующего импульса шумом ограничения в АЦП можно пренебречь. Тогда выражение для сигналоподобной помехи, сформированной на основе детектированной модулирующей функции, можно представить в следующем виде:
S sp ( t ) = U o Sin
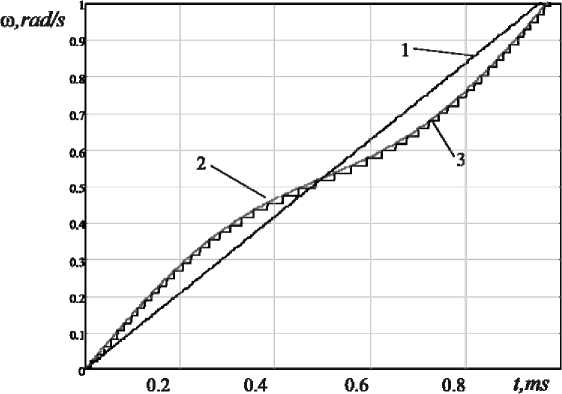
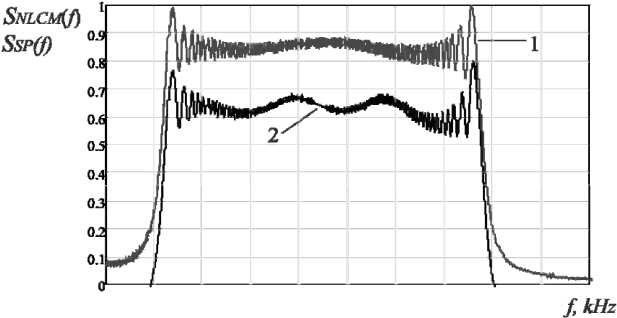
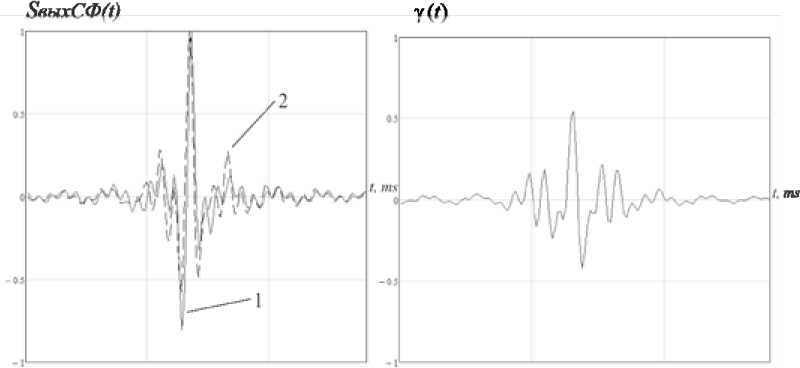
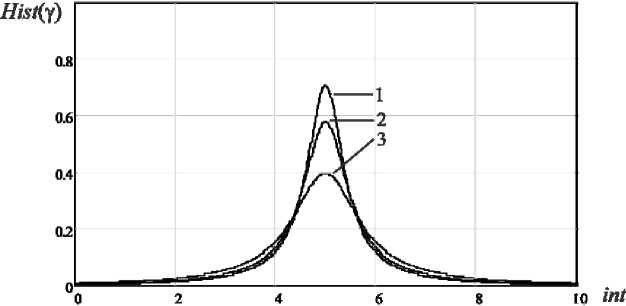
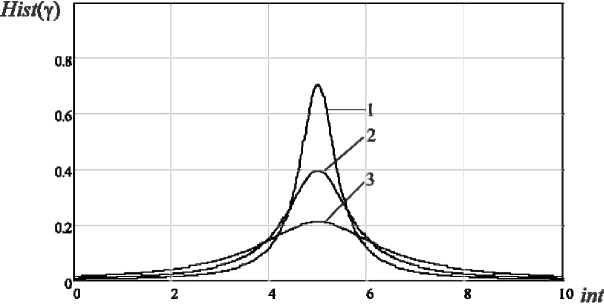
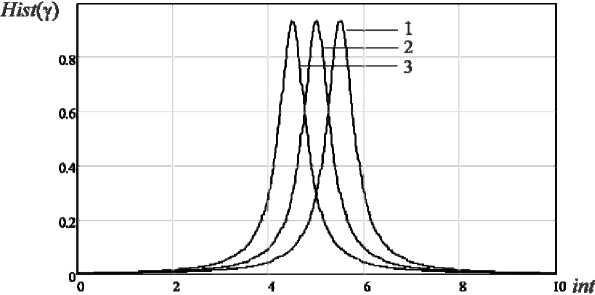
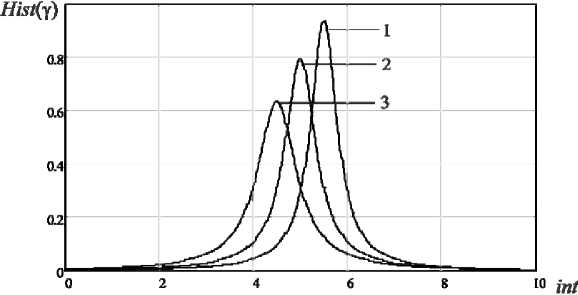
. ((2 ADC 2 2p максимальная и минимальная круговые частоты (амплитудные значения при оцифровке) модулирующей функции; р – разрядность АЦП, определяющая количество квантуемых уровней модулирующей функции. В качестве информационного показателя подобия помехи и сигнала БРЛС воспользуемся функцией разности сигналов на выходе согласованного фильтра (СФ) для НЛЧМ-сигнала и сигналоподобной помехи: Y(. t) = SSF NLCM(t ) SSF SP(t ) . Идеальным согласованным фильтром для НЛЧМ сигнала является, как известно, комплексно-сопряженная со спектром сигнала функция. Тогда искомые функции выхода согласованного фильтра для НЛЧМ-сигнала и сигналоподобной помехи можно будет найти, перемножив их комплексные спектры с комплексно-сопряженным спектром НЛЧМ-сигнала и выполнив обратное преобразование Фурье. Схема имитационной модели для оценки точности формирования сигналоподобных помех бортовым РЛС представлена на рис. 1. Рис. 1. Схема имитационной модели для оценки точности формирования сигналоподобных помех бортовым РЛС Рис. 2. Нормированные модулирующие функции сигналов с ЛЧМ (1) (для сравнения), гармонического НЛЧМ (2) и детектированного НЛЧМ после квантования (3) На рис. 2 изображены нормированные модулирующие функции сигналов с ЛЧМ (1) (для сравнения), гармонического НЛЧМ (2) и детектированного НЛЧМ после квантования (3) с раз-– 479 – Рис. 3. Нормированные амплитудные спектры НЛЧМ сигнала (1) и сигналоподобной помехи (2), воспроизведенной с неравномерностью амплитудно-частотной характеристики детектора КА=0.2, КВ=2 а б Рис. 4. а – сигналы на выходе СФ НЛЧМ (1) и сигналоподобной помехи (2); b – функция оценки в нормированном виде для базы В=300 зондирующего сигнала БРЛС рядностью АЦП р=6 (число квантуемых уровней модулирующей функции при этом составит 26=64) с параметрами: длительность импульса 1 мс, mA=30 (для повышения наглядности графика), mB=1. На рис. 3 показаны нормированные амплитудные спектры НЛЧМ-сигнала (1) и сигналоподобной помехи (2), воспроизведенной с неравномерностью частотной характеристики детектора МФ КА=0.2, КВ=2. Спектр сигналоподобной помехи показан смещенным по уровню на 0.2 - отчетливо виден вклад ошибок детектирования в форму спектра. Моделирование выполнялось на про -межуточной частоте 200 кГц. На рис. 4а показаны сигналы на выходе СФ НЛЧМ (1) и сигналоподобной помехи (2), на рис. 4б – функция оценки для базы В=300 зондирующего сигнала БРЛС. Исследование оценки точности формирования сигналоподобной помехи На рис. 5 показаны нормированные огибающие гистограмм распределений оценки (Hist(Y)) для следующих параметров модели: база сигнала В=100, разрядность АЦП р=5(3),6(2),7(1), коэффициент амплитудной неравномерности АЧХ детектора МФ КА=0,05, на рис. 6 – база сигнала В=100, разрядность АЦП р=5, коэффициенты амплитудной неравномерности АЧХ детектора МФ КА=0,05(1); 0,1(2); 0,2(3). По оси абсцисс отложены номера интервалов int, в которых распределена функция оценки γ(t). Границы интервалов вычислялись по формуле max[/( t)]- min[/( t)] int k = min[/( t)]+ n • k, (9) где N - число интервалов; k - порядковый номер интервала [6]. Распределение оценки соответствует распределению Коши с различными параметрами расположения и формы с вероятностью 0,985 по критерию Пирсона. Из представленных зависимостей видно, что большую Рис. 5. Нормированные огибающие гистограмм распределений оценки: база сигнала В=100, разрядность АЦП р=5(3),6(2),7(1), коэффициент амплитудной неравномерности АЧХ детектора МФ КА=0,05 Рис. 6. Нормированные огибающие гистограмм распределений оценки: база сигнала В=100, разрядность АЦП р=5, коэффициенты амплитудной неравномерности АЧХ детектора МФ КА=0,05(1); 0,1(2); 0,2(3) Рис. 7. Нормированные огибающие гистограмм распределений оценки: В=500, разрядность АЦП р=5(3),6(2),7(1), коэффициент амплитудной неравномерности АЧХ детектора МФ КА=0,05 Рис. 8. Нормированные огибающие гистограмм распределений оценки: В=500, разрядность АЦП р=5, коэффициенты амплитудной неравномерности АЧХ детектора МФ КА=0,05(1); 0,1(2); 0,2(3) ошибку в оценку точности формирования сигналоподобных помех вносит неидеальность АЧХ детектора модулирующей функции, а не разрядность АЦП синтезатора помехи. Приемлемая точность сигналоподобной помехи для базы зондирующих сигналов БРЛС В=50-150 может быть достигнута при разрядности АЦП не менее 5 и коэффициенте амплитудной неравномерности АЧХ детектора МФ, не превышающем значения КА=0,1. На рис. 7 показаны нормированные огибающие гистограмм распределений оценки для сигнала с базой В=500, разрядность АЦП р=5(3),6(2),7(1), коэффициент амплитудной неравномерности АЧХ детектора МФ КА=0,05, на рис. 8 – для сигнала с базой В=500, разрядность АЦП р=5, коэффициенты амплитудной неравномерности АЧХ детектора МФ КА=0,05(1); 0,1(2); 0,2(3). Характер распределения оценки остается таким же, наблюдается изменение параметра расположения. С увеличением базы сигнала требования к точности формирования помехи снижаются – очевидно, что сказывается выигрыш от большего сжатия сигнала в согласованном фильтре. По-прежнему неидеальность АЧХ детектора модулирующей функции вносит большую ошибку в оценку точности, однако коэффициент амплитудной неравномерности АЧХ де-– 482 – тектора может достигать значения КА=0,2, точность формирования сигналоподобной помехи остается при этом на приемлемом уровне. Заключение Таким образом, разработана методика и получена оценка точности формирования сигналоподобных помех НЛЧМ-сигналам бортовых РЛС для различных значений коэффициентов амплитудной неравномерности АЧХ детектора модулирующей функции сигналов и разрядности АЦП цифрового формирователя сигналоподобной помехи. Установлено, что приемлемая точность сигналоподобной помехи для базы зондирующих сигналов БРЛС В=50-150 может быть достигнута при разрядности АЦП не менее 5 и коэффициенте амплитудной неравномерности АЧХ детектора, не превышающем значения КА=0,1. С увеличением базы сигнала требования к точности формирования помехи снижаются – коэффициент амплитудной неравномерности АЧХ детектора МФ может достигать значения КА=0,2 при разрядности АЦП р=7.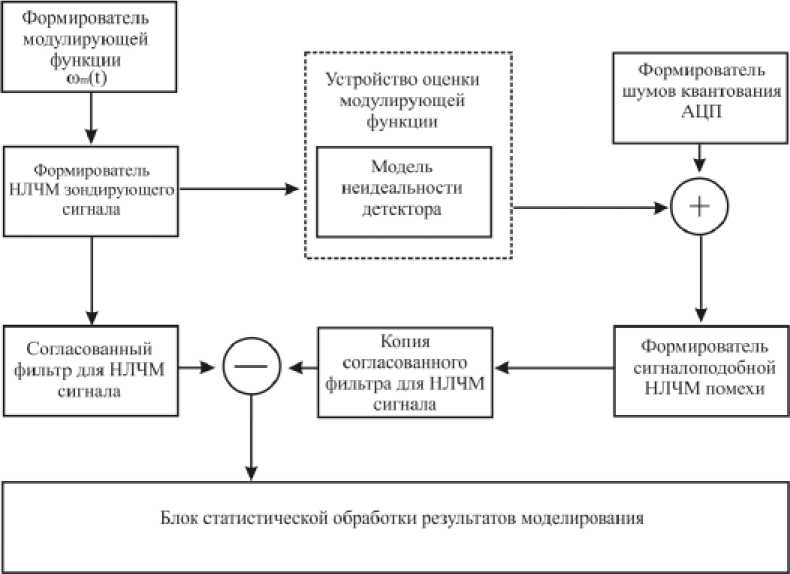
Список литературы Методика оценки точности формирования сигналоподобных помех бортовым радиолокационным станциям
- Антипенский Р.В., Козирацкий Ю.Л. Оценка ошибки детектирования частотно-модулированных сигналов в присутствии помех. Радиотехника, 2008, 22, 19-24
- Антипенский Р.В., Козирацкий Ю.Л. Оценка точности воспроизведения сигналов с линейной частотной модуляцией. Радиотехника, 2009, 23, 15-19
- Добыкин В.Д., Куприянов А.И. и др. Радиоэлектронная борьба. Цифровое запоминание и воспроизведение радиосигналов и электромагнитных волн. М.: Вузовская книга, 2009. 360 с
- Смирнов Ю.А. Радиотехническая разведка. М.: Воениздат, 2001. 456 c
- Лосев В.В., Бродская Е.Б., Коржик В.И. Поиск и детектирование сложных дискретных сигналов. М.: Радио и связь, 1988. 224 с
- Richard C. Saffe. Random Signals for Engineers using MATLAB and Mathcad. Springer -Verlag, 2000. 376 p


