Методика определения акустических характеристик камер сгорания ракетного двигателя твердого топлива

Проблема акустической неустойчивости горения в ракетных двигателях твердого топлива не менее актуальна по сравнению с жидкостными ракетными двигателями большой тяги [1–4]. Акустическая полость, как правило, имеет сложную геометрическую форму. Зона горения расположена в непосредственной близости к границе раздела фаз – твердый заряд и газовый тракт.

Толщина зоны горения смесевого состава при давлении до 4 МПа и температуре газа порядка (2500–3000) К примерно составляет 70–90 мкм. Тонкая зона горения зачастую оказывается способной усиливать возмущения давления той акустической моды, для которой максимум волны приходится на поверхность горения. Воздействие акустических колебаний давления на процесс горения, в соответствии с критерием Релея, вызывает колебания скорости горения [2–12]. Наличие этой обратной связи приводит к усилению колебания давления в тонкой зоне химических реакций с высокими градиентами температуры, концентрации паров топлива, большими скоростями энерго- и массообмена. В дополнение следует отметить возможный термодинамический нагрев газа при его сжатии. В некоторых случаях важную роль могут играть и колебания акустической скорости. При горении твердых топлив в каналах шашки присутствуют турбулентные пульсации – шумы горения. Они обусловлены различными механизмами возбуждения и имеют различную физическую природу. Звуковой шум обычно связывают с газодинамическими причинами такого же характера, как и в турбулентных газовых потоках. В камерах сгорания регулярные колебания давления с частотой, близкой к собственной (акустической) частоте колебаний газового столба [7–12], могут усиливаться, а чаще стабилизироваться на некотором уровне из-за акустических потерь. Акустическая неустойчивость горения представляет собой автоволновой процесс с обратной связью через воздействие звуковых волн на горение. Параметры волнового процесса: частота, амплитуда и форма колебаний определяются свойствами заряда РДТТ как динамической системы. Звуковой шум в полости камеры также может рассматриваться как автоколебательный процесс [6], в котором источником энергии является тепловыделение при горении, а обратная связь возникает из-за воздействия звуковых волн на горение, при этом возникают незатухающие пульсации стохастического характера [11], имеющие широкую полосу частот и случайные фазы. Однако частотная характеристика акустической полости часто обладает частотной избирательностью, характеризующейся высокой добротностью по отношению к продольной моде [2–4].

В большинстве теоретических работ проводится анализ влияния малых возмущений на устойчивость горения. Однако, учитывая сложный нелинейный механизм процессов преобразования твердого топлива в газовую фазу (прогрев, пиролиз, возгонка и др.), зачастую процесс горения и его взаимодействие с газодинамическими явлениями в акустическом тракте РДТТ характеризуется «жестким» возбуждением автоколебаний. Иначе динамическая система может стать неустойчивой при увеличении амплитуды возмущений выше определенного порогового предела. Возмущения, имеющие амплитуду ниже пороговой, затухают. Жесткое возбуждение колебаний характерно для нелинейных динамических систем. Разработка нелинейных теорий существенно усложняется математическими трудностями. Линейные теории могут быть достаточно полезны для понимания неустойчивости, а в некоторых случаях и для нелинейных приложений.

Оценка устойчивости горения в двигателях твердого топлива может быть выполнена на основе определения баланса акустической энергии в камере сгорания, с учетом притока акустической энергии (вследствие взаимодействия акустических колебаний с процессом горения) и потерь акустической энергии за период колебаний. Диагностическим показателем запаса линейной устойчивости процесса горения является коэффициент (декремент) затухания колебаний [2; 7–12]. Коэффициент затухания имеет определенный физический смысл:

δ ν

E 2 - E 1

2 E _СУМ

где Е 2 – приток акустической энергии, генерируемой колебательной системой за период колебаний; Е 1 – часть энергии, диссипируемой колебательной системой за период колебаний; Е СУМ – акустическая энергия, запасенная системой за период колебаний.

Приток акустической энергии от процесса горения зависит – при определенных фазовых (0 ÷ π/2) cотношениях между колебаниями давления и скорости горения – от амплитуды колебаний давления, увеличиваясь пропорционально квадрату последней. Для определения притока акустической энергии в камерах с горением разработаны экспериментальные методы с использованием Т-образной камеры [3–4]. Потери акустической энергии в газовом объеме камеры сгорания имеют существенное значение при наличии в продуктах сгорания конденсированных частиц. Расчет потерь на границах камеры сгорания, имеющей сложную конфигурацию в случае двигателей твердого топлива, связан с большими трудностями. Эти потери приближенно могут быть определены при проведении экспериментов на моделях камер сгорания без течения газа. Из изложенного следует, что акустические свойства камеры сгорания: частота собственных колебаний, распределение амплитуды колебаний – могут усиливать колебания или их демпфировать, и тем самым влиять на устойчивость горения в двигателе. Необходимо отметить, что свойство камеры сгорания РДТТ как колебательной системы имеют различия со свойствами систем, рассматриваемых в акустике. Отличия связаны с тем, что в камерах сгорания на колебания накладывается высокоскоростной поток газа, влияет специфическая конфигурация сопла, имеются распределенности параметров рабочего процесса и др. Но несмотря на эти важные различия, формы и частоты собственных колебаний существенно не изменяются [2; 7–12], что дает возможность проводить расчеты и эксперименты по определению свойств камеры сгорания как колебательный системы в акустическом приближении, т. е. без учета осложняющих факторов.

В результате теоретических и экспериментальных исследований акустической неустойчивости горения в настоящие время достигнут определенный уровень знаний физических процессов, дающий возможность прогнозировать влияние изменений конструктивных и режимных факторов на области неустойчивости. В РДТТ характерны акустические колебания продольной моды из-за большого отношения длины заряда к диаметру полости ( L / D ≥ 5) , а поперечные моды встречаются значительно реже.

Собственные частоты колебаний и акустические поля давления в камерах сгорания РДТТ. Акустические волны, распространяющиеся в трактах различных систем, часто имеют длину волны сопоставимую с размерами каналов. В этом случае целесообразно рассмотрение решение волнового уравнения в виде стоячих волн. Стоячие волны образуются в результате взаимодействия прямых и отраженных от «жестких» стенок волн. Рассмотрим суперпозицию двух волн F , движущихся на встречу друг другу с постоянными фазовыми скоростями. Для этого представим решение волнового уравнения в виде суммы частных решений вида [7]

02F(x}      э , х д2FUA      7 7 / X 7 / X k2 F (x);          k 2 c0 F (t W F (t).(2)

д x

2,22

где го = k c ₀ .

Система (2) эквивалентна уравнениям, описывающим упругие колебания материальной точки. Решения этих уравнений представляют гармонические колебания со своим сдвигом фазы:

F (x) = A cos (kx + фx); F(t) = B cos (гоt + фt).(3)

Решение волнового уравнения записывается в виде произведения

V = F (x) F (t ) = C cos (kx + фx) cos (го t + фt).(4)

Здесь C = A B .

Функция F ( x ) описывает распределение амплитуды колебаний, постоянной по времени, а функция F ( t ) показывает, что все точки волны движутся синхронно. Колебание не распространяется, смещения всех точек достигают своих максимальных или минимальных значений в одни и те же моменты времени. Полученное частное решение называют стоячей волной или собственным колебанием. Для описания волнового движения в неограниченном объеме требует бесконечного числа решений с непрерывным спектром частоты ω и k = ω / с 0 . Здесь c 0 – скорость звука, а k – волновое число. Общее решение имеет вид интеграла Фурье. В случае реализации стоячей волны в конечном тракте с жесткими стенками, находят как общее решение, так и каждое частное, удовлетворяющее граничным условиям

4v(x, t ) = 0; 5^1 = 0. dx

Каждое частное решение должно удовлетворять волновому уравнению и описывать возможное колебание системы

Vv (x, t) = Av cos (kVx + Фvx) cos (kvcоt + Фvt),(5)

где ψ ν ( x , t ) – потенциал скорости; ω ν = k ν c 0 – круговая частота колебаний.

Если функция потенциала на границах тракта равна нулю, то для любого момента времени должно выполняться:

Av cos Tvx cos (»v t + Фvt) = Av cos (®v t + Фvt) cos (kvl + Фvx ) = 0,(6)

Фvx =vn, kvl = vn, v = 1, 2, ... .(7)

Каждое частное решение может быть представлено выражением

V v ( x, t ) = Vv (x) cos (^vt + Tvt),(8)

где

( \       ■ vnx , vn c₀

VV (x) = Av sin —, ®v = kvC0 = —|— •

Функция ψ_ν ( x ) описывает собственные колебания системы в отсутствии внешних сил и затухания, а частоты ω ν – собственные круговые частоты.

Более общее решение можно получить, сложив все собственные колебания системы с соответствующими амплитудами:

V v ( x , t ) = Z v v ( x ) cos ( ® v t + T vt ) = Z A v sin ^v7 x cos ( ® v t + T vt ) , v = 1, 2, ... .      (10)

ν l

Рассмотрим частный случай распространения плоской волны в движущемся потоке и найдем соотношения для пульсаций скорости и возмущений давления. Представим общее решения уравнения в виде двух волн, движущихся в противоположном направлении:

v = Ae « t - i^k 1 x + ве _m t - ik ² x ,                                     (ii)

где

k i = ^ю ; ® = k i ( c 0 + v 0 ) ; ^k 2 = ^ю ; ^=- ^k 2 ( ^c 0 ^- v 0 ) •                  ⁽¹²⁾

^c 0 ^{+ v} 0                         ^c 0 ^v 0

Пульсации скорости vx _ -    = ik Ae - k1 x+i to t + ik2 Be " k2 x+i“ t.(13)

d x

Возмущения давления связаны с потенциалом скорости уравнением

„ c2 p' S^S^

⁸ P =   =^T ⁺ v 0 я .

у   Po   dt

Продифференцируем это выражение по времени t и по координате х p' = p0 (itoAe - k1 x+im t + ito Be - k 2 x+im t - v0 ik1 Ae - k1 x+im t - v0 ik2 Be - k2 x+im t).

Далее введем новые коэффициенты, тогда выражение для возмущения давления несколько упростится p f _ ceitot - ik1 x + De- tot - ik2 x

где коэффициенты равны:

C _ ( i to - v _o ik₁ ) p _o A _ ^ZPo c ^{o to c} o ^{+ v} o

A; D = ( ito- v0 ik2 )p0 B =

iPo c oto B

c ₀

v ₀

С учетом вида этих коэффициентов, выражение для возмущения скорости будет выглядеть следующим образом:

f               + 1 to t - ik i x              + 1 to t - ik o x

v x _----- e ¹ e ² .

^P o ^c o              ^P o ^c o

Выразим механическое сопротивление среды в виде отношения возмущений давления к пульсации скорости. Для волны, бегущей по потоку, это отношение равно pr- _Poco, vx+ а против потока

p -

— _-Po co. v-

Величина

z c = P o c 0

является волновым сопротивлением среды. Таким образом, звуковое давление равно скорости распространения плоской волны умноженное на величину волнового сопротивления и имеет положительный знак, если волна распространяется в положительном направлении координатной оси. При распространении волны в противоположном отрицательном направлении скорость частиц отрицательна, а звуковое давление положительно. Волновое сопротивление характеризует среду и является для нее постоянной величиной. Дисперсионное соотношение для возмущения в виде плоской волны энтропии определим так [7–8]:

^{to- k}s^v o

_ o ^ v

to

⁰ k s ,

отсюда

8 5 _ 8 S H e i ⁸ t ^{- ik} s ^x .

Волны энтропии распространяются без дисперсии, а вихревые плоские волны не существуют.

Рассмотрим плоские стоячие волны в закрытой с одной стороны цилиндрической камере сгорания. Примем решение волнового уравнения в виде v = ( A cos kx + B sin kx ) e - i ^to t . Тогда при х = 0

v X =      = (-Ak sin kx + Bk cos kx) el “ t = 0.(18)

^d x x = 0

Тождество (18) выполняется при В = 0, отсюда следует, что возбуждаются стоячие колебания, одинаковые по фазе во всех точках одновременно

V = A cos (kx) emt; ^ = (- Ak sin kx) emt.(19)

При х = l колебательное давление считаем равным нулю (ψ = 0), тогда cos ( kl ) = 0; отсюда получаем kl = m π/2, при этом m – нечетные.

Таким образом, для трубы, закрытой с одного конца и открытой с другого fmn ) 5v mnf w = A cos x e™t; v‘= —= Ak sin    e™t,(20)

( 21 ) x ax    21 ( где m = 1, 3, 5, … .

В случае закрытой с двух сторон трубы, т. е. при х = 0 и х = l , из выражения (20) следует В = 0 и sin ( kl ) = 0, откуда m π = kl ; m = 0, 1, 2, …

V = A cos f m^ x) e1 юt.(21)

( 21 )

Газовая полость камер сгорания двигателей твердого топлива имеет более сложную конфигурацию. На рис. 1 показана газовая полость, которая образуется, если заряд плотно связан с камерой и горение происходит по внутренней поверхности канала заряда и торцам.

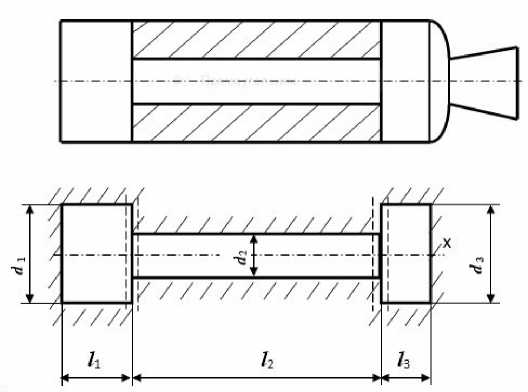
Рис. 1. Схема газовой полости камеры: а – конструктивная; б – расчетная

Fig. 1. Diagram of the gas chamber of the chamber: a – constructive; b – calculated

Распространение колебаний в такой сложной полости сопровождается дифракционными явлениями. Считая, что большая часть звуковой волны, подходящей к соплу, отражается от него в камеру (вследствие наличия сужающейся части сопла и изменения акустического сопротивления среды ρc) для упрощения рассматриваемой колебательной системы заменяем сопло жесткой стенкой. Разбиваем сложную газовую полость на три цилиндрические полости, каждая из которых имеет постоянную площадь поперечного сечения. Для каждой составной части сложной полости представляем решение волнового уравнения. Далее для собственных частот и распределения колебательных давлений и скоростей используем метод «сшивания» акустических полей на границах полостей [13], учитывая непрерывность среды при переходе звуковой волны из одной полости в другую. Например, условия непрерывности среды при переходе из первой полости во вторую определяются равенством звуковых давлений (или потенциалов скорости) при х = l1

* 1 ( / 1 ) = * n ( 1 1 )                                              (22)

и равенством объемных скоростей

S ^    S, № ,                         (23)

у d x J     у d x J 2

где S 1 и S 2 – площади сечения первой и второй полостей.

Решение волнового уравнения для сложной трехступенчатой полости следует записать в виде ряда с учетом того, что в полости имеется стоячая волна и дифракционные отражения колебаний при переходе из полости в полость (при х = l 1 и х = l 2 ), т. е. для каждой полости с учетом нулевых граничных условий для колебательных скоростей при х = 0 и х = l 1 + l 2 + l 3 . Если для упрощения задачи пренебречь дифракцией акустических волн на стыках полостей то, решение уравнения (21) для стоячих волн в каждой полости может быть записано в виде

• *    i = A[ k (x -a i)] eю t,

i – номер полости, α i – параметр, определяющий условия фазового перехода из полости в полость; A i – амплитуда колебаний.

Для первой полости

• * 1 = A1 [ k (x -a1)] ei “ t.(25)

Из нулевого граничного условия для колебательной скорости v = 0 x = 0 следует, что α 1 = 0. Отсюда

• * 1 = A1cos (kx) ei “ t,(26)

а для второй полости

* 2 = A2cos [ k (x-a 2)] ei “ t.(27)

Аналогично и для третьей полости

• * 3 = A3 cos [k (x - a3)] ei“t.(28)

Однако из нулевого граничного условия для колебательной скорости

Sw, v = —3 = 0 при х = 11 + 12 + 13 следует, что a3 = 11 + 12 + 13. dxtk

Определить неизвестные волновое число k и параметр α ₂ можно, если подставить выражения (26) и (27) в условия (22) и (23), характеризующие непрерывность среды при x = l 1 . Исключив из системы уравнeний коэффициенты A 1 и A 2 , получаем взаимосвязь неизвестных параметров

S tg k11 = T2-tg [ k (11 -a2 )].                                    (29)

S ₁

Условия «сшивания» акустических полей при x = l 1 + l 2 выполним аналогично условиям (22) и (23):

^5^)    ^Vl

V2 (li + l2 ) = V3 (li + l2 ); S2 I      I = S3 I      I *

_V d x ) ₂     Vox ) ₃

Исключая амплитудные коэффициенты A 2 и A 3 , получаем второе уравнение для определения неизвестных k и параметра α 2

S

-³tg kl з + tg [ k ( l i + l 2 - а з ) ] = 0.

S ₂

Решая совместно алгебраические уравнения (31) и (33), получаем трансцендентное алгеб-

раическое уравнение

SS tg kl 2 ⁺    tg ^kl i ⁺ — tg kl 3

S ₂ S ₂

- ^ 1^³ tg k ^ • tg kl ₂ • tg kl ₃ = 0.

S ₂ 2  123

В зависимости (32) входят геометрические размеры газовой полости и неизвестное волновое число k .

Распределение амплитуды колебаний давления (в относительных величинах) по длине камеры сгорания можно определить по следующим формулам:

для первой полости:

S P 1         7

8 p 1 = — = cos kx ;

p ₀

для второй полости:

8p 2 =

p ‘ _     cos k1 1

p ₀

где α 2 вычисляется из уравнения (30)

cos [ k (11 -а2)]

cos [ k (x-а2)],

α2

[ S kl i - arctg -1 tg kl i ___________ [ S 2

k

.

Для третьей полости:

p ‘ cos ^kl i • cos [ k ( ^l i + ¹ 2 ^-а 2 ) ]

⁸ p 3 =   = eoskl eosVktl -a     cos ^[ k ⁽ x -^а з ^)] *

p о       cos kl 3 cos [ k ( l i а 2 ) I

Здесь p 0 – амплитуда давления при x = 0.

На рис. 2 представлен график p / p 0 = f ( x ) по расчетным данным.

По описанному алгоритму могут быть получены приближенные расчетные зависимости и для других конфигураций газовой полости камер сгорания. Сравнивая расчетные данные, найденные по приближенным формулам, с экспериментальными данными, полученными на акустической установке, можно выяснить точность расчетов. К задачам экспериментальных работ следует отнести определение собственных резонансов акустической продольной моды и оценку потерь колебательной энергии.

Описание экспериментальной установки

Экспериментальная установка состоит из модельной камеры, электродинамического излучателя, звукового генератора, задающего частоту возбуждения, усилителя и приемно-регистрирующей аппаратуры.

Модельная камера выполнена разъемной и состоящей из нескольких секций. Внутрь камеры могут вставляться макеты заряда. Геометрические размеры акустической полости представлены на рис. 2.

В качестве источника малых колебаний применяются звуковые головки типа 10 ГРАД-5. Диапазон частот этих головок находится в пределах от 90 до 12 000 Гц. Питание звуковых головок производится от усилителя типа УМ-50А. В качестве задающего генератора используется звуковой генератор типа ГЗ-18. Приемно-регистрирующая аппаратура включает датчик давления и компьютер. Воспринимающей частью датчика является полый шарик пьезокерамики, имеющий диаметр 7 мм и толщину стенки 0,25 мм. Размеры чувствительного элемента датчика выбираются так, чтобы они были на порядок меньше измеряемых длин волн, во избежание искажений звукового поля.

Методика проведения экспериментов

В работе с помощью электродинамического излучателя возбуждаются колебания определенной частоты в заданном диапазоне. Для получения акустических характеристик камеры в различные моменты работы двигателя опыты проводятся с несколькими макетами заряда, имеющими различные размеры (имитирующие выгорание заряда). Для каждого варианта газовой полости настройкой звукового генератора снимается амплитудно-частотная характеристика в пределах первых двух резонансов продольной моды колебания. По амплитудно-частотной характеристике определяются собственные частоты камеры. На этих же частотах снимается распределение амплитуды колебательного давления для продольной моды колебаний с помощью датчика, перемещаемого по оси камеры.

Последовательность расчетов и обработки экспериментальных данных

I. Расчет акустических характеристик модельной камеры сгорания:

– определяются по формуле (32) низшие значения волнового числа k (с использованием вспомогательных таблиц) и подсчитываются собственные частоты продольных колебаний по формуле f=kc^

J 2n.

При подсчете частоты колебаний на акустической модельной установке, берется скорость звука в воздухе, а для натуральной камеры сгорания следует рассчитывать скорость звука в продуктах сгорания;

– рассчитывается амплитуда колебаний давления в относительных величинах (отнесенная к амплитуде давления p 0 при х = 0) по формулам (33)–(36), (рис. 2);

– приближенное определение потерь акустической энергии в камере сгорания. Потери акустической энергии, отнесенные к единице времени, dE / dt пропорциональны плотности энергии E . Обозначая коэффициент пропорциональности через 2δ, имеем dE / dt = 2δ E , откуда интегрируя находим

E = E0 exp (-25t), где E0 – плотность энергии в момент t = 0.

Амплитуда давления вследствие потерь в колебательной системе падает по экспоненциальной зависимости t         —5t

P = p 0 e .

Величина 5=

dE 2 Edt

является коэффициентом затухания для продольной моды и характеризует

потери акустической энергии в единицу времени. Приближенно коэффициент затухания δ можно определить, имея амплитудно-частотную характеристику колебательной системы, по значению добротности Q [2; 6]. Следует заметить, что Q это характеристика линейной системы с сосредоточенными параметрами, но условно Q может использоваться в качестве характеристики нелинейных систем с распределенными параметрами. Величина Q представляет отношение средней по времени располагаемой энергии к величине потери энергии за период колебаний [2; 6–8; 14–15], следовательно, Q = π или Q = ω , здесь T = π – период колебаний. Добротность колеба-δ⋅T          2δ            ω тельной системы, имея амплитудно-частотную характеристику, можно определить по ширине

2                                f ^x

.

кривой (рис. 3) ( f 1 – f 2 ) на уровне, равном     p , по формуле Q =

2 max                       f _{2 -} f

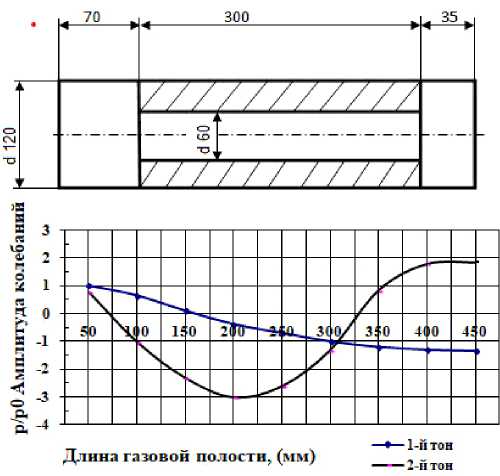
Рис. 2. Распределение колебательного давления в газовой полости камеры (по расчетным данным):

1 – первый тон продольной моды; 2 – второй тон продольной моды

• Fig. 2.    Distribution of vibrational pressure in the gas cavity of the chamber (according to calculated data):

1 – the first tone of the longitudinal mode; 2 – the second tone of the longitudinal mode

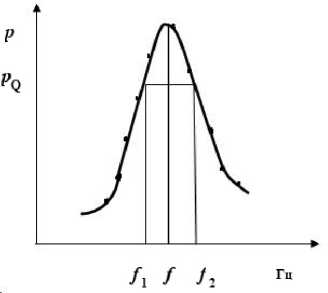
Рис. 3. Определение добротности Q по амплитудно-частотной характеристике колебательной системы

• Fig. 3.    Determination of the quality factor Q by the amplitude-frequency haracteristic of the oscillating system

Из приведенных выражений для Q получаем 5 = п ( f 2 - f 1 ) .

Если камеру сгорания заполнить газом с такими характеристиками, чтобы выполнялось соотношение

• ( RT ) k k k ₌ 1

(RT)mod kmod то в модельных экспериментах будут имитироваться частоты колебаний и характеристики потерь, близкие к имеющим место в камере сгорания работающего двигателя (считая потери с потоком через сопло малыми).

• II.    Построение акустических характеристик модельной камеры сгорания по экспериментальным данным.

• 1.    Строятся графики амплитудно-частотных характеристик камеры сгорания.

• 2.    Строится график собственной частоты колебаний камеры сгорания в функции отношения диаметра канала заряда к диаметру камеры сгорания.

• 3.    Строятся графики p / p 0 = f ( x ) для первого и второго тона продольной моды.

• 4.    Строится график коэффициента затухания в функции отношения диаметра канала заряда к диаметру камеры сгорания.

Заключение

Разработана методика расчетно-экспериментального приближенного определения акустических характеристик камер сгорания ракетных двигателей твердого топлива, без учета влияния горения твердого топлива. Учитывая большие затраты на создание Т-образной экспериментальной камеры сгорания РДТТ и значительные трудности проведения таких экспериментальных исследований, предложенный алгоритм позволяет менее затратно по времени и средствам определить частоты собственных акустических резонансов в полостях РДТТ, в частности для продольной моды, и выполнить прогноз их коэффициентов (декрементов) затухания.