Методика определения дальности полета частиц грунта при работе грунтомета

Введение . Лесное хозяйство Российской Федерации в настоящее время продолжает оставаться во многом слабой отраслью, требующей существенной модернизации и основных направлений деятельности с использованием современных инновационных научно-технических достижений [1].

В этой связи актуальным направлением является внедрение нового оборудования, малогабаритного по размерам и универсального по технологическому назначению. Одним из образцов такого рода оборудования являются грунтометы [2], область применения которых представлена на рис. 1.

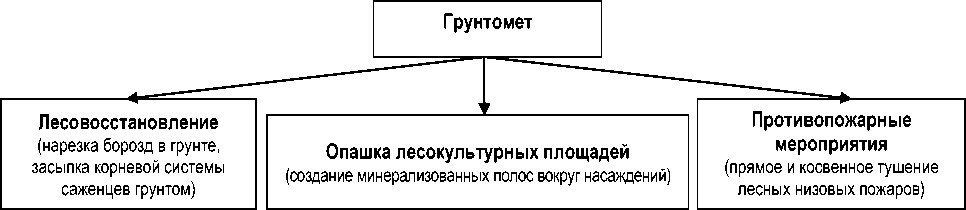
Рис. 1. Область применения грунтометов

В наше время в России и зарубежных странах широкое применение находят машины и оборудование с активными рабочими органами для проведения лесовосстановительных и лесохозяйственных работ путем нарезки борозд в грунте в сложных условиях движения оборудования, перемещения грунта для засыпки корневой системы саженца, опашки созданных лесокультурных площадей, а также проведения противопожарных мероприятий.

Материалы и методы исследований . При использовании грунтометов его фреза вырезает в грунте борозду определенной ширины [3], а вырезанный грунт, перемещаясь по лопаткам фрезы, откидывается (метается) на некоторое расстояние. Одним из вариантов определения этого расстояния служит построение траектории полета частиц свойств как самого грунта, так и свойств воздушной среды.

Для определения траектории полета частиц грунта в сопротивляющейся среде необходимо знать коэффициент сопротивления окружающей среды. С этой целью ведем коэффициент k , учитывающий сопротивление двух видов: ламинарное (рассчитываемое по формуле Стокса) и лобовое (рассчитываемое через миделево сечение). При этом для повышения точности расчетов процесс движения от момента слета частицы с лопатки и до момента падения на землю необходимо разделить на «n» равных по времени частей.

k со пр0

6 • п • n • r c • S • P в • V O m        2 • m

где n — вязкость воздуха, Па - с; r - радиус частицы грунта, м; е^ - коэффициент лобового сопротивления грунта; р - плотность воздуха, кг/м³; V_o - начальная скорость вылета частицы, м/с; S - миделево сечение частицы грунта, м; m – масса частицы грунта, определяемая из выражения (2).

4₃ m = — • п • r

.

Далее определим проекции ускорения а 0х , а 0у по выражению:

a0x =-VO • Cos(Vex ) • ксопр0, aOу = -g - V0 • Sin(Vex ) • kсопрО проекции скоростей V1x, V1y из выражения (4):

^V 1x = V O • ^Cos( V ex ) - V₀ • ^Cos( V ex ) • k conpO • ^ t, V iу = V o • Sin( V ex ) — V o • Sin( V ex ) • КорО • ^ — g • ^

где A t - шаг по времени, с.

Проекции скоростей S 1x , S 1y найдем из выражения (5):

S , x = 1 •A t - ( v , • Cos ( V ex ) - V , • Cos ( V cx ) • k 0 -A t )

S , у = 1 •A t - ( 2V , • Sin ( V ex ) - V , • Sin ( V cx ) • k , 0 •A t - g •A t )

Определим угол схода ф сх1 и V i с учетом их изменения за время A t по выражению:

V ex, = arctg

k

'   1

V ^v i x 7

• V , = J V + V .

Цикл (1)–(6) повторяется до тех пор, пока S ny , где n – количество шагов не станет меньше нуля. Далее определим дальность L и высоту H полета по выражению:

L = X S ix + S₂ x + S 3x + ... + S nx

H = max X S iy + S ,, + S 3, + ... + S„

На рисунках 2–3 представлены траектории полета частиц песка различного гранулометрического состава.

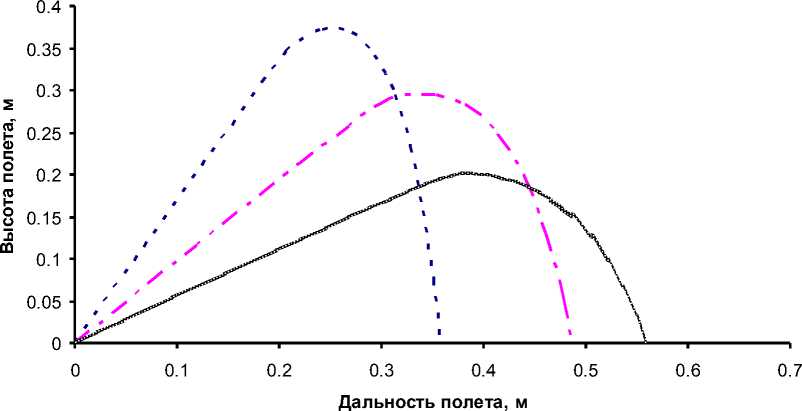
Угол вылета 60 градусов       Угол вылета 45 градусов       Угол вылета 30 градусов

Рис. 2. Траектория полета частиц грунта радиусом 0,12 мм

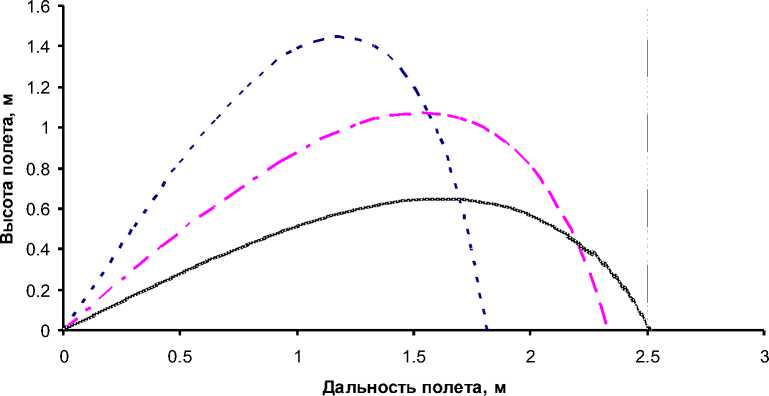
Угол вылета 60 градусов      Угол вылета 45 градусов      Угол вылета 30 градусов

Рис. 3. Траектория полета частиц грунта радиусом 0,25 мм

Из данных на рис. 2–3 видно, что дальность полета частиц грунта увеличивается при снижении значений угла схода частиц с лопатки рабочего органа. Высота полета при этом уменьшается. Все кривые по виду близки к параболе. Из-за сопротивления воздуха правое плечо параболы меньше левого, т.е. каждая кривая имеет вертикальную асимптоту. Если провести вертикальную прямую через точку максимального подъема частиц, то кривая правая ветка каждой кривой окажется ближе к этой вертикали, чем ее левая ветка (ввиду наличия сопротивления воздуха).

Воспользовавшись полученным циклом (выражения (1)-(6)), для частиц радиусом 0,00025 м траекторию полета графически представим на рис. 4, из диаграммы которого следует, что при увеличении угла наклона рабочего органа к обрабатываемой поверхности высота полета частиц увеличивается, а дальность - уменьшается. Для частиц данного типоразмера дальность полета частиц будет не меньше 1,6 м.

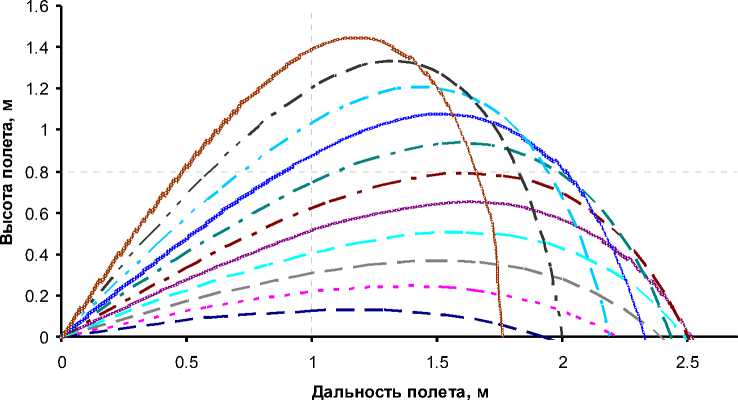
^м ^м Угол вылета 10 градусов ■ ■ ■ IУгол вылета 15 градусов ^^^Н ^^^Н Угол вылета 20 градусов ^^М ^М Угол вылета 25 градусов апяшваяпяя!Угол вылета 30 градусов ^^^ ■ ■ Угол вылета 35 градусов ^^^ ■ ■ Угол вылета 40 градусов uwwmKwuУгол вылета 45 градусов ^^М м Угол вылета 50 градусов ^^^ ■ ■ Угол вылета 55 градусов «мннмнммниУгол вылета 60 градусов

Рис. 4. Траектория полета частиц грунта радиусом 0,25 мм

Ввиду различных углов схода частиц с лопаток рабочего органа, а также того, что на практике грунт представляет собой совокупность частиц различных типоразмеров, частицы будут лететь по разным траекториям, на разных высотах и на разные расстояния. Следовательно, приземлившиеся частицы будут образовывать достаточно широкую (2,5–3 м) насыпную полосу. Зная состав минерализованного грунта по фракциям, можно рассчитать ширину этой полосы.

Выводы

• 1.    Представлена методика, позволяющая определить дальность и высоту полета частиц, сошедших с лопаток грунтомета.

• 2.    Графически показана зависимость траектории полета частиц от их размеров и начальных углов схода с лопаток грунтомета.