Методика определения момента трения в усовом манжетном уплотнении

Типичное манжетное уплотнение представляет собой конструкцию кольцеобразного вида, включающую в себя элементы как торцевого, так и радиального уплотнений[1-4]. Периферийная посадочная часть манжеты плавно переходит в тарельчатую упругую диафрагму с завулканизи-рованной в нее звездообразной пластинчатой или проволочной пружиной. Манжета имеет две уплотнительные кромки, из которых торцевая кромка прижата упругой резинометаллической диафрагмой, а радиальная - браслетной пружиной.

Плотность первоначального контакта в подвижном соединении, уплотненном манжетой, повышается с увеличением давления рабочей жидкости, которое прижимает уплотнительную губу манжеты к уплотняемой поверхности. Основное требование, предъявляемое к манжетам – обеспечение необходимой герметичности уплотняемого подвижного соединения при эксплуатации в течение заданного срока. Нарушение герметичности при эксплуатации зависит от многих факторов: радиального усилия прижатия контактной кромки уплотнительной губы манжеты к валу, геометрии эластичного элемента манжеты, скорости скольжения в уплотняемом подвижном соединении, температуры и давления рабочей жидкости, свойств уплотняемой среды и применяемого эластомера, шероховатости уплотняемого вала, статического и динамического эксцентриситета, монтажных дефектов и др.

Наиболее часто для герметизации вращающихся валов применяют эластомерные радиальные манжеты с пружинами и без пружин (рис.1), армированные и неармированные манжеты.

При повышенных давлениях следует применять опорный конус (рис.2, а), манжеты специальной усиленной конструкции (рис.2, б) или уплотнения с опорным конусом из фторопласта (рис. 2, в).

В расчета среднего контактного давления на элементы уплотняющей губки (рис. 3), для указанных тип уплотнений используют результирующее удельное контактное усилие, которое определяется по формуле [1]:

P = Pm + Ри + Pn + Pp, где Pm - удельная сила от растяжения губки манжеты;

P и - удельная сила от изгиба губки вследстви е эксцентриситета;

P n - удельная сила от растяжения пружины;

P p - удельная сила от давления жидкости и среды на профиль губки.

Здесь

^P p = 0,5( р ^- р_с ^{) 1 +} р_а ⁺

+ 0,5ph [1 -(pc Ip)(h2I h1)2]I1, где p – внутреннее давление рабочей среды; pc – внешнее давление; h1 и h2 – толщины пленки; l – ширина поверхности губки манжеты.

Тогда среднее контактное давление будет равно:

P pk =  = ^P M ^{+ Р} И ^{+ P} n ^{+ P}P ’

a где а – ширина кромки контактной поверхности; Pm , Ри, Pn, Pp - составляющие контактного

а)                     б)                     в)                    г)                д)

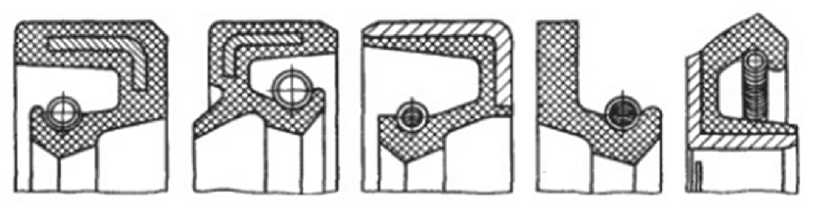
Рис. 1. Эластомерные радиальные манжеты с пружинами:

а – армированная; б – армированная с пыльником; в – армированная с открытым каркасом; г – неармированная; д – армированная с наружной кромки для уплотнения втулок

а)                            б)                         в)

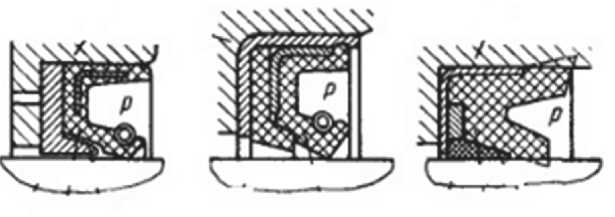
Рис. 2. Уплотнения, применяемые при повышенном давлении среды: a – стандартная манжета с опорным конусом (p<0,3 МПа);

б – манжета фирмы «Крейв пейхинг» (p<3,5 МПа);

в – манжета с конусом из фторопласта фирмы «Манвил» (p<2,1 Мпа)

давления соответственно от сил Р м , Р и , Р п , Р р . Таким образом, для нахождения момента тре-

ния, можно проинтегрировать среднее контакт-

ное давление:

l 1 л

l 1 п

Мтр = j J dMTP d^dz = j j pK fRdфdz,

о о

о о

Кроме рассмотренных типов манжетных уплотнений в работах [1-4], широкое распространение получило усовое манжетное уплотнение с расклинивающим подпружиненным

кольцом. В настоящее время в литературе не приводится какой либо методики его расчета. Актуальность создания такой методики возросла в последнее время, так как подобный тип уплотнения широко представлен в изделиях специальной техники, работающих в условиях криогенных температур.

Цель исследования: Разработка методики определения момента трения в радиальным манжетном уплотнении, образованном усовой манжетой с расклепывающим кольцом.

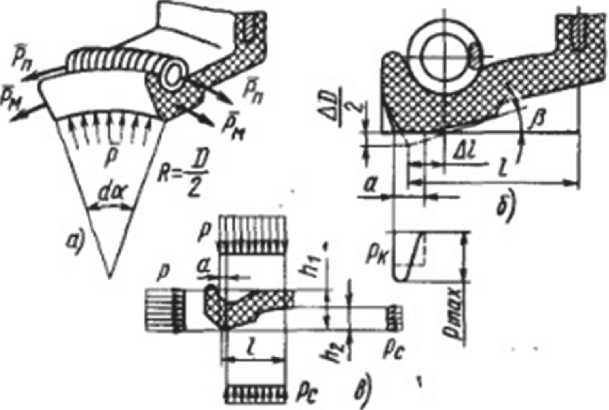
Рис. 3. Схема сил, действующих на элемент радиальной манжеты

ПОСТАНОВКА ЗАДАЧИ

Манжетное уплотнение представлено на рис. 4. Оно представляет собой усовую манжету, лепестки которой расклинены клиновидным кольцом с фиксированным усилием сжатой пружины. Вращающийся вал контактирует с внутренним лепестком манжеты. Материал манжеты и кольца – фторопласт-4. Манжетное уплотнение способно работать в диапазоне температур от минус 183 °С до плюс 250 °С.

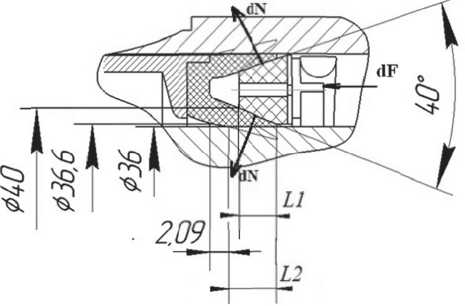
Рис. 4. Схема усового манжетного уплотнения с геометрическими параметрами

С целью упрощения расчетов принимаем следующие допущения: фторопластовую манжету считаем абсолютно эластичной и монтируемой на вал без предварительного натяга. Клиновидное кольцо, считаем недеформируемым. Трением данного кольца о лепестки манжеты пренебрегаем. Исходя из симметричности профиля кольца и лепестков манжеты, считаем нагрузку, приходящуюся на каждый лепесток, одинаковой.

Погонное усилие, действующей на кольцо, составляет dF . Следовательно, в нормальном направлении на каждый лепесток приходится усилие dN = dF /2.

Таким образом, задача может быть сведена к определению момента трения в зависимости от усилия F, которое изменяется в нашем случае в интервале 0…196 Н.

РАСЧЕТ МОМЕНТА ТРЕНИЯВ МАНЖЕТНОМ УПЛОТНЕНИИ

Общий момент трения для контактной по- верхности записывается в следующем виде:

Mtp

L _г 2 л

J J dM_TP d ^ dz ,

о о

Необходимые для расчета характерные размеры приведены на рис. 4.

Момент трения можно записать в следующем виде:

L 2 - П                     L 2 2 п

MTP = J J dMTPd^dz = J J PK fRdфdz‘ о о                       о о dN

2nRL_x ^.

где P_K =

После интегрирования при выбранных гра- ничных условиях получаем

, F  a   L7

MTP = —tg — fR -TP 2    2    Lx , где F – усилие, действующей на кольцо; f – коэффициент трения; R – радиус вала, L1- ширины участка контакта расклинивающего кольца с лепестками манжеты; L2– ширины кольцевого участка контакта лепестка манжеты с валом.

Для проверки аналитического метода расчет проведём численный эксперимент с помощью программного комплекса ANSYS.

РАСЧЕТ КОНТАКТНОГО ДАВЛЕНИЯ И МОМЕНТА ТРЕНИЯ В МАНЖЕТНОМ УПЛОТНЕНИИ С ПОМОЩЬЮ ANSYS

Для расчета контактных давлений манжетного уплотнения по известным геометрическим параметрам уплотнения была построены трехмерные модели манжетного уплотнения в пакете трёхмерного моделирования Unigraphics NX 9.0 и транслированы в программный модуль Workbench16.

С целью сокращения объема вычислений, в приведенных ниже расчетах используется небольшой фрагмент зацепления как показано на рис. 5. Это также обусловлено необходимостью использования достаточно мелких конечных элементов, позволяющих достигнуть требуемой точности картины НДС зоны контакта.

Расчёт контактных давлений в CAE-системе ANSYS производится на схематизированной модели манжетного уплотнения [5, 6]. В связи с этим для расчета использовали упрощенный вариант модели. Расчёт производится в модуле ANSYS static structural.

Результаты расчёта контактного давления показали, что натягом можно пренебречь, так как контактные давления, полученные от натяга, незначительные и практически не влияют на результат расчёта. При создании модели был выбран материал сталь12Х1810Т для вала, а для манжеты и клиновидного кольца – фторопласт-4. Модель была разбита на конечные элементы с использованием упорядоченной сетки, в местах контакта размер элемента был выбран 1 x 1 мм. Модель жестко закреплена по боковым поверхностям объема и в ходе решения использовалась не полная модель, а ее часть (сектор), на которую были наложены дополнительные условия циклической симметрии. Было приложено усилие F согласно схеме. Полученный

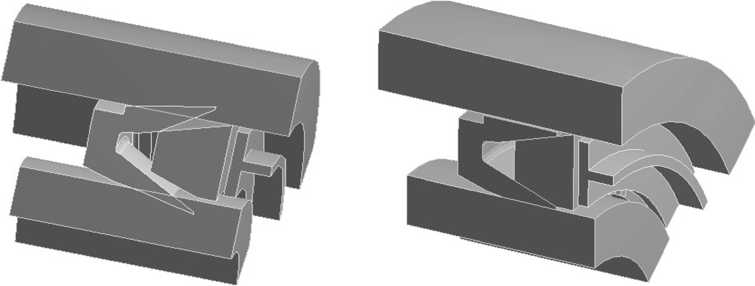
a)

б)

Рис. 5. 3D модель манжетного уплотнения: а – установка манжеты с натягом ; б – установка манжеты без натяга

результат моделирования и граничные условия показаны на рис. 6.

Были рассчитаны контактные давления, по которым определились нормальные усилия в каждом элементе, как произведение давление на площадь элемента. Общий момент трения в свою очередь, определялся, как сумма элементарных моментов трения, которые находились путем умножения значения нормального усилия на радиус вала и на коэффициент трения при соответствующей температуре. Расчетные значения момента трения М_ТР приведены в табл. 1и 2.

Указанный коэффициент трения f = 0,252 реализуется при криогенной температуре -183°С .

По полученным значениям, для всех возможных значений усилия F , построены графики изменения момента трения от усилия (рис. 7, 8).

Указанный коэффициент трения f =0,059 реализуется при нормальной температуре 20 ^оС.

Сравнение значений аналитического и числен -ного решений показывает, что погрешность не пре -высила 12 % для расчета с коэффициентом трения f = 0,252 и 10% с коэффициентом трения f = 0,059.

ЗАКЛЮЧЕНИЕ

Получено аналитическое выражение, позволяющее рассчитать момент трения в манжетном уплотнении вала, образованном усовой манжетой с расклинивающим кольцом. При этом в качестве аргумента функции использовано усилие прижатия кольца к манжете. Для назначенного диапазона усилий и двух значений коэффициента трения в паре сталь12Х1810Т и фторопласт-4 проведен сравнительный расчет моментных характеристик конкретного уплотнения с помощью аналитического и численного решений. Получен-

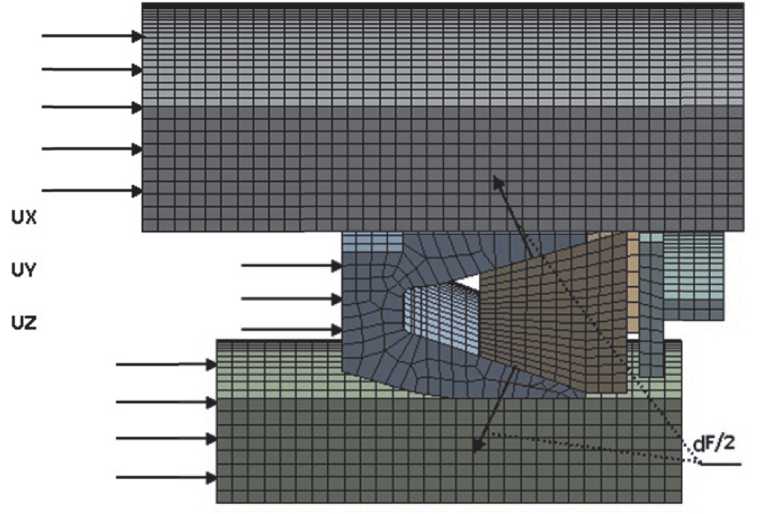
Рис. 6. Граничные условия и система нагружения манжетного уплотнения с помощью комплекса ANSYS

Таблица 1. Значения момента трения М_ТР для различных значении усилия F при коэффициенте трения f = 0,252

Усилие пружины F, Н	Момент трения М тр , Н^м (аналитическое решение)	Момент трения М тр , Н^м (численное решение)	Погрешность,%
0	0	0	0
49	0,09	0,1	10
98	0,18	0,2	10
147	0,27	0,3	10
196	0,36	0,4	10

Таблица 2. Значения момента трения М_ТР для различных значении усилия F при коэфициенте трения f =0,059

Усилие пружины F, Н	Момент трения М тр , №м (аналитическое решение)	Момент трения М тр , Н^м (численное решение)	Погрешность,%
0	0	0	0
49	0,09	0,1	10
98	0,18	0,2	10
147	0,27	0,3	10
196	0,36	0,4	10

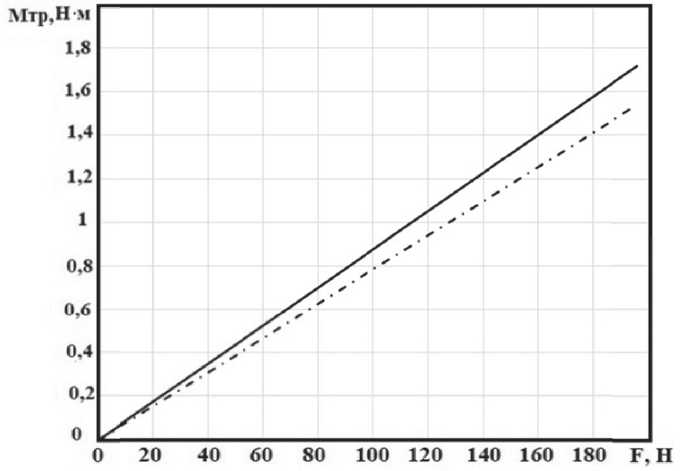
Рис. 7. Зависимость момента трения М_ТР от усилия F при коэффициенте трения f = 0,252: –––––––––––– численное решение; – ^. – ^. – ^. – ^. – аналитическое решение

ное расхождение методов не превысило 12%. В последующем расчетные данные могут быть использованы для анализа результатов экс-

периментального исследования данного типа манжетного уплотнения в условиях работы реального серийного узла.

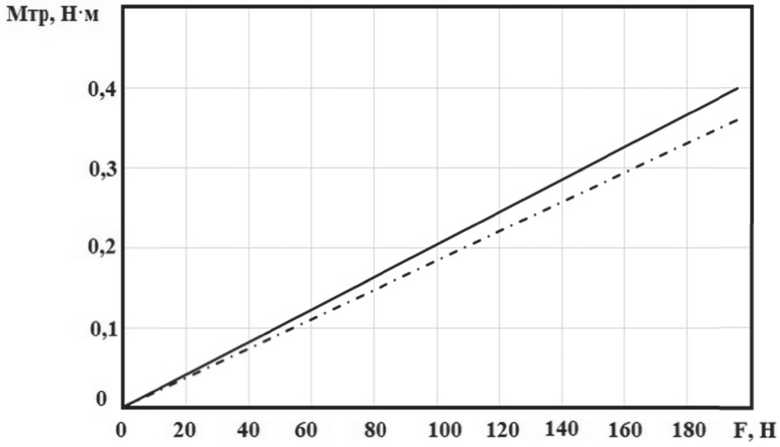
Рис. 8. Зависимость момента трения М_ТР от усилия F при коэффициенте трения f = 0,059: –––––––––––– численное решение; – ^. – ^. – ^. – ^. – аналитическое решение