Методика определения относительной среднеквадратической оценки искажений спектра сигнала с угловой модуляцией в цифровых синтезаторах с равномерной дискретизацией

Цитирование: Викторов, Д.С. Методика определения относительной среднеквадратической оценки искажений спектра сигнала с угловой модуляцией в цифровых синтезаторах с равномерной дискретизацией / Д.С. Викторов, Е.В. Пластинина // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(3). С. 259-271. DOI: 10.17516/1999-494X- 0261______________________________________________________________________________

Основными источниками искажений сигналов с угловой модуляцией (УМ), формируемых в цифровых синтезаторах (ЦС) с равномерной дискретизацией (РД), являются: ограничение минимального шага квантования фазы и напряжения, минимального тактового интервала дискретизации за счет ограниченного числа уровней квантования фазы и напряжения, частоты дискретизации, а также неравномерности амплитудно-частотной и фазочастотной характеристик интерполятора [1]. Для характеристики уровня искажений, возникающих при этом, используем относительную среднеквадратическую оценку (СКО) искажений

^Т U.                                       J ²

62 = г JU-(t)-U(t) dt = , , JIs-И"SM d®,

E о                  2ПE -j где U(t), U:(t) - исходный (идеальный) аналоговый и синтезируемый сигнал с УМ; S(to), Sс (to) -

^Т и .                                  ”,            . 1 2

Е = J U ( t ) dt = — J S ( to)| d to — энер- 0               2 n -J ¹

соответственно их спектры; т _и - длительность сигнала; гия исходного сигнала с УМ [1, 2].

На основе математических моделей цифровых и аналоговых сигналов с УМ, формируемых в ЦС с РД, проведем анализ спектров и определим относительную СКО искажений сигналов с УМ в зависимости от количества уровней квантования фазы и напряжения, частоты дискрети- зации и относительных параметров интерполятора.

В [2] показано, что все эквивалентные спектры Sэ(ю-nю3) с различными индексами n идентичны. Поэтому в дальнейшем будем рассматривать эквивалентный спектр Sэ(ю) при n=0. Было показано также, что квантование фазы и напряжения с УМ сигнала приводит к уменьшению амплитуды основной составляющей квантованного сигнала с УМ. Однако это изменение незначительно, следовательно, можно считать С1=U0/2.

Оценку искажения эквивалентного спектра цифрового сигнала с УМ, формируемого в цифровом синтезаторе отсчетов напряжения (ЦСОН) с РД, за счет дискретизации неквантованного сигнала с УМ можно получить из (1) в виде

0.5 ™ э

⁵ Т ( ю ■ ) = 2^ Л ⁵ »" U 0 *) Г d ™ -^{2 П} E - 0'5 ™ э

1 Г -™    , где S1(ю) = — J cosф(te  dt – спектр исходного сигнала с УМ.

Для достаточно большого класса реальных сигналов можно указать явную форму зависимости относительной СКО 52(to ) от частот дискретизации. Для сигналов, спектр ко-Тэ                                n торых, начиная с некоторого значения ю1 = nAf, спадает при ю^« быстрее, чем B /|ю| при n>1, где B - постоянная величина, относительная СКО 52,(юэ) определяется отношением [1]

5 Т ( ю э ) <

( f э / A f ) ^{-( 2} n ^{- 1 )}

2 n - 1

2 n - 1 — 2 ( n - 1)²

На рис. 1 приведены оценки (3) в зависимости от значения fэ/∆f для различных значе- ний n. 2

Расчет относительной СКО 5 _Т ( ю э ) в соответствии с (3) хотя и прост, но требует знания скорости спадания спектра, значения ∆ f и постоянного коэффициента B. Нахождение этих параметров на практике является трудоемкой задачей, а использование приближенных значений n , A f, B приводит к большим погрешностям в оценке 5 Т ( ю э ) .

Ниже будет получено выражение, позволяющее рассчитывать относительную СКО искажений 5 Т ( ю э ) более точно, чем (3), и не требующее знаний численных значений постоянных n, ∆ f , B.

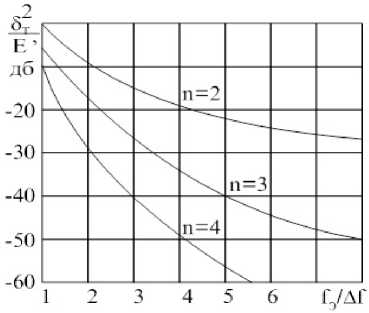
Рис. 1. Относительная СКО в зависимости от значения f э/ ∆ f для различных значений n

Fig. 1. Relative mean square assessment depending on value f э/ ∆ f for various values n

Подставляя форму эквивалентного спектра, образованного основными составляющими цифрового сигнала

•       /                        X

⁵ „ 1 (_Ш - n _m „ ) =

E C 1 5 ± [ m- ( n + l ) m „ ], < ! =-»

при |to - n го „ | < 0,5 to _э ;

0, при |to- nto3| > 0,5to„ в (2) и учитывая при этом, что 0,5 [551+ (го) + .5 (to)]= 51 (го), получим

^{0,5 ю} =

- (_И) = UL Т t S /»- m го , ) d го ^{2п E} -0,5ш, m =—". m *0

э

=—та, m *0

Используя неравенство ную СКО искажений можно

Е ak k

< ^ | a и делая замену переменных ю = ю - m ю₃ , относитель- k ^э

получить в виде неравенства

„ тт 2 ( m + 0,5 ) го             ²

52 к)< Е U^  J  I S (го) dго = m ^"*02ПE (m—^J    '

2nE

⁵ ,

U

Г^ d -J W d... , _м>d .

—c

Правая часть неравенства (5) равна энергии сигнала в интервале частот юг[ -0,5 ю _э , 0,5 ю _э ].

В большинстве случаев относительную СКО 5 2 ( to ) удобнее находить через энергию сигнала Тэ

Е _т , заключенную в интервале частот юе[ -0,5 ю _э , 0,5 ю _э ]. Тогда

5 2 ( го ) < '

T^v э    2п E

",            „2              5. ’          „2

= 1 — E T / E.

j | S 1 ( го ) d го— J | S 1 ( го ) d го

—та                          — 0,5 го _э

В современных радиолокационных стациях (РЛС), оконечные каскады передающих устройств которых работают в нелинейном режиме, используются сигналы с УМ и прямоугольной огибающей. Энергия такого сигнала равна Е = U о ² Т ц /2, где U о , T u - амплитуда и длительность радиоимпульса с УМ. В этом случае относительную СКО 5 ^ ( to ₃ ) можно записать в виде

⁵ T ^(го. )<¹ -пТ ; I 2 d ^го =¹ -пТ ; ‘ Г 1^Н² d ^{го                    (6)}

Так как эквивалентные спектры S ( го — n го ) с различными значениями n идентичны и отличаются лишь несущей частотой, то данная оценка справедлива для каждого из них.

Подставляя первое слагаемое из равенства

^

Е {с 1 >V[®- ®0 - (n + l)®Э] + l=-”

^ Э ( ®- n ® Э ) = •

»

+   Е„mM+1 ^ mM+1[® ®0 (n + l)® э ]}, m=-^, m ^0

при ® - n ® _Э | < 0,5 ® _Э ;

0,            при |®- n®Э| > 0,5®Э в (1), где спектр исходного сигнала определяется в виде 5(ш) = 0,5U05 1+(to-to0), делая замену переменных ω=ω–ω0–mωэ и проводя аналогичные преобразования, можно получить относительную СКО 5Т(to3) для цифрового синтезатора отсчетов фазы (ЦСОФ) с РД в виде

5 T (_ю) = 1 - 2 | ’ | 5 »| 2 d ш                                           (7)

э        ^ПТ и 0

Так как $ (_Ю) = 0,5 [ 5 » + 5 1»^] и ^ + 4 |² = ^ ² + | 4 |² + 2Re A4 ’, то правые части выражений (6) и (7) равны. Следовательно, относительные СКО искажений О Т ( to ) эквивалентных спектров в ЦСОН и ЦСОФ с равномерной дискретизациями равны. Как видно из (6) и (7), от-2

носительная СКО оТ(Юэ) зависит как от частоты дискретизацией юэ, так и от формы спектра, т.е. фазовой структуры сигнала с УМ. Поэтому оценку ее необходимо производить для каждого вида группы сигналов.

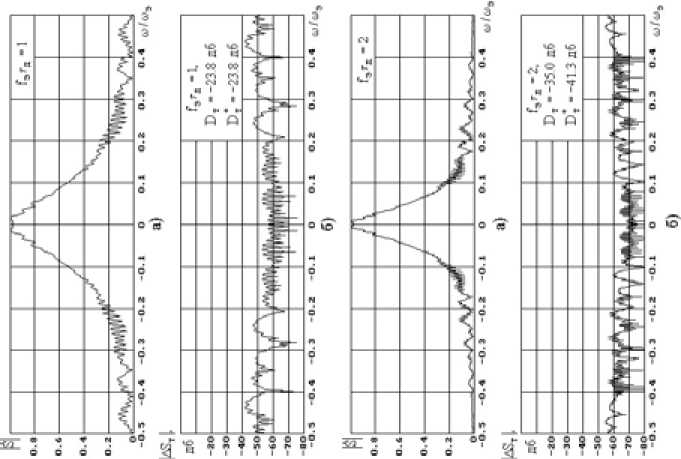
Графики относительной СКО О Т ( to ₃ ) для линейно-частотной модуляции (ЛЧМ) сигналов с различной базой n с в зависимости от значения f э/ ∆ f , где f э частота дискретизации, ∆ f – девиация ЛЧМ сигнала, приведены на рис. 2. Там видим, что для получения достаточно малых искажений частоту дискретизации следует выбирать значительно больше девиации ЛЧМ сигнала. При увеличении базы ЛЧМ сигнала вдвое для одинаковых соотношений / э/ А f величина 5 2 ( to, ) Тэ уменьшается приблизительно на 3 дБ.

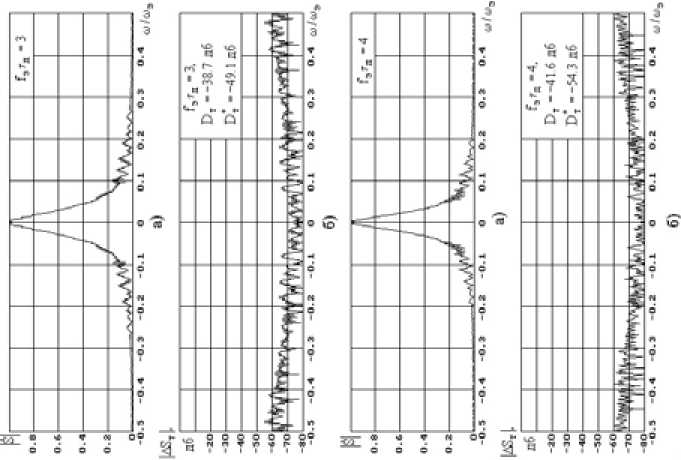
Для получения малого уровня боковых лепестков в функции неопределенности сигнала с УМ и прямоугольной огибающей в радиолокации могут использоваться сигналы с нелинейной частотой модуляции [3, 4]. На рис. 3 а в качестве примера приведена кусочно-линейная функция, описывающая закон изменения фазы нелинейно-частотной модуляции (НЧМ) сигнала. Закон изменения фазы ϕ ( t ) симметричен относительно оси координат, и на рис. 3 а изображен график только правой его половины. Графики модуля спектра такого НЧМ сигнала изображены на рис. 3 б , а зависимость относительной СКО О Т ( to ₃ ) от значения / э т _д , где т _д - длительность одной дискреты, приведена на рис. 4.

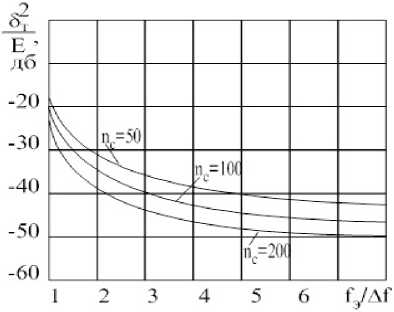
Рис. 2. Относительная СКО для линейно-частотной модуляции (ЛЧМ) сигналов с различной базой n _с, в зависимости от значения f э / ∆ f

Fig. 2. Relative mean square assessment for linearly-frequency modulation of signals with various base n c depending on value f э/ ∆ f

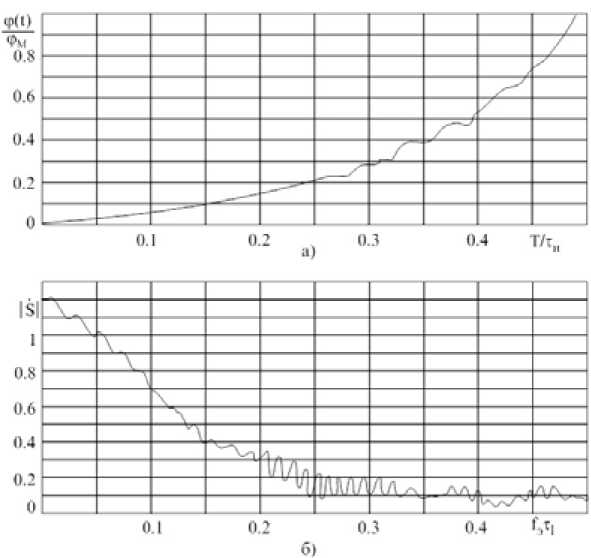
Рис. 3. Кусочно-линейная функция, описывающая закон изменения фазы нелинейно-частотной модуляции сигнала (а). Модуль спектра НЧМ сигнала (б)

• Fig. 3.    а) The piecewise linear function describing the law of change of a phase of nonlinear and frequency modulation of a signal; б) Module of a range of nonlinear and frequency modulation of a signal

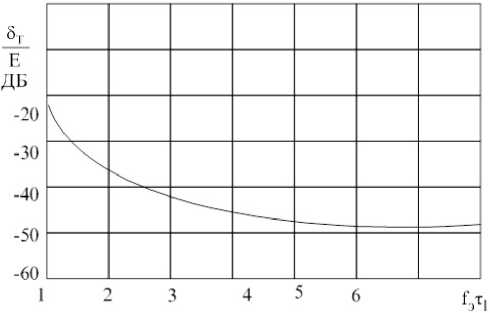
Рис. 4. Относительная СКО в зависимости от значения f э τ д

• Fig. 4.    Relative mean square assessment depending on value f э τ д

Относительная СКО искажений 5 Т (( О ) , как следует из (2), представляет собой относительную интегральную оценку энергии всех паразитных составляющих эквивалентного спектра, возникающих при дискретизации сигнала с УМ, спектр которого не является финитным. В то же время значительный интерес вызывает распределение энергии этих искажений в диапазоне частот эквивалентного спектра.

Спектр сигналов с УМ в общем случае не является финитным. При правильно выбранной частоте дискретизации (или эффективной ширины спектра) основная доля энергии формируемого сигнала с УМ содержится в диапазоне частот эквивалентного спектра. Незначительная же часть энергии 5Т(to,) содержится в “хвостах” спектра. При этом уровень спектральной плотности сигнала с УМ вне диапазона частот эквивалентного спектра, как правило, уменьшается с увеличением расстройки по частоте относительно несущей частоты сигнала с УМ. Поэтому можно предположить, что при дискретизации сигнала с УМ это приведет к тому, что уровень спектральной плотности искажений ASт (ю) эквивалентного спектра, возникающих при этом, Т будет уменьшаться к центральной частоте эквивалентного спектра относительно ее уровня на граничных частотах. Для подтверждения этого предположения приведем расчет искажений ASТ (ю) численным методом в соответствии с выражением

.     /                     X         .     /                     X         . /

A S т ( n to , / N ) = S э ( n toэ I N ) — S ( n го э I N ) ,                                   (8)

где >V n ^to э /^N ) - значения коэффициентов дискретного преобразования Фурье (ДПФ) исследуемого сигнала с УМ; S ( n to _э I N ) - отсчеты спектральной плотности аналогового сигнала с УМ на дискретных частотах n ю э / N .

На рис. 5 – 9 изображены графики модулей прямой составляющей спектра ЛЧМ-сигналов |S ( to ) и соответствующих искажений эквивалентного спектра | A S _т ( to ) для различных значений базы ЛЧМ-сигнала n _с и отношений частоты дискретизации к девиации ЛЧМ сигнала f/ A f.

На рис. 9 аналогичные графики изображены для сигнала с нелинейной частотой модуляции для различных соотношений f т _д , где т _д - длительность одной дискреты НЧМ-сигнала (рис. 3).                                                                                                          ₂

Неравенства (6) и (7) определяют верхнее значение относительной СКО искажений 5 2 ( to, ) .

₂                              Тэ

Для сравнения, насколько точно эти оценки 5dto ) соответствуют их действительным значе-э ниям для различных видов сигналов с УМ и заданными параметрами, они были рассчитаны численным методом в виде

$ Т ( to . ) -ЁА s Т ( nto . I N ) ,                                                (9)

'

где значения |AS,(nе,, /N) определяются из (8). Значения относительной СКО искажений Dm=10lg5т2(юэ) для заданных значений параметров сигналов с УМ приведены на рис. 5 - 9. Сравнивая эти значения с аналогичными значениями относительной СКО 52(to ), полученных Тэ для соответствующих параметров сигнала с УМ из графиков (рис. 2), можно сделать вывод, что они практически совпадают. Следовательно, при вычислении относительной СКО искажений 2

5 _Т ( to , ) в соответствии с (6) и (7) знак неравенства в этих выражениях можно опустить.

Сравнивая графики 5 Т ( to , ) на рис. 2 и 3 с графиками на рис. 1 и учитывая сказанное выше, можно сделать вывод, что выражения (6) и (7) позволяют рассчитывать относительную СКО искажений ₈ Т ( to , ) более точно, чем выражение (3), полученное в _И.

Как видно на рис. 5 – 9, спектральная плотность искажений дискретизированного сигнала с УМ неравномерно распределена в диапазоне частот эквивалентного спектра. Ее уровень на центральной частоте эквивалентного спектра ю =0 приблизительно на 15 дБ меньше, чем на граничных частотах |ю| = ± 0,5 ю _э . Для упрощения дальнейших расчетов аппроксимируем распределение спектральной плотности искажений |A S _т ( ю ) | ² аналитической функцией. Заметим,

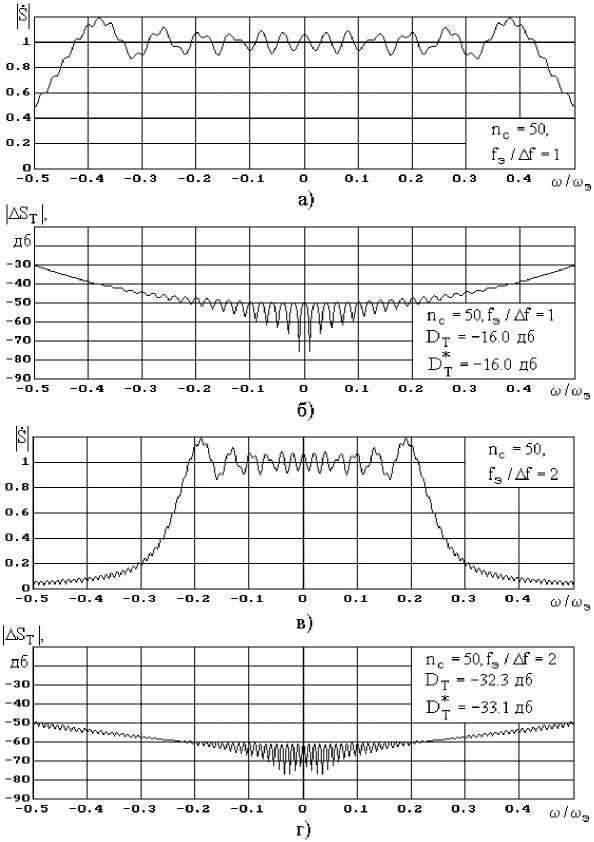
Рис. 5. Модули прямой составляющей спектра ЛЧМ сигналов |, У ( ю )| и соответствующие искажения эквивалентного спектра | А У Т ( ю )| для различных значений базы ЛчМ сигнала n _с и отношений частоты дискретизации к девиации ЛЧМ сигнала f э/∆ f

• Fig. 5.    Modules of a direct component of a range of linear and frequency-modulated signals |> У (ю)1 and the corresponding distortions of an equivalent range | А У Т ( m )| for various base of linear and frequency-modulated signal n c and sampling frequency relations to deviation of linear and frequency-modulated signal f э/∆ f

что на рис. 5 - 9 уменьшение уровня спектральной плотности |a S _т ( ю ) | к центральной частоте эквивалентного спектра происходит практически линейно. Поэтому можно записать

_W™L = 101g ^ +  2 М ₊11

Е              Е lg2 ( ®э   J или

1.„,„ „г,2 ь..;

Y

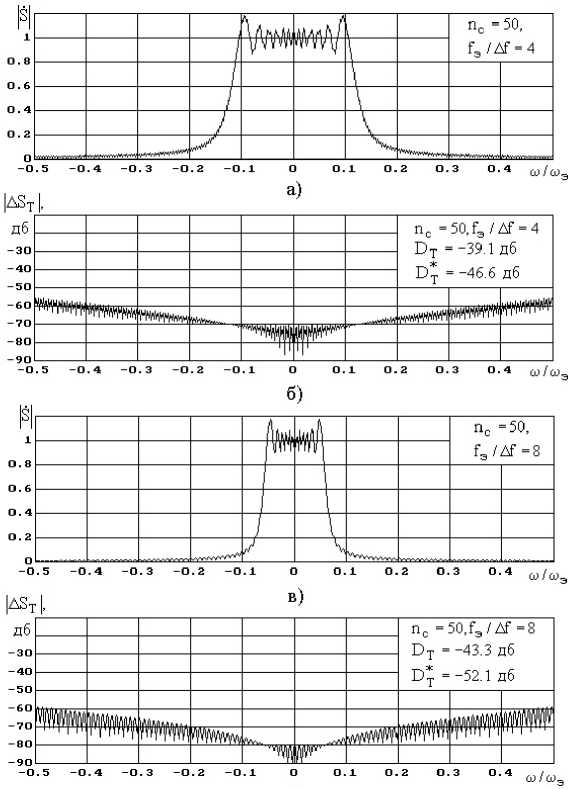
Рис. 6. Модули прямой составляющей спектра ЛЧМ сигналов 1/&(ю)| и соответствующие искажения эквивалентного спектра |л/ & Т (щ)| для различных значений базы ЛЧМ сигнала n _с и отношений частоты дискретизации к девиации ЛЧМ сигнала f э/ А f

• Fig. 6.    Modules of a direct component of a range of linear and frequency-modulated signals | S ( ffl )l and the corresponding distortions of an equivalent range |л £ Т ( m )| for various base of linear and frequency-modulated signal n _c and sampling frequency relations to deviation of linear and frequency-modulated signal f э/ A f

  1,5 где Y =     ;

  lg2

  
  

| A S т ( 0 ) 2 = const = |A S t ( 0 ) ² = _o.

В данном выражении неизвестно значение |ASт(0) |2. Ее значение можно определить из со- отношения 5Т (®э) = 1 -

1 ⁰ ’5“ э             2

— I S_t ( ® ) d ® . Решая данное уравнение, получим п Е о

I ASт (0) 2

3>j E Y +1

f э

2 r+ i

^^^^^^е

.

							nc = 100,f3/Af = 4 DT--42 1a6 DT-"49.5 Д6
ww								Ж*
				-W/'r

-0.5  -0.4  -0.3  -0.2  -0.1 О 0.1   0.2   0.3   0.4

-0.5  -0.4  -0.3  -0.2  -0.1 О

0.1   0.2   0.3   0.4

г)

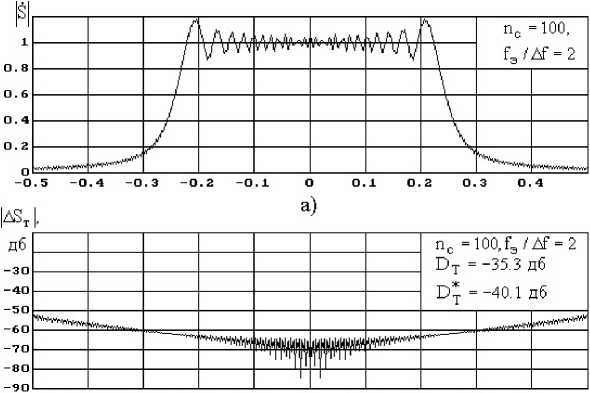
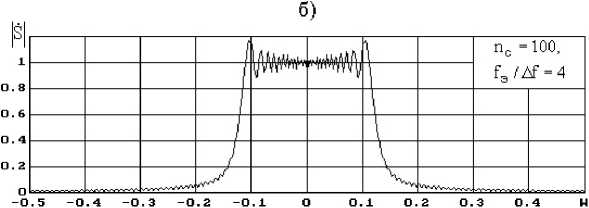
Рис. 7. Модули прямой составляющей спектра ЛЧМ сигналов 1, У ( ю ) и соответствующие искажения эквивалентного спектра A S Т ( m ) для различных значений базы ЛчМ сигнала n _с и отношений частоты дискретизации к девиации ЛЧМ сигнала f э/ ∆ f

• Fig. 7.    Modules of a direct component of a range of linear and frequency-modulated signals |/&( ю ) and the corresponding distortions of an equivalent range | A S Т ( m ) for various base of linear and frequency-modulated signal n c and sampling frequency relations to deviation of linear and frequency-modulated signal f э/ ∆ f

Следовательно,

\ (_m) ² = № ^(y+ 1X21 ®l / ^ю э ^{+ 1 ) Y} f .            ^{2 Y+ 1} - ¹

Данное выражение аппроксимирует распределение спектральной плотности искажений | A^ S Т ( m ) в диапазоне частот эквивалентного спектра.

Получено интегральное выражение, позволяющее рассчитать в ЦС с РД с достаточной для инженерной практики точностью относительную СКО искажений спектра, обусловленных

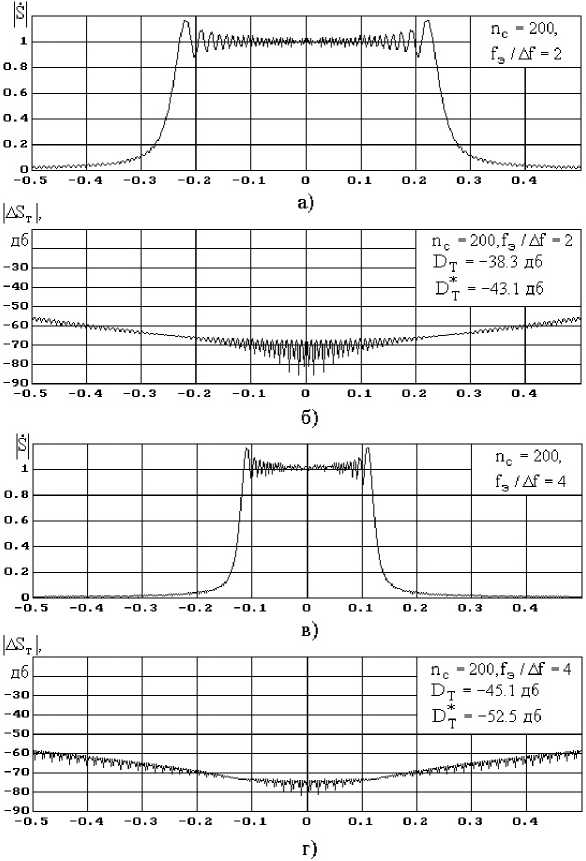
Рис. 8. Модули прямой составляющей спектра ЛЧМ сигналов |/& ( ю )| и соответствующие искажения эквивалентного спектра |a S Т ( ю )| для различных значений базы ЛчМ сигнала n _с и отношений частоты дискретизации к девиации ЛЧМ сигнала f э/ ∆ f

• Fig. 8.    Modules of a direct component of a range of linear and frequency-modulated signals |> У ( ю )1 and the corresponding distortions of an equivalent range | A S Т ( m )| for various base of linear and frequency-modulated signal n c and sampling frequency relations to deviation of linear and frequency-modulated signal f э/ ∆ f

дискретизацией неквантованного сигнала с УМ. Показано, что значение этой СКО зависит от вида сигнала с УМ и частоты дискретизации. Для двух видов сигналов, с линейной и нелинейной частотной модуляциями, рассчитаны зависимости, дающее возможность по заданному значению относительной СКО искажений сигналов определить необходимую частоту дискретизации. Установлено, что уровень спектральной плотности таких искажений эквивалентного спектра неравномерен и имеет спад к его центральной частоте. Получено выражение, аппроксимирующее уровень спектральной плотности этих искажений.