Методика определения положения метеорологической ракеты в пространстве

В процессе полёта метеорологической ракеты происходит её вращение вокруг продольной оси. Скорость данного вращения может достигать 300‒ 600 об/мин и сопровождаться прецессией оси. Для расшифровки результатов измерений научной ап-паратуры необходима информация о положении ракеты в каждый момент времени. Для этого могут использоваться следующие методы:            - нове гироскопической системы либо методы с ис-1 пользованием привязки к внешней среде.

Цена гироскопической системы, сохраняю-щей стабилизацию при такой скорости вращения объекта (ракеты), крайне высока. Кроме того, со -временные гироскопы не обеспечивают высокую точность, необходимую при проведении испытаний с использованием научной аппаратуры, из-за нака-пливания ошибки в их показаниях (дрейфа оси).

Рассмотрим методы привязки к внешней сре-де . Одним из возможных вариантов решения про-блемы может являться оптическая привязка к внешней среде. Данный вариант является трудным в реализации, поскольку зависит от множества внешних дестабилизирующих факторов :       - димо обеспечить работу системы в любых метео-рологических условиях, при любой облачности,в любое время суток. Также принципиальной про- блемой является отсутствие постоянного объекта привязки, поскольку ни одно из небесных тел не может обеспечить выполнение всех приведённых 2

выше условии.

Другим вариантом определения положения ракеты в пространстве может служить измерение вектора магнитного поля. Но такая методика также не является оптимальной, поскольку величина вектора напрямую зависит от магнитного поля земли в точке старта (её географического положе-НИЯ)и, следовательно, не может обеспечить уни-версальность методики. Кроме того, существует ряд факторов, влияющих на измеряемый вектор магнитного поля :                      ; магнит- ные аномалии, вызываемые залежами ископаемых РУД ; искусственно создаваемые магнитные поля (в случае наличия рядом, например , ускорительной техники), собственные магнитные моменты, соз-даваемые ракетой. Направление вектора магнитно-го поля меняется с высотой.

Исходя из приведённого выше анализа, был применён наиболее простой и эффективный метод решения данной задачи. Используемый метод ос-новывается на применении датчика линейных ус-корений. В данном случае удобно ввести цилинд-рическую систему координат (рис. 1).

Методика определения положения метеорологической ракеты в пространстве

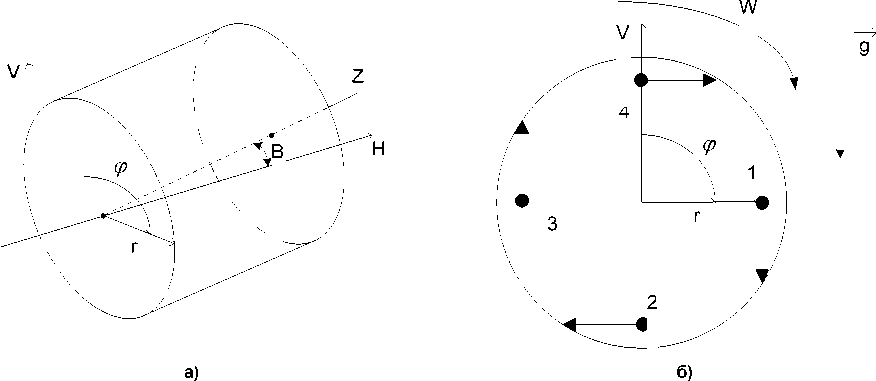
Рис. 1. Введённая цилиндрическая система координат

Ось Z системы координат сонаправлена с продольной осью ракеты; ось H ‒ ось, являющаяся проекцией оси Z на горизонтальную плоскость; Ф‒ угол отклонения от вертикальной оси в плос-КОСТИ, представленной на рис. 1, б; r ‒ расстояние до точки в плоскости перпендикулярной Z (см. рис. 1, а); V ‒ вертикальная ось ракеты.

Для привязки положения датчика (положения его оси) к системе координат связанной с ракетой рассмотрим сначала, плоскость, представленную на рис. 1, б(при горизонтальном положении раке-ты). Ось измерения датчиком показана вектором для разных положений ракеты.

Из рисунка видно, что датчик будет показы-вать значения, соответствующие ускорению 9,8 м/с² (далее 1 g ) в положении 1, ускорение, соответст-вующее ‒1 g в положении 3, и значения, соответст-вующие 0 g в положениях 2и 4. Поскольку ракета будет вращаться в плоскости, представленной на рис. 1, б, то линейное ускорение будет выражаться

:

a g sin(W t) , где W ‒ частота вращения ракеты вокруг оси Z; a ‒ линейное ускорение, измеряемое датчиком (понятно, что данная формула справедлива лишь для равномерно вращающейся ракеты вокруг сво-ей оси).

Разумеется, при движении ракеты в простран-стве угол отклонения её оси Z от горизонтального положения будет отличным от нуля. Для учёта данного отклонения используется следующая за-:

a g sin(W t) cos B , где W ‒ частота вращения ракеты вокруг оси Z; B ‒ угол отклонения оси Z от горизонтального положения (оси H) (см. рис. 1, а).

Рассмотрим вид сигнала, выдаваемый датчи-ком при движении ракеты в пространстве. Схема-тическое изображение данного сигнала представ-ле но на рис. 2.

Фаза несущей сигнала будет соответствовать углу поворота ракеты вокруг своей оси, амплитуда несущей даст информацию об угле наклона оси Z ракеты относительно горизонтального направления.

Явление прецессии при полёте ракеты приве-дёт к амплитудно -модулированному сигналу на выходе датчика (см. рис. 2). Информация о вели-чине и частоте прецессии оси отражена в глубине

L-K модуляции ---- и частоте модулирующего сиг-

L+K

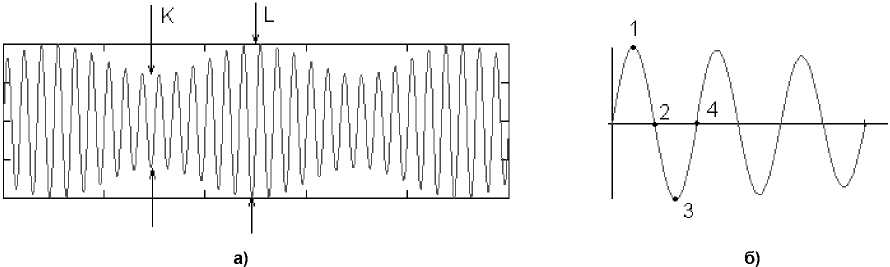
Рис. 2. Схематическое изображение сигнала: ‒ на длительном временном интервале; б‒ на коротком временном интервале

Серия «Компьютерные технологии, управление, радиоэлектроника», выпуск 14

Е. . Безукладников,А.Н.

нала. Угол прецессии продольной оси ракеты мо-

:

• L - K

Т I V tg B tg a ,

LK где а ‒ угол прецессии продольной оси ракеты (оси Z).

Для выполнения применимости выбранной нами методики определения положения ракеты в пространстве необходимо соблюдение следующих :

• 1)    частота прецессии продольной оси ракеты должна быть в несколько раз меньше частоты вращения ракеты вокруг продольной оси, в про-тивном случае будет довольно сложно выделить модулирующее колебание и несущую из получен-ного сигнала;

• 2)    положение ракеты должно быть отличным от вертикального, иначе в отсутствие прецессии оси значения проекций ускорения на ось измере-ния датчика будут равны нулю ;

• 3)    ракета не должна двигаться только за счёт сил инерции (например, быть в свободном падении), или же датчик будет в состоянии невесомости;

• 4)    следует учитывать уменьшение ускорения свободного падения с увеличением высоты полёта ракеты .

Заключение

Выбранная нами методика измерений позво-лит передавать всего по одному телеметрическому каналу данные об угле поворота ракеты вокруг собственной оси в любой момент времени, угле наклона оси ракеты относительно горизонтальной плоскости, угловой скорости вращения вокруг продольной оси, величине и угловой скорости прецессии оси Z ракеты вокруг продольной оси.