Методика определения пространственного положения недеформируемой конструкции космического аппарата

Введение. При использовании в составе космического аппарата крупногабаритных трансформируемых антенн (КТА) – рефлектора и облучателя, для обеспечения заданной точности наведения главного луча и формирования требуемой диаграммы направленности антенны, необходимо использовать периодическую корректировку положения рефлектора в условиях эксплуатации на орбите. В результате деформаций и смещений рефлектора, а также смещений облучателя КТА изменяются их положения в некоторой заданной системе координат (СК). Смещение рефлектора и облучателя относительно положения, заданного конструкторской документацией, влечет ухудшение радиотехнических характеристик антенны. Искажение формы и положения поверхности рефлектора, а также смещение при раскрытии облучателя КТА является результатом различных погрешностей взаимного расположения (погрешности, связанные температурными деформациями конструкции рефлектора; погрешности, связанные с деградацией материалов; погрешности, вызванные ошибками раскрытия конструкций КТА; погрешности изготовления конструкций и др.). Влияние на качество радиотехнических характеристик КТА оказывает результат взаимного расположения облучателя и рефлектора после их раскрытия в начальных режимах космического аппарата, что связано с разделенной наземной экспериментальной отработкой штанги, облучателя и рефлектора КТА [1–4].

Для выполнения задач корректировки положения рефлектора КТА необходимо с высокой точностью определить геометрические параметры взаимного расположения рефлектора и облучателя. Геометрическими параметрами являются расстояние между фокусом рефлектора и фазовым центром облучателя, а также ориентация фокальной оси рефлектора. Для определения геометрических параметров КТА необходимо определять пространственное положение ее рефлектора и облучателя. Для выполнения задачи определения положения конструкций КТА космический аппарат, имеющий в своем составе подобные антенные системы, необходимо оснащать системой контроля геометрических параметров (СКГП) КТА [5–7].

Состав СКГП и назначение ее элементов. В состав СКГП должны входить следующие элементы [8]:

– лазерный сканер;

– углоизмерительный прибор;

– светоотражательные элементы (СЭ);

– программное обеспечение.

Лазерный сканер определяет и выдает в бортовой вычислительный комплекс информацию о сферических координатах (расстояние и углы направления) СЭ, находящихся в его зоне действия, в системе координат, связанной с посадочной плоскостью прибора [9].

Углоизмерительный прибор (УП) предназначен для определения и выдачи в бортовой вычислительный комплекс информации об углах направления на СЭ, находящихся в его поле зрения, в СК, связанной с посадочной плоскостью прибора.

СЭ отражает падающее на него излучение в обратном направлении. По измеренным сферическим координатам СЭ вычисляются декартовые координаты контролируемых точек поверхности рефлектора и облучателя КТА.

Программное обеспечение СКГП выполняет следующие задачи: организация режимов работы системы и считывания информации с включенной бортовой аппаратуры, формирование команд для организации режимов и перехода между ними, вычисление пространственных координат КТ поверхностей рефлектора и облучателя КТА по измерениям СКГП, вычисление геометрических параметров КТА, формирование программной телеметрической информации, диагностика СКГП и ее оборудования и др.

На основе измерений БА вычисляются пространственные координаты контролируемых точек поверхностей конструкций КТА. Затем по вычисленным координатам этих точек определяется положение СК рефлектора и СК облучателя в некоторой базовой СК, позволяя затем определить геометрические параметры КТА. Ниже будет представлена методика определения положения недеформируемой конструкции КТА. Недеформируемой конструкцией считается любая конструкция, поверхность которой в процессе эксплуатации не подвержена искажению и принадлежащие ей точки не изменяют своего положения

(в пределах заданного допуска) относительно начального. В данном случае недеформируемой конструкцией считается облучатель КТА. СК облучателя определяется по вычисленному массиву пространственных координат СЭ, расположенных на его корпусе, с помощью измерений одного УП и знания расстояний между измеряемыми СЭ.

Описание методики определения положения недеформируемой конструкции. Рассмотрим данный алгоритм на примере трех СЭ. В трех вершинах G 1, G 2 и G 3 пирамиды, представленной на рисунке, расположены СЭ. Вершина пирамиды ( O ) является центром СК УП. Стороны пирамиды, находящиеся между центром СК УП и соответствующими СЭ, являются ребрами пирамиды и, соответственно, искомыми расстояниями. Эти расстояния необходимы для определения пространственных координат СЭ в СК УП. Найденные пространственные координаты СЭ в СК УП однозначно можно пересчитать в базовую СК, зная положение СК УП в базовой СК [10].

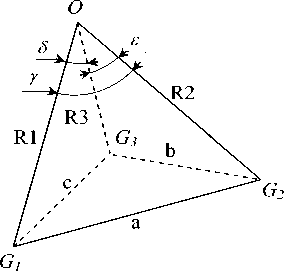
Геометрическое представление задачи

Совокупность каждой пары ребер и стороны основания пирамиды образуют треугольник. По теореме косинусов в трех треугольниках, которые являются гранями пирамиды, существуют уравнения связи (1) между их сторонами:

a ² = R ² + R 2 - 2 ■ R₁ ■ R ₂ ■ cos( Y ), b ² = R 2 + R 3 — 2 ■ R 2 ■ R з ■ cos( s ), c ² = R ² + R 2 — 2 ■ R₁ ■ R 3 ■ cos( 5 ),

где a, b, с – стороны треугольников, образованных СЭ, соответствующие сторонам G 1 G 2 , G 2 G 3 , G 1 G 3 ; R 1 , R 2 , R 3 – расстояния от центра СК УП до соответствующих СЭ; γ, ε, δ – углы в треугольниках G 1 OG 2 , G 2 OG 3 , G 1 OG 3 , противолежащие соответствующим сторонам a , b , с .

На основе уравнений связи (1) получается система из трех нелинейных уравнений с тремя неизвестными расстояниями до СЭ. Для решения этой системы уравнений необходимы величины расстояний a , b , с между СЭ , а также три косинуса углов при вершине O треугольников, образованных каждой парой из трех СЭ и центром СК УП [11].

Найденные косинусы углов и расстояния между СЭ подставляются в качестве исходных данных в систему нелинейных уравнений. Данная система уравнений решается численным методом, в данном случае методом Ньютона–Рафсона, который позволяет получать решения с любой степенью точности. Результа- том решения данной системы уравнений являлись расстояния от СК УП до СЭ [12] .

После определения искомых расстояний до соответствующих СЭ необходимо определить их декартовы координаты в СК УП, используя преобразования (2):

xi = Ri cos a i cos P i yi = Ri cos a i sin P i , zi = ^Ri ^{sin a} i

где α i , β i – угол места и азимут направления на i -й СЭ в СК УП; R i – расстояние от центра СК УП до i -го СЭ; x i , y i , z i – пространственные координаты i -го СЭ.

Если привязать к группе СЭ некоторую СК, то, вычислив декартовы координаты этих СЭ, можно однозначно определить линейное положение СК группы СЭ относительно СК УП. Для того, чтобы определить угловое положение СК группы СЭ относительно СК УП, необходимо определить матрицу направляющих косинусов ее осей.

Для определения матрицы направляющих косинусов необходимы следующие исходные данные:

– MТКЭ – массив теоретических декартовых координат СЭ, который состоит из пространственных координат в несмещенной (заранее определенной) СК группы СЭ относительно СК УП и имеет вид, представленный в (3);

– M ИКЭ – массив измеренных декартовых коор- динат СЭ, который определяется вычисленными по измерениям УП координатами в смещенной СК группы СЭ относительно СК УП и имеет вид, представленный в (4):

x Т 1

M ТКЭ =

x Т _ i

x И _1

M

ИКЭ

x И_ i

y Т_1    z Т_1

...         ...

yТ_i   zТ_i yИ_1   zИ_1

...          ...

y И_ i    z И_ i

где x _Т i , y _Т i , z _Т i – теоретические пространственные координаты i -го СЭ в СК УП; x _И i , y _И i , z _И i – измеренные пространственные координаты i -го СЭ в СК УП.

Используя данные массивы декартовых координат, однозначно вычисляется матрица направляющих косинусов, имеющая следующий вид:

	a ll	a 12	a 13
MNK =	a 21	a 22	a 23
	_ a 31	a 32	a 33 .

Угловое положение можно описать либо через последовательные повороты трёх углов Эйлера– Крылова, либо через кватернионы. Углы Эйлера– Крылова или кватернионы можно определить, используя найденные элементы матрицы направляющих косинусов (5) и выражения элементов одной из матриц (6), тем самым определяя угловое положение СК группы СЭ в СК УП. Выражения элементов матриц Т ^фЗ и T q соответствуют элементам матрицы MNK :

cos( ; ) cos( e )

T we = sin( ^ ) sin( ^Q ) cos( e ) - cos( ^ ) sin( ⁶ )

cos( y ) sin( ; ) cos( e ) + sin( y ) sin( e )

cos( ; )sin( e )                 - sin( ; )

sin( y ) sin( ; ) sin( e ) + cos( y ) cos( e ) sin( y ) cos( ; ) cos( y ) sin( ; ) sin( e ) - sin( y ) cos( e ) cos( y ) cos( ; )

q о + q i + q 2 + q 3

^T Q =

²⁽ q ₂ q i + q 3 q о )

²⁽ q 3 q i - q ₂ q о )

²⁽ q i q 2 ^- q 3 q о )

q 0 ^- q i + q 2 ^- q 3

²⁽ q 3 q 2 + q i q о )

²⁽ q i q 3 ^- q 2 q о )

²⁽ q 2 q 3 ^- q i q о )

q о ^- q i ^- q 2 + q 3

где T _ψφθ, T Q – представление матрицы направляющих косинусов (5) в углах Эйлера–Крылова и кватернионах; ψ, φ, θ – углы Эйлера-Крылова; q 0 , q 1 , q 2 , q 3 –

c =

n !

2 • ( n - 2)!,

кватернионы.

Для определения углов Эйлера–Крылова (ψ, φ, θ) или кватернионов ( q 0 , q 1 , q 2 , q 3 ) необходимо использовать выражения (7) и (8).

_t . ^T _vve [2,3]. ^v= ^arctg( T ^;;^ );

Ф = arcsm(^- T y^e [1^,3]);

о          Tv^e [i,2], e = arctg( ------); Tv,e [i,i]

5 = агссо8(о, 5 • ( T q [i,i] + T q [2,2] + T q [3,3] - 1 ));

q _о = cos( 5 );

q i =

T q [2,3] - T q [3,2] ^;

где С – количество уравнений; n – количество СЭ.

Заключение. Разработанный алгоритм позволяет определять линейное и угловое положение любых недеформируемых конструкций, используя только один УП, и может быть реализован на борту космического аппарата. В некоторых случаях, когда требования к точности определения положения достаточно грубые и существует возможность использования высокоточного оборудования для измерения углов, но при этом поверхность объекта имеет деформации в некотором известном диапазоне, то данная методика может быть применена после предварительной оценки максимальных погрешностей ее работоспособности.