Методика определения термического сопротивления многослойного пакета теплоизоляционных текстильных материалов в условиях обдува

Шарпар Н.М., Жмакин Л.И., Власов И.Н., Бокова Е.С. Методика определения термического сопротивления многослойного пакета теплоизоляционных текстильных материалов в условиях обдува. Нанотехнологии в строительстве. 2025;17(1):23–31. – EDN: URPYBE.

Волокнистые материалы и полотна технического назначения находят широкое применение в строительстве, промышленности и других отраслях экономики. Они могут быть изготовлены из различных материалов, таких как стекловолокно, базальтовое волокно, керамические волокна, минеральная вата и другие. Эти материалы, как правило, состоят из волокон микро и наноразмерного ряда, обладают высокой теплоизоляционной способностью, что позволяет использовать их для эффективной тепловой изоляции фасадов и других элементов зданий. В многослойных строительных конструкциях волокнистые материалы и полотна технического назначения [1–2] выполняют не только функцию теплоизоляции, но и защиты от влаги [3] и шума. Они могут быть применены как в качестве утеплителя для наружных стен и крыш, так и для внутренних перегородок и потолков. Кроме того, эти материалы могут быть использованы для создания систем вентилируемых фасадов, что позволяет улучшить теплозащитные свойства здания [4–5] и снизить энергопотребление на обогрев и кондиционирование воздуха. Волокнистые материалы и полотна технического назначения также широко используются в промышленности для теплоизоляции и звукоизоляции трубопроводов, аппаратов и оборудования. Они могут быть изготовлены с различной структурой и плотностью, что позволяет выбрать наиболее подходящий материал для конкретного применения. Таким образом, волокнистые матери- алы и полотна технического назначения являются важными элементами в строительстве и промышленности. Их высокие теплоизоляционные, звукоизоляционные и влагозащитные свойства делают их незаменимыми в создании комфортных условий жизни и работы в зданиях и сооружениях.

При проектировании и расчете многослойных строительных конструкций, таких как стены, кровли, потолки и другие элементы зданий, необходимо учитывать теплоизоляционные свойства каждого из слоев. Однако в реальности контакт между слоями имеет дискретный характер, что приводит к возникновению термических сопротивлений в зонах контактов отдельных слоев. Эти сопротивления могут значительно повлиять на теплопередачу [6–7] через конструкцию и, следовательно, на ее тепловую эффективность. Для учета контактных термических сопротивлений в зонах контактов отдельных слоев в многослойных конструкциях необходимо проводить теплотехнические расчеты с учетом термических свойств каждого слоя и тепловых потерь в зонах контакта между ними. Кроме того, необходимо учитывать такие факторы, как толщина каждого слоя, плотность материала, коэффициент теплопроводности [8–9], температурные градиенты и другие параметры [10–11]. Важно отметить, что контактные термические сопротивления могут иметь как положительный, так и отрицательный эффект на тепловую эффективность конструкции. Например, в некоторых случаях наличие контактных сопротивлений может уменьшить теплопотери через конструкцию и повысить ее эффективность [12]. В других случа-

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ ях наличие контактных сопротивлений может привести к ухудшению тепловой эффективности и повышенному потреблению энергии на обогрев или кондиционирование воздуха. В связи с этим учет контактных термических сопротивлений в зонах контактов отдельных слоев в многослойных строительных конструкциях является важным этапом при их проектировании и расчете. Это позволяет оптимизировать теплопередачу через конструкцию, повысить ее тепловую эффективность и снизить потребление энергии на отопление или кондиционирование воздуха.

Тепловой поток при подходе к контакту разделяется: одна часть идет через воздушный зазор, а другая через зоны фактического контакта между волокнами. Первое термическое сопротивление зависит от теплопроводности воздушной среды и величины зазора; поскольку в большинстве случаев конвекция в зазорах не развивается, то оно носит поверхностный характер. Второе же сопротивление имеет объемный характер. В тепловой цепи оба эти сопротивления включены параллельно, поэтому их обратные величины (иначе термические проводимости) суммируются. Особенно важен учет контактных сопротивлений при расчетах динамики температурных полей в многослойных ограждающих конструкциях [13–15].

Согласно феноменологической теории, понятие контактного термосопротивления является условным и не ограничивается только наличием границы раздела фаз. Контактное термосопротивление описывает явление, при котором внешняя плотность теплового потока вызывает появление разности потенциалов на границе раздела двух различных материалов. Однако контактное термосопротивление может проявляться не только на границе раздела фаз, но и внутри одной фазы при наличии микро- и наноструктурных дефектов. Эти дефекты могут быть вызваны различными факторами, такими как наличие дислокаций, примесей и других неоднородностей в кристаллической структуре. Контактное термосопротивление является важным параметром для понимания тепловых свойств материалов и может влиять на эффективность работы теплообменных устройств, таких как теплообменники и термоэлектрические устройства. Кроме того, контактное термосопротивление может быть использовано для измерения различных физических параметров материалов, таких как теплопроводность и температурные градиенты. Таким образом, понятие контактного термосопротивления имеет широкое применение в различных областях физики и материаловедения и не ограничивается только наличием границы раздела фаз. Его понимание и изучение является важным для развития новых технологий и улучшения существующих методов измерения физических параметров материалов, а на практике введение понятия температурного скачка на границе двух слоев имеет некоторые преимущества, т.к. его величина может быть легко определена экспериментально путем линейной экстраполяции температурного распределения в многослойном теле [13].

Наиболее просто контактное сопротивление находят в экспериментах по методу стационарного теплового потока, хотя в ряде случаев его можно оценить аналитически с помощью теоретического анализа модельных контактов [13, 14].

В целях снижения энергоемкости валового внутреннего продукта повысился интерес к рациональному потреблению тепловой энергии. Для этого в энергосберегающей программе [16] предусмотрено повышение теплозащитных характеристик внешних ограждающих конструкций [17, 18] общественных, жилых и промышленных зданий.

Подбор соответствующих теплоизоляционных покрытий [19] в качестве ограждающих конструкций осуществляют с учетом таких факторов, как температурно-влажностный режим окружающей среды, физические свойства текстильного материала, включая его влаго– и воздухопроницаемость, а также термическое сопротивление [20–22].

МАТЕРИАЛЫ И МЕТОДЫ

Ограждающие конструкции в виде пакета, состоящие из текстильных полотен, находятся под воздействием воздушного потока, направленного перпендикулярно поверхности обдува.

В работе представлены результаты исследования теплозащитных характеристик текстильных пакетов, обдуваемых потоком воздуха со скоростью, направленной по нормали к их поверхности.

На рис. 1 представлена схема, состоящая из n-го числа слоев текстильных полотен, находящихся под воздействием постоянного потока теплоносителя. В рассматриваемую модель входят следующие слои: первый – внутренний, расположенный у непроницаемой поверхности; последующий i -й и внешний n -й слой с окружающей средой – пакет материалов при x >  x_{n +1,1} . Слои пакета из текстильных полотен имеют толщины материала δ _{i 2} и воздушной прослойки δ _{i 1} ; вектор плотности теплового потока q на непроницаемой поверхности ( x = x ₁₁ +0) численно равен q в направлении оси x , скорость потока w воздуха, воздействующего на пакет; температуры на внутренней поверхности слоя, а также на поверхности текстильных полотен, находящихся внутри него и на поверхности самого пакета, обозначены, соответственно, t_{i 1} , t_{i 2} и t_{n+ 1,1} . Поток воздуха противоположно направлен к тепловому потоку. Скорость воздуха,

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

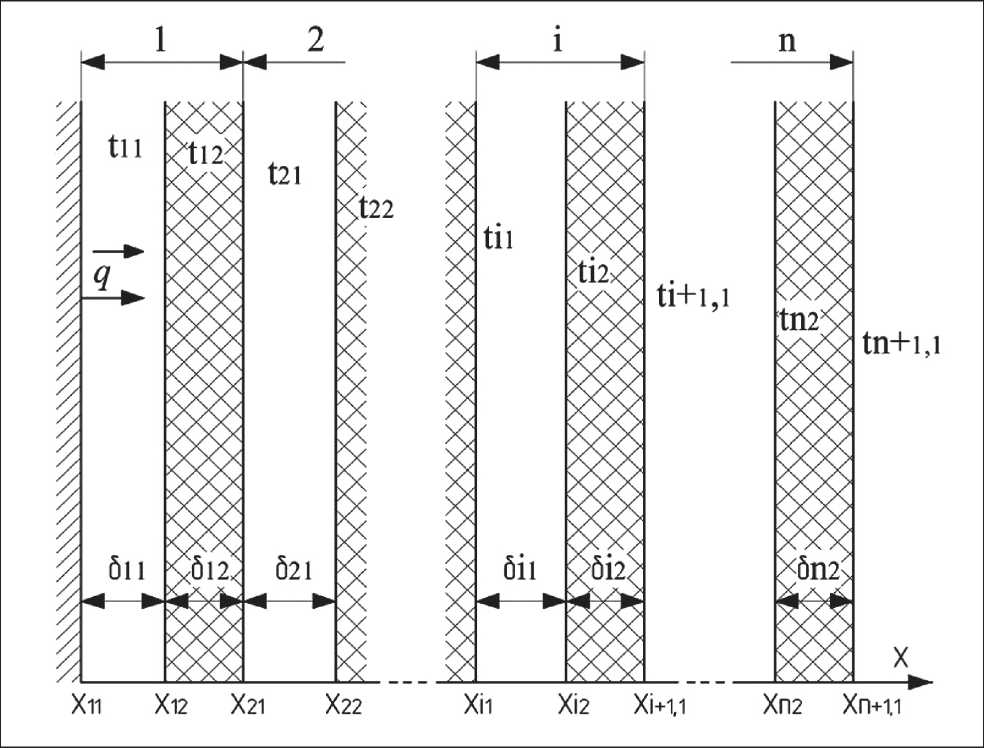
Рис. 1. Схема теплоизоляционных слоев пакета

прошедшего сквозь i-й слой, является заданной и постоянной внутри него [22]. Из-за незначительной толщины прослойки воздуха нормаль к поверхности компоненты скорости потока теплоносителя в зазоре представим рядом Тейлора wi(x) = wi–mi·(xi2–x), (1)

где m_i = ( w_i – w_{i –1} )/δ _{i 1} .

На рис. 2 приведен график скорости через слои текстильных полотен, образующих пакет.

С помощью граничных условий учитывается перенос тепла за счет излучения в воздушном зазоре между слоями материала. Согласно источнику [23], тепловой перенос определяется добавлением в уравнение энергии эффективного коэффициента теплопроводности, осуществляющего перенос тепла за счет теплопроводности воздуха в материале и радиации.

Тепловой поток, воздействующий на модель, рассматривается одномерным, согласно рис. 1, слева направо тепло переносится за счет излучения и теплопроводности, а справа налево только конвекцией. В условиях одномерной задачи, когда выполняются следующие условия w_x = – w , w_y = w_z = 0, d_t / d_x = f ( x ), d_t / d_y = d_t / d_z = 0 для i -й прослойки можно записать уравнение энергии в дифференциальной форме, которое примет следующий вид:

, tn(x\              z Xrdfii(x\

Л1 [----= -Ql • Al • wi (*)[—^] .(2)

dxzdx

Между i -м и ( i -1)-м слоями в пакете из текстильных полотен граничные условия соблюдают равенство тепловых потоков и температур на их границе:

ti1(xi1) = ti1,(3)

Xi=^^]xil+an^-^,(4)

где

,

.

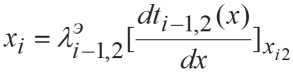
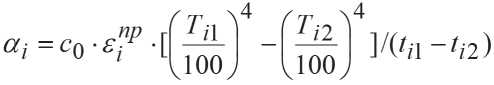
При рассмотрении границы между i -м и ( i -1)-го слоев, величина x_i является их кондуктивным потоком тепла, а α _i – коэффициент теплоотдачи – излучением между слоями рассматриваемого материала i -м и ( i -1)-м в плоской прослойке.

.

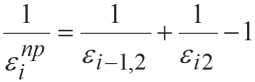
ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

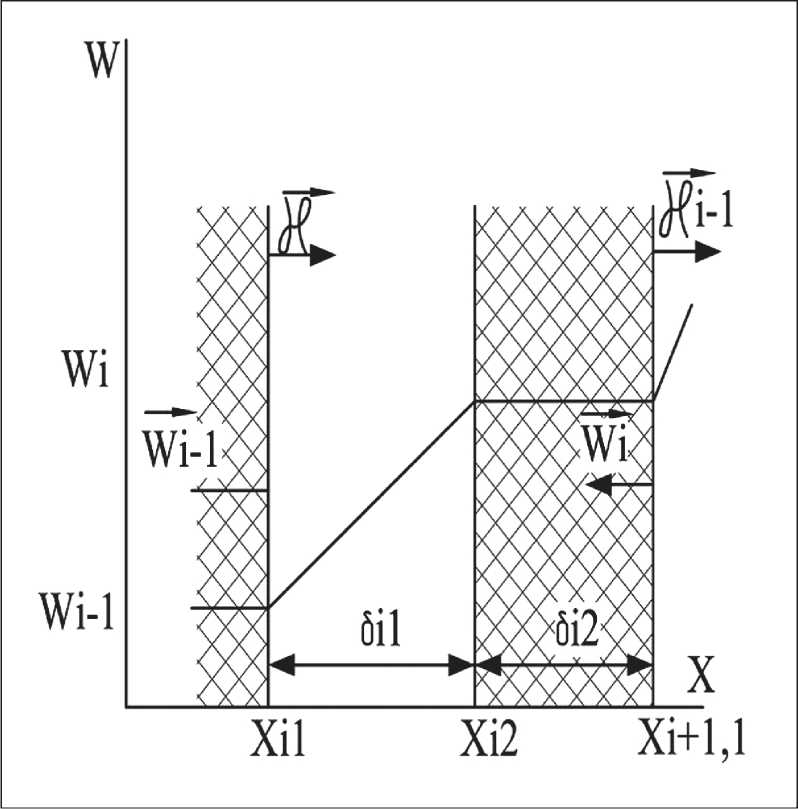
Рис. 2. График скорости через слои текстильных полотен, образующих пакет: w_i – скорость через i -й слой потока теплоносителя (воздух); w ( x ) – снижение скорости в i -м воздушном слое между полотнами текстильного материала i -го и ( i -1); – вектор плотности радиционно-кондуктивного потока, проходящий по внутренней поверхности i -го слоя пакета

Здесь ε _i ^np , ε _{i– 1,2} , ε _{i 2} обозначают приведенные степени поглощательной способности прослойки на границе между ( i -1)-м и i -м слоями рассматриваемого пакета из текстильных полотен; T_i – абсолютная температура, (°К).

Согласно вышеуказанным допущениям, дифференциальная форма уравнения энергии для i -го слоя материала будет аналогична форме уравнения пористого слоя [24]:

. (8) A2 ^

Между рассматриваемым материалом, находящимся в составе пакета и воздушной прослойкой i -го слоя, граничные условия характеризуют равенство потоков тепла и температур:

t_{i 2} ( x_{i 2} ) = t_{i 2} ,

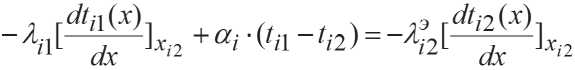
. (10)

Уравнения (2) и (8) относятся к линейным дифференциальным уравнениям 2-го порядка, но в последнем присутствуют постоянные коэффициенты, их решения можно представить в виде:

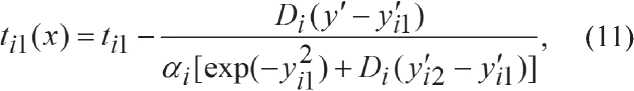
, . Z/^texpB^+A'fe^ WW? —;----о------

Лз^Я^рЬ'лН W/2 - Ул)]

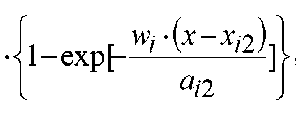
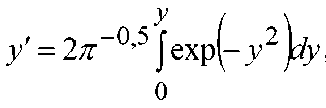
где D_i = [πα²/(2λ _{i 1} ·c _{i 1} ·ρ _{i 1} · m_i ]^0,5; переменная y = w_i ( x )/ J 2 mi • ац , причем между слоями yi 1 = w. _-1 /^2 mi • ац и У . 2 = w i / 4 2 mi • ац ; a i 1 — коэффициент температуропроводности в воздушной прослойке a_{i 1} = λ _{i 2} ^Э /(c _{i 1} ·ρ _{i 1} ); значения интеграла yʹ принимаются согласно [25]. Величина χ_{i +1} находится по рекуррентной формуле при условии, что χ_i = q :

exp^y^ + ACv^-yh)

Z/+1 = Xi --2-- expC-y^p + ^Cv^-y/l)

.                                      (14)

При помощи уравнений (11) и (12) можно определить температурный перепад ∆ t на границах воздушной прослойки или материала. Согласно формуле R = ∆ t / q термическое сопротивление можно представить в виде:

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

_Xi___ ^DM2-y'i^

q • ^i expf-j^ ) + Di (y’_j2 - у'ц )

Z/ + 1 = Xi •

i 2      2

1 Л’2 ^/1

И1Л2 ai2

+ —•

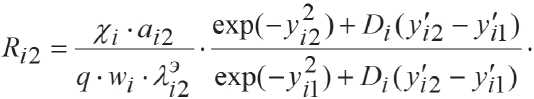
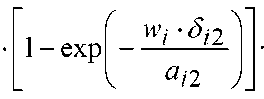
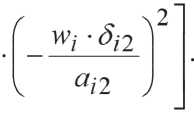
Термическое сопротивление теплоотдаче от наружной поверхности пакета из текстильных полотен к окружающей среде можно вычислить по формуле R_{n +1} = χ_{i +1} ·[ q (α _p + α _k )]^–1, откуда коэффициент теплоотдачи можно найти согласно уравнению (6) при замене T_{n +1,2} и t_{n +1,2} на температуры окружающей среды, а затем вместо ε _i ^np подставить степень поглощательной способности наружного материала ε _{n 2} , входящего в рассматриваемый пакет. Согласно формуле Г.Н. Кружилина [22], можно рассчитать коэффициент конвективной теплоотдачи для лобовой точки обдува:

Возможны два предельных перехода, первый осуществляется при w_i → 0. Тогда из уравнений (14)–(19) можно вывести следующие зависимости, описывающие теплопередачу во время отсутствия обдува:

Nu = 1,04·Re^0,5·Pr^0,33.

Термическое сопротивление всего пакета, со-

стоящего из текстильных полотен, определяется из суммы термических сопротивлений отдельных

материалов, входящих в его состав, воздушных про-

слоек и термического сопротивления теплоотдачи к окружающей среде.

Далее разберем предельные переходы в полученных формулах. В слоях, где скорости воздуха незначительны, т.е. когда y_{i 1} y_{i 2} < 0,02 и w_iδ_{i 2} / a_{i 2} < 0,1 , можно разложить выражения (14–16) в ряд, и тогда с ошибкой не более 1% в виде w_iδ_{i 2} / a_{i 2} < 0,1, после этого формулы (14), (15) и (16) упрощаются за счет разложения в ряд при ошибке не более 1%, тогда

χ i = q , R i 1 = 1/(α i + λ i 1 /δ i 1 ), R i 2 = δ i 2 /λ i 2 ^Э . (20)

Второй предельный переход происходит при высоких скоростях потока воздуха. При условии, что i -й материал, входящий в пакет, обладает высокой воздухопроницаемостью w_iδ_i / a_i > 5, согласно уравнению (14), можно записать χ_{i +1} = 0 с ошибкой не более 1%. Термические сопротивления ( i +1)-го слоя и последующих слоев с более высоким номером приобретают значение, равное нулю, а температуры в этих слоях приобретут тождественность температурам окружающей среды, что соответствует кривой 5 на рис. 3. При таких условиях теплозащитные механизмы материалов сводятся к ветрозащитным, и поэтому становится ясной целесообразность использования ветрозащитного слоя. Таким примером могут служить строительные конструкции. Использование в защите слоя с низкой воздухопроницаемостью способствует эффективному выполнению теплозащитных функций другими слоями пакета.

уравнение для расчета соответствующего термиче-

ского сопротивления примет вид:

D Xi 1-^Уи(У/2~Уи)

q / + l1-2hi(fe-y;i)l ^71

Xi • ^/2 t¹ - Уд ~ Уп )⁺ I¹ ~ ²^'l ^/2 - Л1)] q-X-₂      1 + [1-²Ж(Л2-Л1)]

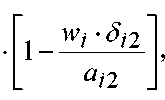
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Для применения расчета термических сопротивлений к строительным объектам следует определить воздухопроницаемость отдельных слоев [26, 27], входящих в состав пакета в условиях воздействия потока окружающей среды, а также определить закономерности изменения толщины воздушных прослоек. Поскольку эти величины неизвестны, ограничимся зависимостями воздухопроницаемости от теплозащитных свойств теплоизоляционного пакета. Для решения поставленной задачи воспользуемся предположением о том, что скорость потока среды в i -й прослойке пропорциональна ее воздухопроницаемости и динамическому напору воздушного потока среды, задержанного материалом в пакете:

w_i = b_hi ·ρ _i ( w_{i +1} ² – w_i ²)/2 h_i ,

ТЕХНОЛОГИИ ПРОИЗВОДСТВА СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ

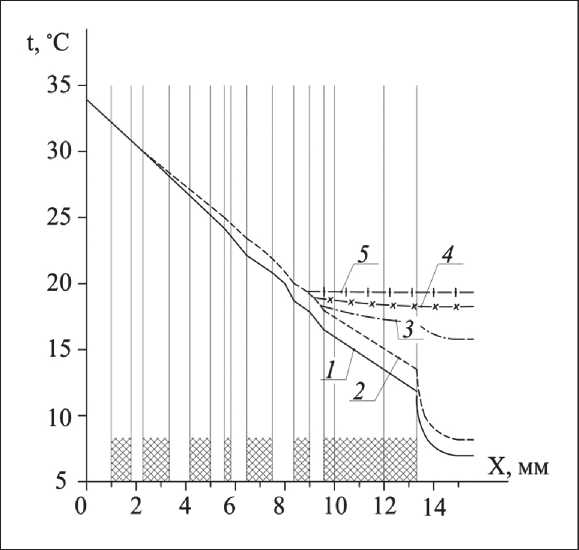
Рис. 3. Схема расположения температурных кривых, полученных расчетным путем: 1 – w _∞ = 0, a_i = 0; 2 – w _∞ = 0, a_i ≠ 0;

3 – w _∞ = 4 м/с, a_i ≠ 0; 4 – w _∞ = 10 м/с, a_i ≠ 0;

• 5 – w _∞ = 20 м/с, a_i ≠ 0

  где h_i – перепад давления, который определялся при воздухопроницаемости b_hi .

  Подобная формула использовалась П.А. Колесниковым [28], но изменение толщины прослоек во время расчетов учтено не было. На рис. 3 приведена схема расположения температурных кривых за ее пределами, они показаны условно. При расчете использовали метод последовательных приближений. За исходное распределение температур были приняты температурные кривые при условии, когда воздух считался неподвижным, а теплообмен за счет излучения в воздушной прослойке отсутствовал.

  Согласно схеме на рис. 3, на снижение термического сопротивления пакета влияет рост скорости обдува. По ходу кривых можно проследить оба описанных ранее предельных случая. Как видно из схемы, во внутренних слоях исследуемого пакета температурные кривые практически совпадают, это явление прослеживается из-за малой скорости воздушного потока. Также кривая 5 свидетельствует о том, что с увеличением скорости обдува падает

  
  

  термическое сопротивление на наружной поверхности пакета.

  ЗАКЛЮЧЕНИЕ

  – В работе рассмотрен нестандартный подход, и приведены уравнения для расчета термических сопротивлений как отдельных слоев, так и теплоизоляционного пакета в целом, в условиях обдува потоком воздуха лобовой точки.

  – Установлено, что при реальных испытаниях теплозащитного пакета толщина воздушных прослоек будет снижаться, а проникновение холодного потока в материал будет значительно глубже.

  – Показано, что рассмотренный подход более достоверно отражает основные закономерности теплопередачи через теплозащитный пакет в условиях обдува окружающей средой, тем самым приводя усложненное решение задачи к более простому изучению воздухопроницаемости и деформации слоев пакета.