Методика определения требуемых значений характеристик системы цифровой обработки данных дистанционного зондирования Земли

Система цифровой обработки (далее – СЦО) данных дистанционного зондирования Земля (далее – ДЗЗ) является сложной вычислительной системой, качество функционирования которой зависит от многих параметров (атрибутов). Получение результирующей оценки качества по многим параметрам является сложной математической задачей принятия решения по нескольким критериям. Целью данной статьи является разработка математического обеспечения оценивания качества системы цифровой обработки данных ДЗЗ, которое включает в изложенном ракурсе рассмотрения модель системы и методику оценивания гарантированного значения показателя качества ее функционирования.

Агрегированная математическая модель системы цифровой обработки

Агрегированная математическая модель системы цифровой обработки данных включает в себя две составляющие – модель вычислительной системы и модель условий ее применения [1].

Приступая к математическому моделированию СЦО, необходимо определить три группы спецификаций:

• •    атрибуты процесса функционирования, определяющие качество результата;

• •    атрибуты системы, влияющие на качество ее функционирования;

• •    характеристики условий функционирования системы.

Целевой эффект функционирования вычислительной системы в общем смысле определяется расходом ресурсов R по трем составляющим: техническим, энергетическим и технологическим:

R = С , E , Teh .                                        (1)

Будем считать, что в наземном комплексе обработки возможно обеспечить любой объем энергетической составляющей, таким образом, R = С , Teh . Вектор атрибутов, характеризующих качество функционирования СЦО, включает целевой эффект функционирования вычислительной системы V = V ( R ) и затраты операционного времени на обработку полного объема поступивших данных т :

Методика определения требуемых значений характеристик системы цифровой обработки ...

Y = V , т .                                         (2)

Атрибутами системы являются ее эксплуатационно-технические характеристики, проектные параметры, а также характеристики процесса функционирования, влияющие на качество функционирования [10]. Для вычислительных систем, к которым относится и система цифровой обработки данных ДЗЗ [11], эксплуатационно-техническими характеристиками являются: производительность узлов обработки П _у , пропускная способность каналов информационного обмена с окружением c_k , пропускная способность каналов внутреннего информационного обмена C _no и объем оперативной памяти V _{o n} . Для процесса функционирования СЦО атрибутами являются количество операций K _on , требуемых для обработки всего поступившего объема данных [12], и количество потоков параллельной обработки N _nom , на которое можно разделить процесс. Таким образом, вектор управляемых атрибутов системы А ‘ , влияющих на качество ее функционирования, выглядит следующим образом:

^А = K on , N nom , V o . n , ^Пу , C u . o , ck ^{.                        (3.1)}

К дополнительным проектным параметрам системы, оказывающим влияние на длительность ее функционирования [13], относятся: разрядность вычислений r , основание алгоритмов обработки радиолокационных сигналов f , топология взаимосвязей узлов обработки S и протокол передачи данных по каналам информационного обмена Pr . Исходя из этого вектор неуправляемых (в рамках текущего исследования) атрибутов А " системы имеет вид

А" = r , f , S , Pr .                                          (3.2)

Полный вектор атрибутов можно представить как

А = А', А" .                                        (4)

Характеристики условий функционирования СЦО составляют вектор B' . К ним относятся параметры, с которыми запускается выполнение целевой функции обработки: длительность зондирующего импульса t_imp ,частота дискретизации F_d , период повторения зондирующего импульса T_pi ,длительность зондирования t _c , длина волны X, ширина спектра сигнала F_sp , высота орбиты H , реализуемое и требуемое разрешение resol по дальности и азимуту [14]. Все указанные параметры должны быть учтены при обработке поступающих радиолокационных данных [15]. Таким образом, вектор характеристик условий функционирования выглядит следующим образом:

B ' = t imp , F d , T pi , t c , ^A , F sp , H , resol .                                 (5)

Далее необходимо определить связь трех групп спецификаций из шага 1: зависимость параметров функционирования системы (2) от параметров самой системы (3), (4) и условий функционирования (5), а также от организации процесса функционирования [16], которая выражается в виде плана задействования системы Plan при известном информационном потоке.

Подставляя (1) в (2), получим вектор характеристик функционирования системы:

Y = V ( C , Tec ) , T .

Зафиксируем техническую структуру C и технологические возможности Tec как неизменяемый набор характеристик. Варьируемым параметром оставим операционное время т . Получаем зависимость для управляемых атрибутов А' :

-^/- / П_у

N 7

пот

— ^т V >2V  .

о . п      ргг

C . . 0 >П обр

с . > П обр

С учетом неуправляемых атрибутов А " зависимость выглядит следующим образом:

K ^{0n (} f ) / и / пот

( П ( r ) , S ,Pr ) = t_{v >w} . \ 7^х'       )     оп . п^^ргг

С«.о >Побр с. > Побр

Условия функционирования системы B' определяют априорный объем поступающих данных, количество потоков, на которые может быть распараллелена обработка, и количество операций на поток, которое потребуется для обработки данных. С учетом этих условий зависимость (8) трансформируется в зависимость (принимаем для расчета объ- ема поступивших данных Vpгг, что запись ведется в к квадратурах, поляризация kp - полная, разрядность АЦП ra, разрешение resolпо азимуту и дальности одинаковое)

T pi

Vp= г = kk r F-----1 ; рос pa          e

T emp

T pi

N _ пот

= N -от ⁽ resol ^{) =} F l”--- t e / resol ;

^Т етр

^{К оп (} f , ^V pгг ) / _П ^N поm ( resol )     ^о6р

( П _у ( r ) , S ,Pr )

.

^V оп > 2 Vp c

С ио >П обр

С . >  ^Побр

После определения зависимостей всех спецификаций друг от друга определяется математическая модель целевого функционирования СЦО. Она включает в себя реализуемый функционал системы со всеми его параметрами (агрегатами) и закон распределения показателя качества процесса функционирования.

Целевое функционирование СЦО есть выполнение технологической цепочки обработки поступающих данных ДЗЗ. Она основывается на синтезировании радиолокационного изображения (далее – РЛИ).

Алгоритм синтеза радиолокационного изображения [2] в математическом эквиваленте имеет следующий вид:

– вычисление опорных функций по дальности f , азимуту g ;

- вычисление спектра зарегистрированного сигнала UI(r",x") и опорной функции по дальности f по числу импульсов: Fr

–

вычисление Фурье-образа

[ U r ( r " ,x ") ! , F r [ f ] ;

(БПФ) функции свертки по дальности

F r [ h ] = F r [ U > ( r ", x' ' ) ] F r [ f ] ;

– вычисление функции свертки по дальности h = Fr-1 [Fr [h]] ;

Методика определения требуемых значений характеристик системы цифровой обработки ...

• -    вычисление спектра функции свертки по дальности по числу отсчетов F x [ h ] , F x [ g ] ;

• -    вычисление БПФ функции свертки по азимуту F x [ U ( r ', x ' ) ] = F x [ h ] ■ F x [ g ] ;

  - вычисление функции свертки по азимуту для получения итогового РЛИ U ( r ', x ‘ ) :

U ( r ' , x ' ) = F x ^{- 1} [ F x [ U ( r ' , x ' ) ]] .

Исходя из приведенного алгоритма математический эквивалент синтеза РЛИ можно представить как

U ( r ‘ , x ' ) = F x - 1 [ F x [ F r - 1 [ F r [ U ( r ", x ") ] F r [ f ] ]] F x [ g ] ] -                    (10)

При этом обработка может быть выполнена как на одном узле, так и на нескольких с распараллеливанием либо по данным [3], либо по участкам алгоритма.

Агрегаты функциональных элементов представляют собой функции, объединяющие их техническую и технологическую структуру [6], набор значимых характеристик (атрибутов) (4), набор условий функционирования (5) и набор условий применения. Набор условий применения B " представляет собой план задействования ресурсов Plan , построенный на основе информации [7] о периодичности поступления входных потоков. В случае нестационарного информационного потока (11) набор условий применения имеет вид

Pm (tо,t) = —e-a- = 0,1,-.n .(11)

m !

B" = B"(Plan(P- )) .(12)

Таким образом, агрегат [1] функционального элемента системы a = a( C, Tec; A, B', B").(13)

Модель целевого функционирования системы [8] также содержит описание закона распределения показателя качества Y ( 6 ) . В общем виде он может быть описан выражением

Фр -(V,т) = P[(9> V)о(?<т)] .(14)

В завершение моделирования вычислительной системы разрабатывается блок управления качеством СЦО и ее функционирования, который представляет собой подвектор управляемых компонент (16) вектора атрибутов системы (15) и способы управления ими:

X = A, B ‘;(15)

U = A', BVX X .(16)

К способам управления компонентами вектора U относятся стратегии их изменения для достижения требуемого результата [9]. При этом из компонент вектора B' управляемым компонентом является только выходное разрешение РЛИ resol , которое может быть изменяемо по правилу: если время обработки данных превышает предельно допустимое, ухудшаем разрешение, что приведет к снижению количества параллельных потоков обработки и количества операций на поток, то есть к снижению операционного времени обработки.

Затем начинается описание второй части агрегированной модели СЦО – модели условий ее применения. Первыми учитываются требуемые значения показателя качества целевого функционирования.

Требуемое значение показателя качества описывается вектором Z :

7 = V т ^   * m ^,Tm ^.

Здесь V _m - необходимые ресурсы и технологии для выполнения целевой функции; т _т - требуемое потребителем информации ограничение на время выполнения целевой функции.

После этого определяется связь требований к качеству функционирования системы и условий ее функционирования. Условие функционирования приведено в виде формулы (11) и характеризует входной поток данных как нестационарный пуассоновский. Исходя из этого определим закон распределения промежутка времени T между наступлениями соседних событий [3].

Пусть первое событие появилось в момент времени t ₀ . При этом условии закон распределения времени T между этим событием и последующим находится следующим образом:

F t _o ( t ) = PT <  t = 1 - PT >  t . (18)

PT >  t - вероятность того, что на участке от t 0 до t 0 + t не появится ни одного события:

1 0 + t

- J Я ( t ) dt

PT >  t = e - a = e ‘ ⁰

Подставляя (21) в (20), получим

t 0 ⁺ t

- j Я ( t ) dt

F t o ( t ) = ¹ — e t 0

Дифференцируя (20), найдем плотность распределения потоков:

1 0 ⁺ t

- J Я ( t ) dt fto ( t ) = 4 t 0 ⁺ t ) e t ⁰

t >  0 .

В формулах (11), (18)–(21) использованы обозначения:

a - математическое ожидание числа событий на участке от t ₀ до t ₀ + t ,

Л ( t ) - мгновенная плотность потока, 2 ( t ) = lim

Д t ^ 0

m ( t + Д t ) - m ( t ) Д t

t 0 + t a = J Л(t)dt;

t ₀

Знание этих законов позволяет определить количество требуемых параллельно функционирующих вычислительных ресурсов обработки N :

V = V ( C , Tec )

V = V ( NC , Tec )

r < T т >  T .

Таким образом, искомая связь требований к качеству и условий функционирования СЦО определяется системой (22) и выражением

N = —

T

.

Методика определения требуемых значений характеристик системы цифровой обработки ...

Далее определяется подвектор управляемых компонент вектора характеристик условий применения СЦО B" и способы управления ими [1]. Таким образом, с учетом шага 4 моделируется способ управления требуемым качеством целевого функционирования системы.

С учетом рассматриваемых условий поступления входного потока вектор B " пуст. Следовательно, управление требуемым качеством функционирования СЦО ограничивается описанным в шаге 4(уравнение (16)).

В конце определяются соотношения между компонентами векторов – определяющего качество результата целевого функционирования Y и определяющего требования к качеству Z :

V > V m ; т < т_т .                                 (24)

В полученной при выполнении данного алгоритма агрегированной математической модели СЦО приведена взаимосвязь управляемых компонент вектора А' (3.1) и показателя качества ее целевого функционирования (6).

Методика оценивания качества функционирования системы цифровой обработки дистанционного зондирования Земли

Шаг 1. Формулирование критерия оценивания качества результата целевого функционирования:

G ^P : Y е { Z } = U -                                   (25)

Шаг 2. Вычисление показателя эффективности функционирования системы в виде вероятности достижения ее цели:

Р _йц = P ( Y ^ { Z } ) -                                 (26)

Шаг 3. Определение требований к эффективности функционирования (минимально допустимое значение вероятности достижения цели) р т .

Шаг 4. Формулирование и реализация критерия пригодности системы по степени достижения целевого эффекта:

^G ц₃ : ^р _йц > ^.                              (27)

Шаг 5. Непосредственное оценивание эффективности функционирования СЦО по формулам (25)–(27).

Выполнение пятого шага приведенной методики в указанной общей формулировке подразумевает под собой выполнение нескольких действий:

• 1.    Формирование n -мерной области допустимых значений управляемых атрибутов системы, при которых гарантированно удовлетворяется условие Р _йц >  Р тЦ^ -

• 2.    Вычисление каждого из n значений управляемых атрибутов оцениваемой системы.

• 3.    Построение нормированной точки в n -мерном пространстве и анализа ее положения.

Сформируем область допустимых значений управляемых атрибутов системы

^А = K on , N nom , V o . п , ^ у , C u . о , C K ^-

В общем виде синтез РЛИ состоит из четырех преобразований Фурье (далее – БПФ) и двух сверток радиоголограммы с опорами [2].

Количество операций K _on зависит от объема потока, выраженного в количестве отсчетов N (рассчитывается от объема радиоголограммы) и алгоритма обработки:

VT

W =    = kk p F_d-’ p- t _c .                              (28)

' а               стр

Математическая сложность БПФ по основанию 2 составляет     log₂ N операций [5].

Следовательно, общее количество операций рассчитывается в рассматриваемом случае как

3 N

K on 2 = 2 W + 4—log 2 W = 2 W + 6 W log 2 W .

Отношение количества операций к объему обрабатываемых данных при одном потоке обработки составляет производительность алгоритма:

K on = 2 W + 6 W log₂ W

N

N

= 2 + 6 log 2 W .

При возможности организации распараллеливания обработки по данным значимым параметром является удельная сложность алгоритма на потоке, которая определяется соотношением

K on

N пот

.

Количество потоков параллельной по данным обработки при этом определяется требуемым разрешением итогового радиолокационного изображения.

Полученная удельная сложность алгоритма (31) является значимой характеристикой только во взаимосвязи с производительностью вычислительного устройства Пу, при этом наиболее удобной в данном случае мерой производительности устройства является MIPS. Чем меньше соотношение to6p

оп

N / ^у , пот

тем выше производительность аппаратно-программного вычислительного комплекса. Именно формула (32) определяет время обработки поступающих данных при условии поступления данных по каналам внешнего информационного обмена без очередей, достаточных объема оперативной памяти и пропускной способности каналов внутреннего обмена.

При наличии i узлов параллельной обработки и i ( i - 1 ) /2 каналов внутреннего информационного обмена (то есть при наличии полносвязной сети) выражение (32) приобретает вид

* о.р = 2^ / П „ + 2 j                (33)

i ^{W nom i}             i ( i — 1 ) /2 C ij

С учетом задержки на прием и передачу данных по каналу внешнего информационного обмена

VVV

U = "7+ + 2^" " ^ / Пi + 2 7 j +^ ^^ .             (34)

ck      i ^W nomi           i ( i - 1 ) /2 C uoij      ck

Исходя из приведенных соотношений (28)-(34) и ограничения t _o6p < T_{l m} получаем логичные граничные значения для формирования области допустимых значений:

Методика определения требуемых значений характеристик системы цифровой обработки ...

TT  T

K o„ <  2 kk p F d -^-te + 6 kk p F d -^-t e log 2 kk p F d -p- t e ;

T emp              T emp               T emp

T pi

N nom <  F d”--- t e / resol ;

T emp

П >

T pi

² + 6log 2 kk p F d---- t e

T emp

T ;

Fd----te / resol

T emp

C

c uo

T pi

² + 6log 2 kk p F d--- t e

T emp

≥ _T

F d  —t _e / resol

T emp

^T pi

² + 6log 2 kk p F d--- t e

T emp

≥        Tpi i ■ Fd------te / resol

T emp

T

V o„ >  2 kU d      !.Г а .

T emp

;

;

Видно, что четыре из шести вводимых атрибутов системы зависят от количества опе-

раций K _on . При этом само количество операций, которые могут быть выполнены за отведенное время, ограничивается удельной производительностью аппаратной части и количеством потоков распараллеливания данных, зависящих от их объема. Пользуясь эффектом поглощения [1], можно упростить векторный показатель качества, свернув первые три его составляющие в атрибут удельной производительности аппаратно-программного устройства [4]:

№ ^п; > T r ".

T lim

Пропускная способность каналов внешнего информационного обмена должна быть не менее, чем эта же характеристика П _у , выраженная в объеме данных, обрабатываемых в единицу времени для входного узла. Пропускная способность каналов внутреннего информационного обмена должна превышать производительность узла, следующего за работающим, также выраженную в объеме информации, обрабатываемой в единицу времени.

Исходное пространство допустимых значений принимает вид, представленный на Рисунке 1.

Допустимыми значениями, исходя из условий задачи, являются значения, находящиеся вне синей черты. Применение разработанного математического обеспечения позволяет провести моделирование системы цифровой обработки данных и оценить качество ее целевого функционирования по управляемым атрибутам, что соответствует достижению цели исследования.

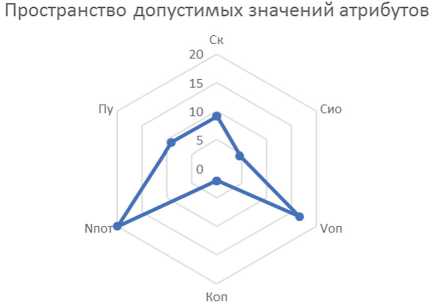
Рисунок 1. Пространство допустимых значений атрибутов системы

Заключение

Рассматривается оценивание качества системы цифровой обработки данных ДЗЗ при использовании параллельной по данным обработки. При использовании параллелизмами участков алгоритмов оценка количества операций будет более сложной. Однако изменение формулы не вносит изменений в саму суть методики, поэтому она может быть насыщена дополнительными оценками. К примеру, регулировка значений, которые представлены в виде вектора A ′′ неуправляемых характеристик, имеет огромную значимость при практическом проектировании и реализации системы цифровой обработки. Разработка методики выбора дополнительных проектных параметров системы является направлением дальнейших исследований.