Методика оптимального выбора конструктивных параметров специальных оптических разъемов для датчиковой аппаратуры

Мультисенсорные преобразователи бинарной информации (МСПИ) находят все большее применение в системах управления (СУ) сложными техническими объектами в робототехнике, станкостроении, авиастроении и других отраслях науки и промышленности [1]. Одними из наиболее ответственных элементов МСПИ, определяющими общий энергетический баланс их волоконно-оптической схемы, являются оптические разъемные соединители (РОС). Стандартные РОС, серийно выпускаемые отечественными и зарубежными производителями [2] для оптических систем связи, состоят из оптической розетки и двух наконечников с установленными в них передающими приемными световодами. Наконечники присоединяются к розетке с помощью резьбового, байонетного или иных типов креплений. Такие РОС обладают низкими энергопотерями, однако их габариты не всегда отвечают требованиям их конструктивной интеграции с малогабаритной датчиковой аппаратурой. В связи с этим возникает задача создания методов оптимального проектирования параметров специализированных малогабаритных РОС с учетом заданного уровня энергопотерь.

ПОСТАНОВКА ЗАДАЧИ

В качестве критерия оптимизации чаще всего используется минимум стоимостного функ-

ционала, отображающего зависимость суммарных затрат C ^ на изготовление РОС с учетом зависимостей стоимости изготовления C_i от значения конструктивного параметра x_i [3]. Типовая зависимость C_i ( x_i ) имеет вид:

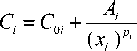
где C 0 i , A i , p i - параметры аппроксимирующей функции.

Графическая иллюстрация этой зависимости приведена на рис. 1,а.

С другой стороны энергетические потери B_i , вносимые i –тым фактором, также зависят от x _i :

B(x^ = 10lg[F(x, b^.bk)], где xi,b1,...,bk - параметры аппроксимирующей функции, причем:

F (Xi, bv..bk) x,_0 = Bо, где B0 - составляющая общих потерь, независящая от точности изготовления РОС, например, потери ввода излучения от источника в центральный световод оптического демультиплексора с использованием стандартного оптического разъема, погонные потери, определяемые длиной световода, которая задана в техническом задании на изготовление МСПИ и ряд других.

Типовая зависимость B ( x i ) приведена на рис. 1,б. Как видно из рис. 1,а и 1,б, зависимости C i ( x i ) и B ( x i ) описывают взаимно противоречивые тенденции: увеличение аргумента этих функций приводит к уменьшению стоимости изготовления и увеличению энергетических потерь и наоборот.

Таким образом, задача оптимизации сводится к отысканию таких значений x _i , при которых обеспечивается компромисс между стоимостью изготовления устройства и потерями, вносимы-

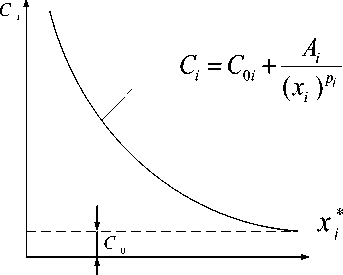
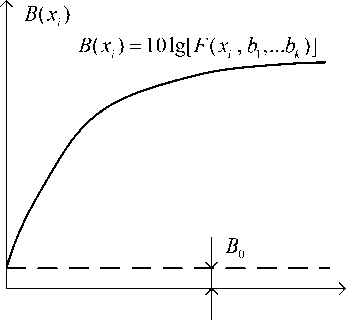
а)                                                                   б)

Рис. 1. Типовые зависимости C i. ( x i ) и B ( x,)

ми отдельными конструктивными факторами.

В общем случае суммарные энергопотери определяются большим числом факторов, поэтому расчет оптимальных значений влияющих факторов сводится к поиску условного экстремума функции многих переменных x _i . Как видно их приведенных графиков, функции C_i ( x_i ) и B ( x i ) непрерывны вместе со своими частными производными в диапазоне изменения аргумента, что позволяет использовать для решения оптимизационной задачи метод множителей Лагранжа [4].

РЕШЕНИЕ

Рассмотрим методику расчета оптимальных значений x _i , предусматривающую обеспечение требуемого значения B_доп при минимальном значении стоимости изготовления Ф . Для этого запишем минимизируемую функцию в виде:

(             A n

Ф = Ц ^С о . + -Aip- I + Ц А ( a .' X — В _й„ )|,   (1)

г = 1 V        V xi ⁾ ) V г = 1                        )

где A i - множители Лагранжа, устанавливающие связь между стоимостью изготовления элемента и вносимыми им энергопотерями, У • е.

[ Xi . ^ = ~ОБ ’ Вдоп — заданное допустимое значение суммарных потерь.

Как известно, для последовательной схемы включения оптических элементов МПИ суммарные энергетические потери равны сумме потерь от влияния отдельных факторов:

m в = = Z B , = 1

где B _i – энергетические потери, вносимые i -тым фактором, m – число таких факторов.

Следует отметить, что точное нахождение экстремума функционала (1) требует знания конкретных параметров входящих в него выражений для стоимости C_i ( x_i ) и энергопотерь

B ( x i ), которые можно получить, например, экспериментально. Однако в этом случае значения этих параметров для конкретных элементов в значительной степени зависят от применяемого технологического, контрольно-измерительного оборудования и материалов, что приводит к существенному разбросу параметров зависимостей C i ( x i ) и B ( x i ). К такому же эффекту приводит неточность рекомендуемых различными авторами математических формул для расчета энегопотерь, полученных с определенными допущениями и ограничениями [4]. Поэтому точное решение задачи оптимизации представляется малореальным.

Однако для случая малых отклонений оптико-механических параметров элементов x _i от номинальных (нулевых) значений, таких как осевые, боковые, радиальные зазоры, несоответствие диаметров, апертур световодов в соединениях и др., справедливо ввести следующие допущения:

mm р, = -1 ZPi= 1; 4,=-Za.;

m i           m V

m

C„ = - Z C Oi .        (2)

m о

Полученные с учетом введенных допущений значения x _i , строго говоря, являются квазиоп-тимальными. Однако принятые допущения, с одной стороны, позволяют существенно упростить решение задачи, а с другой – корректно применить полученные результаты для ряда практически важных частных случаев [5].

С учетом принятых допущений стоимостной функционал (1) можно представить в виде:

m^ (     A_ A m ф - Zkc +    I + ^=P |Z a-' x.-ВЙОД. (3)

i = 1 V          xi )        V i = 1                   )

Уравнение связи представим в виде: mm

,

L / A I I / A i don ’ i = 1                  1

дB.

где a. = —^L - коэффициент влияния i -го фак- 5 х₍

ПРИМЕР ОПТИМАЛЬНОГО РАСЧЕТА КОНСТРУКТИВНЫХ ПАРАМЕТРОВ РОС

тора на суммарные энергопотери.

Находя частные производные функционала (3) по переменным x _i и приравнивая их к нулю, получим с учетом p_ср = 1 систему уравнений:

d Ф = d х ,	- Ae + х ,	2 ср a , =	0
d Ф = d х i	- A^+ х i	2 ср a i =	0	'■	(5)
d Ф _ d х m	_ AJPL-l X m 2	2 ср a m	= 0 .

Пусть в каждом оптическом канале МПИ содержится n одинаковых последовательно включенных РОС. Доминирующими источниками энергетических потерь в них являются осевое смещение h , радиальное смещение l , угловое смещение 0 осей световодов (см. рис. 2). Оптические потери каждого РОС равны:

B op = B h + B i + B 0 ,

Из первого уравнения системы (5) находим:

2. =   A ^cp   .

^ср a , • x ,²

Из второго уравнения системы (5) получим:

AA ср __ ср г = г. aixi    a, x

где B_h – потери за счет осевого смещения, B _l – потери за счет радиального смещения, B ₀ - потери за счет углового смещения. Тогда для случая последовательного соединения n разъемов: B l = n ■ ( B h + B i + B 0 ) .

Пусть n = 3, допустимое значение суммарных энергопотерь для трех разъемов Bd0nz =, дБ , B причем, Bh = Bl = BQ = доиz . Тогда, применяя формулу (11), полагая что a, = ah, получим:

Приравняем выражения (7) и (6):

aixi

x hOnT

B ^0„

n

Тогда:

Откуда:

x = xi a1

. a

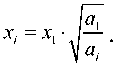
С учетом уравнения связи (4) можно записать: nnn x1a1

B_y = } a. ■ x. = ) —.     ■ a. = x ч/ a. ■ >  Ja.

L                                                               Z 1          1

= 1                Z = 1        azZ

Откуда x, S----BOt----.(10)

a^ • E Ta i=1

Подставляя (10) в (9) получаем расчетную формулу:

x , S---- B 0r ----.          (11)

T a" • E a^

i = ,

Для проверки правильности полученной формулы осуществим проверку c использованием уравнения связи (4):

Bz = t-. ■ x„, S B,_ • E----1----= B,_ • E -AA- = i ■'                  i='Va7-E Va7         i='E Va7

i = ,                                        i = ,

+                          + ...

T a , + Т ^ Г + ... + V a 7 T^ + T " ? + ...+ Т О Г    T^ + 7 ^ 7 +... + 7 " П

T a ! +7 a 7 + ... +T a n = ,

7 " ? ⁺ 7 " ? ⁺ ... ⁺ 7 " П

Inl-^¹- = ‘^ v

= ^Bd0n

Следовательно, методика верна.

i = !

B h

.

³ a h

Аналогично:

Bi-B^

Х1ОПТ        ’ x0опт.

3 al3

Вычислим значения x _honT , х _1опт , x _{0 опт} , если диаметр волокна d = 50 мкм , а относительный показатель преломления А = 0,01. Результаты вычислений представлены в табл. 1.

В рассмотренном примере выражение (11) используется для расчета однотипных потерь, что соответствует введенным выше допущениям (2). Таким образом, используя вышеприведенную методику расчета, можно определить оптимальные конструктивные параметры оптической схемы, при которых уровень потерь не превышает допустимого. Указанная методика может быть использована также и для других видов потерь (например, из-за рассогласования числовой апертуры, или изгибов волокна) [1, 6].

ЗАКЛЮЧЕНИЕ

Представлена методика оптимального выбора конструктивных параметров МПИ и их отклонений от номинальных значений по минимуму функции стоимости изготовления. Указанная методика учитывает различия зависимости стоимости от точности изготовления механических и электронных элементов МСПИ и позволяет избежать неоправданных энергетических потерь и экономических затрат. Данная методика позволяет выбрать оптимальные конструктивные параметры, не прибегая к дорогостоящим экспериментам. Отметим, что достоверность результатов расчета зависит от корректности аналитических

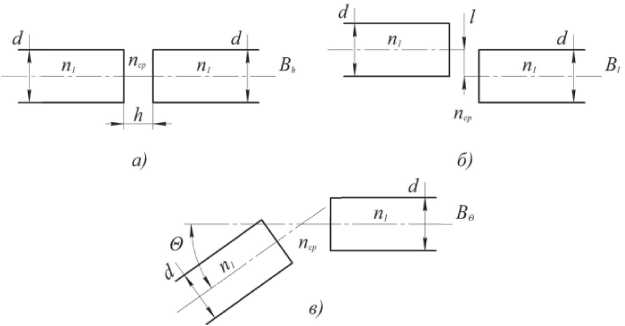
Рис. 2. Доминирующие источники энергетических потерь в ОР: а – потери при осевом смещении; б – потери при радиальном смещении; в – потери при угловом смещении

Таблица 1. Результаты вычислений значений x h _onT ^, х _юпт ^, х ₀ опт

Энергетические потери, вносимые i -ым фактором	Коэффициент влияния i -ого фактора, a i	Оптимальное значение i -ого параметра, xiopt
Bh = 2,46- Ta d	0,0049	22,7 мкм
B. = 2,77 - l d	0,055	2 мкм
B. = 2,77 —°— 0        V2-A	19,6	0,0057 рад

METHOD OF OPTIMUM CHOICE OF DESIGN FACTORS

OF SPECIAL OPTIC CONNECTORS FOR SENSOR EQUIPMENT

выражений для энергопотерь, вид которых зависит от типа оптического волокна и технологии изготовления РОС.