Методика первичной юстировки канального оптического волновода и волоконной линзы с помощью системы технического зрения

За последние десять лет произошло начальное развитие и становление производства и рынка сбыта фотонных интегральных схем (ФИС). Сигналы в них распространяются по волноводам, формируемым на подложках из фосфида индия (InP), арсенида галлия (GaAs), кремния на изоляторе (КНИ), диоксида кремния (SiO 2 ), ниобата лития (LiNbO 3 ), полимерных соединений. Для изготовления ФИС используются технологии фотолитографии, различные виды напыления и эпитаксии, изотропное и анизотропное травление. Носителем информации в ФИС является оптическое излучение. Фотонные интегральные схемы находят применение в телекоммуникационном оборудовании, в навигационных системах и комплексах, в системах мониторинга физических величин [1 –3].

На практике распространены ситуации, когда необходимо обеспечить ввод (вывод) оптического излучения в (из) ФИС. Такая необходимость возникает, если оптическая система предусматривает наличие внешнего источника излучения либо внешнего фото- приемника, а также в случае передачи оптического сигнала между несколькими ФИС. Передача сигнала в таких случаях осуществляется с помощью волоконных световодов (ВС) различных типов. Тип ВС подбирается под особенности передаваемого сигнала.

Основным критерием, характеризующим качество оптического соединения между волноводом ФИС и ВС, являются оптические потери. Минимизация оптических потерь на соединении ВС – волновод является ключевой задачей во время сборки ФИС, поскольку оптические потери снижают производительность не только каждой конкретной ФИС, но и всей оптической системы, построенной на ФИС.

В общем случае взаимное расположение ВС и волновода определяется их боковыми, продольными и угловыми смещениями [4]. Для выравнивания ВС и волновода используется юстировка. Юстировка осуществляется с помощью системы манипуляторов, которые управляют перемещением и ориентацией ВС или ФИС в пространстве. Система манипуляторов имеет шесть степеней свободы: три пространственные координаты x , y , z и три угла θ x , θ y , θ z (рис. 1).

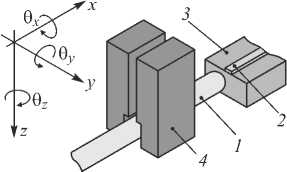
Рис. 1. Юстировка волновода и волоконного световода. 1 – волоконный световод; 2 – волновод; 3 – фотонная интегральная схема; 4 – система манипуляторов, обеспечивающая перемещение волоконного световода по трём координатам x, y, z и трём углам θ x , θ y , θ z

1.    Постановка задачи

Работа посвящена юстировке канального оптического волновода и волоконной линзы. Волоконная линза – оптический компонент, представляющий собой волоконный световод с линзой на торце (рис. 2). Свет на выходе из таких линз фокусируется на конечном расстоянии от кончика линзы, собираясь в узкий пучок. Волоконные линзы используются для ввода (вывода) оптического излучения в (из) волноводы ФИС с высоким контрастом профиля показателя преломления. Задача юстировки волоконной линзы является частным и наиболее сложным случаем юстировки волоконного световода и волновода, так как такая юстировка имеет наиболее строгие допуски по разрешению манипуляторов и требует учета фокусного расстояния линзы [5]. Обычно в ходе юстировки волоконный световод подводится к торцу чипа до касания, что не требует строгого контроля продольного смещения. В случае волоконной линзы любые касания повреждают как саму линзу, так и торец чипа, следовательно, требуется строгий контроль продольного смещения. Волоконные линзы, используемые в настоящей работе, были изготовлены на волоконных одномодовых световодах со ступенчатым профилем показателя преломления Corning SMF-28e+, диаметр фокусного пятна – около 3 мкм.

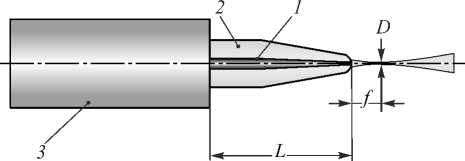
Рис. 2. Волоконная линза: 1 – сердцевина волокна,

2 – оболочка волокна, 3 – защитно-упрочняющее покрытие волокна, L – длина зачищенного участка, f – фокусное расстояние линзы, D – диаметр фокусного пятна

Традиционно юстировка волновода и ВС рассматривается исследователями как задача оптимизации, где целевой функцией выступает уровень оптического сигнала [6– 8]. Однако данные методы юстировки не работают в случае, когда ВС и волновод смещены друг относительно друга настолько, что нет возможности ввести (вывести) излучение с приемлемыми оптическими потерями. Оптические потери измеряются в децибелах (дБ), способ их расчета указан в [4]. На практике границей приемлемых оптических потерь является значение –50 дБ. В случаях, когда оптические потери превышают границу приемлемых потерь, необходима первичная юстировка.

Для первичной юстировки рядом авторов было предложено использовать методы компьютерного зрения. Например, в работах [9, 10] рассмотрен случай юстировки оптического наконечника (объект, в который монтируется массив из одного или нескольких ВС, а торец полируется) и ФИС с массивом канальных волноводов. Авторы проводят процесс бинаризации изображений, выделяют границы с помощью детектора границ Кэнни [11], а затем различными методами находят прямые, соответствующие крайним границам торцов оптического наконечника и ФИС. В работах [9, 10] рассматриваются простые объекты с формой прямоугольника или параллелограмма, а все вычисления сводятся к нахождению двух близко расположенных прямых. В нашей работе необходимо детектировать на изображениях объекты более сложной формы, поэтому методы [9, 10] не могут в ней использоваться.

Также методы компьютерного зрения применяются для юстировки двух ВС в современных аппаратах для сварки ВС [12– 14]. Методика юстировки по сердцевине с использованием профиля яркости (англ. PAS–Profile Alignment System) [12] предполагает, что коллимированный пучок света от светодиода проходит через ВС и фокусируется. При этом ВС выступает в качестве линзы. Камера, фокус которой настроен недалеко от края ВС, позволяет получить изображение с тонкой полоской в центре ВС, соответствующей сердцевине. Используя координаты данной полоски на профиле яркости, два ВС юстируются с субмикронной точностью и затем свариваются. В работе [14] представлена аналогичная методика, отличающаяся тем, что для юстировки двух ВС используются координаты центра масс границ ВС, найденных с помощью оператора Собеля. Точность юстировки аналогична методике [12]. Недостатком методик [12, 14] является строгая специализация на юстировке только волоконных световодов с торцами, сколотыми под 90° к осям ВС. В отличие от ВС, ФИС не имеет стандартных размеров, редко прозрачна для излучения подсветки, может иметь металлические или диэлектрические покрытия, погруженные или поверхностные канальные волноводы, перепады высоты. Также ФИС, за исключением образцов с подложкой из плавленого кварца, не поддается сварке с ВС средствами аппарата для сварки ВС. Методики [12, 14] не пригодны для юстировки не только ФИС, но и волоконных линз.

Целью работы является создание методики первичной юстировки волоконной линзы и канального волновода на основе алгоритмов компьютерного зре- ния. Начальным условием задачи является ситуация, когда волоконная линза и ФИС смещены настолько, что ввод (вывод) оптического излучения невозможен (рис. 3а) и, соответственно, невозможна юстировка по оптическим потерям.

а)

б)

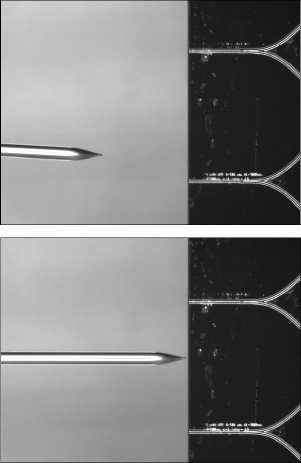
Рис. 3. Изображения области юстировки волоконной линзы и фотонной интегральной схемы: до первичной юстировки (а); после первичной юстировки (б)

На первом шаге с помощью методики необходимо определить продольное и угловое смещения волоконной линзы относительно торца ФИС с ошибками не более 20 мкм и 0,5° соответственно. Данные значения выбраны из того факта, что смещения <20 мкм и < 0,5° плохо распознаются оператором в ходе выполнения ручной юстировки на аналогичном стенде с использованием системы технического зрения. Необходимо отметить, что данные значения характерны только для стенда, используемого в ходе настоящей работы. Под угловым смещением линзы и ФИС понимается угол между нормалью к торцу ФИС и осью линзы. Затем на основании полученных данных с помощью системы манипуляторов объекты должны выравниваться (рис. 3 б ). В работе не рассматривается поиск боковых смещений между волоконной линзой и каждым волноводом, поскольку боковые смещения легко и быстро находятся в результате дальнейшей юстировки по оптическому сигналу.

2.    Система технического зрения

Состав разработанной системы технического зрения представлен на рис. 4. Волоконная линза 1, закрепленная на платформе 2, юстировалась относительно канальных волноводов 3 ФИС 4. Для точного и повторяемого расположения ФИС использовался столик 5 с вакуумным прижимом и механическими ограничителями под габариты ФИС. Платформа 2 представляла собой сборку из трех линейных и трех угловых манипуляторов. Сверху находилась камера 6 (Basler acA2500-14gc) с разрешением 5 Мп. Использовался телецентрический объектив 7 (Constrastech CLW2-MP-2.0X-110) с кольцевой диодной подсветкой. Так как процесс юстировки объектов чувствителен к вибрациям, использовалось виброизолирующее основание 8. Управление камерой 6 и платформой 2 осуществлялось с помощью персонального компьютера.

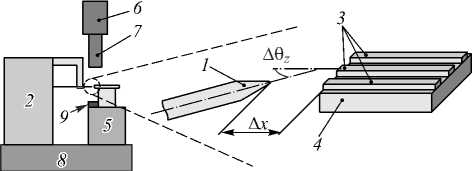
Рис. 4. Система технического зрения: 1 – волоконная линза; 2 – платформа; 3 – канальные волноводы;

4 – фотонная интегральная схема; 5 – столик; 6 – камера; 7 – телецентрический объектив; 8 – виброизолирующее основание; 9 – источник освещения (проходящий свет)

Система технического зрения сначала определяла продольное Δ x и угловое Δθ z смещения, затем эти данные передавались на управляющие модули и с помощью платформы корректировалось положение волоконной линзы.

3.    Схема освещения

Как показали предварительные эксперименты, существенное влияние на юстировку оказывали условия освещения. Для данной работы подходят две схемы освещения: в отраженном свете (камера и источник освещения находятся по одну сторону от объекта) и в проходящем свете (объект располагается между камерой и источником освещения). Так как волоконная линза прозрачна в видимом спектре, для получения контрастных границ необходимо использовать проходящий свет. При отраженном свете на изображении линзы появляются блики и затемнения.

ФИС, используемая в работе, не прозрачна в видимом спектре, для детализации элементов на поверхности необходимо использовать отраженный свет. В то же время наиболее контрастные границы ФИС получаются только при использовании проходящего света (рис. 5).

Наиболее существенным фактором выбора схемы освещения послужили ограничения на габаритные и посадочные размеры для источника освещения. Данные ограничения не являются строгими, когда ФИС не имеет корпуса. Ввод (вывод) оптического излучения в бескорпусные ФИС обычно выполняется во время тестирования оптических параметров ФИС сразу после их изготовления для отсеивания брака. В этом случае источник освещения возможно расположить как сверху, так и снизу, как показано на рис. 4.

Однако на практике устройство на основе ФИС имеет корпус, который необходим для защиты ФИС от воздействия негативных факторов окружающей среды. В силу ряда технических и экономических факторов монтаж ФИС в корпус обычно происходит до операции стыковки ФИС с ВС. В этом случае применима только схема с отраженным светом (источник освещения сверху), поскольку внутри корпуса не хватает пространства для размещения источника освещения.

а)

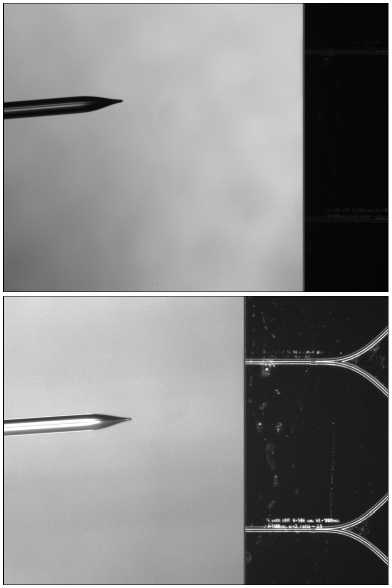
б)

Рис. 5. Изображения области юстировки волоконной линзы и фотонной интегральной схемы при использовании различных схем освещения установки: проходящий свет (а); отражённый свет (б)

В работе было отдано предпочтение схеме освещения в отраженном свете, поскольку она применима как для ФИС без корпуса, так и для ФИС в корпусе.

4.    Описание алгоритма первичной юстировки

Первичная юстировка волоконной линзы и канального волновода ФИС включает следующие стадии: подготовка и размещение образцов; поиск пространственного положения границы ФИС; поиск координат кончика и угла волоконной линзы; определение продольного Δ x и углового Δθ z смещений; перемещение волоконной линзы с помощью системы манипуляторов.

• 4.1.    Подготовка и размещение образцов

• 4.2.    Поиск границы фотонной интегральной схемы

ФИС закреплялась на столике с помощью вакуумного прижима (рис. 4). Для получения повторяемого углового положения использовались механические ограничители, смонтированные на столике. Благодаря фиксированному положению, которое обеспечивалось ограничителями, ФИС попадала в поле зрения камеры системы технического зрения.

Волоконная линза жестко закреплялась между губками пневматического захвата, расположенного на платформе. Затем с помощью системы манипуляторов она перемещалась в сторону торца ФИС до попадания в поле зрения камеры.

При правильном размещении образцов волоконная линза находилась в одной половине кадра, торец ФИС – в другой. Такое размещение требуется для деления кадра на две части: часть, где расположена волоконная линза, и часть, где расположена ФИС. Это необходимо, поскольку для поиска линзы и ФИС используются разные методы обработки изображений.

Общий алгоритм обработки изображений для поиска пространственного положения границы ФИС и поиска координат кончика и угла волоконной линзы приведен на рис. 6. Сначала осуществляется поиск границы ФИС, затем, используя полученные результаты, в другой части кадра (граница ФИС используется как линия обрезки кадра) осуществляется поиск волоконной линзы.

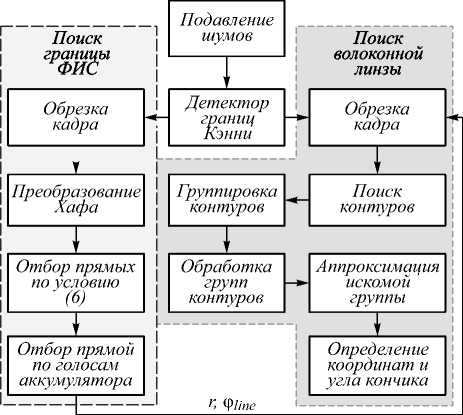
Рис. 6. Схема общего алгоритма определения пространственного положения границы ФИС и координат кончика и угла волоконной линзы

Вначале происходило подавление шумов и выполнялся поиск границ на изображении с помощью детектора границ Кэнни [11].

Детектор границ Кэнни состоит из следующих этапов: сглаживание, поиск градиентов изображения, подавление немаксимумов и двойная пороговая фильтрация [11]. Сглаживание осуществляется с помощью размытия изображения фильтром Гаусса. Сглаженное изображение обрабатывается оператором Собеля, что позволяет найти производные первого порядка. Модуль градиента и его угол определяются по формулам (1) и (2):

G = V G x + G y , (1)

0 = arctg ( G y/ G x ) , (2) где G – модуль градиента, θ – угол градиента, G x и G y – первые производные в горизонтальном и вертикальном направлениях соответственно.

После нахождения градиента отбрасываются все пиксели, не являющиеся локальными максимумами по направлению градиента. В ходе двойной пороговой фильтрации значения градиента в каждом пикселе сравниваются с верхним и нижним порогами. Если модуль градиента у пикселя выше верхнего порога, то пиксель считается белым; если ниже нижнего порога, то отбрасывается (считается черным). Если модуль градиента находится между верхним и нижним порогом, остаются только те пиксели, которые соединяются по одному из восьми направлений с соседними пикселями (проверяются восемь пикселей в окне 3 × 3, где текущий пиксель является центральным), имеющими значение градиента выше верхнего порога. В итоге, после работы детектора границ Кэнни получается бинарное изображение, где белым пикселям соответствуют границы, черным – фон.

Качество работы детектора границ Кэнни существенно зависит от выбора значений нижнего и верхнего порога по яркости. Завышенные значения порогов приводят к потере существенных границ (рис. 7в), заниженные – к большому числу границ, соответствующих незначительным перепадам яркости на изображении (рис. 7б). Для устранения зависимости качества детектирования границ от ручного выбора порогов часто для расчета пороговых значений яркости используют метод Оцу [15]. В работах [16, 17] рассматриваются усовершенствования детектора границ Кэнни, использующие в том числе автоматическое вычисление порогов (адаптивные пороги) на основе алгоритма Оцу. Для простоты часто верхний порог на этапе двойной пороговой фильтрации принимают равным порогу, определенному методом Оцу, а нижний порог – равным половине верхнего [16, 17]. В работе [16] показано, что не всегда этот упрощенный подход дает качественное выделение границ. Альтернативный подход [16] основан на предварительном делении изображения на части. Для каждой части определяется порог методом Оцу. Далее верхний TH и нижний TL пороги для алгоритма Кэнни, применяемого ко всему изображению, рассчитываются следующим образом:

n

T h = Z t i , T l = T T, (3) 2 ■ n i =1 2

где n – число частей, на которые разбито изображение, t i – значение порога, определенного методом Оцу для i -й части изображения. На рис. 7 представлены результаты выделения границ методом Кэнни при использовании различных значений порогов.

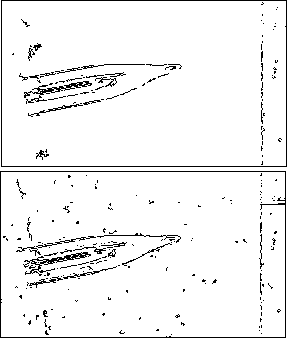
Рис. 7. Выделение границ методом Кэнни: фрагмент исходного изображения (а); результаты при различных значениях нижнего и верхнего порогов (б–е): 20:80 (б), 40:120 (в), 44:89 (г), 31:62(д), 35:71 (е); пороги заданы вручную (б, в), пороги рассчитаны упрощенным способом (г), пороги рассчитаны по формулам (3) при разбиении изображения на 4 и 9 частей соответственно (д, е)

Как видно из рис. 7, при использовании автоматического вычисления порогов удается сохранить существенные границы (границы ФИС, границы линзы). При вычислении порогов с предварительным разбиением изображения на части пороги, в целом, получаются несколько ниже, чем при расчете порогов по всему изображению. Это, как видно из рис. 7д, е, с одной стороны, приводит к уменьшению разрывов границ линзы, с другой – приводит к «лишним» границам. Соответственно, плюсы и минусы данного подхода компенсируются, и в работе далее использо- вался алгоритм Кэнни с адаптивными порогами, рассчитываемыми по всему изображению.

В приведенных на рис. 7 результатах при обработке исходного изображения шумы подавлялись лишь в детекторе Кэнни (при сглаживании изображения фильтром Гаусса), при этом не использовался предварительный этап подавления шумов (см. рис. 6). В целом, при этом удается получить довольно качественные границы в области линзы. Однако предварительный этап шумоподавления позволяет избавиться от лишних границ на изображении, что уско- ряет последующую обработку изображений. Кроме того, предварительная фильтрация позволяет снизить число различных дефектов границ в области линзы.

Для предварительного подавления шумов использовался фильтр [18]. После применения этого филь- тра можно снизить пороги Кэнни (делятся на два), это позволяет детектировать подавленные завышенными порогами существенные границы (границы линзы и ФИС) без риска детектирования большого числа лишних границ в других частях кадра.

в)

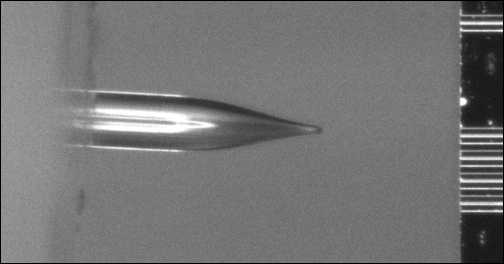
Рис. 8. Выделение границ в сложном случае с помощью детектора Кэнни: фрагмент исходного изображения (а); адаптивные пороги 89:179 (б); предварительная фильтрация шумов, адаптивные заниженные пороги 45:90 (в); ручные пороги 45:90 (без предварительной фильтрации шумов)(г)

Кроме того, занижение значений порогов позволяет детектировать границы линзы в сложных случаях, когда на изображении много резких перепадов яркости, а перепад на границе линзы меньше. В этом случае с помощью упрощенного метода расчета порогов получаются высокие пороговые значения. При этом граница линзы не детектируется (рис. 8 б ). В свою очередь, ручное занижение порогов без предварительного шумоподавления приводит к возникновению лишних границ и ложных разрывов (рис. 8 г ).

В разработанной методике юстировки для выделения границ использовалось предварительное подавление шумов фильтром [18] и детектор Кэнни с адаптивными заниженными порогами, поскольку именно такой подход позволяет получить наиболее качественные границы линзы.

Далее происходила обрезка кадра. В случае, если ФИС находилась справа от волоконной линзы, обрезалась левая половина кадра, иначе – обрезалась правая половина кадра.

После выделения границ на изображении необходимо перейти к этапу поиска линии, соответствующей торцу ФИС. Для этого с помощью преобразования Хафа [19] на полученных границах находились прямые. В полярной системе координат уравнение прямой имеет вид:

x cos ф + y sin ф = r , (4)

где x , y – координаты произвольной точки на прямой; r – расстояние от начала координат до прямой; φ – угол между нормалью к прямой, проведенной из начала координат, и осью абсцисс.

Необходимо найти значения пар r , φ, соответствующие прямым на изображении. Производится дискретизация пространства параметров r , φ, и формируется двумерный массив, именуемый аккумулятором A r ,φ . Затем осуществляется так называемая процедура голосования: для каждого ненулевого пикселя, оставшегося после применения детектора Кэн-ни, координаты которого удовлетворяют уравнению (4) с точностью до шага дискретизации в пространстве параметров, происходит накопление значений аккумулятора [19, 20]:

А г , ф = A r ,ф + 1.                                            (5)

После процедуры голосования производится поиск локальных максимумов в пространстве аккумулятора. Максимумы, набравшие число голосов больше порогового, соответствуют параметрам прямых на изображении [19, 20].

Для поиска торца ФИС среди прямых отбирались только те, чей угол удовлетворял критерию (6):

|ф line -a|<£ ,                                          (6)

где φ line – угол между нормалью к прямой и осью абсцисс, найденный с помощью преобразования Хафа;

α – угол между нормалью к торцу ФИС и осью абсцисс (обычно равен 0°); ε – предельное значение угла поворота ФИС при ее размещении на столике (± 1°). Отобранные прямые показаны на рис. 9 в .

При использовании критерия (6) учитывался тот факт, что нам известны значение угла торца α и предел угла поворота ФИС ε. Угол α полностью определяется на этапе полировки торцов ФИС и обычно является паспортным параметром ФИС. В ходе работы использовались ФИС, отполированные под 0°, хотя на практике также распространены образцы с углом полировки от 5° до 20° – такие ФИС имеют пониженный уровень обратных отражений. На значение ε влияют два фактора: конструкция столика с ограничителями и человеческий фактор. Под человеческим фактором в данном случае понимается то, с какой ошибкой человек способен устанавливать ФИС на столике. Если не учитывать человеческий фактор, то должным образом разработанный столик позволяет размещать ФИС с углом поворота в пределах ±0,5°. В данной работе выбран более широкий диапазон ε =± 1°, так как такой диапазон более характерен для лабораторных условий.

В ходе отбора по критерию (6) в большинстве случаев находились несколько прямых, которые отличались по углу φ (рис. 9 в ). Прямая с наибольшим количеством голосов аккумулятора (рис. 9 г ) принималась за искомую прямую, соответствующую торцу ФИС. По окончании поиска сохранялись значения длины радиус-вектора r и угла найденной прямой φ line .

• 4.3.    Поиск волоконной линзы

Алгоритм поиска координат кончика и угла волоконной линзы показан на рис. 6. В данном алгоритме использовались результаты, полученные с помощью детектора границ Кэнни (рис. 6). Используя значения r и φ line , часть кадра с ФИС обрезалась (кадр обрезался по линии, соответствующей границе торца ФИС). Затем выполнялся поиск контуров с помощью алгоритма [21]. Контуры представляли собой неразрывные кривые на границах, полученных с помощью детектора Кэнни. Поскольку волоконная линза в отраженном свете представляет собой неоднородный объект с бликами и затемнениями, а также из-за наличия в кадре посторонних объектов, находилось большое количество контуров (рис. 10 б ).

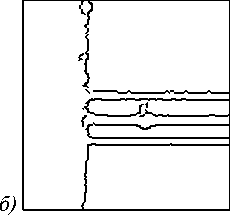
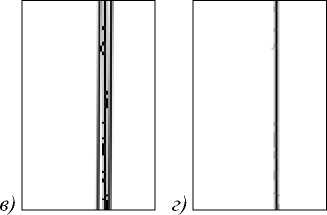
Рис. 9. Поиск границы ФИС: исходное изображение (а); увеличенный фрагмент изображения вблизи волновода с выделенными границами (б); прямые, найденные с помощью преобразования Хафа и отобранные по критерию (6) (в); искомая прямая (г)

Рис. 10. Поиск контуров: исходное изображение (а), фрагмент левой части изображения с выделенными границами (б), увеличенный фрагмент изображения контуров волоконной линзы: 1 – ложные разрывы, 2 – дублирование линий, 3 – бахрома (в)

Причины появления бликов и затемнений, а также их связь с особенностями ВС не исследовались.

Контуры с количеством точек менее порогового значения отбрасывались. Это необходимо для того, чтобы не анализировать контуры, не соответствующие границам волоконной линзы, а также возможные мелкие разрывные контуры внутри волоконной линзы. Данное пороговое значение не является абсолютным и зависит от таких факторов, как разрешение камеры, увеличение объектива, интенсивность подсветки, коэффициент усиления камеры, баланс белого и т.п. Также значение зависит от порогов, используемых в методе Кэнни (при этом не- важно, задаются пороги вручную или рассчитываются на основе метода Оцу), и от алгоритма подавления шумов. Пороговое значение необходимо определять в ходе предварительных экспериментов путем экспертного анализа качества выделения контуров, соответствующих линзе.

Как видно из рис. 10в, границе волоконной линзы нельзя сопоставить одиночный контур, т.к. возможны различные искажения контуров линзы: ложные разрывы, бахрома, дублирование линий. Таким образом, целиком границу линзы описывает не одиночный контур, а их группа. Для того, чтобы из массива контуров выделить контуры, описывающие границы во- локонной линзы, требуется выполнить предварительную группировку всех контуров изображения. Перед группировкой у каждого контура определялись координаты центра:

NN

Xc = — У х , Yc = — У У ,                (7)

C Nt1   C N² - !

где ( x i , y i ) – координаты i -го пикселя в контуре; N – количество пикселей в контуре.

Для группировки контуров использовался следующий рекурсивный алгоритм:

• 1)    Фиксировался контур.

• 2)    По всем остальным контурам осуществлялся поиск парного контура. Контур считался парным, если выполнялось следующее условие:

  • 2.1)    Евклидово расстояние между центрами контуров не больше порогового:

• 2.2)    Если не выполнялся критерий (8), то проверялось расстояние между центром данного контура и центром текущей группы контуров по условию:

• 2.3)    Если не выполнялся критерий (9), происходила еще одна дополнительная проверка. Суть проверки заключалась в том, что контур и теку-

• щая группа контуров аппроксимировались минимальными по площади прямоугольниками и в случае наличия пересечения данных прямоугольников контур считался парным.

( X C 1 - X C 2 ) + ( Y C 1 - Y C 2 ) <  P ,             ⁽⁸⁾

где p – пороговое значение. Данное пороговое значение также не является абсолютным и определяется эмпирически в ходе экспертного анализа результатов группировки контуров. Малые значения порога могут привести к разбивке контуров линзы на несколько групп, большие – к присоединению к группе контуров линзы «ложных» контуров: бахромы или контуров других фоновых объектов (в случае слишком больших значений возможно не только появление бахромы, но и захват контуров объектов, расположенных далеко от линзы).

V ( X C 1 - X g ) 2 + ( Y C 1 - Y g ) 2 <  2 ■ p,            (9)

где ( X G , Y G ) – координаты центра текущей группы контуров. При этом центр текущей группы находился следующим образом: все точки контуров группы объединялись в единый список и вокруг этих точек описывался минимальный по площади прямоугольник. Для нахождения прямоугольника использовался алгоритм rotating calipers [22], на вход которого подается не произвольное множество точек, а выпуклый многоугольник. Поэтому перед применением метода [22] в нашей работе по точкам контура строилась наименьшая выпуклая оболочка по алгоритму [23]. Центром группы контуров считался центр данного прямоугольника.

• 3)    Для каждого парного контура происходил рекурсивный вызов алгоритма группировки. И так до тех пор, пока всем контурам не была поставлена в соответствие их группа (рис. 11).

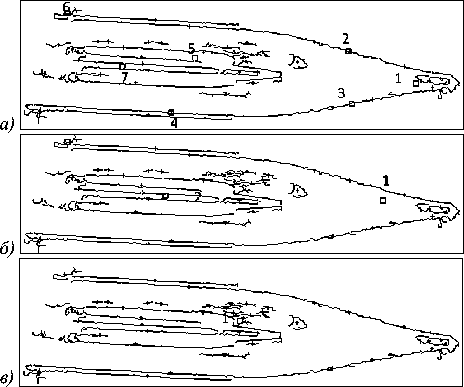
Рис. 11. Группировка контуров: одно- (а), двух- (б) и трёхступенчатые (в) алгоритмы; крестами показаны центры контуров, квадратами – центры групп контуров, цифрами – номера групп контуров

Такой трехступенчатый алгоритм необходим, т.к. одно- или двухступенчатые алгоритмы зачастую приводят к разбивке контуров, соответствующих линзе, на несколько групп (рис. 11) и, как следствие, неверному последующему определению положения и ориентации линзы относительно ФИС. Как видно из рис. 11, благодаря использованию трехступенчатого алгоритма группировки удается объединить все контуры, соответствующие линзе, в одну группу.

Далее происходила обработка групп контуров. Для каждой группы (для точек контуров, входящих в группу) находилась наименьшая выпуклая оболочка по алгоритму [23]. Нахождение наименьшей выпуклой оболочки позволило отбросить точки внутри группы контуров, которые соответствовали бликам, затемнениям внутри ВС. Причины появления бликов и затемнений внутри ВС в данной работе не исследовались. Среди оболочек выбирались только оболочки с количеством вершин не менее пяти. Данный феноменологический критерий был выбран на основании того, что волоконная линза при грубом приближении имеет форму пятиугольника и должна содержать не менее пяти вершин. Далее среди отобранных оболочек находилась оболочка с наибольшей площадью. Группа контуров, соответствующая найденной оболочке, принималась за контуры волоконной линзы.

В ряде случаев возможно присоединение к группе контуров торца феррулы, в которой закреплена линза.

Также за счет бликов и отсутствия на изображении четкой границы феррула–линза невозможно отделить выступающую из феррулы часть волокна. Обе эти проблемы (рис. 12) приводят к последующему неверному детектированию положения линзы.

Рис. 12. Проблемы при детектировании линзы: на фоне исходный фрагмент изображения (яркость фона увеличена для контрастного отображение результатов детектирования); тонкие линии – группа контуров линзы, толстая линия – наименьшая выпуклая оболочка;

вертикальная пунктирная линия – граница феррулы

Для предотвращения описанных выше проблем с присоединением к группе контуров линзы лишних контуров часть точек контуров линзы, находящихся справа от левой крайней точки линзы (если линза расположена в левой части кадра или слева от правой крайней точки, если линза расположена в правой части кадра) на расстоянии менее порогового, отсекались от контуров. Отсекаемые точки контуров игнорировались при дальнейшей обработке (при построении наименьшей выпуклой оболочки, при дальнейших шагах). Поскольку на данном этапе не определена ориентация линзы, то расстояние «отсечения» отсчитывалось по горизонтальной оси. Длина отсекаемой части (пороговое расстояние) определялась эмпирически в ходе предварительных экспериментов и зависит от разрешения изображения, степени размытости границы торца феррулы, от параметров детектирования групп контуров.

После детектирования оболочки определялись координаты ее крайней правой или левой точки ( x f , y f ) (в зависимости от того, где находится волоконная линза: если линза слева, то у правой, если справа – то у левой).

Рис. 13. Результаты детектирования волоконной линзы: толстые линии – наименьшая выпуклая оболочка и результат аппроксимации оболочки минимальным по площади прямоугольником; тонкие линии – группа контуров, соответствующая линзе

Для определения угла θf (угол ориентации волоконной линзы относительно горизонтальной оси изображения) оболочка аппроксимировалась минимальным по площади прямоугольником (рис. 13) по алгоритму [22]. В качестве угла θf принимался угол наклона прямоугольника. Альтернативный подход в определении угла линзы основан на аппроксимации методом наименьших квадратов точек группы конту- ров, соответствующих линзе, прямой. Прямая сопоставляется с осью линзы. Аппроксимация прямоугольником оказалась более стабильной и повторяемой, так как прямоугольник строился вдоль длинных сторон световода и не учитывал точки на конусном участке линзы (границы конусного участка в общем случае были более дефектными, чем границы цилиндрического участка световода).

• 4.4.    Определение смещений линзы и ФИС

Продольное Δ x и угловое Δθ z смещения между волоконной линзой и торцом ФИС определялись следующим образом (рис. 14):

r - y f ⋅ sin ϕ line

Δ x =                - x f ,                        (10)

cos ϕline где уменьшаемое определяется на основании (4), а угловое смещение Δθz следующим образом:

Δθ z =ϕ line -θ f ,                                    (11)

где r и φ line – длина и угол нормали, проведенной из начала координат к торцу ФИС; ( x f , y f ) – координаты крайней точки волоконной линзы; θ f – угол между осью волоконной линзы и осью x .

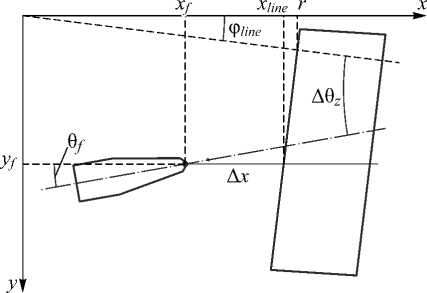
Рис. 14. Геометрические построения для нахождения продольного и углового смещений

Необходимо отметить, что расстояние, найденное по формуле (10), не является длиной перпендикуляра от крайней точки линзы до торца ФИС. Это обусловлено тем, что ось координат x кадра совпадает с осью координат x манипулятора (рис. 1), из-за чего достаточно найти проекцию на ось x .

Значение Δ x переводилось из пикселей в микрометры с помощью калибровочного коэффициента, полученного путем фотографирования и измерения размеров в пикселях объект-микрометра ОМО (производитель ЛОМО, рис. 15). Калибровочный коэффициент составил 1,1 мкм / пикс.

• 4.5.    Перемещение волоконной линзы

5.    Результаты

Полученные продольное и угловое смещения использовались для перемещения системы манипуляторов с волоконной линзой. Учитывая тот факт, что волоконная линза имела фокусное расстояние от

5 до 20 мкм (рис. 2), она подводилась не ближе, чем 50 мкм относительно торца ФИС. С одной стороны, данное расстояние гарантировало возможность ввода (вывода) оптического излучения при дальнейшей юстировке по оптическому сигналу. С другой стороны, такое расстояние было достаточно безопасным, чтобы избежать столкновения волоконной линзы и ФИС при перемещении в случае некорректного определения координат границы ФИС или кончика линзы. Столкновение может повредить как ФИС, так и линзу.

Рис. 15. Кадр с объект-микрометром ОМО (ЛОМО).

Числами показаны координаты в пикселях (x, y) двух крайних штрихов. Длина всей шкалы – 1 мм, расстояние между мелкими штрихами – 0,01 мм

Для оценки точности разработанной методики были определены абсолютные значения погрешностей (модули абсолютной погрешности) продольного и углового смещений между волоконной линзой и торцом ФИС:

^ε θ ⁼ Δθ z ист ^- Δθ z изм ^ε x ^{= Δ x}ист ^{- Δ x}изм ,

где Δθ zизм и Δ x изм – измеренные значения углового и продольного смещений; Δθ zист и Δ x ист – истинные значения углового и продольного смещений соответственно.

Поскольку в ходе эксперимента использовались прецизионные манипуляторы с минимальным шагом <0,1 мкм и <0,01°, что существенно ниже целевых допусков первичной юстировки (20 мкм и 0,5°), в качестве истинных значений продольного и углового смещений использовались координаты манипуляторов.

Было проведено две серии экспериментов. В первой серии волоконная линза продольно перемещалась относительно торца ФИС с шагом 10 мкм в диапазоне от 0 до 1600 мкм в прямом и обратном направлениях. Для определения зависимости погрешности измеряемого продольного смещения от углового смещения волоконная линза размещалась под углом 0, 1, 2, 3 и 4° к нормали к торцу ФИС.

В ходе второй серии экспериментов волоконная линза с помощью манипулятора с шагом 0,1° вращалась относительно торца ФИС в диапазоне от –5° до 5° в прямом и в обратном направлениях. Для определения зависимости погрешности измеряемого углового смещения от продольного смещения волоконная линза размещалась на расстоянии 100, 600, 1100 и 1600 мкм относительно торца ФИС. Общее время проведения каждого эксперимента составило около 10 минут. Результаты экспериментов представлены на рис. 16.

ε x , мкм 3,5

3,0

2,5

2,0

1,5

1,0

0,5

бхмакс, МКМ 4

0 250 500 750 1000 1250 1500 1750

а)                                           Δ x ист , мкм    б)

в)                                         ^zucm>

О

г)                                           Nx, мкм

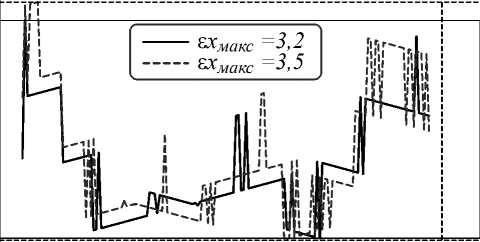
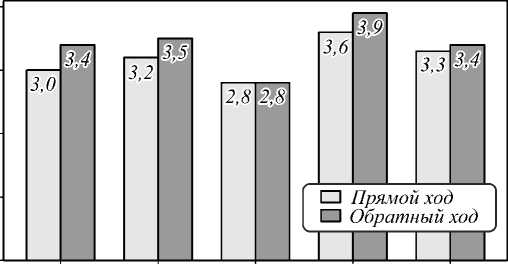
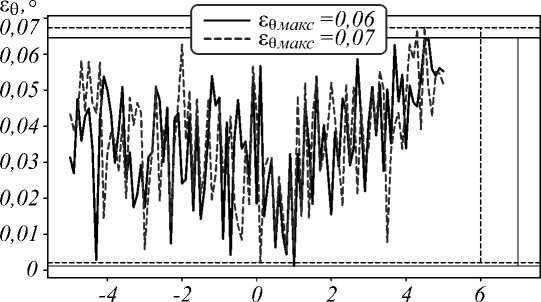
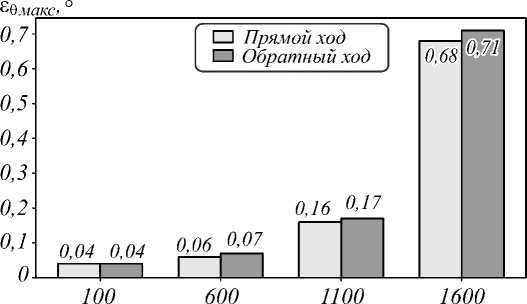
Рис. 16. Абсолютные погрешности определения смещений между волоконной линзой и торцом ФИС: погрешности определения продольного смещения при угловом смещении 1° (а); максимальные погрешности определения продольного смещения в зависимости от угла волоконной линзы (б); погрешности определения углового смещения на расстоянии 600 мкм (в); максимальные погрешности определения углового смещения в зависимости от расстояния (г); на графиках: сплошная линия – прямой ход, пунктирная – обратный ход

На рис. 16 б представлены максимальные абсолютные погрешности определения продольного смещения при углах 0, 1, 2, 3 и 4°. Из рис. 16 б следует, что угловое смещение волоконной линзы слабо влияет на ошибку в определении продольного смещения. Учитывая, что максимальная погрешность обратного хода выше, чем прямого, можно сделать вывод, что манипулятор перемещается в каждую новую точку относительно предшествующей с некоторой ошибкой, которая аккумулируется в ходе эксперимента. На рис. 16 а представлена зависимость абсолютной погрешности продольного смещения волоконной линзы в случае углового смещения 1° (для других угловых смещений графики аналогичные). Из графика следует, что, во-первых, погрешность иногда меняется на ± 1 пикс в близкорасположенных точках, во-вторых, погрешность возрастает при малых (<200 мкм) и больших (> 1300 мкм) продольных смещениях. Первое можно объяснить тем, что камера (в отличие от системы манипуляторов) не была закреплена на виброизолирующем основании (рис. 4), из-за чего она подвергалась воздействию вибраций от работающего оборудования и ходьбы персонала. Второе может быть вызвано меняющимися условиями освещения из-за изменения положения волоконной линзы в кадре.

На рис. 16 г представлены максимальные абсолютные погрешности определения углового смещения при продольных смещениях 100, 600, 1100 и 1600 мкм. Из диаграммы следует, что продольное смещение волоконной линзы сильно влияет на величину ошибки в определении углового смещения. Это объясняется тем, что чем больше расстояние между линзой и ФИС, тем меньше цилиндрического участка волокна находится в кадре, что в силу высокой дефектности границ конусного участка осложняет поиск истинного угла. Из диаграммы следует, что при продольном смещении > 1000 мкм ошибка в определении угла стремительно увеличивается. На рис. 16 в показана зависимость абсолютной погрешности углового смещения волоконной линзы в случае продольного смещения 600 мкм (для других продольных смещений графики аналогичные). Из рис. 16 в следует, что (как и на рис. 16 а ) погрешность возрастает с ростом углового смещения, что может быть вызвано меняющимися условиями освещения из-за перемещения волоконной линзы.

Таким образом, как следует из рис. 16, для уменьшения погрешностей юстировки необходимо осуществлять юстировку по алгоритму, приведенному ниже.

• 1)    Вначале вне зависимости от расстояния между линзой и ФИС необходимо найти продольное смещение. Затем переместить линзу на расстояние от 100 до 500 мкм (при которых минимальна погрешность в определении углового смещения). Диапазон от 100 до 500 мкм выбран исходя из того, что линза в ходе последующего перемещения по углу может как подвинуться в

сторону ФИС, так и отодвинуться от нее. Данное явление возникает в силу конструктивных особенностей системы манипуляторов, примененных в ходе данной работы.

• 2)    Найти угловое смещение и переместить волоконную линзу по углу.

• 3)    Сократить продольное смещение до 50 мкм. Такой подход позволит выполнить юстировку с абсолютными значениями погрешностей <4 мкм в продольном направлении и <0,05° по углу.

Заключение

Была разработана и испытана методика первичной юстировки волоконной линзы и канального волновода ФИС с помощью методов компьютерного зрения. Экспериментально показано, что методика позволяет находить продольные и угловые смещения между волоконной линзой и торцом ФИС с абсолютными значениями погрешностей <4 мкм и <0,1° соответственно. Точность методики не ограничена полученными значениями и может быть значительно улучшена изменением характеристик используемых камер, объективов и освещения.

Разработанная методика может использоваться для юстировки многих других объектов, поскольку феноменологический критерий может быть изменен и дополнен. Например, методика может быть применена для юстировки: волоконных световодов с прямыми и наклонными торцами, сферических и полусферических волоконных линз, оптических наконечников [9], дискретных оптических компонентов, полупроводниковых лазерных диодов, фотодиодов, различных ФИС между собой и др.

Результаты данной работы могут быть использованы для упрощения, повышения эффективности, производительности и повторяемости операций по тестированию и сборке фотонных, оптоэлектронных и волоконно-оптических компонентов как в лабораторных, так и в промышленных условиях.

Работа выполнена в ходе реализации проекта «Разработка и создание технологии и производства миниатюрного резонансного оптического гироскопа широкого назначения» (Договор № 2/549/2020 от 23.07.2020 г.) в рамках Программы государственной поддержки компаний-лидеров, разрабатывающих и обеспечивающих внедрение продуктов, сервисов и платформенных решений преимущественно на основе технологий и решений для цифровой трансформации приоритетных отраслей экономики и социальной сферы.