Методика получения интегральных оценок эффективности технологических систем сборки летательных аппаратов

Рис. 1. Схема дерева критериев эффективности варианта ТС сборки ЛА

Функция полезности J ( Ki ,...,Km) изменяется в интервале [0,1], причем J (К.,...,К )=0, a 1m и (к1,...,Km) = 1.

Введем дополнение к ритерия K j в виде подмножества критериев K j = {K_l,...,K_j+1,...,K_m} для определения полилинейной функции полезности на основе следующих определений.

Содержательный смысл формулы (1) заключается в построении функции полезности в зависимости от одного критерия Kj , которая является условной функцией полезности при фиксированном дополнении.

Условная функция U ( к _j - ^j ) изменяется в интервале [ J ( к j -^ j ) ; U ( к ' -^ j ) ], включает подмножества J ( к I - к^- ! ) ,

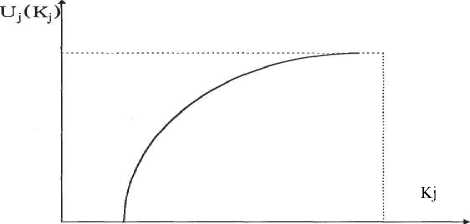
Рис. 2. Условная функция эффективности от одного критерия для варианта ТС АСП и (K j^J,Ки (к  k ).

Перейдем к другой условной функции полезности, поменяв зн ачен ие критериев, входящих в дополнение, на K j = K 2 . На рис. 3 изображена условная функция полезности с интервалом изменения

[ и ( ■       •) ; и ( к * , ^2 ) ].       (2).

Зависимость (2) означает, что две любые условные функции полезности связаны между собой положительным линейн ы м преобразованием.

Действительно: и (K j , K ) =

= и K j , ^{K j} +b( ^{K j} ) и (K j , ^Kj ) и (K j ).

и (К, K 2 ) = и ( K j , K 2 )+

+ b( K 2 ) и (K j , ^Kj );

Откуда и (Kj, K2) = a Kj и (Kj, K1) +p, (3), где a=p( K2 ) / b( Kj ); p = и (Kj- K2 ) " a и (Kj, Kj) и (Kj).

С учетом вышеприведенной интерпретации условия (3) проверка независимости эффективности критерия от своего дополнения состоит в следующем. Необходимо зафиксировать дополнение,

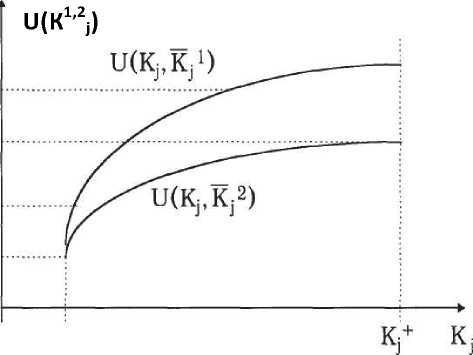
Рис. 3. Условная функция эффективности от двух критериев для варианта ТС АСП например, K 1j , и построить условную функцию полезности от одного критерия, приняв и (Kj, Kj )= 0, a и ( K^ , Kj)= l .

Такая функция является нормированной условной функцией эффективности, отражающей результат от изменения предпочтения для многокритериальной оценки объекта при изменении только одного критерия. Тогда, поменяв зн ач ения критериев, входящих в дополнение, на K 2j , вновь построим нормированную условную функцию. Если эта функция не изменяется при изменении дополнения, то выполняется условие независимости эффективности критерия от его дополнения [1]. Так как нормированная условная функция эффективности не зависит от Kj, обозначим ее как и j (K j ) .

Анализ полилинейной функции (3) показал, что при большом числе критериев m требуется определение значительного числа коэффициентов, для определения которых, в свою очередь, требуется некоторое множество оценок, а при m>4 её практическое использование затруднено.

Поэтому для анализа и оценки сложных ТС сборки ЛА сформулируем условия существования мультипликативной функции эффективности. Для этого введем следующее определение понятия независимости критериев по предпочтению.

Определение 2. Критерий K_j неза ви сим по предпочтению от своего дополнения K j , если порядок многокритериальных объектов в последовательности, образованной изменением K_j и фиксированном дополнении K 1j , не зависит от значений критериев, входящих в дополнение (1):

и (К_рК₂) и V 1 и (К1)+ V₂ и (К2)+

+(1- V 1 -V₂) и (К1) и (К2), _(4) где V₁,V₂ – коэффициенты для дополнения K j , которые могут быть представлены в табл. 1.

Сравнивая понятия независимости по полезности и по предпочтению, можно сделать вывод, что из независимости по полезности следует независимость по предпочтению.

Определение 3. Пара критериев K_j и К_i; независима по предпочтению от своего дополнения K j,i , если порядок объектов в последовательности, образованной изме не нием K_j и К_i, и фиксированном дополнении K 1j , не зависит от значений критериев, входящих в дополнение (1).

Определение 4. Критерии К_j (j=l,2, ...,m) взаимно независимы по эффективности от своего дополнения, если параметры функции эффективности не взаимосвязаны при отражении структуры ТС по рангу предпочтений .

Для автоматизации процессов анализа и получения оценок проектов перспективных ТС сборки ЛА введем понятие базиса, или системы В={Аj|jЄKij}, состоящей из m линейно независи-

Таблица 1. Формирование массива критериев эффективности проекта ТС АСП

Оцениваемые о бъ екты	K 1	K 2	К m	О ценки об ъектов
B+	К Г	K 2		1,0
В1	K t	K 2		V 1
В2	K 1	K 2		V 2
Вm	K 1	K 2		V m

мых столбцов матрицы А. Индекс iJ присвоим множеству базисных номеров оценок K?. Тогда в алгебраическом смысле в сборочном пространстве система В является базисом пространства критериев Em. В частности, любой вектор из Em единственным образом может быть разложен по базисным столбцам. Пусть Х0 базисное решение по заданным критериям. Следовательно, число элементов |J(x0)| множества J(x0) не превосходит m, поскольку система столбцов {Аj|j Є J(x0) } линейно независима. Если |J(x0)| = m, то решение x0 является невырожденным, но в противном случае (при |J(x0) < m| ) вырожденным. Соответственно, невырожденному базисному решению x0 соответствует единственный базис оценок В={Аj|jЄ J(x0)}. Для вырожденного базисного решения линейно независимую систему столбцов {Аj| j Є J(x0)} можно дополнить до базиса В={Аj|jЄJ}, J(x0)ЄJ. Вырожденным базисным решениям может соответствовать несколько базисов. Если задача связана с решением линейной системы уравнений, то матрица системы уравнений (АJm), образующих основные ограничения, может быть задана в диагональной форме, но в этом случае решение x(i)– базисное с множеством базовых номеров вида J(i) ={n+1,…,n+m}.

Указанные зависимости и построение соответствующих функций эффективности с учетом построения дерева критериев позволяют получать достаточно объективные интегральные оценки эффективности структуры и работы технологической системы сборки ЛА и ее подсистем.

Так как интегральные оценки основаны на иерархическом подходе к классификации критериев эффективности, то единичные критерии необходимо структурировать в виде дерева критериев; критерий самого верхнего уровня дерева является интегральным критерием оценки эффективности. Затем следует проводить агрегирование критериев по дереву с использованием агрегирующих функций (функций эффективнос- ти). Параметры функции эффективности определяются управляющим звеном, принимающим решения, и отражают его структуру предпочтений.

Следует отметить, что такой подход позволяет построить модель технологической системы сборки в виде ориентированного графа, а после расчета комплексных критериев итерационной процедурой может возникнуть необходимость дополнить структуру критериев новыми или исключить из нее некоторые критерии, изменить параметры функций полезности.

Реализация предложенной методики анализа и оценки ТС сборки ЛА для оценки надежности её функционирования может быть проведена на базе графа ТС сборки с введением двух или более вариантов критериев, где плотность графа определится как фактическое максимальное число смежных вершин (кликовое число) при максимальной связности вершин всего графа. В целом при нахождении всех максимально независимых системных множеств графа критериев с наибольшим числом вершин эффективно использование метода последовательного перебора независимых множеств с одновременной проверкой каждого множества на максимальность путем добавления к исследуемому множеству дополнительной, не принадлежащей ему вершины и выяснения условий сохранения устойчивости с последующим запоминанием оптимальных множеств. Использование данного метода связано с тем, что с увеличением числа вершин увеличивается объем вычислений за счет возрастания числа максимальных независимых множеств. Но вместе с тем большое число сформулированных независимых множеств удаляется из результата решений, так как они содержатся в других множествах, полученных ранее, и становятся не максимальными на данном этапе решения. Для снижения объема вычислений в этом случае применим систематический метод перебора, снижающий объем вычислении, и не требуется запоминания генерируемых независимых мно- жеств с целью проверки их на максимальность способом сравнения с ранее сформулированными множествами. Решение конкретной задачи обеспечения устойчивости системы сборки по критериям оптимизации схем и качества поставок деталей и комплектующих на сборку включает:

• -    алгоритм решения задач об оптимальном начальном запасе и графиках поставок на сборку по критерию минимума среднего запаса;

• -    алгоритм определения практического приближения к оптимальному управлению по качеству и надежности линии сборки.

При решении задачи в схемах управления запасами и поставками в детерминированной постановке считаем, что оперативный график работы сборочного производства определяем и может быть пересчитан в детерминированную интенсивность потребления элемента v(t) при 0 <  t <  T на период планирования при фактическом состоянии начального запаса х(₀) = х₀ при условиях:

• 1)    х(Т) = х(₀) = х₀;

• 2)    x(t) - 0 при 0 <  t <  T;

• 3)    u(t) - 0 при 0 <  t <  T;

• 4)    u(t) <  U m (t) при 0 <  t <  T, (5) где u(t) – интенсивность поставок элементов сборок;

Um(t) – ограничение сверху на интенсивность поставок элементов сборок, определяемая интенсивностью их производства цехами – поставщиками. Допустим, что для существования хотя бы одного допустимого u(t), удовлетворяющего условию (1), требуется, чтобы

• 2) распределение заказов и схемы поставок обеспечивают как нормальную плановую работу цехов – поставщиков, так и необходимые объёмы поставок элементов сборок в агрегатно-сборочные цехи.

Эти условия имеют важный производственно-экономический смысл в самолетостроительном производстве, где часто вводятся конструкторско-технологические или другие изменения, и часть неиспользуемого задела деталей отправляется в металлолом. Следовательно, для каждого из случаев (6), (7), (8) ищем минимум на множестве всех допустимых x₀(t) и w(t), 0 <  t <  T.

Анализ показывает, что если решение (5) при x0 = 0 получено со знаком равенства, то критерий оптимальности по начальному запасу определяется по формуле:

T

x* = - min [ |U (t) - v(t)|" dt - 0 •(10)

• ⁰       0 <  t <  T J ^{1 m 1}

Обозначим U*(t) –фиксированное значение объёма поставок U_m(t) на интервале в момент времени t, 0 <  t <  T.

Рассмотрим случай, когда (5) выполняется со знаком строгого неравенства. Тогда функция v(t) является кусочно – непрерывной, соответственно допустимое управление по U(t) определяется также в классе кусочно-непрерывных функций. Аналитическое представление оптимального запаса после преобразований расчетных формул имеет вид:

TT x 0 + J U m (t) " dt - J v(t) " dt = V, (6)

**

x0 = max< 0,

где V – общий объём поставок, при этом

T

min J|U ( t) - v(t)| "d(t) k .(10)

0 <  t <  T ^{1 m                 1}

dx dt

Тогда критерии оптимальности (К1, К2,…, Кj) Є {Х-}, имеющие определенный физический смысл, сформулируем в виде:

U(t) - v(t)

Для расчета соответствующего оптимального управления по U*(t) интервал [0, T] предста-

^_ 1 ^T

x = —J x(t) " dtT0

max x(t) = —

0 <  t <  T

--> min ■

;

--> min ;

T

J x(t)

- x

" dt

min

Для реализации интегральной методики оценки следует решить задачи оптимальных поставок элементов сборок по двум условиям:

1) надежность и устойчивость ТП должны соответствовать проектным показателям;

вим в виде дискретных отрезков со знакопостоянным значением функции w(t) = Um(t) – v(t).

Допустим, (ai, bi) – открытые множества, покрывающие [0, Т] в количестве imax, на которых функция w(t) < 0.

Принимая, что w(0) > 0, w(T) < 0, получаем:

a_i =0, b_i = с_i , d_i-₁ =a_i для всех i =1, 2, …, ^d i max ^{= T.}

Обозначив

imax, при этом

i max                          i max

A = U (a . , Ь . ) , C = U (c i , d i ) , (11) i = 1                                              i = 1

Получим U * (t) = U _m (t) для всех t E C на множестве С.

Для изучения поведения U* (t) на множестве А считаем, что начиная с некоторого номера i’ , вид U* (t) на интервалах (ai, bi), i = i’ , …, imax заранее известен. Тогда на интервале

^(ai - 1 ’ ^bi - 1 ) при соотношении:

b .                                                                                 1- i -1                                                                                              1

J [ U_m(t⁾-v(t⁾ ] • dt <  x" + J | v (t⁾-U ’ (t^{) ]} dt (12)

получим:

U*(t) = Um(t) для t e (ar-1,bi-1). (13)

В противном случае решение уравнения (12) относительно t представим :

b .

i 4Г

J ^{[ U} m ⁽ O ^- v^h ^d ^ <  x ** + J ^[ V ^{(t) -} U (t)^ dt . (14)

• a.b.

i -1i

Рассмотрим решения уравнения для t . . 1 , когда (a _ , < t , < b _ ,) .

i - 1 i - 1 i - 1

Для этого случая оптимальное управление на интервале (a i._ 1 , b i._ 1 ) будет иметь вид:

v(t), если a , < t < t , v 77 i -1 i -1

^U m(t) ’ если ^t i ' -1 <  t <  ^b i ' -1 ⁽¹⁵⁾

ЗАКЛЮЧЕНИЕ

Полученные аналитические представления дискретных управлений на всех подмножествах интервала [0, T] обеспечивают информационную базу принятия решений по результатам анализа и оценки текущей информации для состав- ления и корректировки оптимального графика поставок U* (t) и построения вариативных алгоритмов решения задачи об оптимальном начальном запасе и разработке графика плановодиспетчерского обеспечения поставок элементов сборок в агрегатный цех по задаваемому интегральному критерию.