Методика получения корреляционных функций случайных импульсных последовательностей
Автор: Фомин Лев Андреевич, Жук Александр Павлович, Скоробогатов Сергей Александрович, Романько Денис Владимирович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 3 т.8, 2010 года.
Бесплатный доступ
Предложена методика получения аналитических выражений для определения нормированных автокорреляционных функций случайных импульсных последовательностей, позволяющих производить оценку времени корреляции с целью выявления последовательностей, обладающих «хорошими» корреляционными свойствами для использования их в системах передачи информации, и последовательностей, обладающих свойством самоподобия для моделирования трафика в сетевых структурах
Долговременная зависимость, автокорреляционная функция, время корреляции, моделирование
Короткий адрес: https://sciup.org/140191409
IDR: 140191409 | УДК: 621.391
Текст обзорной статьи Методика получения корреляционных функций случайных импульсных последовательностей
Технология многостанционного доступа с кодовым разделением каналов (Code Division Multiple Access – CDMA) получает все более широкое распространение в современных системах радиосвязи различного назначения. Системы такого рода используют для передачи информации по каналу связи шумоподобные сигналы (ШПС). Благодаря уникальной кодовой структуре каждого из используемых ШПС, они могут быть переданы одновременно в общей полосе частот и при этом эффективно разделяться на приемном конце [2].
Сегодня технологии CDMA находят применение в сотовых системах подвижной связи, системах беспроводного абонентского доступа, спутниковых системах подвижной связи, беспроводных ЛВС и др. Данная технология легла в основу большей части проектов стандартов, разрабатываемых для глобальных систем подвижной связи третьего поколения (IMT-2000), развертывание которых уже началось.
Важными особенностями технологии СDMA, определяющими ее столь широкое распростра- нение, являются возможность обеспечения устойчивой связи в условиях действия комплекса помех и достижение конфиденциальности при обмене информацией между пользователями.
Конфиденциальность передачи сообщений по радиоканалам может быть достигнута путем обеспечения:
-
- энергетической скрытности сигналов – переносчиков информации;
-
- структурной скрытности этих сигналов;
-
- информационной скрытности самого сообщения.
Энергетическая и структурная скрытность являются важнейшими характеристиками сигнала, применяемого в системе радиосвязи. Энергетическая скрытность характеризует способность противостоять мерам, направленным на обнаружение сигнала разведывательным приемным устройством. Оценка энергетической скрытности системы радиосвязи с ШПС показывает, что чем больше ширина спектра ШПС, тем больше время анализа в обнаружителе сигнала. Кроме того, время анализа растет при увеличении требуемого отношения «сигнал/шум» на выходе обнаружителя. В результате оказывается, что эффективным средством повышения энергетической скрытности является расширение спектра ШПС до значений, определяемых отводимым на систему в целом частотным ресурсом.
Наряду с обнаружением ШПС возникает задача определения параметров, в частности, нахождения структуры и метода формирования сигнала. Под структурной (сигнальной) скрытностью понимают степень затруднения определения структуры обнаруженного сигнала. Сигнальная скрытность, в первую очередь, обеспечивается выбором сигнала, по возможности близким по внешнему виду к фону. Для радиолиний, у которых фоном является гауссовский шум, в качестве такого сигнала используют фазоманипулирован-ный ШПС, шумоподобность которого достигается при помощи псевдослучайных кодирующих последовательностей (ПСП), имеющих статистически вид случайных.
В [1] показано, что путем функциональных преобразований случайных функций может быть получено достаточно большое число ПСП раз-личноговида с числом символов N , которыемогут быть использованы для передачи сигналов в системах CDMA, а также для моделирования работы системы массового обслуживания, находящейся под воздействием самоподобного трафика. Число таких последовательностей определяется общим количеством функций f ( x ), выбранных для преобразования, а также видом функции X = ф^т\ с помощью которой данное функциональное преобразование производится [7]:
g(r)=H^/Mr)L где функция V обратна функции Ф , то есть .
Интервал времени между импульсами т , определяющий статистические свойства процесса, задается выражением [1]:
т = ф\р"' \rnd - F(a)]}, где F\x^ = jW rnd – функция формирования случайных чисел, равномерно распределенных в интервале [0; 1].
Существует множество реализаций функций формирования случайных чисел [8], конкретное воплощение которых также позволяет увеличить количество отличающихся последовательностей различной длины Nj , например, метод вычетов. Если задать некоторое начальное число у в форме несократимой дроби Уо = m0 / М , где m 0 и М – целые числа, а М взаимно простое число с некоторым целым числом q , то все последующие числа 7к будут несократимыми дробями 7к = mk /М, где числитель mk определяется как
^к+1 =утА-]— ^V-M, (1) причем обратные квадратные скобки означают, что берется наибольшее целое число, не превышающее результат выполнения действий в скобках.
Формула (1)является рекуррентной и позволяет получать последовательности псевдослучайных це- лых чисел, равномерно распределенных в интервале [0; 1].Получаемые последовательности являются циклическими,так какчерез определенное количество шагов числа начинают повторяться.Удовлетворитель-ная последовательность целых чисел получается при q = 517; M = 240,при этом длина неповторяющейся последовательности составляет F = 2,75-10n чисел.
Для количественной оценки и качественного описания полученных ПСП используются статистические характеристики второго порядка,при этом корреляционная функция является главным критерием, относительно которого определяются свойства про-цесса.Кроме того,нормированная автокорреляционная функция процессов,описывающих поведение реального трафика, позволяет производить оценку времени корреляции,которое используется для прогнозирования самоподобных процессов.
В [6]приведена задача определения нормированной автокорреляционной функции,времени корреляции дискретногослучайногостационарногопроцесса при условии,что вероятность попадания заданного числа событий на интервал Т известна и подчиняется закону Пуассона.Однако не приведен порядок вычисления данной вероятности в случае,если рассматривается произвольный закон распределения интервалов времени между событиями.
Целью статьи является разработка методики оценки корреляционных свойств случайных импульсных последовательностей,полученных путем функциональных преобразований [1],которая позволит на основе оценки вероятности попадания заданного числа событий на интервал Т получать аналитические выражения для определения нормированных автокорреляционных функций полученных последователь-ностей,позволяющих производить оценку времени корреляции с возможностью выявления последова-тельностей,обладающих «хорошими» корреляционными свойствами для использования их в системах передачи информации,и последовательностей,обла-дающих свойством самоподобия для моделирования трафика в сетевых структурах.
Постановка задачи
Рассмотрим реализацию случайного процесса, приведенную на рис. 1.
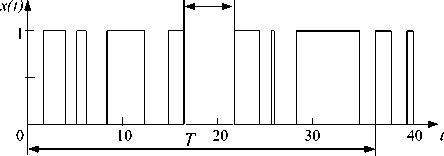
Рис. 1. Реализация случайного процесса
Функция х ( t ) представляет собой последовательность прямоугольных импульсов постоянной амплитуды (высотой 1) и случайной длительности, причем интервал времени между импульсами также является случайной величиной (телеграфный сигнал).
Обычно такие процессы можно описать двумя способами [7]:
-
- через распределение длительности интервала времени т между опрокидываниями;
-
- с помощью вероятности попадания на интервал Т определенного числа опрокидываний.
Наиболее часто применяется первый способ задания случайного процесса (см. рис. 1), поскольку чаще всего известен интегральный и дифференциальный закон распределения длительности г, например,
G(t) = F(t)
и gW=G'(T)- (2)
Однако для нахождения корреляционной функции процесса (см. рис. 1) необходимо знание второго способа задания функции, а именно
P^I^x^Y (3)
Решение задачи
Рассмотрим случайную величину τ, определяющую промежуток времени между двумя произвольными смежными событиями (опрокидываниями) в потоке событий, и найдем ее функцию распределения [7]:
G^ = P^t Перейдем к вероятности противоположного события, определяющей вероятность непоявления на интервале г ни одного события потока: Р,(Г)=1-С(Г)=/=(Г<Г),(5) откуда G(r)=l-P(r),(6) плотность распределения которого равна gY)=G'Y)=-^-pATY ат Поскольку функция Vo^ известна, можно найти вероятность попадания на интервал Т ровно n событий потока, имея в виду, что по условиям нормировки ^л?»^ =1- (7) руг\ Полагая f^=?3FY разложим функцию у Yr) в ряд Тейлора (Маклорена) по степеням τ в точке 0: /(^)= £^/(n,(o)- (8) я = 0 И- Разложению в ряд Тейлора могут быть подвергнуты все функции без исключения, если для этих функций существуют производные высших порядков [7]. При этом вероятность попадания на интервал Т заданного числа событий n равна рЛтЬ^У^Ро^У (9) Таким образом, распределение опрокидываний, которые в данном случае можно считать независимыми, подчиняется закону (9). Корреляционные функции представляют собой совокупность корреляционных моментов двух случайных величин х1 и х2 в моменты времени t1 и t2, причем оба момента рассматриваются в любом сечении всех возможных значений аргумента t случайного процесса. При достаточно большом числе m реализаций корреляционная функция может быть найдена усреднением полученных по данным реализациям произведений вида [6]: [.тХ?1)-^2)Ь то есть BQvt,J= 2 ^jcAt^jYiWi^i) '=1 7=1 Для оценки статистической связи между значениями случайного процесса в различные моменты времени вводят понятие корреляции стационарного эргодического случайного процесса, определяя функцию автокорреляций следующим выражением: Суммирование необходимо вести по всем возможным состояниям процесса (переходам). В процессе на рис. 1 таких состояний четыре (см. таблицу 1). Таблица 1. Варианты состояний (переходов) случайных процессов № n/n x. Xf+T 1 0 0 2 0 1 3 1 0 4 1 1 Так как при использовании значений хt и хt+Т, соответствующих первым трем состояниям, произведение XtXt+T выражения (10), стоящее перед знаком суммы, обращается в ноль, АКФ определяется всего одним членом: эта вероятность ^(0=^(0) = ^ то есть время пребывания процесса в состоянии ноль равно времени пребывания процесса в состоянии еди- ница. Условие (13) говорит о том, что оптимальные сигналы в смысле «хороших» корреляционных свойств следует искать среди сигналов, которые удовлетворяют условию M = Po , а величина Bo называется оптимальным числом блоков [3]. Для нахождения нормированной функции корреляции ПСП определим среднее значение данной последовательности x = ^iP^i) =1 -^W+0 -^(o) ^ ^ ^ 0,5 B^ = xtxt+T=P^xt =t^+r =1)1-1. (11) Определим вероятность P(%, =U,+r =1), которая равна произведению вероятности того, что в момент t имеет место событие хt = 1, на вероятность того, что за время Т произойдет четное число опрокидываний, так как только в этом случае хt = 1 и хt + Т = 1. При достаточно большом n и дисперсию [6] Найдем значение коэффициента корреляции (r)^ СУ Время корреляции определяется из равенства Bx, = U,.r = 1)=Л1)- IfM (12) r„ =yir(T)dT. В формуле (12) 2>,(r) вычисляется по всем четным членам разложения. Если функция является функцией общего вида (не является четной или нечетной), то для нахождения ее разложения по четным членам необходимо вычислить разложение функции /(— T). Это разложение имеет вид: л-т)= £(-i)'^/""(o), n = 0 H 1 тогда 22 co rpn CO rpn y^.W= ^/"W К-!)"^/'"^). n-o »-0 ^’ /г-O ^* Вероятность P(1) определяет априорную вероятность нахождения процесса в состоянии единица. Очевидно, что при оптимальном числе блоков [3] ПСП, определяемом выражением Л-|(Л1 + 1) Методика оценки корреляционных свойств случайных импульсных последовательностей В общем случае методика оценки корреляционных свойств включает следующие этапы. 1. Задание интегрального и дифференциального законов распределения исследуемых функций, выражающих распределение длительности интервалов между событиями (опрокидываниями). 2. Вычисление вероятности попадания на заданный интервал времени Т определенного числа событий для исследуемой функции по выражению (9). 3. Вычисление нормированной корреляционной функции исследуемого процесса по выражению (14). 4. Определение времени корреляции исследуемого процесса по выражению (15). 5. Оценка полученных значений времени корреляции исследуемого процесса с учетом выбора его максимального значения. Результаты исследований Результаты выполненных исследований сведены в таблицу 2. В первой и второй рабочих строках таблицы взяты в качестве примера широко используемые законы распределения (интегральный и дифференциальный) исследуемых функций: закон Парето, закон Вейбулла, экспоненциальный и логарифмический законы, причем во второй строке изображены графики соответствующих функций. Эти законы выражают распределение длительности интервалов между событиями (опрокидываниями), то есть соответствуют традиционному описанию трафика (первый способ описания случайных потоков). В четвертой строке таблицы приведены реализации соответствующих процессов в виде телеграфного сигнала,причем интервал времени между опрокидываниями задается формулами, помещенными в третьей строке. Реализации процессов построены в среде M athcad 2001 Professional. Формулы вероятностей попа- Таблица 2 Закон Парето Закон Вейбулла Экспоненциальный закон Логарифмический закон 1.Законы распределения интервалов времени С(г) = 1-Ю gW^'V^ О(р = 1-е^ g(r) = /Ю/т G(r)=l---г 1п^\ + 2г) ^^ (1 + Ят)/и2(1 + 2т) 2. Графики законов распределения интервалов времени к HlLl 1 1 l^-^W...... ..-— •w—"1 3. Значения Т 1 т = 1 2 (1 - г nd (1))« Т = —In-----77 _Х \-rnd\Vp 1 , 1 Т = — in------77 X \-rnd^ 4. Реализации процесса илю о i i so joo ж ■ НИ11И11 о а чо чп л я 0 ii! Illi SO ООО 250 5. Законы распределения опрокидываний Л (Г) p(r) fkMf А ( ^ J (АГ)" Р„(г)=^р4г' п\ ^ = ®_е" п\ 2/7 1п(1+ЯГ) 6. Автокорреляционная функция 5(7)= 2<ЛГ)" В(т) = Ър5(\ + е^^ В^= 0,25(1 + е'2ЛО в(т}= v 7 1п(1 + 2Г) 7. Графики S(t) 1,,. 8. Графики Г^Г) ' К в) Я » Ж С в г ^Г--------------------- Г"™1 о а ««пяжаавг о к 41 нс л я та so ео ев г 9. Время корреляции Тк ч =°° тк = 0,627 при 2 = 1, р = 2 тк = 0,5 при 2 = 1 тк =°° 10. Показатель Херста Н 0,70 0,73 0,5 0,68 дания на заданный интервал определенного числа событий приведены в пятой строке таблицы (второй способ описания случайных импульсных потоков). Здесь же приведены формулы для функции корреляции упомянутых процессов,полученные с использованием методики,изложенной в данной статье. Для вычисления разложения по четным членам в функции Вейбулла использована традиционная процедура вычисления рядов Тейлора для f (x) и f (–x) [5]: которая при P = 1 переходит в разложение экспоненциальной функции. Поскольку функция Парето не может быть разложена в ряд Тейлора, для вычисления ЪРАП использовано разложение по членам геометрической прогрессии, общий член которой задается как a 1 - (ЛГ)' (Я т)“ , а модуль прогрессии определяется как Для вычисления функции корреляции логарифмической функции использованы следующие разложения: Для получения разложения по четным членам достаточно взять сумму обоих логарифмов с обратным знаком, а именно 1 1 ^х2" In--- = — Л— 1-х- 2^2/7 Графики для коэффициентов корреляции указанных процессов, построенные с использованием программы Matlab, приведены в восьмой строке таблицы 2. В десятую строку таблицы 2 включены значения показателя Херста для всех четырех законов распределения, характеризующего степень самоподобности сформированных импульсных последовательностей, оценка значе- ний которого произведена по величине нормированного размаха (R/S статистика). Выводы 1. Получена методика, позволяющая на основании оценки вероятности попадания заданного числа событий на интервал времени получать аналитические выражения для определения нормированной автокорреляционной функции последовательностей, полученных путем функциональных преобразований, которая используется для оценки времени корреляции. 2. Исследование времени корреляции рассматриваемых процессов показывает: - чем больше Тк,, тем больше проявляетсядол-говременная зависимость, что говорит о наличии самоподобия в исследуемых последовательностях и определяет возможность их использования для моделирования работы системы массового обслуживания при обработке самоподобного трафика [4]; - уменьшение Тк позволяет говорить о последовательностях, обладающих «хорошими» корреляционными свойствами, и при проведении дополнительных исследований возможно их использование в системах передачи информации.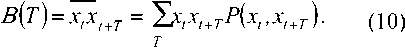
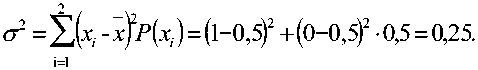
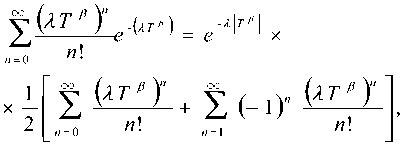
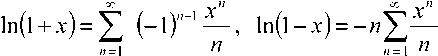
Список литературы Методика получения корреляционных функций случайных импульсных последовательностей
- Фомин Л.А., Жук А.П., Черняк З.В., Скоробогатов С.А. Использование функциональных преобразований случайных процессов для синтеза сигнальных кодовых конструкций//Информационно-измерительные и управляющие системы. Т.7, №3, 2009. -С. 82-87.
- Общесистемные вопросы защиты информации. Под ред. Сухарева Е.М. М.: Радиотехника, 2003. -292 с.
- Варакин Л.Е. Теория систем сигналов. М.: Сов. радио, 1978. -304 с.
- Шелухин О.И., Тенякшев А.М., Осин А.В. Фрактальные процессы в телекоммуникациях. М.: Радиотехника, 2003. -408 с.
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Физматлит, 2003. -807 с.
- Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982. -622 с.
- Вентцель Е.С. Теория вероятностей. М: Асадема, 2003. -571 с.
- Ермаков С.М. Метод Монте-Карло и смежные вопросы. М.: Наука, 1971. -327 с.


