Методика построения математической модели группы роботов, выполняющих комплексную задачу

В настоящее время сфера робототехники характеризуется расширением области применения мобильных роботов в промышленности, медицине, бытовой сфере и в военном деле. Роботы используются в первую очередь там, где жизнедеятельность человека либо затруднена, либо вообще невозможна, например в зонах радиоактивного или химического загрязнения, в условиях боевых действий, при проведении подводных или космических исследований и т.п. [8]. Увеличение сложности комплекса решаемых задач, возложенных на робототехнические комплексы, обуславливает снижение эффективности использования дорогостоящих одиночных мобильных роботов. Использование групп роботов для решения этих задач повысит эффективность применения роботов.

Исследованием проблем группового управления занимаются многие ученые России, среди них: Каляев А.В., Юревич Е.И., Карпов В.Э., Капустян С.Г., Гайдук А.Р., Пшихопов В.Х., Городецкий В.И., Проталинский О.М. и многие другие, за рубежом также уделяют этому вопросу много внимания. Преимущества группового применения роботов очевидны. Во-первых, это больший радиус действия, во-вторых, расширенный набор выполняемых функций, и, наконец, более высокая вероятность выполнения задания, достигаемая за счет возможности перераспределения целей между роботами группы в случае выхода из строя некоторых из них.

Целью работы является повышение эффективности управления группой мобильных роботов, выполняющих комплексную задачу.

В этой статье мы опишем методику построения математической модели группы роботов, выполняющих комплексную задачу.

Сформулируем основную задачу группового управления - это совместное, связанное управление несколькими роботами с целью выполнения общей недекомпози-рованной комплексной задачи с определенным распределением между ними отдельных ее частей.

В общем случае процесс решения задачи посредством группы роботов можно представить в виде следующей схемы.

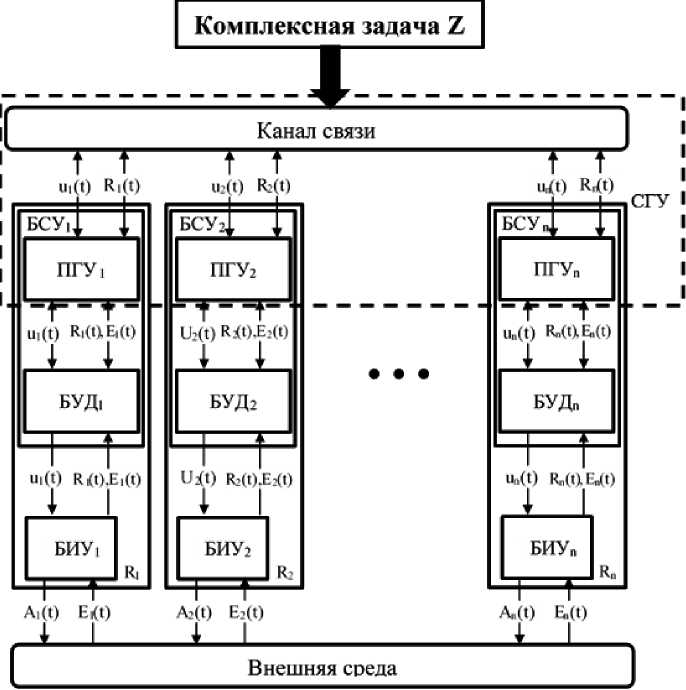
Рис. 1. Схема процесса управления группой роботов, где БСУ - бортовая система управления;

ПГУ - подсистема группового управления;

БУД - блок управления действиями;

БИУ - бортовые исполнительные устройства;

СГУ - система группового управления;

E ( t ) - вектор-функция состояния окружающей робота среды;

R ( t ) - вектор состояния робота;

u ( t ) - управляющее воздействие;

A ( t ) - вектор-функция действия робота на окружающую его среду

Задача управления группой роботов R сводится к формированию управляющего воздействия U для решения группы задач Z за фиксированный промежуток времени τ с максимальным качеством Q . При этом общий случай управления группой роботов не учитывает взаимовлияния задач друг на друга, а также различную ценность их выполнения. Вследствие этого управление группой мобильных роботов в общем виде нельзя использовать при управлении мобильными роботами, выполняющими задачи, которые обладают разной ценностью [9].

Для формулирования задачи управления в частном виде выделим входные и выходные параметры для группы роботов, каждого из роботов, группы задач и каждой из задач.

Определены входные параметры системы группового управления роботами. Основными параметрами каждой из задач Z_n множества Z являются:

• –    P_n – цена задачи Z_n ;

• -    е П - необходимые энергозатраты для выполнения задачи Z_n ;

• –    взаимовлияние задачи Z_n на остальные задачи множества Z .

Основными параметрами множества задач Z являются:

• –    N – количество задач в множестве Z ;

• –    Q _max – максимальная суммарная ценность задач множества Z .

Основным параметром робота Rm множества R является его энергоемкость е rm , при этом данный параметр зависит от времени работы робота е mm = f ( t ) . Дополнительным параметром робота - критическое значение энергоемкости е m , при котором робот не может выполнять последующие задачи и отправляется на базу [10].

Тогда частная задача общего случая управления группой мобильных роботов примет вид: для группы роботов R необходимо выбрать управляющее воздействие – стратегию, для распределения взаимодействующих задач (декомпозированной комплексной задачи) Z , обладающих ценностью P , обеспечивающих максимум функционала Q за время t .

• V R m , Z n , S : Q X max

Zk

Q = £ P; S = Z_k; Z_k e Z; Z = { Z,\P } ; n » m .              (1)

i = 1

Отличительной особенностью поставленной цели в сравнении с классической задачей является взаимосвязь задач внутри множества.

Для решения этой задачи к сложной системе «группа роботов – множество задач» применен теоретико-множественный анализ, в результате которого разработана объектно-множественная модель группы роботов, выполняющих комплексную задачу (рис. 2).

Структура множества Z состоит из пяти уровней. Первый уровень – единая неде-композированная комплексная задача с сетевой внутренней структурой, поставленная перед группой роботов; второй уровень – состояние задач: на данном уровне представлены три подмножества, в которых распределены элементы множества задач Z в зависимости от состояния: ждущие выполнения, выполняемые, выполненные; третий уровень – семейство подмножеств целевых задач роботов; четвертый – семейство подмножеств, выражающих взаимовлияние задач друг на друга; пятый уровень состоит из элементарных задач.

Проведя анализ разработанной объектно-множественной модели, мы сформулировали ограничения, которые являются существенными для группы роботов в процессе выполнения комплексной задачи:

• 1)    любые два робота не могут выполнять одну и ту же задачу;

• 2)    два робота не могут выполнять две разные задачи, результат которых приведет к выполнению одной и той же задачи;

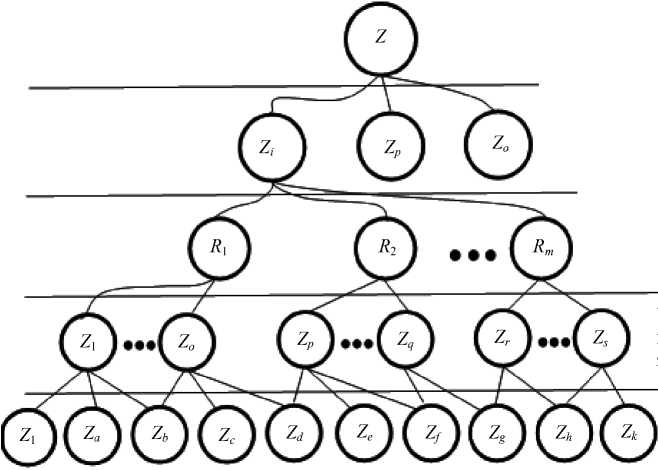
Уровень комплексной задачи

Уровень состояния задач

Уровень роботов (целевых задач)

Уровень взаимодействия задач

Уровень элементарных задач

Рис. 2. Объектно-множественная модель группы роботов, выполняющих комплексную задачу

• 3)    план выполнения работ роботом может быть скорректирован в дискретный момент времени, зависящий только от изменения состава группы;

• 4)    изменение состава подмножества задач для выполнения производится при достижении общей суммы цен выполненных задач к заданному уровню эффективности выполнения;

• 5)    робот может выполнять задачи только до тех пор, пока уровень его энергоемкости превышает критический уровень.

Кроме того, в данной работе сделаем допущение, что все цели являются достижимыми.

Проведя обзор и анализ существующих методов управления группой роботов и учитывая выявленные ограничения, мы сделали вывод о целесообразности применения многоагентного подхода в качестве основы для разработки математической модели группы роботов, выполняющих комплексную задачу.

Для дальнейших исследований введены ограничения: группа роботов функционирует в стационарных условиях; в рабочей зоне действия группы нет динамических препятствий (роботы группы не являются динамическими препятствиями друг для друга), такт управления – время, в течение которого состав группы постоянен (изменение состава происходит при неисправности робота, снижении энергоресурса до критического значения), цена задачи задана заблаговременно лицом, принимающим решение (ЛПР).

Для оценки эффективности выполнения задачи группой мобильных роботов используем следующие показатели: скорость выполнения задачи, расход энергоресурса и качество выполнения работы.

Для решения задачи распределения множества целей среди группы роботов необходимо разработать методику, позволяющую строить многокомпонентную матема- тическую модель группы мобильных роботов на основе информации, вводимой ЛПР и полученной с датчиков.

Для реализации методики построения многокомпонентной математической модели необходимо разработать и описать структуру и составные модули разрабатываемой модели.

Построенная математическая модель должна обеспечивать решение следующих задач:

• –    расчет основных текущих показателей объекта, которые могут быть представлены аналитически (оценка выполненных задач группы роботов в целом или каждым из роботов в частности, уровень оставшегося энергоресурса робота и т.д.);

• –    расчет основных измеримых показателей;

• –    расчет эффективности управления группой мобильных роботов.

Входными данными для комплексной математической модели являются: информация о множестве взаимосвязанных задач и группе мобильных роботов R . Выходными данными является информация об эффективности выполнения множества задач группой мобильных роботов. Исходя из этого, обобщенная структурная схема комплексной математической модели группы мобильных роботов примет следующий вид (рис. 3).

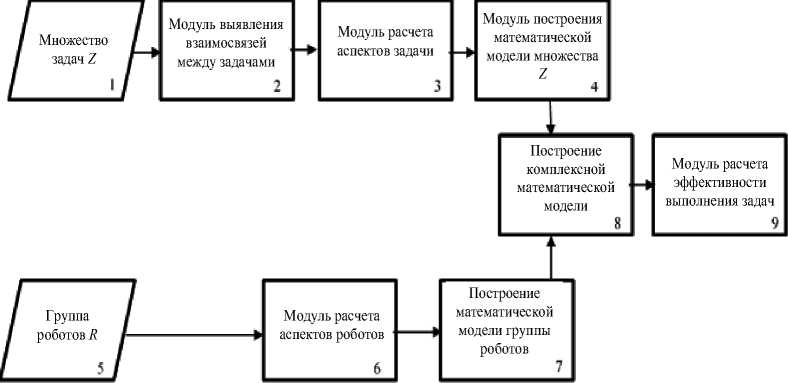
Рис. 3. Обобщенная структурная схема комплексной математической модели группы мобильных роботов

Опишем структуру математической модели и общие принципы ее работы. Входная информация о множестве задач Z (блок 1) поступает в модель выявления взаимосвязей между задачами (блок 2), где определяется атрибут задач предок/потомок. Далее информация поступает в модуль расчета аспектов задачи (блок 3), где проводится расчет параметров задачи, таких, как время выполнения задачи и необходимая энергоемкость. На основе полученных данных строится математическая модель множества задач (блок 4). На следующем этапе математическая модель дополняется информацией о группе мобильных роботов, полученных от модуля расчета основных показателей робота (блоки 6–7), на основе чего формируется общая комплексная модель группы мобильных роботов, выполняющих комплексную задачу (блок 8). Результатом расчетов по математической модели будет эффективность возможного выполнения множества Z каждым роботом из группы R .

Таким образом, методика построения математической модели группы роботов, выполняющих комплексную задачу, состоит из девяти основных этапов:

• 1)    формализация входной информации о множестве задач;

• 2)    определение взаимосвязей между задачами;

• 3)    расчет характеристик задач на основе фреймовой модели (структура знаний для восприятия пространственных сцен, пример с комнатой);

• 4)    формирование агентов-акторов;

• 5)    формализация входной информации о группе мобильных роботов (имя робота, показания датчиков);

• 6)    расчет основных характеристик робота: скорость, направление движения, функции изменения энергоресурса;

• 7)    построение модели группы роботов на основе расчетов;

• 8)    объединение модели множества задач и модели роботов в единую комплексную модель группы роботов, выполняющих комплексную задачу;

• 9)    расчет эффективности выполнения каждой из множества задач каждым из роботов.

Предложенная методика позволяет построить математическую модель робота на основе сенсорной информации в автоматическом режиме и учитывать взаимосвязь поставленных задач.

В дальнейшем планируется на основе разработанной методики построить математическую модель группы беспилотных летательных аппаратов, выполняющих комплексную задачу по патрулированию заданного участка местности, после чего разработать алгоритм группового управления роботами для решения комплексной задачи и далее провести анализ и оценить результативность и эффективность предложенных моделей и алгоритмов управления группой мобильных роботов.