Методика построения регрессионных моделей для оценки масс элементов космических аппаратов с использованием кластерного анализа

Существует несколько подходов к выбору основных проектных характеристик и формированию проектного облика космических аппаратов (КА) дистанционного зондирования Земли (ДЗЗ) - на основе: эвристического подхода; установки целевой аппаратуры и элементов обеспечивающих бортовых систем в корпусе заданных габаритов; совершенствования прототипов; совершенствования состава целевой аппаратуры в отсеке полезной нагрузки при неизменных характеристиках отсека служебных систем; компоновки КА «вокруг» оптико-элек-

тронного телескопического комплекса (ОЭТК); установки ОЭТК, высокоточных оптических приборов и чувствительных датчиков на термостабилизированной платформе; установки в состав КА нескольких типов целевой аппаратуры (ЦА) с ограничением общей массы и комплек-сированием работы этой аппаратуры; выбора основных проектных характеристик и начального облика по заданным целевым показателям эффективности.

При реализации упомянутых подходов к проектированию КА ДЗЗ необходимо безусловно выполнить целевые показатели, основными из которых являются периодичность наблюдения, линейное разрешение на местности (детальность), ширина полосы обзора, ширина полосы захвата, производительность съёмки, оперативность доставки видеоинформации на землю, срок активного существования.

Особого обсуждения заслуживает методический подход к проектированию КА ДЗЗ по заданным целевым показателям космической системы наблюдения. Ключом к реализации данного подхода является разработка математических моделей, связывающих целевые и проектные параметры КА, в частности, моделей для оценки массогабаритных, энергетических характеристик массозатратных элементов целевой аппаратуры и бортовых обеспечивающих систем (БС) КА ДЗЗ. Такие модели строятся на основе физических принципов работы тех или иных устройств, протекающих процессов или на основе обработки статистических данных по изделиям-аналогам с учётом передовых технологий или новых разработок.

Полученные значения массогабаритных, инерционных, энергетических и других проектных параметров КА обеспечивают реализацию устройств, с помощью которых осуществляется получение заданных целевых характеристик (без избытка или недостатка). Практически это означает, что осуществляется оптимизация основных проектных характеристик КА в неявной форме. Теоретически это означает, что производится оптимизация проектных характеристик без формализации задач математического программирования.

На ранних стадиях создания космических аппаратов (КА) весьма важна оценка их массогабаритных характеристик в зависимости от характеристик эффективности применения по целевому назначению. При этом в первую очередь необходимо построить модели для относительно больших по массе и габаритам систем и элементов КА. Для космических аппаратов высокодетального дистанционного зондирования земли (ДЗЗ) к числу таких систем, прежде всего, относится оптико-электронный телескопический комплекс (ОЭТК), масса которого может превышать 20% от массы КА (КА «Kompsat-2», «Ikonos-2», «KH-11», «GeoEye-1»,«OrbView-5»).

Методика построения регрессионных моделей с использованием кластерного анализа включает следующие этапы:

• -    сбор и анализ статистических данных по изделиям-аналогам;

• -    разбиение статистических данных на кластеры (достаточно однородные группы);

• -    построение регрессионных моделей (различного порядка для каждого кластера данных);

• -    анализ полученных результатов.

Рассмотрим эти этапы подробнее на примере построения регрессионной модели для оценки массы аппаратуры оптического наблюдения космических аппаратов дистанционного зондирования Земли.

СБОР И АНАЛИЗ СТАТИСТИЧЕСКИХ ДАННЫХ ПО ИЗДЕЛИЯМ-АНАЛОГАМ

Анализ характеристик ОЭТК показывает [1], что его длина в первом приближении пропор- циональна отношению H , а диаметр – от-R/ / AL ношению ba L, где, H - высота орбиты, AL – линейное разрешение на местности, B – ширина полосы захвата.

Поэтому масса ОЭТК m _{О ЭТК} является функцией указанных отношений: m О ЭТК = f ( H A L, B/ A L ) , где f ( • ) - неизвестна функция, подлежащая определению.

Статистические данные по КА ДЗЗ высокого и сверхвысокого разрешения и их оптико-электронной аппаратуре [2] приведены в табл. 1.

Анализ приведённых статистические данных показывает, что они являются весьма разнородными. Это объясняется тем, что в различной аппаратуре наблюдения могут использоваться разные целевые и конструкционные характеристики: диаметр апертуры, угловое разрешение, количество спектров наблюдения, высота полёта КА, оптические схемы, количество используемых зеркал, силовые схемы аппаратуры, конструкционные материалы и др. Существенное влияние на массогабаритные характеристики аппаратуры наблюдения оказывают такие факторы, как различные производители (технологическая культура производства), а также год выпуска аппаратуры.

Попытка построить регрессионную модель по всей их совокупности приведёт, очевидно, к низкому качеству такой модели. Поэтому необходимо предварительно разбить данные на более или менее однородные группы. Эта задача может быть решена с помощью метода кластерного анализа [3].

РАЗБИЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ НА КЛАСТЕРЫ

С помощью метода кластерного анализа можно произвести классификацию объектов, на которые влияет множество факторов, разбив эти объекты на заданное число компактных групп (кластеров). Мерой качества полученного разбиения является так называемое среднее внутрикластерное расстояние, которое показывает степень близости характеристик в рассматриваемой группе. Чем ближе рассматриваемые характеристики в группе (чем компактнее полученные кластеры), тем среднее внутрикластер-ное расстояние меньше.

Для каждого кластера определяется его центр – тот из объектов, сумма расстояний до которого от всех прочих объектов (внутрикла-стерное расстояние) является наименьшей.

Для получения адекватных результатов кластерного анализа исходные данные должны быть нормированы (например, относительно максимального или среднего значения). В противном случае параметры, значения которых

Таблица 1. Статистические данные по ОЭТК КА ДЗЗ

№ п/п.	КА	ОЭТК	H , км	A L , м	B , км	тОЭТК ,кг
1	GeoEye-1	GIS	770	0,460	16,4	452,0
2	КА-П	Лазурит	730	0,300	17,1	1541
3	WorldView-1	WV-60	496	0,460	17,6	380,0
4	Pleiades-1A	HiRI	705	0,700	20,0	195,0
5	Pleiades-1B	HiRI	694	0,700	20,0	195,0
6	Ikonos	OSA	686	0,820	11,3	171,0
7	CartoSat-2A	PAN	635	0,800	9,60	120,0
8	CartoSat-3	PAN (CartoSat-3)	630	0,300	6,00	120,0
9	Kompsat-1	EOS	685	6,60	17,0	35,00
10	Kompsat-2	MSC	685	1,00	15,0	150,0
11	Kompsat-3	AEISS	675	0,700	15,0	80,00
12	Kompsat-3A	AEISS-A	528	0,550	12,0	80,00
13	ASNARO	OPS	504	0,500	10,0	97,00
14	ALOS	AVNIR-2	692	10,0	70,0	198,0
15	ALOS	PRISM	692	2,50	70,0	528,0
16	FORMOSAT-2	RSI	891	2,00	24,0	114,0
17	Spot-5	HRG	832	2,50	60,0	356,0
18	GökTürk-2	EOS-C	684	2,50	20,0	41,00
19	CBERS-4	PANMUX	778	5,00	60,0	263,0
20	NigeriaSat-2	VHRI	718	2,50	20,0	41,00
21	VEN ^ S	VSSC	720	5,30	28,0	43,50
22	IRS-1C	PAN (IRS)	817	5,80	70,0	120,0
23	Аврора	Аврора	510	1,54	41,3	53,00
24	QuickBird	BGIS-2000	450	0,65	16,8	380,0
25	Deimos-2	HiRAIS	720	1,00	12,0	50,00
26	Ресурс-ДК	GEOTON-1	570	1,00	28,3	310,0

- Канберра:

существенно различаются, могут внести различный вклад в анализируемые данные и существенно повлиять на результаты анализа.

Измерение расстояний d y между т- мерными объектами x_t, X j предполагает введение метрики, т.е. способа измерения этого расстояния.

К числу наиболее часто используемых метрик относятся следующие:

- Евклидова:

m x^l - x^l d y = z

M X , + X j

Для получения более достоверных результатов анализа целесообразно использовать разные

метрики и сравнить получаемые результаты.

В настоящем исследовании будем считать,

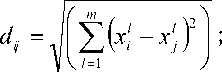
что функция отклика (масса ОТК) т ОЭТК в наибольшей степени зависит от двух переменных

(факторов) x =

H

/AL

^и y y = B A L •

-Манхеттеновская:

m dy =Z x- xlj\;

l = 1

Нормирование переменных, включаемых в

регрессионную модель ОЭТК, можно выполнить с помощью следующих выражений:

- Брея-Картиса:

x       ym x =---; y = -2—; m = —ОЭТК-, max          y max            ОЭТК™,,, max

d ij

m

Z|xi - xj l=1.

mm

Z xi +Z x l=1

где ^x max ^, У max ^, m O3TK max ^{- соответственно мак} симальные по рассматриваемой совокупности данных значения факторов x , У и массы ОЭТК.

Нормированные значения переменных приведены в последних трёх столбцах табл. 2.

Таблица 2 . Нормализованные статистические данные по ОЭТК КА ДЗЗ

№ п/п	КА	B x =-- A L	H у=тт AL	тоэтк , кг	x	y	m
1	GeoEye-1	35,65	1674	452,0	0,625	0,688	0,293
2	Лазурит	57,00	2433	1541	1,000	1,000	1,000
3	WorldView-1	38,26	1078	380,0	0,671	0,443	0,247
4	Pleiades-1A	28,57	1007	195,0	0,501	0,414	0,127
5	Pleiades-1B	28,57	991,4	195,0	0,501	0,407	0,127
6	Ikonos	13,78	836,6	171,0	0,242	0,344	0,111
7	CartoSat-2A	12,00	793,8	120,0	0,211	0,326	0,078
8	CartoSat-3	20,00	2100	120,0	0,351	0,863	0,078
9	Kompsat-1	2,576	103,8	35,00	0,045	0,043	0,023
10	Kompsat-2	15,00	685,0	150,0	0,263	0,282	0,097
11	Kompsat-3	21,43	964,2	80,00	0,376	0,396	0,052
12	Kompsat-3A	21,82	960,0	80,00	0,383	0,395	0,052
13	ASNARO	20,00	1008	97,00	0,351	0,414	0,063
14	ALOS	7,000	69,20	198,0	0,123	0,028	0,128
15	ALOS	28,00	276,8	528,0	0,491	0,114	0,343
16	FORMOSAT-2	12,00	445,5	114,0	0,211	0,183	0,074
17	Spot-5	24,00	332,8	356,0	0,421	0,137	0,231
18	GökTürk-2	8,000	273,6	41,00	0,140	0,112	0,027
19	CBERS-4	12,00	155,6	263,0	0,211	0,064	0,171
20	NigeriaSat-2	8,00	287,2	41,00	0,140	0,118	0,027
21	VEN p S	5,283	135,8	43,50	0,093	0,056	0,028
22	IRS-1C	12,07	140,9	120,0	0,212	0,058	0,078
23	Аврора	26,82	331,2	52,64	0,470	0,136	0,034
24	QuickBird	25,85	692,3	380,0	0,453	0,285	0,247
25	Deimos-2	12,00	720	50,00	0,211	0,296	0,032
26	Ресурс-ДК	28,30	570	310,0	0,496	0,234	0,201

Для выполнения кластерного анализа данных был использован статистический пакет STADIA отечественной разработки [4].

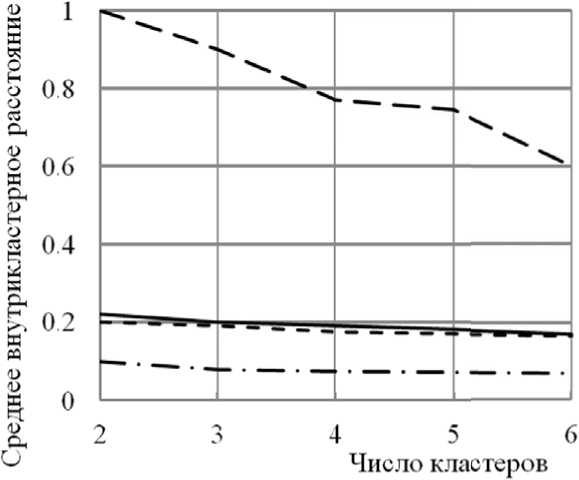
Измерение расстояний между объектами выполнялось с использованием 4 различных метрик: Эвклида, Манхеттеновской, Брея-Картиса и Канберра [4]. Число кластеров варьировалось в пределах от 2 до 6. Зависимость среднего внутрикластерного расстояния, рассчитанного в статистическом пакете STADIA, от фактического числа кластеров для различных использованных метрик показана на рис. 1.

Анализируя данные этого рисунка, можно видеть, что значение среднего внутрикластер-ного расстояния для трёх из четырёх использованных метрик практически перестает изменяться при достижении числом кластеров значения 5. Дальнейшее увеличение числа кластеров нецелесообразно, так как, с одной стороны, это практически не влияет на точность разбиения статистических данных, с другой стороны, увеличение числа кластеров сопровождается уменьшением числа содержащихся в них объектов, которое может оказаться недо- статочным для построения соответствующих регрессионных моделей. Так, например, двухфакторная модель второго порядка требует для своего построения не менее 6 наборов данных (значений факторов и отклика).

В целом, кластерный анализ позволяет лишь подготовить предварительные данные, а окончательное решение о разбиении статистических данных на кластеры принимает пользователь исходя из содержательных представлений о целях исследования.

В данной работе, исходя из полученных результатов, было принято решение о разбиении статистических данных на 5 кластеров. Однако фактическое число полученных кластеров при использовании метрики Эвклида ограничилось значением 3, а при использовании метрик ма-хеттеновской и Брея-Картиса – значением 4. Это объясняется тем, что при попытке дальнейшего увеличения числа кластеров изменение внутрикластерного расстояния оказывалось меньше погрешности расчета, установленной в пакете STADIA.

Ниже приведены соответствующие про-

Эвклид

— • - Манхеттен

---Брен-Картис--Канберра

Рис. 1. Зависимость среднего внутрикластерного расстояния от числа кластеров токолы расчёта в программе STADIA . Номера кластеров представлены в строках и обозначены цифрами 1, 2, 3 и т.д. После номера кластера в скобках представлены номера входящих в него объектов в соответствии с табл. 2, звёздочками помечены объекты, являющиеся центрами кластеров.

Метрика «Эвклид»

К л а с т е р ы:

Среднее внутрикластерное расстояние =0.1869

1= (1*,2,3,8)

2= (4,5,11,12,13,15,17,23,24,26*)

3= (6,7,9,10,14,16,18,19,20*,21,22,25)

Метрика «Манхеттен»

К л а с т е р ы:

Среднее внутрикластерное расстояние =0.07294

1= (1*,2,3)

2= (4,5,6,7,8,10,11,12,13*)

3= (15,17*,23,24,26)

4= (9,14,16,18*,19,20,21,22,25)

Метрика «Брей-Картис»

К л а с т е р ы:

Среднее внутрикластерное расстояние =0.1691

1= (1*,2,3,8)

2= (4,5,6,11*,12,13)

3= (15,17,23,24,26*)

4= (7,9,10,14,16*,18,19,20,21,22,25)

Метрика «Канберра»

К л а с т е р ы:

Среднее внутрикластерное расстояние =0.7459

1= (1,2*,8)

2= (3,6,7,10,15,17,23,24*,25,26)

3= (4*,5)

4= (11*,12,13)

5= (9,14,16,18,19*,20,21,22)

Можно видеть, что большинство используемых метрик позволяет выделить два устойчивых кластера: кластер, объединяющий объекты из табл. 2 с номерами 4, 5, 6, 11, 12, 13 (ОЭТК сверхвысокого разрешения) и кластер 2, объединяющий объекты с номерами 9, 14, 16, 18, 19, 20, 21, 22 (ОЭТК высокого разрешения с широкой полосой захвата). Эти кластеры включают число объектов, достаточное для последующего регрессионного анализа.

ПОСТРОЕНИЕ РЕГРЕССИОННЫХ МОДЕЛЕЙ

Построение регрессионных моделей, связывающих массу ОЭТК с целевыми характеристиками, было выполнено с помощью математического пакета Mathcad.

Ниже приводятся протоколы расчётов с соответствующими пояснениями.

Исходные данные для анализа представлены в табл. 3.

Таблица 3. Исходные данные для регрессионного анализа

Номер кластера	Номер объекта	Космический аппарат	B x =-- A L	H y = 77 A L	m O3TK ’ кг
1	4	Pleiades-1A	28,57	1007	195,0
	5	Pleiades-1B	28,57	991,4	195,0
	6	Ikonos	13,78	836,6	171,0
	11	Kompsat-3	21,42	964,3	80,0
	12	Kompsat-3A	21,81	960,0	80,0
	13	ASNARO	20,00	1008	97,0
2	9	Kompsat-1	2,57	103,8	35,0
	14	ALOS	7,00	69,20	198,0
	16	FORMOSAT-2	12,00	445,5	114,0
	18	GökTürk-2	8,00	273,6	41,0
	19	CBERS-4	12,00	155,6	263,0
	20	NigeriaSat-2	8,00	287,2	41,0
	21	VEN p S	5,28	135,9	43,5
	22	IRS-1C	12,06	140,9	120,0

Кластер данных для ОЭТК сверхвысокого разрешения

Задаётся, для удобства последующих вычислений, нумерация элементов матриц, начиная с единицы, для чего стандартной функции ORIGIN присваивается значение 1. Компонентам матрицы Mx присваиваются значения факторов x, y , компонентам вектора vy - значения отклика m_ОЭА :

ORIGIN := 1

	' 28.57 28.57 21.43	1007.14' 991.43 964.29		'195' 195 80
Mx :=	21.82	960	vy :=	80
	20	1008		97
	^ 13.78	836.59 ,		<171,

Задаётся порядок регрессии n : вначале принимается n = 1 (линейная регрессия), коэффициенты регрессии вычисляются с использованием стандартной функции regress и записываются в вектор z : .

Рассчитанные с помощью полученной модели значения отклика присваиваются компонентам вектора tvy:

;

.

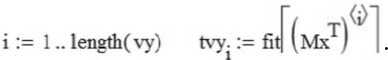
Как известно, регрессионная модель тем лучше соответствует статистическим данным, чем значение коэффициента детерминации ближе к единице; можно видеть, что качество данной регрессии невысоко. Действительно, сравнение фактических и предсказанных значений массы аппаратуры показывает их заметное различие, в особенности в области небольших масс:

	'195' 195 80		'170.087' 184.849 121.931
vy =	80	by =	130.792
	97		63.15
	J71>		< 147.19 ,

Для проверки адекватности полученной регрессионной модели вычисляется статистика Фишера Fis, как отношение дисперсии, обусловленной регрессией MSSR , к остаточной дисперсии MSSE ; для вычисления последних вначале рассчитываются соответствующие суммы квадратов разностей SSR и SSE и используются степени свободы dfr и dfe :

residual := vy - tvy SSE := X^ residual*

SSR := X' (tvy - mean(vy))* SSR = 9.205 x 10^

SSE 6.775 z 10*

dfr := 2 dfe := length(vy) - 1 - dfr dfe = 3

Для оценки качества полученной регрессии вычисляется коэффициент детерминации kd – квадрат коэффициента корреляции между фактическими и вычисленными (предсказанными) значениями отклика:

SSE msse := — dfe

. MSSR

Fis :=------

MSSE

SSR

MSSR :=--- dfr

Fis = 2.038

С помощью стандартной функции qF ( • ) вычисляется критическое значение статистики fc для уровня значимости p =0,05и соответствующих значений степеней свободы dfr и dfe :

.

То обстоятельство, что рассчитанное значение статистики Фишера меньше её критического значения (Fis < fc), заставляет признать построенную модель неадекватной имеющимся статистическим данным. Заметим, что модель регрессии может быть признанной адекватной лишь на уровне значимости 0,28, при котором соответствующее критическое значение статистики Фишера (2,005) становится меньше рас- считанного.

Для улучшения качества регрессионной модели повысим её порядок:

”-2 z л regress( Мхлу ,п )

fit(x) := interp(z,Mx,vy,x) i := 1.. length(vy)

by

Г/ T\® fit \Mx )

kd := corr(vy, tvy)* kd = 1

Коэффициент детерминации возрос до мак-

Таким образом, получена следующая регрессионная зависимость массы ОЭТК от целевых параметров:

m_03TK = 1,196 x ² + 1,868 ■ 10 ³ y ² - 0,042 xy

- 53,009 x - 2,537 y + 1782.                (1)

Проверка модели по критерию Фишера, ввиду полного совпадения фактических и предсказанных значений массы аппаратуры, не требуется.

Кластер данных для ОЭТК высокого разрешения

Построим вначале линейную модель:

ORIGIN := 1

Mx :=

' 12 445.5 4 114 ' 2.58 103.79 35 7 69.2 198 8 273.6 vy :- 41 12 155.6 263 8 287.2 41 5.28 135.85 43.5 , 12.07 140.86 ; v 120 ; симально возможного значения – единицы. Действительно, сравнение фактических и предсказанных значений массы аппаратуры показывает их полное совпадение:

n := 1 z := regress(Mx,vy,n) fit(x) := interp(z,Mx,vy,x)

	'195' 195 80		'195^ 195 80
vy =		tvy =
	80		80
	97		97
	J7R		J71,

i := 1.. length(vy)

2 kd := corr(vy,tvy)

residual := vy — tvy

tvy.

:= fit] I, Mx J

kd = 0.625

SSE := ^residual*

dfr := 2 dfe := length(vy) - 1 - dfr dfe = 5

Значения коэффициентов регрессии содержатся в векторе

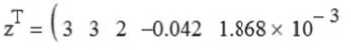
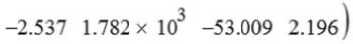
SSE

MSSE :=--- dfe

MSSR

Fis := -------

MSSE

SSR

MSSR :=--- dfr

Fis = 4.165

Первые две компоненты этого вектора представляют собой значения служебных переменных пакета Mathcad, третья – порядок регрессии, остальные – это коэффициенты при слагаемых в уравнении регрессии, соответствие с которыми указано в табл. 4.

Модель адекватна на уровне значимости 0,09 (ему соответствует критическое значение статистики Фишера fc , меньшее рассчитанного для полученной регрессии значения Fis ):

p := 0.09 fc := qF( 1 - p,dfr,dfe) fc = 4.05

Таблица 4. Значения коэффициентов регрессии

Компонента вектора z	z 4	z 5	z 6	z 7	z 8	z 9
Значение	- 0,042	1,868-10 -3	- 2,537	1,782-10 3	- 53,01	2,196
Член регрессии	xy	2 y	y	свободный член	x	x 2

После извлечения коэффициентов регрессии из вектора z уравнение модели можно записать в следующем виде:

m_03TK = 20,673 x - 0,423 y + 19,095. (2)

Полученная модель может быть использована для практических расчётов; однако можно попытаться получить более точную модель, повысив её порядок:

i := 1.. length( vy)

2 kd := corr(vy,tvy)”

tvy. := fit (mx^T)

residual := vy — tvy

SSE := ^residual”

dfr := 2 dfe := length! vy) — 1 — dfr dfe = 5

SSE

MSSE :=--- dfe

. MSSR

Fis :=------

SSR

MSSR := --- dfr

Fis = 8.795

p := 0.05 fc := qF( 1 - p,dfe,dfr) fc = 19.296

Поскольку выполняется соотношение Fis> fc, полученная модель адекватна на уровне значимости 0,05.

Извлекая из вектора у /                          — 3

z = 13 3 2 0.469 -6.032 x 10 -2.292 137.275 35.491 -5.09)

коэффициенты уравнения регрессии, можно записать его в следующем виде:

m_03TK = - 5,09 x ² - 6,032 • 10 ^{- 3} y ² + 0,469 xy

+ 35,491 x - 2,292 y + 137,275.

АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Кластерный анализ статистических данных позволил выделить два устойчивых кластера, достаточно обширных для построения на их основе регрессионных моделей.

В первый из них вошли шесть КА с аппаратурой сверхвысокого разрешения. Поскольку построенная для данного кластера регрессионная модель первого порядка показала низкое качество (коэффициент детерминации 0,576 и адекватность с уровнем значимости 0,29), было выполнено построение модели второго порядка (1), для которой коэффициент детерминации составил 1.

Для второго кластера, включающего восемь КА высокого разрешения с широкой полосой захвата, приемлемым качеством обладают как модель первого порядка (2) с коэффициентом детерминации 0,625 и адекватностью с уровнем значимости 0,09, так и модель второго порядка (3) с коэффициентом детерминации 0,779 и адекватностью с уровнем значимости 0,05.

Для прогнозирования массы ОЭТК с использованием регрессионной модели необходимо предварительно определить, какую из полученных моделей следует использовать. Это может быть сделано с помощью метода дискриминантного анализа [4].

Рассмотренная методика может использоваться для оценки масс различных бортовых систем космических аппаратов на ранних стадиях их создания, а также в общем для регрессионного анализа разнородных статистических данных.

ЗАКЛЮЧЕНИЕ

• 1.    Предложена методика построения регрессионных моделей на основе многомерных статистических данных. Показана возможность получения адекватных моделей в результате предварительного разделения разнородных данных на устойчивые группы методом кластерного анализа с последующим построением регрессионных моделей для каждой отдельной группы. Выполнено сравнение качества моделей различного порядка применительно к оптико-электронным телескопическим комплексам КА ДЗЗ.

• 2.    Регрессионные модели, получаемые с использованием предложенной методики, могут применяться на начальных этапах проектирования для прогнозирования массы бортовой аппаратуры космических аппаратов дистанционного зондирования Земли с заданными целевыми параметрами.