Методика построения структурно резервированной информационно-телекоммуникационной сети, реализующая триадный принцип ее построения

Анализ показывает, что оценка устойчивости информационно-телекоммуникационной сети (далее – ИТКС) не обеспечивает радикального изменения уровня устойчивого функционирования ИТКС в условиях воздействия противника, так как не изменяется ее структура. Более общим подходом к обеспечению устойчивости ИТКС является синтез структуры сети с требуемыми значениями показателей качества. Синтез – метод исследования явлений в их единстве и взаимосвязи. Это значит, что для решения задач синтеза необходимо обосновать совокупность методов, обеспечивающих решение подзадач синтеза больших систем [1; 4; 5].

Учитывая, что интенсивность обмена данными между узлами связи (далее – УС) сети не является однородной, в ИТКС можно выделить группы УС, интенсивнее связанные друг с другом информационными потоками. В этом случае увеличить производительность сети можно, разместив разные рабочие группы в отдельных ее сегментах. Сегментация сети может быть выполнена с использованием коммутаторов. В этом случае интенсивный информационный обмен, в том числе и широковещательный трафик, чаще выпол-

Методика построения структурно резервированной информационно- ...

Лукин Константин Игоревич

няется внутри одного сегмента, следовательно, интенсивность межсегментного трафика уменьшается, и количество коллизий в сети существенно снижается [12].

Методология реализации принципов устойчивости сети и триадный принцип

ее построения

Информационно-телекоммуникационная сеть относится к классу больших систем. Они не могут быть созданы за короткое время и предполагают фрагментарное (эволюционное) развитие. Поэтому одни ее элементы могут эксплуатироваться, другие – проектироваться, а третьи – исследоваться. По этой причине методология должна включать не только методы синтеза, алгоритмической и параметрической оптимизации (системное проектирование), но и методы инженерного проектирования (реализации результатов синтеза) [6].

С этой целью предлагается методологии реализации структурно-топологических принципов обеспечения устойчивости учитывать при построении ИТКС, включая методику построения структурно резервированной ИТКС, реализуя триадный принцип ее построения [7].

В результате вычисления порядковой функции графа, отражающего иерархическую структуру узлов связи ИТКС, получено их иерархическое распределение, определяющее опорную структуру системы. В рамках этой структуры ищется ее рациональный вариант [9]. Для определения группы УС ИТКС необходимо определить следующие отображения:

T 1

O ( X i ) ^ S ( m k : k = 1, S ) ; S < r ; S ( m k ) = ( m_u...,m s - 1 ,1 ) ;

X i ^ { X j : j = 1 m } ;

T 3

nj ^'jj, где отображение T1 определяет рациональное число S(mk) уровней иерархии структуры

ИТКС, здесь mk – число УС на каждом k-м уровне, k = 1,S; отображение Т2 определяет характер распределения УС, где j = 1,m ; отображение Т3 определяет множество зависимостей (Nnj) задач, решаемых j-м УС.

Критерии построения устойчивой информационно-телекоммуникационной сети

Рациональный вариант построения структуры ИТКС должен отвечать определенной системе критериев.

Для синтеза опорного варианта структуры ИТКС и разработки алгоритма ее корреляции с учетом применения противником средств и методов противодействия могут быть использованы следующие критерии:

• •    минимизация УС ( m );

• •    максимизация вероятности безошибочного и своевременного выполнения УС всего комплекса задач управления в соответствии с типовым вариантом функционирования ИТКС ( P );

• •    минимизация среднего времени решения оперативных задач УС в ИТКС;

• •    минимизация показателя равномерности загрузки между УС ( K _pk);

• •    минимизация общей стоимости содержания структуры ИТКС ( C ).

Первый показатель m в силу его прямой пропорциональной зависимости от стоимостных показателей структуры ИТКС является ее основной характеристикой.

S

Параметр m = 1 + ^ m , где m _k - число УС на k -м уровне иерархии структуры ИТКС

( k = 1, S , где S - число уровней структуры).

В соответствии с эргономическими требованиями к организации ИТКС эффектив ность уровня Р иерархии в структуре сети имеет ограничение снизу, то есть P > Pm^n .

Показатель Р в силу прямой корреляции с показателями устойчивости функционирования ИТКС также является основной эргономической характеристикой организационной структуры.

Связанным с данным показателем является показатель загруженности УС t , определяющий целевое предназначение сети. Ввиду жесткой корреляции показателя t c загру-

Методика построения структурно резервированной информационно- ...

женностью линий связи он также может рассматриваться как основная эргономическая характеристика ИТКС [11].

Показатель стоимости С зависит от затрат на закупку оборудования, его монтаж и содержание j -го УС k -го иерархического уровня структуры ИТКС, а также затрат на производство и эксплуатацию. Очевидно, что в процессе выбора рационального варианта структуры должно выполняться неравенство С <  C _min, где С _min – ограничения по стоимости.

Для расчета показателя стоимости может быть принято очевидное условие, что для каждого уровня иерархии структуры могут быть поставлены в соответствие определенные значения перечисленных выше затрат С _k. Тогда

S - 1

С = C + ^ m_kC_k ,                           (1)

k = 1

где С ₁ – затраты на закупку оборудования, монтаж, содержание, производство и эксплуатацию УСИТКС.

Показатель k _3k и k _pk взаимозависимы с показателем Р и являются вспомогательными. Поэтому при постановке задачи они должны учитываться при формировании ограничений [15].

Формулирование задачи построения ИТКС

Задача определения структуры и количества УС в ИТКС может быть сформулирована следующим образом.

Необходимо определить структуру S(mk), при которой обеспечивается minC = f1( S (mk )) и max P = f2( S (mk ), ё,м,ц (t), Q, e ,d ),            (2)

S ( m_k )                           S ( m_k )

где X, Ц , ф ( t ) - загруженность линий связи го отдельного УС, векторы загруженности линий связи и векторы времени обработки информации соответственно; векторы Q и е -соответствующие вероятности ошибочной передачи пакетов сообщений, определяемых функциональным предназначением УС и линий связи, резервируемых в соответствии с характером информационных потоков, определяемых матрицей 8 .

При этом выполняются ограничения на основные критериальные функции

Р>Р : ОС

min ; min и вспомогательные критерии

^K 3min <  ^K 3k <  ^K 3max , ^K pk <  ^K pmax , ^{TEUG k} = 1, ^-

Поставленная задача является двухпараметрической задачей векторной оптимизации с взаимопротивоположными критериями в факторном пространстве эффективность – стоимость. Ее общее решение может быть найдено на основе применения разнообразных методов скаляризации векторных критериев.

Прямая и обратная задачи оптимизации

Для определения значений нормирующих критериев стоимости и эффективности рассматриваются прямая и обратная задачи оптимизации [13].

Постановка первой (прямой) задачи сводится к следующему. Необходимо определить max P = f?(S ( mk ), Л,^ ,ф (t), Q, £ ,J)                                   (4)

S ( m_k )

при ограничениях на основные критериальные функции и вышерассмотренных ограничениях на вспомогательные функции.

Обратная задача формально может быть представлена как

S - 1

min C ^{( S (} m k ^{)) C} = C 1 + У m k C k

^{S (} m k )                       k = 1

при соответствующих ограничениях на основные критериальные и вспомогательные функции.

Ввиду существенной нелинейности критериальной функции Р ( • ) в задачах синтеза в первом приближении удобнее использовать параметр ( t ) суммарных потерь времени на решение оперативных задач. Тогда прямая задача синтеза будет иметь вид [17]

min t ( S ( m k )), ё ,м,ц ( t ) S ( m_k )

при условии выполнения ограничений на основные критериальные вспомогательные функции.

При этом критерии t ( • ), Р ( • ), следовательно, и решение задачи, находятся либо аналитически в условиях достаточно жестких ограничений, либо методом статистического моделирования в соответствии с моделью ИТКС, описание которой дано выше.

Рассмотрим один из вариантов аналитических расчетов структуры. Прямая и обратная задачи могут быть решены в рамках одной процедуры оптимизации, в процессе реализации которой фиксируются как первый, так и второй функционалы.

Примем следующие упрощающие предположения в отношении структуры ИТКС. Во-первых, будем предполагать, что иерархическая сеть структуры однородна, то есть характеристики загруженности УС одного и того же уровня иерархии одинаковы, и каждому УС данного уровня иерархии функционально подчинено одинаковое число потоков информации предыдущего уровня иерархии. Во-вторых, все потоки информации простейшие, длительности обслуживания информации на каждом УС и загруженность линий связи не ограничены, УС функционируют безотказно. Такие предпосылки в общем случае оправданы на стадии структурного проектирования ИТКС, когда проектировщик, в лучшем случае, имеет лишь средние значения интенсивностей оперативных задач и их обслуживания. Данный подход позволяет проектировщику осмыслить задачу, получить верхние оценки значений критериальных функций для различных вариантов построения ИТКС и провести предварительный отбор наиболее перспективных из них [10].

В качестве основного критерия выбора структуры ИТКС рассмотрим оценки значений временных характеристик обработки поступаемой информации [14]. Для этого определим средние потери времени в решении оперативных задач і- м УС k -го уровня иерархии:

tki   tcpki qk + tkk; ^i 1, mk, где qk – среднее число пакетов сообщений, находящихся в очереди УС k-го уровня иерархии; tcpki – среднее время обработки пакетов сообщений УС k-го уровня иерархии; tkк – среднее время согласования (координации) информационных потоков УС k-го уровня иерархии со стороны УС смены вышестоящего уровня.

Для однородной структуры ИТКС общий критерий, отражающий временные потери для k -го уровня иерархии это

*(Ю = mk-i tk-i + tk, где mk– число УС на k-м уровне иерархии; tk–1 – соответствующие потери пакетов сообщений для УС (k – 1)-го уровня; tk – потери пакетов сообщений одного УС k-го уровня.

Методика построения структурно резервированной информационно- ...

Тогда с учетом однородности структуры количественное выражение общих за всю структуру временных потерь

S

• = ^ t ki m k , m s = ¹ •

^k = 1

Если сеть однородна, то интенсивность входящего простейшего информационного потока для любого УС k-го уровня иерархии k-1

^ = —П q k , m

k j = 1

где Л - интенсивность суммарного информационного потока ИТКС; g _k - степень интеграции пакетов сообщений на k -м уровне иерархии.

Степень интеграции пакетов сообщений зависит от сложности ИТКС на k -м уровне. Чем больше различных источников пакетов сообщений составляют основу информационного потока, тем более сложным он является [3]. Исходя из изложенного, предположим следующий закон изменения коэффициента g _k:

gk (mk) = exp(ak (mk -|NkI)),mk ={1,2,3^} ,                  (11)

где _k – интенсивность изменения коэффициента интеграции информации на k -м уровне иерархии ИТКС; g _{k = 0} = 1 при m _k> | N _k|.

Тогда в силу (10), (11) имеем

S

•=Z

k = 1

k - 1

Л П g .

j = 1

A

k - 1

\ + t kK

M k M k m k ^-ЛП g j

I I              j = 1

/

.

Отсюда несложными преобразованиями получим систему уравнений относительно оптимальных значений m *: k r k-1   ?

Л П g j

M k

r           k - 1 у

M k m k ^-ЛП g j

= t k , ( k = 1, 5 - 1 ) .

Ее решением является рекуррентное соотношение k-1

(

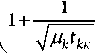
mk = - ЛП gj

M k   j = 1

позволяющее последовательно вычислить все значения m _k ^* – от m _{S – 1}^*до m ₁^*. Полученные значения m округляются до ближайших целых чисел, а возможная неоднозначность решения устраняется непосредственным расчетом по формуле (12) [16].

Если положить, что время координации действий узлов связи и актуализации их информации на последующем уровне организации пропорционально интенсивности решения оперативных задач номерам узлов связи вышестоящего уровня иерархии, то есть tkk « ~, YS" = 0,

M k + 1

то тем же методом можно найти оптимальные значения:

k - 1

ЛП gj

*

Mk =

j = 1

2 m_k

.

Выражение (14) позволяет при известных m _k и S _k путем рекуррентных вычислений определить требуемый уровень доступности информации на каждом иерархическом уровне [2].

Отношение стоимости и временных характеристик будет соответствовать времени прохождения информации от нижнего ( k = 1) до верхнего ( k = S ) уровня иерархии ИТКС:

S

ton = У tki ( S (mk )) • k=1

При условии наличия ограничений на суммарные стоимостные затраты задача определения структуры ИТКС (прямая задача оптимизации) будет иметь вид

S min У tki ( S, mkЛ, Mk , tkn )                               (15)

m v m 2,..., ms-1 “ при условии

У C_A <  C _do„ ,                          (16)

k = 1

где C _доп – допустимые затраты на организацию и поддержку устойчивого функционирования ИТКС; C _k – стоимость организации и поддержки функционирования УС k -го уровня иерархии ИТКС.

Для решения задачи вида (15) используется метод неопределенных множителей Лагранжа [18].

Опуская дальнейшие выкладки, окончательно решение задачи в форме рекуррентного выражения может быть представлено следующим образом:

*

m k =--⁺--

M k    M k'

^C don ] ²

I ,

где p k* - задаваемый уровень нагрузки УС информационными потоками.

Как видно из формулы (17), стоимостные ограничения оказывают существенное влияние на структуру ИТКС. В отношении вида функций Μk(Ck) может быть принята либо аппроксимация вида fc(Q) = актахехр(С1 /Ск\либок^Ск) =к, где Μkmax, а – параметры аппроксимации зависимости Μk(Ck).

Параметр Μ_kmax определяет предельные значения загруженности линий связи (элементов) на данном УС при данном распределении информационных потоков и характере решаемых задач на УС. Уровень Μ_kmax(Μ_k ) зависит от конструктивных, организационных и технических характеристик ИТКС [19].

При этом условно можно принять С _k = aC ₁, где С ₁ – стоимость одного УС первого уровня иерархии; a – коэффициент пропорциональности, отражающий рост стоимости УС вышележащих уровней иерархии ИТКС.

Методика построения структурно резервированной информационно- ...

Заключение

Таким образом, структуру ИТКС следует рассматривать как опорный вариант, служащий основой для принятия решения о целесообразности или нецелесообразности дальнейшей ее трансформации на основе динамики изменения информационных потоков при воздействии противника [8].