Методика повышения качества изделий электронной техники на различных стадиях производства

Технологический процесс (ТП) изготовления интегральных микросхем (ИМС) является многофакторным объектом со сложной структурой внутренних взаимосвязей. Рост степени интеграции компонентов и их функциональной сложности обуславливает появление новых острых проблем в области повышения качества и надежности изделий микроэлектроники. Так, значительное увеличение выпуска ИМС тормозится сравнительно низким процентом выхода годных. Причиной этого является несовершенство как самой технологии изготовления микросхем, так и методов и средств их контроля и управления. В статье рассматривается методика исследования ТП производства кристаллов ИМС с целью повышения качества изделий электронной техники непосредственно в производственных условиях.

• 1.    Методы исследований. В силу сто-хастичности ТП и вероятностного характера контролируемых величин в условиях массового производства ИМС наиболее перспективным для решения указанных задач является математико-статистическое направление причинно-следственного подхода. Объект при этом рассматривается как некоторая система взаимодействия входных параметров с некоторой выходной целевой функцией, причем структура и степень взаимосвязи параметров в общем случае не известны (модель «черного ящика»). Результатом реализации этого подхода является получение на основе экспериментальных данных математических моделей процессов в виде регрессионных уравнений,

• 2.    Результаты исследований. Исследования проводились в несколько этапов. Охватить весь технологический процесс изготовления ИМС в целом является практически невыполнимой задачей. Поэтому на первом этапе мы ограничились лишь частью сложной производственной цепи, на выходе которой имелся самый большой процент брака, а именно ТП формирования структуры ИМС на уровне кристаллов. Этот процесс состоит из множества операций, на которых действуют десятки факторов различной физической природы и различного характера проявления (вероятностные, случайные, детерминированные и т.д.), со сложной многоуровневой структурой взаимосвязей. В качестве целевой функции можно выбирать различные параметры ТП в зависимости от цели и уровня исследований. Главное, чтобы параметр являлся комплексным выходным показателем качества (ВПК) на данном уровне. Например, это может быть процент выхода годных всего ТП или отдельных его операций. В рассматриваемом

описывающих механизм взаимодействия входных и выходных параметров. Получаемые математические модели используются как для диагностики состояния объектов, так и для прогнозирования их поведения, выявления тенденций и скорости изменения и развития. В электронной промышленности накоплен определенный опыт использования этого подхода, однако слабым звеном является моделирование в условиях непрерывного производственного цикла, которое учитывало бы специфику сбора данных, а также структурные особенности и сложность исследуемых объектов.

Как известно, эксперимент может быть специально спланирован, его называют активным, а может быть лишь пассивным измерением значений факторов при различных состояниях объекта (пассивный эксперимент). В последнем случае получение информации не требует больших затрат на проведения опытов, т.к. осуществляется в непрерывном производственном цикле, хотя и занимает больше времени. Одним из самых распространенных и давно известных методов расчета регрессионных моделей в условиях пассивной информации является классический метод наименьших квадратов (МНКК) [1, с.141]. Однако он обладает рядом свойств, ограничивающим его применение в технологических процессах изготовления ИМС. Как известно, свойства информации, полученной при реализации пассивного эксперимента, отличаются от свойств активного плана, что сказывается, в конечном итоге, на точности и эффективности рассчитанной математической модели. Так, нарушение свойств ортогональности, линейной независимости, нормировки столбцов исходной таблицы данных приводит к тому, что коэффициенты будущей модели являются смешанными оценками, и любое изменение формы уравнения требует пересчета всех коэффициентов заново. Кроме того, невозможна процедура статистической проверки адекватности таких моделей (например, по критерию Фишера), нет информации о степени влияния каждого фактора на целевую функцию, имеются определенные неудобства вычислительной процедуры при возрастании числа исследуемых факторов. Все это снижает точность расчетов и ограничивает возможность применения метода непосредственно в производственных условиях, т.к. снижается оперативность обработки информации.

Проблему получения адекватных математических моделей с выявлением степени влияния на целевую функцию каждого рассматриваемого фактора в отдельности, предлагается решать с помощью специального метода – метода наименьших квадратов с предварительной ортогонализацией исходных данных (МНКО) [ 2, с.274 ] . В отличие от классического метод МНКО предусматривает процедуру предварительной ортогонализации исходных данных, что позволяет определить независимые оценки коэффициентов регрессии со всеми необходимыми процедурами статистического анализа (проверка на значимость, однородность, адекватность). Это обстоятельство и обеспечивает высокую точность, разрешающую способность и эффективность метода в условиях реального производства массовой продукции.

исследовании в качестве ВПК было выбрано выходное напряжение логического нуля, являющееся комплексной оценкой как самого ТП, так и его продукции. Кроме того, именно по этому параметру имелся наибольший процент брака на выходе.

Главная сложность в исследовании подобных процессов состоит в, так называемом, «проклятии размерности пространства». Дело в том, что на сегодняшний день не существует эффективных методом получения математических моделей объектов, в которых действуют десятки, а то и сотни входных факторов. А процесс производства ИМС, как отмечалось выше, именно таковым и является. Поэтому на следующем этапе необходимо сократить исходный список входных факторов, оставив в нем лишь сильнодействующие. С этой целью была построена структурная схема формирования ВПК, исходя из процесса формирования основных технических свойств изделий, а также технологических этапов изготовления пассивных и активных элементов на кристалле. На нижнем уровне иерархической схемы располагались технологические факторы процесса (температуры, расходы газов, длительности процессов и т.д.), на следующем уровне – электрофизические параметры (ЭФП) структуры микросхем (поверхностные сопротивления слоев, их физические размеры и пр.), затем следовали ЭФП компонентов ИМС (коэффициенты усиления, входные и выходные напряжения диодов Шоттки, сопротивление тела коллектора и др.). На самом верхнем уровне иерархии находились статпа-раметры – выходное напряжение логического нуля и логической единицы, выбранные в качестве ВПК кристаллов ИМС. При этом учитывалась возможность измерения и контроля рассматриваемых факторов и параметров на конкретном производстве.

Построение структурной схемы значительно уменьшило неопределенность в идентификации взаимосвязей параметров, однако, эти связи могут быть еще достаточно сложными (пересекающимися, обратными и т.д.), что затрудняет дальнейшее моделирование. В этом случае целесообразно воспользоваться подходом, связанным с агрегированием параметров, т.е. выделением группы факторов в виде одного обобщенного фактора. Реализует этот подход так называемый метод корреляционных плеяд [3, с.96], основанный на предположении, что измеряемые параметры наиболее сильно коррелируют друг с другом в том случае, когда они сильно зависят от одно- го и того же фактора. Приняв это предположение за исходную гипотезу, строится разбиение всех измеряемых параметров на такие группы – плеяды, что параметры, принадлежащие одной группе, в некотором смысле сильно коррелируют между собой, а параметры, принадлежащие разным группам, коррелированны относительно слабо. При этом матрица корреляций преобразуется в некоторый граф с учетом возрастания коэффициентов корреляции между параметрами. Фрагмент такого графа с 7 плеядами представлен на рис.1. Всего было рассмотрено 58 параметров, из которых после разбиения получилось 12 плеяд.

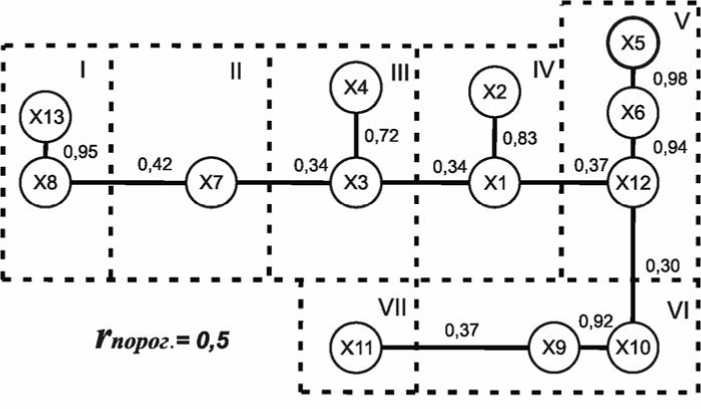
Рис. 1. Фрагмент графа корреляционных плеяд

При выборе порогового значения коэффициента корреляции при разбиении необходимо учитывать как статистический, так и физический смысл исследуемой взаимосвязи. Отобрав от каждой плеяды по одному (возможно два) представителя, получаем список информативных параметров, которые в дальнейшем войдут в математическую модель. На этом этап сокращения факторного пространства завершен.

Следующим этапом исследования является определение математической модели зависимости ВПК от параметров, выявленных на предыдущем этапе. Методом МНКО были получены модели, одна из которых имеет следующий вид:

Uвых(0) = 419,7 + 5,365 X11 + 1,970 X5 + 1,394 +X1 – 0,55X7 + 0,020 X4 , где: Uвых(0) – выходное напряжение логического нуля; X1 – поверхностное сопротивление скрытого слоя; Х4 – статический коэффициент усиления транзистора; Х5 – поверхностное сопротивление эмиттера; Х7 – выходное напряжение диода Шоттки на кристалле; Х11 – сопротивление на кристалле.

При этом были соблюдены все фор- мальные процедуры статистического анализа, в том числе проверка на значимость коэффициентов модели и ее адекватности. В модель вошли лишь сильнодействующие факторы, выявленные по критерию Стьюдента [4, с.331]. Но это не означает, что остальные факторы, не вошедшие в модель, не влияют на целевую функцию. Просто их влияние гораздо слабее на фоне оставшихся факторов, поэтому с риском 1-5% им можно пренебречь. По полученной модели можно прогнозировать поведение Uвых(0) в зависимости от изменения значений входных факторов путем подстановки в уравнение конкретных значений Хi. Причем достоинством уравнений данного типа является то, что значения факторов подставляются в натуральных единицах измерения, без каких либо преобразований, что очень удобно в условиях реального производства. Кроме того, с помощью уравнения решается и обратная задача по определению величин факторов Хi для получения требуемого значения целевой функции.

Представленная выше модель описывает взаимосвязь параметров верхних уровней иерархии. Вошедшие в нее параметры, в свою очередь, формируются составляющими нижнего уровня, т.е. факторами технологических режимов. Для этих параметров также были рассчитаны математические модели, описывающие влияние разброса технологических режимов различных операций на параметры микросхем на кристалле. Путем корректировки параметров режимов (в пределах допустимых значений) по модели можно скорректировать качество готовой продукции, т.е. увеличить количество микросхем с требуемыми характеристиками.

Аналогичные исследования следует проводить на различных уровнях формирования ВПК (согласно структурной схеме). При этом на одном уровне иерархии параметр может выступать в качестве целевой функции, а на другом – в качестве входного фактора. Таким образом, можно скорректировать все «узкие места» сложного многофакторного процесса.

Выводы: приведенные методы и результаты исследований показывают, насколько эффективно можно применять современные методы научных исследований в условиях сложных многофакторных процессов, каким является ТП изготовления ИМС. В настоящее время такой подход, на наш взгляд, является единственным эффективным средством изучения одновременного влияния всех факторов, как сильно, так и слабодействующих на выходной показатель качества продукции. По полученным математическим моделям можно сделать выводы относительно источников появления изделий низкого качества, давать рекомендации по оптимизации технологических режимов конкретных опера- ций непосредственно в производственных условиях. Внедрение полученных результатов позволяет увеличить выход годных изделий. Следует также отметить, что математические модели данного типа справедливы лишь для тех процессов, в условиях которых ставились эксперименты по их определению. Поэтому в случае каких-либо изменений в конструкции изделий или технологии их изготовления математические модели следует корректировать, проводить дополнительные эксперименты и заново рассчитывать коэффициенты моделей. Данная методика исследований реализована в виде пакета прикладных программ, позволяющего оперативно, в условиях реального производства производить необходимые расчеты по результатам контрольных измерений в ходе технологического процесса.