Методика повышения точности увязки размеров в агрегатно-сборочном производстве летательных аппаратов с использованием аппарата теории размерных цепей

лым рядом таких факторов, как несовершенство методики формирования требований к точности изготовления ЛА и точности увязки конструктивных размеров, которые обеспечивают заданное качество, но не должны быть завышенными, так как в этом случае не обеспечивается выполнение требований экономичности производства. Установление оптимальных соотношений между этими противоречивыми требованиями к производству самолетов может быть найдено из анализа и оценки основных факторов, оказывающих, с одной стороны, влияние на выполнение конечной точности изделия, а с другой – на затраты производства и эксплуатации.

Комплексное развитие систем САПР ТП для конструкторско-технологической отработки изделий на базе современных информационных технологий весьма сложны и специфичны, а математическая модель включает математическое описание связей между основными переменными и ограничения, накладываемые на область их изменения. Также математические модели должны соответствовать установленным стандартам CALS-технологий и обеспечивать достаточную точность и взаимозаменяемость при выполнении следующих условий и принципов:

• -    возможности функциональной и структурной декомпозиции;

• - вариативности задания граничных условий для конкретных условий производства;

• -    системности, последовательности и связности;

• -    многоуровневому принципу построения, от-ражаю-щему иерархию комплекса требований на соответствие технологических операций условиям производства, возможности их агрегирования

по группам и логическим компонентам, необходимым для реализации этих групп в виде упорядоченного набора функциональных модулей как компонент сборки.

На уровне граничных условий для объекта сборки задаются исходные параметры технологических процессов из информационной базы САПР ТП, включающие сведения о точности и состоянии технологического маршрута по параметрам размерных цепей в заданной точке. Координаты точек на плоскости известны из содержания электронной модели сборки. Обозначим R i = ( r i1 , r _i2 .., r ij ) - множество точек технологического маршрута i-ого узла, где каждый радиус -вектор r ij = r ij ( x 1 , x ₂ , x ₃ , t ) соответствует расчетной точке x 1 ,x ₂ ,..., x .как координате точки в размерной цепи технологического маршрута в плоскости или пространстве; t – время обработки расчётной точки. Участком заданной траектории сборки агрегата является отрезок между точками r ij и r ij _{+ 1} . Далее для упрощения изложения будем называть его участком размерной цепи технологического маршрута узла. Положение i-ого узла в пространстве Е в k-й момент времени характеризуется точкой f k ( x 1 _k , x _{2 k} , x _{3 k} , t_k ), образованный парой S ₀ =< S ₀ вх , S ₀ вых >  таким образом, что устанавливается соответствие между S _{0 в}х и некоторой точкой f производственного пространства с координатами ^fex = ^(min( x 1 ^),min( x 2 ^),min( x 3» и между ^S 0 вых ^и f_вых = (min( x , ),min( x ₂),min( x ₃)), где min(...), max(...) – соответственно наименьшее и наибольшее из значений координат точек данного участка сборки в пространстве Е.

Любой точке fk (x1 k, x2k, x3k, tk ), однозначно соответствует некоторая точка s в начальном базисе M(q) в разных вариантах построения размерных цепей. С учетом сделанных допущений о характере технологического маршрута представлением сборки i-ого узла в точке rij является последовательность векторов S(Ai) = (S“Pv(p) |(p)e (Pi)) ^ Ri, в которой выход предыдущего вектора совпадает с входом последующего. Для систематизации точек размерных цепей введем обозначение (pi) С (P) для множество индексов векторов звеньев i-го узла. Для каждого вектора этой последовательности должно выполняться условие: S "Pv(p) « rij e Ri, в силу которого S“£v(p) есть вектор, определяемый парами точек размерной цепи по заданной траектории сборки до выхода на замыкающее звено. Тогда из аксиомы о физической интерпретации точек размерной цепи в любой момент времени tk путём линейных преобразований с построением матриц операторов преобразований сборочного пространства можно определить координаты точки s для формаль- ного представления текущей точки размерной цепи для сборки во всех интерпретациях компоновок размерных цепей, начиная с опорного базиса, что соответствует уравнениям движения в операциях сопряжения элементов сборки узла по участку от rij к rij+1:

x 1 _k = r ij + dtW sin K ;

x₂, = ri + dtW cos K ;                    (1)

• 2 k ij

• ^x 3 k = r ij ^{+ dtV}y , где W, V_y , K - параметры сборочного пространства агрегата. Текущий угол траектории участка размерной цепи К определяется схемой технологического маршрута. Соответственно:

dt = t_k - 1 ( r j ),dt ^ p ( S "⁽ t ^{)( p} ) , s “ ⁽ t ⁾⁽⁰⁾ ). (2)

Представим согласно (1) участок вектора S«(3^{v (0)} таким образом, что

^ ₍ S « (WM⁰⁾ , S « <²⁾< ^v x⁰⁾ ) = 1 ^ E ^v ) . (3) Тогда, если известны координаты точки размерной цепи как точки s “ ⁽ t ⁾⁽⁰⁾ в опорном базисе, то можно определить координаты вектора X = ( x 1 , x ₂) T как координаты точки f k в пространстве сборки:

X = dX + BX _M , где dX = ( dx 1 ,dx ₂) T - вектор приращений по осям координат участка размерной цепи маршрута; В – матрица перехода из частной системы координат участка технологического маршрута в общую систему координат сборки, определяемая следующим образом:

B =

(srn, K)        cos(180 - K) ^

(- cos(180 - K )sin K       )

XM = (22v)Ep(v)^v)e{x,y})T.

Д , X ₂ - координаты точки s в опорном базисе, причём Х ₂ = 1 — Х 1 и Х ₁ + Х ₂ >  1 .

Такой подход позволяет использовать инвариантные способы расчёта параметров технологических цепей, разработки оптимальных программ функционирования технологических процессов и представления в локальном базисе j-го участка маршрута i-го узла или отдельной детали как интегрального вектора событий или множества таких векторов в пределах конфигурации сборочного пространства.

Преимуществом введённой интерпретации размерных связей технологического маршрута является исключение дополнительных преобразований при расчёте параметров отдельных звеньев за счёт того, что интегральный вектор по входящим звеньям W всегда однозначно ориентируется относительно опорного базиса независимо от значений параметров линейных и угловых перемещений сопрягаемых базисных точек с учётом конструктивно-технологических и нормативных требований к объектам сборки.

Таким образом, для того чтобы обеспечить высокую точность увязки размеров, необходимо все этапы, дающие большие погрешности в каждой из индивидуальных ветвей, перенести в общие для обоих размеров этапы. В этом случае погрешность увязки будет меньше погрешности каждого из размеров.

Следовательно, процессы определения области рассеивания пространственной размерной цепи для сопрягаемых поверхностей деталей, входящих в сборочную единицу, сопрягаемых по точкам, линиям или поверхностям, можно представить как множество последовательно перемещаемых точек с дискретным положением радиус – векторов траекторий адекватных размерных цепей, или некоторых линий в пространстве. Образующие размерные цепи линии, представляющие собой траектории движения точки на плоскости или в пространстве, могут быть прямыми или ломаными. Для определения положения сопрягаемой поверхности относительно какой-либо другой поверхности или относительно системы координат рассмотрим расположение системы точек, образующих линии в пространстве, которые формируют поверхность сопряжения по условиям однозначного задания положение этой поверхности в пространстве относительно выбранной системы координат. Также необходимо задать положение какой-либо точки данной поверхности относительно системы координат и функции, определяющей образование линий и поверхностей, проходящих через данную точку.

Рассмотрим пространственную размерную цепь (рис. 1), определяющую положение конца вектора последнего составляющего звена В _l относительно начала вектора В₁ первого звена цепи. Составляющие звенья размерной цепи A, Ап ,… A являются векторными величинами r_ij, которые определяются в системе координат параметрами компонент каждой составляющей звена цепи. Параметры размерной цепи определяют величину (модуль) вектора и его положение в пространстве. Количество параметров, определяющих вектор в системе координат, должно быть минимально необходимым и достаточным. Вектор В _i в декартовой системе координат X₀, Y₀, Z₀ зададим координатами x_i , y_i , z_i , значением длины радиуса вектора и углового положения его относительно координат или различными сочетаниями этих параметров. Тогда положения составляющих звеньев размерной цепи А₁,А₂,…,А _l , относительно исходной системы координат X₀, Y₀, Z₀ определяются параметрами каждого звена и параметрами, показывающими положение координатных систем со-ставляющих векторов относительно друг друга. При этом составляющие звенья размерной пространственной цепи обра-

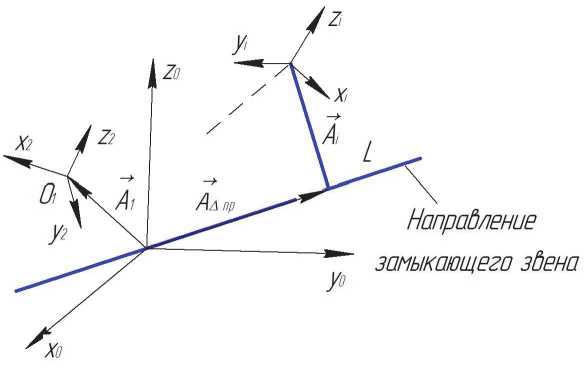
Рис 1. Последовательность построения пространственной векторной размерной цепи по условиям сборки зуют вектор замыкающего звена АДк, который определяет положение конца последнего сос-тав-ляющего звена цепи относительно начала первого звена. Положение вектора замыкающего звена в пространстве определится проекцией линии L (рис.1) на направление замыкающего звена в исходной системе координат X0, Y0, Z0. Проекция имеет определенные конкретные параметры. При рассмотрении влияния одного из составляющих звеньев размерной цепи на величину замыкающего звена А”к можно видеть, что величина замыкающего звена увеличивается или уменьшается в зависимости от направления составляющих звеньев по отношению к замыкающему на величину проекции этого звена на замыкающее звено в базовой системе координат. Следовательно, номинальный размер замыкающего звена можно определить по формуле:

;

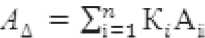
здесь Кi – передаточное отношение звена цепи; n— число составляющих звеньев размерной цепи.

Для моделирования реальной системы АСП необходимо дополнить методику в части возможности учёта случайных величин, которые выполняются в определенных ранее заданных интервалах (допусках). В связи с этим положение конца вектора В_i последнего звена цепи будет находиться в некоторой пространственной области, которая в пространстве сборки будет определяться конической фигурой, в основании которой лежит область рассеивания конца суммарного вектора в пространстве. Вершина конической фигуры находится в начале исходных координат. Образующие конической фигуры представляют собой предельные положения линий, определяющих фактическое направление замыкающего звена. Для определения области рассеивания замыкающего звена необходимо определить ее проекцию на направление замыкающего звена, что позволит получать конкретные значения размеров замыкающих звеньев с учетом номинальных размеров составляющих звеньев и допусков на них.

Например, при обработке корневой нервюры кессона отъёмной части крыла для стыковки с корневой нервюрой центроплана нас будет интересовать расстояние между центрами базовых и рядовых отверстий разъёма. Для построения размерных связей необходимо определить расстояние А”к между двумя точками O1 и О2(рис. 2), представленными соответствующими проекциями Ах1, А y1 и Аz1 и Ах2, А y2, Аz2 в осях координат Ox, Оу, Oz с началом отсчета в точке О. Составляющими параметрами размерной цепи являются размеры, определяющие расстояние между проекциями сопрягаемых точек на оси Ох, Оу, Oz в системе координат XYZ. Для расчета величины искомого расстояния A”к1-2 звена А1 – А2 пространственной размерной цепи получим:

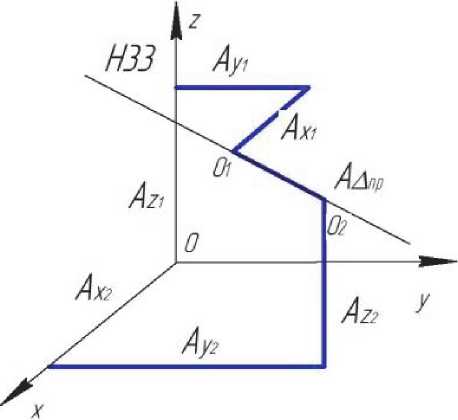
Рис. 2. Схема определения области рассеивания замыкающего звена A_”пр пространственной размерной цепи

Адк1-2 = J (^ - ^Л^ + (Ayl - Ayz)² + (Ad - AJ². (5)

Составляющие параметры этой цепи выпол-

няются с заданными допусками и могут иметь как наибольшие, так и наименьшие предельные значения. Поле рассеивания замыкающего звена представляет собой разность между наибольшим

и наименьшим его предельными значениями:

юАд =         — .-._....         (6)

Подставив в (5) значения (А_max – А_min) вместо (А₁- А₂), учитывая значения задаваемых в граничных условиях величин А _{Д пртах} и A _{Д прmin}, определим с использованием теории размерных цепей

циклов. Каждому простому циклу, включающему в себя замыкающее звено размерной цепи, соответствует алгебраическое уравнение простой размерной цепи, а число таких уравнений при сложной структуре размерных связей равно числу простых циклов в графе размеров. Тогда условие рассеивания выполняется, если

A

x 1 min

= A

x 2max

A

y 1 min

= A

y 2max

величину поля рассеивания:

т А.= V -

–

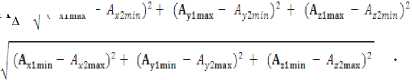
Анализ уравнения (7) показывает, что поле

A

z 1 min

= A

z 2max

Тогда поле рассеивания замыкающего звена (8) определяется:

рассеивания замыкающего звена зависит от полей рассеивания составляющих пара-метров, а также от величин размеров этих звеньев, т. е.

- А = f ( А х1 ^,А х2 ,-А;

А y1 ,А y2 ,…,А yj ; А z1 ,А z2 ,…,А zk ). (8)

Рассмотрим случай, когда при расчете пространственных размерных цепей необходимо обеспечивать минимальное значение величины

^ ^A D _n p ^⁽ A xlmax A x 2min ^{+ (} A ylmax A y 2min ) ^{+ (} A z Imax A z 2min ) ^{0 (10)}

Значения , и в уравнении (9) можно представить в следующем виде:

А ,    =А „ . +T, x1 max      x 2 min     x1

замыкающего звена цепи, в том числе равное нулю (замыкающее звено как зазор в соединении трубопровода со штуцером агрегата, где минимальный зазор должен быть равным нулю, и др.):

A y Imax    A y 2min ^{+ T} y 1              (11)

z1 max       z 2 min      z1 , где Tx1, Ty1, Tz1 — допуски на размеры Ax1, Ay1, Az1.

Аналогично получим:

A

Д пр min

= ( A x

A

2max

) 2 + ( A ^y

A y 2max

. )² + ( A z

A z 2max

. )² = 0

Для автоматизации процессов расчета размерных связей в этом случае размерные цепи можно представить как графы размеров, где про-

А ,    = А , . +T, x 2 max      x 2 min x 2

y 2max       y 2min ⁺ T y 2

z 2max z 2min ⁺ T z 2

стым размерным цепям соответствуют простые

где Tx2, Ty2, Tz2 — допуски на размеры Ax2, Ay2, Az2. Заменив в (12) величины Ax2max, Ay2max, Az2max их значениями по (9), имеем:

циклы, вершинами являются поверхности, линии и точки, соединяемые размерами, а сами размеры – ребрами. При связанной размерной цепи граф размеров содержит не менее двух простых

A

x 2 min

y 2 min

А , .

z 2min

A, - T„ x1 min     x 2

= А . .

y 1min

-

т.

y 2

Д -Т - z1 min      z 2

Подставив значения (13) в (10) и произведя преобразования по условиям Л _д пр min = 0 найдем: М =_л/ (Т. - Т ) 2 + (Т. - Т ,)² + (Т. - Т ,)² (14)

Д пр    у V   x 1      x 2/     v   y 1      y 2/      z  z 1      z 2 A  v '

Формулу (14) можно представить в общем виде для любого числа составляющих звеньев, заданных координатным способом при условии, что координаты составляющих векторов параллельны друг другу:

nnn

^ д пр = . ( 2 Т xi ) + ( 2 Т yi ) + ( 2 Т zi ) . (15)

V i = 1                   i = 1                   i = 1

Максимальное поле рассеивания замыкающего звена должно быть равно или меньше допустимого отклонения, тогда nnn

( 2 т x-v + ( 2 Т ¹ + ( 2 Т zi ) ² . (16) i = 1                   i = 1                   i = 1

Согласно формулы (16) при Лmin= 0 направление замыкающего звена совпадает с диагональю суммарного параллелепипеда, который является областью рассеивания конца суммарного вектора замыкающего звена и максимально возможной величиной при различных сочетаниях допусков и размеров координат, что обеспечивает сходимость итерационных процессов достижения заданной точности построения размерных цепей.

Для определения граничных точек областей рассеивания составляющих векторов рассмотрим методику расчета области рассеивания для плоской размерной цепи. Предельные значения параметров можно найти по заданным отклонениям первых двух составляющих векторов, например, например, для параметра X — по формулам: Xmin = АХ + ЕLХ, Xmax = АХ + ЕSХ, где А — номинальное значение параметра х; Е Х — нижнее отклонение параметра х; ESX — верхнее отклонение параметра х. Для облегчения суммирования и возможности автоматизации расчетных работ нумерация вершины многоугольников, аппроксимирующих область, ведется против часовой стрелки (рис. 3)

В табл. 1 приведены сочетания параметров, определяющих область рассеивания составляющих векторов ai в первой четверти координат в зависимости от способа задания размерных цепей. Формулы для определения граничных точек векторов в прямоугольных и полярных координатах приведены в табл.. 2

Вариации сочетаний предельных значений параметров позволяют формировать массивы областей рассеивания основных граничных точек областей. Для областей, заданных способами № 1, 3, 5, этих точек достаточно, чтобы оценить предельную область рассеивания составляющего вектора плоской размерной цепи, так как характер фигуры этих областей выпуклый. Для способов № 2, 4, 6 задания основных граничных точек области недостаточно, так как четыре граничные точки не дают полного представления о фигуре области. Например, для способа № 6 фактическая фигура области есть часть кольца.

Четыре граничные точки, соединяемые прямыми линиями, создают представление о фигуре в виде трапеции. Для способов № 2, 4, 6 на радиусных участках между основными точками производится аппроксимация участков окружности в зависимости от необходимой (заданной) точности расчета. Шаг аппроксимации А(р) определяется по формуле

З

Дф = 2arccosl 1 —— к А где А - радиус дуги окружности; ЗП - стрелка прогиба.

Точность расчета определяется коэффициентом аппроксимации - отношением З П к допуску Т А на радиус окружности А . Мера точности расчета

С = -ЗП- а ТА, где Т А = А max – А min. Минимальный угол аппроксимации Дф = у можно найти по формуле у = 2arccos

г

1 - C a 1 -к

I A l min

A

max /

Для седьмого способа задания области рассеивания составляющего вектора размерной цепи координаты xi

= A _x +

TA

^cos ( ф + у ) ;

x _i

= A y

TA

+ — 2"-^LSin фф + у ) ,

где Аx, Аy— координаты конца вектора-номинала; ф — угол между вектором-номиналом и осью Ох; у — минимальный угол аппроксимации.

За первую граничную точку области рассеивания принимается точка с минимальными значениями модуля вектора, т. е.

I A l .in =1 A l + EIVA .

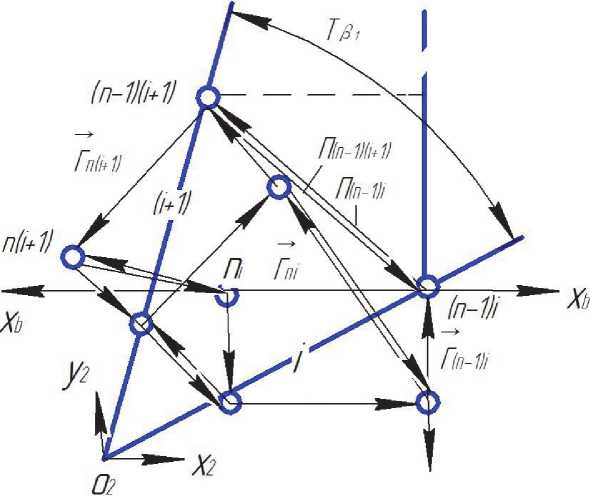
Рис. 3. Схема формирования области рассеивания составляющего звена для определения граничных точек областей рассеивания составляющих векторов

Таблица 1. Сочетания параметров

Номер способа	Параметры				Г	раничные точки области с номерами
	ах	а у	и	ф	1	2	3	4
1	*	*			x min , y min	x max, y min	x max, y max	x min , y max
2	*		*		1 Д 1 x min , l^lmtn	x max ,     min	1 1 x max ,     1 тОХ	1 1 x min ,
3	*			*	x min ,    min	x max,   min	x max,   max	x min ,    max
4		*	*		1 Д 1 y min ,      min 1	y max ,     min 1	y max ,    1 max	y min,              |
5		*		*	y min, '■?■■ min	y max, '■?■■ min	y max ,    max	y min , '■У max
6			*	*	^ 1 Фmin	^ 1 max >Ф min	1-^ 1 max >Ф max	1 1     ' Ф max

Таблица 2. Определение граничных точек векторов в прямоугольных и полярных координатах

Номер способа	Известные параметры вектора	Параметры вектора в пря моуг оль ных координатах		Параметры вектора в полярных координатах
					Vj
1			Yi	j'xr - УГ	arctg (yi/xi)
2	х„К|		I A2 —	-A	arccos (xi/Ai)
3	xi^L	xi	Xi/tSVi	x, /coso	Vj
4	У„К1	J At - Yj	Yi	A	arcsin (yi/Ai)
5	yLJ qr	Yi/^	Yi	Yi/sinTj	^i
6	K<9i	cosq).	sirup	A:	Vj

Получение окончательных размеров сборочной единицы есть процесс переноса размеров и форм, заданных графически в конструкторских чертежах путем воспроизведения их в размерах и формах деталей и изделий с помощью технологической оснас- тки, оборудования и измерительных средств.

Окончательные размеры сборочных единиц самолетных конструкций зависят от следующих видов погрешностей, накапливаемых в процессе производства.