Методика применения роевого интеллекта при управлении формированием портфеля ценных бумаг

Процесс управления портфелем ценных бумаг является высокоприоритетным в инвестиционной деятельности, так как фондовые рынки играют ключевую роль в финансовой системе государства и формируют среду для создания капитала, определяющего уровень национального богатства и благополучия общества. Задача формирования оптимального портфеля ценных бумаг традиционно опирается на два критерия – доходность и риск, и поэтому решение реализуется в два этапа согласно методике, описанной в [2]. На первом этапе необходимо выделить портфели с минимальным значением риска, на втором – из выбранных вариантов найти портфель с максимальной доходностью. Особенностью решения задачи портфельной оптимизации является применение семейства индексно-энтропийных мер риска, предложенных в [9]. Для снижения риска необходимо применять диверсификацию портфеля, что позволит устранить разброс в уровнях доходности различных финансовых активов. При диверсификации количество активов в портфеле возрастает, и применение метода прямого перебора для расчета целевых функций риска и доходности становится проблематичным из-за экспоненциального роста потенциальных

Методика применения роевого интеллекта при управлении формированием портфеля ...

Бронштейн Ефим Михайлович доктор физико-математических наук, профессор, профессор кафедры вычислительной математики и кибернетики Уфимского государственного авиационного технического университета, город Уфа. Сфера научных интересов: выпуклый анализ, финансовая математика, оптимизация, теория риска, задачи маршрутизации. Автор 140 опубликованных научных работ.

портфелей, которые образуют область поиска, то есть возникает необходимость применения численных методов для поиска эффективного портфеля. В настоящее время находят широкое применение алгоритмы, основанные на природных системах, например, генетические, эволюционные, поведенческие, алгоритмы роевого интеллекта и др. Рассмотрим некоторые роевые алгоритмы с целью выбора метода, который адекватно учитывал бы особенности решаемой задачи.

Методы роевого интеллекта

Методы роевого интеллекта моделируют коллективное поведение децентрализованных самоорганизующихся живых систем [5], таких как стаи птиц, косяка рыб, колонии муравьев, роя пчел и др. Муравьиный алгоритм основан на поведении муравьиной колонии в части поиска пути до пищи и описан в [6] Марко Дориго. Муравьи прокладывают тропы от найденного источника пропитания до места колонии, оставляя феромоновый след, на который ориентируются другие муравьи. Чем длиннее путь, тем меньшее количество проходов муравьи успеют по нему сделать, и концентрация феромона на такой тропе будет меньше, нежели на короткой траектории, где высокая плотность феромонов будет привлекать еще больше агентов. Концентрация феромонов на длинных тропах будет стремиться к нулю, а все муравьи в итоге придут по кратчайшему пути.

Пчелиный алгоритм предложен Д. Карабога в 2005 г. [8] и имитирует поведение пчел при поиске цветочного нектара. Пчелы-«разведчики» (5…10 % от всей колонии) отправляются в случайном направлении для исследования мест на предмет качества и количества находящейся там медовой пыльцы. По возвращении они посредством «танца» передают информацию о направлении и расстоянии до места пчелам-«работникам», которые принимают решение следовать за тем или иным «разведчиком». Разведанные точки сбора меда делятся на «лучшие» и «перспективные» на основе критерия оптимальности. Пчелы-«работники» производят случайный поиск в окрестности выбранной точки («лучшей» или «перспективной») и несут нектар в улей, что соответствует обмену информацией о значении целевой функции между всех пчел в рое. Данный метаэвристи-ческий алгоритм использует концепцию локального поиска, для которого необходимо

Информационные технологии и оптимизация управления наличие топологического расстояния на области решений для корректного определения подобластей.

Согласно алгоритму светлячков, предложенному Янгом [13], поисковые агенты характеризуются яркостью, которая в природе служит средством коммуникации между насекомыми для сообщения об опасности, для привлечения особей противоположного пола и др. Движение менее ярких светлячков в сторону более ярких (привлекательных) является основой метода. Яркость светлячка, воспринимаемая другой особью, снижается с увеличением расстояния между ними, и тогда в случае, если рядом нет привлекательного агента, светлячок движется случайным образом. Так как векторной координатой агента являются значения долей акций, входящих в портфель, то расстояние между портфелями определяется разницей между процентным соотношением эмитентов, но данная характеристика не определяет «привлекательность» ПЦБ. Поэтому формула привлекательности e i,j = в ₀ ■ exp( -Y ■ r i²j ), где e i,j — привлекательность i -го светлячка для j -го свтлячка, Г 2 j - расстояние от i -го до j -го светлячка, не отражает специфику поставленной задачи.

Алгоритм роя частиц описывает модель поведения птиц в стае. В каждый момент времени частица характеризуется положением и вектором скорости перемещения, которые обновляются согласно формулам, описанным в [11]. Для каждого положения частицы высчитывается целевая функция, значение которой на первой итерации фиксируется как лучшее персональное решение, а на последующих итерациях оно может быть обновлено. На каждой итерации среди всех лучших персональных решений выбирается оптимальное, тогда глобальное решение всего роя может быть обновлено. Таким образом, частицы движутся к наилучшей точке роя, учитывая свой индивидуальный оптимум.

Исходя из особенностей каждого метода, описанные выше алгоритмы на практике имеют свою область применения: муравьиный алгоритм используется для решения задачи коммивояжера, раскраски графа, оптимизации сетевых графиков, задачи анализа образовательных данных [3]; пчелиный алгоритм – для оптимизации управления, классификаторов, сложных транспортных задач [10]; алгоритм светлячков – для оптимизации проектирования технического объекта [4], для задач компьютерного зрения [7]; метод роя частиц – для решения задач машинного обучения, оптимизации функций многих параметров и др.

В работе [1] проведен сравнительный анализ роевых алгоритмов с точки зрения скорости сходимости – минимального числа вычислений целевой функции, требуемого для получения решения с заданной точностью, и надежности – доли успешных прогонов, когда ошибка меньше заданной заранее. Результаты показали, что, опираясь на эти критерии, нельзя с уверенностью утверждать о преимуществе одного из методов, так как лучшие результаты достигались для разных функций, а также для разного количества переменных (в случае одной и той же функции) разными алгоритмами.

Несмотря на то, что все упомянутые алгоритмы роевого интеллекта основаны на генерации многоагентной системы, специфика решаемой задачи накладывает ограничения на применение того или иного метода. Например, для решения поставленной оптимизационной задачи пчелиным алгоритмом целесообразно формировать область окрестности точки исходя из критерия меры риска, чтобы портфели, принадлежащие области, были соизмеримы по степени риска, а лучшее решение подобласти выбирать на основании максимальной доходности. Но алгоритм колонии пчел не учитывает данное требование двух-этапности в решении задачи поиска оптимального портфеля ценных бумаг, и возникают трудности при использовании пчелиного алгоритм в «чистом» виде.

Методика применения роевого интеллекта при управлении формированием портфеля ...

Результатом муравьиного алгоритма является оптимальный путь (граф) с несколькими узлами, которым при решении поставленной задачи соответвовали бы различные по структуре портфели. На выходе формировался бы пул альтренатив, что не позволило бы предложить инвестору оптимальный вариант и реализовать поддержку при принятии решения без применения дополнительных инструментов.

Кроме того, применение муравьиного алгоритма и метода свелячка не позволяет одновременно использовать семейство мер риска, а отдельный запуск вычислительной процедуры для каждой модели оценки риска увеличивает количество расчетов целевой функции и снижает преимущество использования численного метода оптимизации. Метод роя частиц (МРЧ) позволяет использовать многороевую версию алгоритма, где каждому рою соответвовует определенная модель оценки риска, и реализует возможность одновременного использования семейства мер. Таким образом, анализ роевых алгоритмов показал, что для решения поставленной двухэтапной оптимизационной задачи наибольшее преимущество имеет метод роя частиц согласно критериям и области применения, соответствия особенностей алгоритма специфике рассматриваемой задачи.

Параметры алгоритма роя частиц для поиска оптимального портфеля

Пространством поиска является n - мерный куб U = [ 0,1 ] n , а положение i -й частицы роя x j_t соответствует определенной структуре портфеля ценных бумаг в момент времени t . Структура задана вектором X = ( x 1 , x ₂,..., x n ) , здесь x j - доля j -ой акции в портфеле

n

( j = 1, n ) , т.е. X j >  0, 2 X j = 1, где n - количество акций. На положение частицы и ее ско-

V '                        j=i                          n                  n рость накладываются ограничения: ^x j t = 1,2V, t = 0, ах’te [0,1). Положение каж- j=1

j = 1

дой из частиц определяется как корректировка координаты частицы в предыдущий мо- мент времени на ее текущую скорость: xi, t+1 = vi,t+1 + xi,t. Скорость каждой частицы в рое vi,t+1 = c0 ■ vi,t + c 1 ■ Rand( ) ■ (Pitt - xi,t ) + c2 ■ Rand( )•(gt - xi,t ), (1)

где g _t - координаты наилучшей точки всего роя (портфель с рекордной доходностью) в момент времени t ; p i , _t - координаты наилучшей точки, найденной агентом - частицей (портфель, соответствующий минимальной мере риска), к ( t + 1 ) - му моменту времени; c ₀ , c 1 , с ₂ -весовые коэффициенты, которые отражают силу влияния предыдущего положения, персонального лучшего значения частицы и глобального лучшего найденного решения.

Для нахождения лучшего персонального решения частицы в конкретном рое ( p l , i , _t ) используется значение меры риска F l ( x i , _t ) ^ min , где l - номер роя. В качестве семейства мер используются комбинированные индексно - энтропийные меры риска, описанные в [9]. Поиск наилучшего решения g _t осуществляется среди всех персональных лучших значений частиц p l , i , _t всех рассматриваемых роев, что позволит обеспечить взаимодействие частиц между роями. Критерием для обновления g _t является функция доходности портфеля, которую необходимо максимизировать. Таким образом, в отличие от канонического МРЧ при нахождении персональных и глобальных оптимумов используется минимаксный подход.

На полученный оптимальный результат влияет размерность зоны поиска или количество исследуемых портфелей, которое зависит от произведения количества частиц ( S ) в рое на количество итераций ( k ). Баланс между количеством генерируемых частиц и коли-

Информационные технологии и оптимизация управления чеством итераций позволит настроить оптимальную скорость работы алгоритма с точки зрения затраченного на поиск решения времени и эффективности найденного портфеля.

Вычислительный эксперимент

Траектория движения агента является определяющим фактором для достижения оптимума, а новое положение частицы на каждой итерации зависит от значения вектора скорости, поэтому настройка параметров функции (1) необходима для получения эффективных решений. Для калибровки инерционного ( c ₀ ), когнитивного ( c ₁ ) и социального ( c ₂ ) коэффициентов был проведен вычислительный эксперимент по следующей сетке: c ₀ варьировался от 0,529 до 1,529, а с 1 и c 2 изменялись от 1,09445 до 1,99445 с шагом 0,1. Расчеты показали, что алгоритм достигает рекордных значений доходности портфеля при следующих сочетаниях параметров: (0,829; 1,99; 1,99), (0,929; 1,49; 1,49) и (0,129; 1,69; 1,69).

Для анализа качества портфелей, попавших в зону поиска разными путями, проведен вычислительный эксперимент, в котором исследованы 400 портфелей, сформированных согласно трем стратегиям: S ₁ = 100, k ₁ = 4; S ₂ = 4, k ₂ = 100; S ₃ = 20, k ₃ = 20. Портфели, сформированные каждым агентом в каждой точке пути, были оценены с помощью индекса Херфиндаля – Хиршмана, который показывает качество портфеля с точки зрения диверсифици-руемости [12]. H - индекс варьируется в диапазоне т 0 до 1, чем он меньше, тем более диверсифицируемый портфель, тем он менее рискованный. Кривые на рисунке 1 показывают, что наибольшая вероятность сгенерировать портфели с наименьшим H - индексом у стратегии 2.

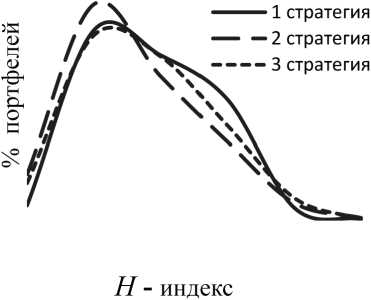
Рис. 1. Сравнение стратегий согласно динамике H -индекса и долям диверсифицируемых и не диверсифицируемых портфелей

В данном эксперименте портфель состоял из 4 акций, поэтому хорошо диверсифицируемые портфели соответствуют индексу Херфиндаля – Хиршмана, принадлежащему интервалу [0,25; 0,45]. С точки зрения количества хорошо диверсифицируемых, а значит, менее рискованных портфелей ранжированный список следующий: стратегия 2, стратегия 3, стратегия 1.

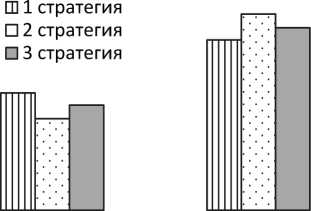
Далее был рассчитан процент портфелей, которым соответствует большой риск, в которых доля одного эмитента превысила 80–0,5, 1,5 и 2 % соответственно стратегиям. Область поиска тем лучше, чем меньше таких портфелей в ней. Стратегия 1 показывает сравнительно лучший результат, но разница с конкурирующими стратегиями несущественная, так как не превышает 1,5 %.

Принимая во внимание второй критерий оптимизационной задачи, стратегии исследовались с точки зрения доходности оптимальных портфелей (рис. 2). Была высчитана доля портфелей с максимальной доходностью (17–18 %): для стратегии 1 – 11,5 %, для

Методика применения роевого интеллекта при управлении формированием портфеля ...

стратегий 2 и 3 – 10,25 %. Все стратегии относительно в равной степени позволяют сгенерировать портфели с максимальной доходностью. Согласно диаграмме рассеяния (рис. 2) портфели с доходностью более 11 % составляют для стратегии 1 – 98,25 %, для стратегии 2 – 84,25 %, для стратегии 3 – 91 % от всего количества.

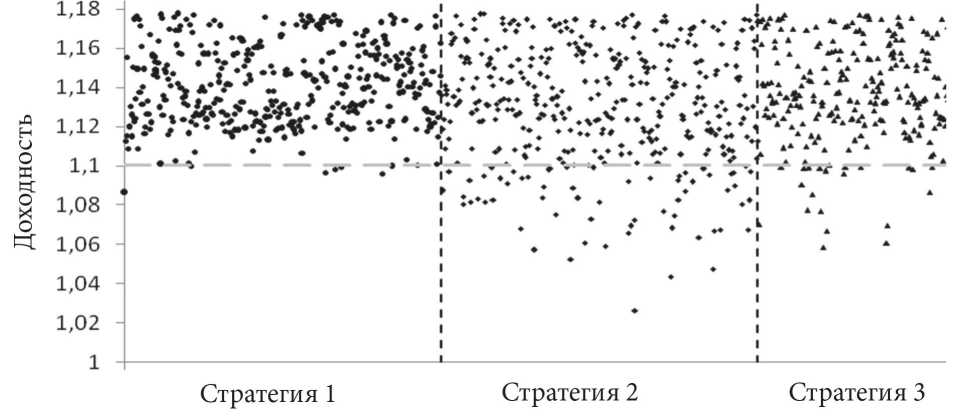
Рис. 2. Сравнение стратегий согласно доходности портфелей

Скорость сходимости алгоритма оценивалась согласно номеру итерации, на которой алгоритму удалось сформировать оптимальный портфель с максимальной доходностью. Результаты расчетов показали, что 75 % оптимальных решений были достигнуты на итерациях в диапазоне от 2 до 17, что позволяет сделать вывод о том, что 1-я и 3-я стратегии более предпочтительней, чем 2-я стратегия.

Результаты вычислительного эксперимента не позволяют сделать выбор в пользу одной стратегии, поэтому для формирования области поиска предлагается использовать стратегию, которая по своим характеристикам является гибридом 1-й и 3-й стратегий. Параметры S и k динамически изменяются в зависимости от количества акций ( n ) в портфеле, чтобы доля исследуемых портфелей в общей массе возможных портфелей была пропорциональна. Предлагаемая концепция позволит обеспечить такой размер области поиска, который будет достаточен для нахождения оптимального портфеля. Итак, результат настройки диапазонов параметров МРЧ приведен в таблице 1.

Таблица 1

Варьируемые параметры МРЧ

Параметр	Нижняя граница	Верхняя граница	Шаг изменения
Коэффициент инерции, c 0	0,829	1,129	0,1
Когнитивный коэффициент, c 1	1,49	1,99	0,1
Социальный коэффициент, c 2	1,49	1,99	0,1
Количество частиц роя, S	15 n		–
Количество итераций, k	2S/5		–

Информационные технологии и оптимизация управления

Выводы

Сравнительный анализ роевых алгоритмов показал, что для решения двухкритериальной задачи поиска оптимальной структуры инвестиционного портфеля предпочтительней метод, имитирующий поведение стаи птиц: один критерий используется для нахождения персонального лучшего решения частицы, второй – для поиска глобального решения роя. Многороевой алгоритм дает возможность одновременно использовать несколько комбинированных индексно-энтропийных мер риска, что в перспективе при появлении новых альтернативных инструментов оценки риска позволяет легко реализовать масштабирование разработанного алгоритма путем добавления роя.

Параметры области поиска решений настроены с опорой на оба критерия оптимальности: риск учтен посредством расчета степени диверсифицируемости портфеля через H -индекс, доля оптимальных портфелей с рекордной доходностью являлась метрикой для настройки параметров S и к . В результате исследования найдены коэффициенты ( c 0 , с 1 , c 2 ) математической модели метода роя частиц, которые рекомендовано использовать инвестору для решения задач портфельной оптимизации.