Методика применения средств компьютерной графики для исследования течения нестационарных процессов в современном материаловедении

Введение. Компьютерная графика все более широко внедряется в технику: разработка чертежей с помощью различных графических редакторов, твердотельное моделирование, системы САПР и т.д. Однако это применение не исчерпывает все ее возможности, поскольку некоторые элементы компьютерной графики могут найти реальное применение при исследовании течения нестационарных процессов и тем самым позволят получить более широкий спектр экспериментальных данных.

Ранее [ 1, 2 ] была показана возможность использования компьютерной графики при визуализации процессов в учебных и научных целях. Кроме этого, существует еще одна проблема, которая может быть успешно решена с помощью средств компьютерной графики.

В процессе проведения различного рода исследований часто возникает потребность обработки экспериментальных данных в целях получения каких-либо дополнительных характеристик. Для этого могут быть использованы математические методы, которые применяются в специальных программах, предназначенных для обработки экспериментальных данных, таких, как Math-CAD, MatLab, Excel и др. Однако применение таких пакетов требует серьезных познаний в математике, а также подбора определенных математических функций и выбора аргументов. При этом универсальные математические пакеты не ориентированы на конкретный тип и структуру экспериментальных данных, и такие программы предназначены в основном только для обработки результатов эксперимента. Вместе с тем область проводимых экспериментальных исследований настолько широка, что ни один из существующих универсальных пакетов обработки данных эксперимента не может обеспечить полное выполнение задачи исследователя, тем более при обработке сигнала, поступающего с какого-либо датчика, в режиме реального времени.

В последнее время компьютеры успешно применяются в качестве измерительных приборов, и это находит все большее распространение в научно-исследовательской практике. При этом возникает возможность не только регистрировать электрический сигнал, поступающий на вход компьютера, но и проводить его обработку с целью получить какие-либо новые характеристики. Оборудование и программное обеспечение. Рассмотрена возможность использования средств компьютерной графики при обработке экспериментальных данных, поступающих в виде электрического сигнала в режиме реального времени. При этом электрический сигнал подавался на вход ЭВМ через аналогово-цифровой преобразователь (АЦП), собранный по схеме и работающий по управляющей им программе [ 3 ] . Слабым электрическим сигналам требовалось усиление, для чего применялся прецизионный усилитель, собранный по определенной схеме [ 4 ] .

Постановка задачи. Известно [5], что протекание любого физического процесса, например нагрев или охлаждение металла, можно представить в виде графика «пройденного пути». Дифференцирование элементарного участка этого пути дает значение «скорости», а дифференцирование элементарного участка графика скорости дает, соответственно, величину «ускорения». Обработку подобных графиков «пройденного пути» можно выполнить с помощью графического дифференцирования, проводимого ЭВМ. В данном случае была использована программа на TurboBasic [3], которая позволяла выводить на экран дисплея ЭВМ график течения процесса. После ее переработки с помощью метода графического дифференцирования появилась возможность от- слеживать не только график самого нестационарного процесса, но и обрабатывать полученные в реальном времени экспериментальные данные и получать одновременно на экране ЭВМ сразу несколько характеристик, т.е. график самого нестационарного процесса (график «пройденного пути»), а также график «скорости», а при необходимости и график «ускорения», что позволяет визуально наблюдать за изменением изучаемого процесса, значительно сокращая время на обработку экспериментальных данных и получая более достоверные по точности результаты.

'Программа на языке ТВ с выводом на экран дисплея графиков изменения пути, 'скорости, ускорения и формирования обменного DXF.

• 1    CLS: Screen 9

• 2    Window(0,297)-(420,0)

• 3    Print "Записывать данные чертежа в DXF (Y/N)"

• 4    j$=inkey$: if j$="" then 4

if j$="n" goto 5

if j$="y" goto 6

• 5    regim=1: goto 13

• 6    regim=2: goto 7

'Открытие DXF чертежа

• 7    line input "Задайте имя DXF чертежа: ";PL$

• 8    open "o",1,PL$+".DXF"

• 9    print #1,0

• 10    print #1,"SECTION"

• 11    print #1,2

• 12 print #1,"ENTITIES"

'Ввод данных

13 XX=0:YY=0:XXv=0:YYv=0:XXa=0:YYa=0:XX1=0:YY1=0:XXv1=0:YYv1=0:

XX2=0:YY2=0:XXv2=0:YYv2=0:x=0:y=0:n=400:tk=29:tz=0.03:j=tk/tz:h=n/j:Tpr=0

Ms=55: Mv=10 :Mv1=1: Mv2=1: Ma=10: sd=10:

'Выполнение чертежа и запись в DXF

14 CLS: Mtimer: View (1,300)-(460,330),0,1: View (470,300)-(590,330),0,4:

View (600,300)-(638,330),0,5: View (1,1)-(638,290),0,10:

Line (XX,YY)-(XX,YY+280),4: if regim=1 goto 15

XS=XX: YS=YY: XF=XX: YF=YY+280: gosub 50

15 Line (XX,YY)-(XX+630,YY),4: if regim=1 goto 16

XS=XX: YS=YY: XF=XX+630: YF=YY: gosub 50

16 'драйвер TLC-549

OUT B+4,1: for T=0 to 100: next T

OUT B+3,64: for T=0 to 500: next T goto 150

100 OUT B+4,0: D=0: for F=0 to N-1

OUT B+4,2: E=INP(B+6) AND 16: OUT B+4,0

if E=16 then D=D+2^(N-1-F)

next F

D=5*D/(2^N-1): OUT B+4,1: Return

• 150:    'Вольтметр

160 Gosub 100

D=INT(100*D)/100: y=D: if x=0 then 18 else 19

• 18    YY=y: YYv=y: YYa=y:

• 19    Gosub 200

25 if x=n goto 30

if x>640 goto 30

Locate 23,2,0: Print "Tпр="(Tpr);"c.   " :Tpr=Tpr+tz if Tpr>tk goto 30

x=x+h: delay tz:

'Прерывание работы программы клавишей F12

ON KEY (31) gosub 999

KEY (31) ON goto 160

30 T1=Mtimer: T2=T1/1000000: Locate 23,2,0: Print "T="(T2);"c.   ":

if regim=1 goto 40

'Закрытие DXF

• 34    print #1,0

• 35    print #1,"ENDSEC"

• 36    print #1,0

• 37    print #1,"EOF"

• 38 close 1

39 Locate 23,60,0: Print "DXF= ";PL$

40 Locate 23,77,0: Print "END": beep

41 End

50 'Подпрограмма записи отрезка графика print #1,0: print #1,"LINE": print #1,8: print #1,"0": print #1,10

print #1,XS: print #1,20: print #1,YS: print #1,11: print #1,XF: print #1,21

print #1,YF: return

200 'Подпрограмма скорости в координатах X=V,Y=y y=y*Ms: Line (XX,YY)-(x,y),15 : if regim=1 goto 202

XS=XX: YS=YY: XF=x: YF=y: gosub 50

202 'скорость if x=0 goto 206

Vo=Vc: Vc=((sqr(((YYv-y)^2)+(h^2)))/h): Sk1=Vc*Mv

Line (XXv+sd,YYv)-(Sk1,y),14: if regim=1 goto 204

XS=XXv: YS=YYv: XF=Sk1: YF=y: gosub 50

204 XX=x: YY=y: XXv=Sk1: YYv=y

'ускорение if Vo=0 goto 206

Ay=((Vc-Vo)/h)*Ma: Line (XXa+sd,YYa)-(Ay+sd,y),13: if regim=1 goto 206

XS=XXa+sd: YS=YYa: XF=Ay+sd: YF=y: gosub 50

206 XXa=Ay: YYa=y: Return

999 beep: beep

В данном случае график самого процесса (т.е. график «пройденного пути») строился на основании данных величины электрического сигнала, полученного, например, от термопары, усиленного и поступающего на вход ЭВМ через АЦП. Этот сигнал проходил обработку по разработанной программе и в общем случае имел вид, представленный на рис.1. То есть такой график формировался по точкам Т 1 , Т 2 , Т 3 и т.д. При этом элементарный участок графика «пройденного пути»

S = V( X 2 - X 1 ) 2 + ( Y 2 - Y 1 ) 2 ,                                    (1)

где X 1 , Y 1 и X 2 , Y 2 – координаты соответственно начальной и конечной точек Т 1 и Т 2 .

Для получения значений скорости на этом участке «пройденного пути» проводилась обработка по приведенной выше программе методом графического дифференцирования в результа- те чего скорость

V      X 2 — X , ) 2 + ( Y 2 — Y ) ’

⁽ X 2 ^- X 1 )

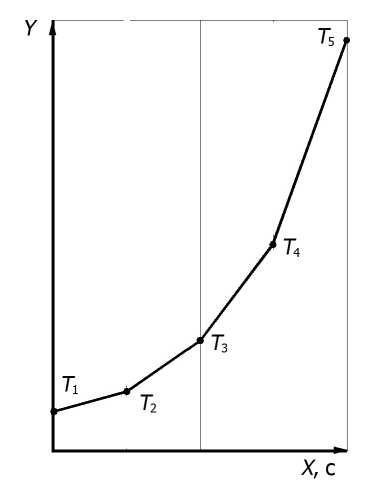
Рис. 1. График «пройденного пути» (фрагмент)

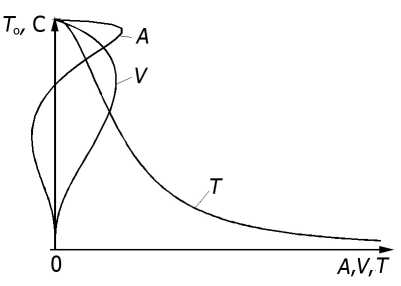
Рис.2. Термограмма охлаждения и ее производные – скорость и охлаждение:

Т – термограмма охлаждения образца;

V – график скорости охлаждения;

А – ускорение охлаждения

Кроме этого, в процессе эксперимента программа одновременно позволяла формировать обменный DXF-файл, который затем можно было перенести в какой-либо графический редактор, например AutoCAD, для дальнейшей обработки, сравнения, анализа, вывода графика на бумажный носитель и т.д. Такая методика и созданная для нее программа могут быть использованы, например, при проведении исследования охлаждающей способности закалочных сред, регистрации развития трещины методом электропотенциалов и других процессов.

Наглядным примером применения такой методики служат экспериментальные данные, полученные с термопары в процессе охлаждения (рис.2).

Разработанная методика была применена для исследования кинетики разрушения при развитии усталостной трещины в термически обработанных призматических образцах (рис.3).

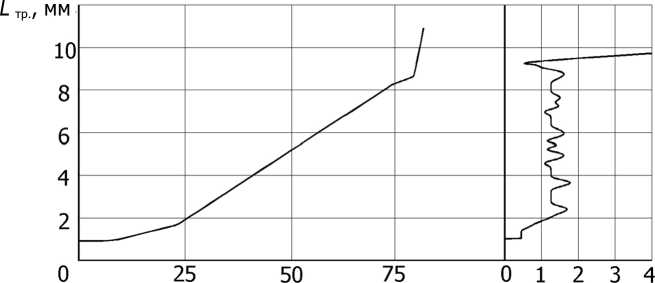
Л/хЮ4 циклов            УхЮ4, мм/цикл

Рис.3. Кинетика развития усталостной трещины и ее производная – скорость V

С другой стороны, можно проводить и интегрирование графика, что позволяет получать площадь фигуры, ограниченной кривой, характеризующей исследуемый процесс. Так, при интегрировании элементарного участка «пути» получается следующая площадь:

S = ( X 1 - X ) ) Y 1 ,                                        (3)

где X 0 , X 1 , Y 1 - координаты соответственно предыдущей и последующей точек измерения (рис.4).

Для реализации этого была разработана программа, позволяющая выполнять процесс графического интегрирования графика «пути».

200 'Подпрограмма построения графика

'разрушeния образца и определения работы

'зарождения Аz и развития Ар трещины

Line (XX,YY)-(x,y),15 : if regim=1 goto 202

XS=XX: YS=YY: XF=x: YF=y: gosub 50

202 Si=(y+YY)/2*(x-XX)

if y>YY then 204 else 206

206 Ap=Ap+Si

208 XX=x: YY=y:

204 Az=Az+Si

Return

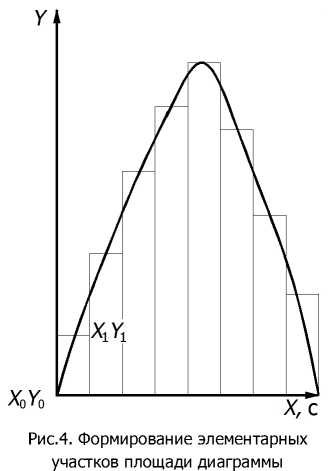
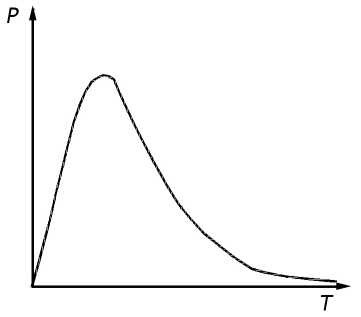
Рис.5. Диаграмма разрушения образца при испытаниях на динамический изгиб

В процессе работы этой программы каждый элементарный участок пути дает значения площади, которые затем суммируются и по окончании процесса получается результат – вся площадь под кривой, характеризующей процесс.

Данная методика обработки экспериментальных данных позволяет, например, автоматизировать процесс разделения на составляющие испытаний при ударном изгибе в целях получения значений работы зарождения и развития трещины. В этом случае в результате испытания на ударный изгиб призматического образца с надрезом на экране ЭВМ формировалось графическое изображение диаграммы разрушения в координатах «усилие – время» (рис.5). Методом графического интегрирования с помощью ЭВМ, работающей по разработанной программе, получали площади соответствующих участков диаграммы, которые использовались для дальнейших расчетов и определения составляющих ударной вязкости: работы зарождения и развития трещины по мето- дике, описанной в литературе [6]. В процессе работы такой программы проводилось суммирование площади до максимума функции графика разрушения образца, которая соответствовала работе зарождения трещины аз, а затем суммировалась следующая часть графика убывающей функции от максимума до конца процесса, которая соответствовала работе развития трещины ар. Сумма аз и ар соответствовала полной работе разрушения образца.

Заключение. Приведенная методика применения ЭВМ и средств машинной графики может быть использована при изучении практически любого нестационарного процесса как в учебном, так и в научно-исследовательском практикуме и будет отличаться лишь программой, обрабатывающей экспериментальные данные.