Методика приведения интегральных фотометрических измерений околоземных космических объектов к фотометрическому стандарту

ВЕСТНИК 2016

При проведении мониторинга околоземного космического пространства огромное значение имеют фотометрические измерения. Суть их заключается в получении временной зависимости дискретных замеров интенсивности отраженного от околоземного космического объекта (ОЗКО) солнечного излучения в течение определенного промежутка времени. Данную зависимость, полученную в течение одного сеанса наблюдений, будем называть фотометрической реализацией.

Фактически все современные оптикоэлектронные системы наблюдения ОЗКО оснащены ПЗС-камерами, которые обладают достаточно высокой чувствительностью и большой информативностью [1]. Применение ПЗС-камер позволяет на телескопах небольшого размера наблюдать малоразмерные элементы космического мусора. Также к достоинству ПЗС-камер следует отнести:

– возможность управления режимами функционирования;

– цифровое преобразование сигнала.

Измеряемой в ПЗС-кадре величиной эквивалентной интенсивности регистрируемого от ОЗКО сигнала является сумма дискретных значений градаций яркости выделенного изображения данного объекта:

I 03K0 = ^ B ( i ’ j ) ’ ⁽¹⁾ где B ( i, j ) - дискретное значение яркости ( i, j ) элемента ПЗС-матрицы. Суммирование реализуется в пределах выделенной площади S изображения КО. Для восьмибитового АЦП дискретность оцифровки будет составлять 0–255 градаций яркости.

Полученное значение I_OЗКО эквивалентно отклику измерительной системы, определяемой как свертка распределения энергии в спектре излучения ОЗКО с функцией инструментальной кривой реакции H ( Я ) , кривой реакции земной атмосферы P ( Я ) :

λ ₂

Такс = G = k f^ (^) H (^) P (^) d ^, (2) λ1

где k - коэффициент пропорциональности, а Я 1 и Я ₂ - границы области спектральной чувствительности измерительной системы «оптический объектив + ПЗС-камера».

Таким образом, фотометрическая реализация представляет собой массив значений { Iq_3K0 } , где t_k – момент времени дискретного измерения в k -ом ПЗС-кадре. Пример фотометрической реализации, полученной с помощью цифровой ПЗС-камеры, приведен на рис. 1.

ВЕСТНИК 2016

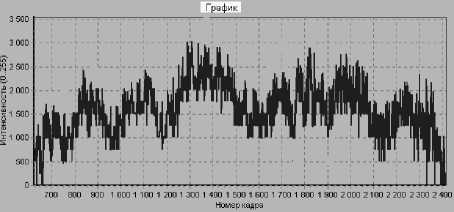
Рис. 1. Фотометрическая реализация ОЗКО 9005С (третья ступень ракеты-носителя), полученная на Звенигородской обсерватории ИНАСАН

Однако значение I_OЗКО индивидуально только для данной проводки и не может быть использовано при сравнительном анализе различных фотометрических реализаций, даже полученных на одном измерительном средстве в различных наблюдательных сеансах.

Поэтому возникает необходимость в определении стандартной фотометрической системы.

В практике обработки фотометрических измерений в качестве эталонной используется понятие «звездная величина». Это связано с тем, что в качестве эталонных источников излучения в фотометрических измерениях ОЗКО удобно использовать звёзды. При этом в рамках фундаментальных исследований создаются звездные каталоги на основе обработки данных большого количества обзорных наблюдений.

Для определения звездной величины ОЗКО используется следующее выражение:

т_0ЗК0 = — 2,5lg G + const,               (3)

где G – отклик регистрирующего прибора.

Константа в выражении (3) и определяет нам фотометрический стандарт. Это может быть одна звезда, значение которой известно с высокой точностью. Проведя текущую оценку G для данной звезды, можно определить значение данной константы.

К сожалению, спектры излучений звезд являются довольно сложными, что не позволяет использовать их в качестве идеальных излучателей. Данная особенность приводит к зависимости звездных величин в каталоге от параметров измерительной системы. При этом на точность фотометрических измерений влияет земная атмосфера (см. выражение (2)), параметры которой имеют значительную пространственновременную неоднородность [2]. Поэтому при реализации звездных каталогов используют алгоритмы редукции, позволяющие определить их внеатмосферную звездную величину.

Для повышения точности фотометрических измерений используют узкополосные фильтры. Однако при этом уменьшается чувствительность измерительной системы, что не позволяет проводить фотометрические измерения малоразмерных ОЗКО. Также узкополосность резко снижает информативность фотометрической реализации.

Поэтому фотометрические измерения околоземных космических объектов целесообразно проводить в интегральном диапазоне измерительной системы.

В данном случае используется следующая методика определения фотометрического стандарта.

В качестве исходных данных используется стандартный фотометрический звездный каталог. В настоящее время имеется более десяти достаточно полных фотометрических каталогов звезд. Однако большинство из них основано на обработке измерений, реализованных на фотопластинках или фотоэлектронных умножителях в соответствующих системах фильтров.

В настоящее время только один каталог Hipparcos содержит звездные величины порядка 118 000 звезд в фотометрической системе H_P , спектральный диапазон которой достаточно близко совпадает со спектральными диапазонами ПЗС-матриц (рис. 2)

На первом шаге измерительной системой осуществляются наблюдения определенного массива опорных звезд, содержащихся в каталоге Hipparcos. Для каждой звезды определяется звездная величина на основе принятия решения, что существуют эталонные звезды, для которых звездные величины в опорной и измерительной системах максимально совпадают.

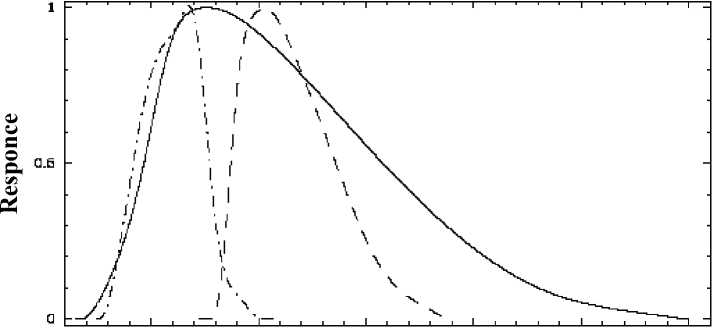
dOO          500          аоо          700          BQO          ООО

Wavelength (nm)

а) Фотометрические системы H_P ( сплошная линия ), V_T ( штриховая линия ) и B_T ( штрихпунктирная линия ), в которых приведены звездные величины в каталоге Hipparcos

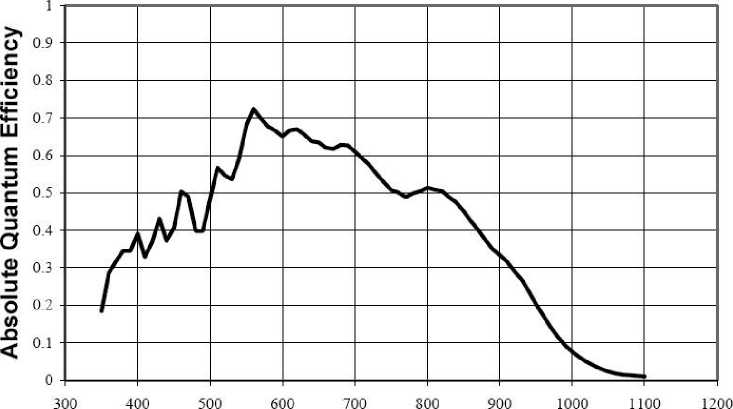
Wavelength (nm)

б) Спектральная чувствительность ПЗС-матрицы фирмы Кодак.

Рис. 2. Спектральные чувствительности измерительных систем

ВЕСТНИК 2016

Естественно, мы получаем массив разностей звездных величин { A m i } (). При этом необходимо измерения «вынести» за атмосферу, чтобы устранить влияние параметра P( λ ) в выражении (2). Решение данной задачи осуществляется, как правило, с помощью выражений, приведенных в работе [3].

Используя массив { A m i } с помощью метода наименьших квадратов (МНК), определяется редукционная зависимость:

МОС≈ F(ĬОЗКО), (4) где МОС звездные величины в опорной системе координат; ĬОЗКО – значение дискретной интенсивности с «выносом» за атмосферу.

Обычно это редукционный полином, содержащий определенные параметры.

Непосредственно перед проведением фотометрических измерений осуществляется уточнение выражения (4) на основе наблюдений опорных звезд.

В рассмотренной методике есть ряд проблемных аспектов.

Во-первых, для реализации МНК необходимо заранее задавать вид опорного полинома.

ВЕСТНИК 2016

Применяемые алгоритмы оценки степени полинома требуют дополнительного объема измерительных данных. При этом довольно трудно оценить взаимовлияние параметров, входящих в полином, друг на друга.

Во-вторых, разделение этапов оценки редукционного полинома (4) и алгоритма «выноса» за атмосферу приводит, с одной стороны, к упрощению процесса за счет декомпозиции выражения (2). Но в то же время исключаются из анализа аспекты влияния параметров атмосферы на изменение инструментальной кривой реакции H ( Я ) . Поэтому предлагается для приведения интегральных фотометрических измерений околоземных космических объектов к фотометрическому стандарту провести модернизацию рассмотренной выше методики.

Модернизация заключается в использовании для оценки комплексного редукционного полинома (4) метода группового учета аргументов, позволяющих найти регрессионную зависимость оптимальной сложности [4].

Метод наименьших квадратов, наиболее часто используемый при построении регрессионных зависимостей, не пригоден для нахождения модели оптимальной сложности из-за слабой помехоустойчивости внутренних критериев, к которым он относится. Согласно методу наименьших квадратов, чем сложнее модель, тем она точнее.

Задачу открытия единственной модели оптимальной сложности решают методы группового учета аргументов, основанные на помехоустойчивых «внешних» критериях.

Это не исключает эффективности метода наименьших квадратов при решении задачи приближенной аппроксимации функций внутри области интерполяции.

Понятие «внешнее дополнение» получило свое развитие в математической логике в связи с появлением теоремы неполноты Геделя. Согласно этой теореме, оказывается, что никакая система аксиом не может быть логически замкнутой: всегда можно найти такую теорему, для доказательства которой потребуется внешнее дополнение – расширение исходной системы аксиом [4]. Согласно теореме, критерии выбора моделей следует разделить на внутренние и внешние.

Критерий называется внутренним, если его определение основано на использовании той же информации, тех же данных, что и для получения самой модели.

Критерий называется внешним, если его определение основано на новой информации, «свежих» точках, не использованных при син-

тезе модели. Структура оптимальной сложности соответствует минимуму внешнего критерия.

Основное фундаментальное открытие методов группового учета аргументов состоит в том, что установлено существование минимума ряда эвристических критериев, обладающих свойствами внешнего дополнения, при постепенном усложнении математической модели. Именно существование такого минимума дает возможность передать вычислительной машине этап отыскания математической модели оптимальной сложности.

На начальном этапе задается исходный полином в следующем виде:

N

M = a 0 + y a^a n x n + yy a^1 ^a n 2 X 1 x n 2 +

0                                      (5)

+УУУа a a x x x n1 n 2 n3 n1 n 2 n3

•

Выражение (5) представляет собой запись полного полинома Колмогорова – Габора в виде многорядной системы полиномов. Каждая часть полинома рассматривается как самостоятельное частное уравнение регрессии, решающее задачу восстановления функции по ряду точек. Минимальное число измерений, необходимое для однозначного определения оценок коэффициентов полинома, на единицу больше числа членов частного полинома. Причем одни и те же измерения можно использовать для восстановления как всех частных полиномов, так и их полного

полинома.

Использование выражения (5) позволяет систематически уточнять редукционную зависимость за счет проведения новых измерений.

Коэффициенты в полиномах рассчитываются по методу наименьших квадратов, число N определяется исходя из минимума некоторого внешнего критерия селекции, а тип полинома выбирается на основе многорядной процедуры массовой селекции.

Для этого на каждом шаге используется критерий несмещенности, в котором все имеющиеся точки выборки V ( I ) ранжируются по величине дисперсии от среднего значения:

n

см

M

= Z j=1

N ₂

Z ( a ji ^- b ji )

2=1

NN

Z a ji + Z b 2

i = 1            i - 1

0,

где М – число различных коэффициентов, используемых в регрессионной модели; N – показатель степени регрессионной модели; a_ji – коэффициенты полиномов, полученные до перемены мест последовательностей; b_ji –

коэффициенты полиномов, полученные при перемене мест обучающей и проверочной последовательностей.

По этому критерию из ряда в ряд селекции пропускается T самых несмещенных полиномов. Селекция продолжается до тех пор, пока несмещенность не уменьшится.

Недостатком критерия несмещенности является недостаточно плавная характеристика в функции сложности модели [5]. Поэтому его следует применить совместно с критерием регулярности, который характеризуется величиной среднеквадратической ошибки, измеренной на новых точках отдельной проверочной последовательности данных:

N pr

К N (A- fA i,))

^A( 1 ) = - i =i—j-- > min,          (7)

N pr      2

Z( f) i=1

где A ( 1 ) - относительная ошибка; N ( I i ) - измеренное значение интенсивности в i -ой точке; f j ( I i ) - значение, полученное с помощью j -го опорного полинома в i -ой точке.

В данном случае используется следующее правило разбиения вектора исходных данных на обучающую и проверочные последовательности.

Последний элемент выборки входит в проверочную последовательность. Кроме того, сюда же входят элементы, отстающие от последнего на интервал времени упреждения, который задается не более 10% от всего объема выборки. Использование интервала упреждения вызвано сильной зашумленностью исходных данных и необходимостью осуществлять процесс аппроксимации путем нескольких последовательных итераций.

С помощью рассмотренной методики был создан опорный фотометрический звездный каталог для телескопа «Цейс-600» с ПЗС-камерой фирмы FLI в Звенигородской обсерватории ИНАСАН, который состоит из более 1000 опорных звезд. Были синтезированы редукционные полиномы связывающие звездные величины каталога Hipparcos с опорным каталогом и комплексный редукционный полином, позволяющий оценивать звездную величину ОЗКО относительно каталога Hipparcos непосредственно по результатам фотометрических измерений. Для этого необходимо провести дополнительные фотометрические измерения 10–12 опорных звезд с периодом не более 30 минут.

Применение разработанной методики приведения интегральных фотометрических измерений околоземных космических объектов к фотометрическому стандарту позволило обеспечить приведение интегральных фотометрических измерений к фотометрическому стандарту с СКО не более 0,03 звездной величины, что превосходит по точности классические методики более чем в три раза. При этом используется ограниченное количество дополнительных фотометрических измерений опорных звезд.