Методика проектирования репродукционных гибридных объективов-монохроматов с градиентными и дифракционными элементами



МЕТОДИКА ПРОЕКТИРОВАНИЯ РЕПРОДУКЦИОННЫХ ГИБРИДНЫХОБЪЕКТИВОВ-МОНОХРОМАТОВ С ГРАДИЕНТНЫМИ И ДИФРАКЦИОННЫМИ ЭЛЕМЕНТАМИ

В работе рассматривается машинно-графическое проектирование симметричного объектива, в котором в качестве силового компонента каждой из его половин используется одиночная градиентная линза. При этом предполагается, что распределение показателя преломления линзы описывается рядом

п(С) -^V' где п^ - коэффициенты разложения функции показателя преломления;

С - квадрат расстояния от оптической оси.

Используя выражения для монохроматических аберраций третьего порядка, полученные в [1], нетрудно показать, что у одиночной градиентной линзы могут быть одновременно устранены сферическая и все четные поле вые аберрации. Однако достичь при этом приемлемого уровня остаточных четных полевых аберраций высших порядков не удается.

Ситуация существенно изменяется, если отказаться от требования устранения составляющих сферической аберрации во всех порядках аберрационного разложения. В этом случае сферическую аберрацию симметричного объектива в целом можно устранить, поместив в плоскость апертурной диафрагмы дифракционную асферику, то есть дифракционный оптический элемент, имеющий нулевую оптическую силу и заданную сферическую аберрацию .

Задача устранения четных полевых аберраций одиночной градиентной линзы в приближении аберраций не выше пятого порядка сводится к обнулению двух аберрационных коэффициентов третьего порядка (астигматизма Вэ и кривизны Петцваля Ви) и пяти коэффи-центов пятого порядка (коэффициентов наклонной сферической аберрации МЯЮ' -^зооз^зю), астигматизма N2011 и кривизны ПОЛЯ      . Число конструктивных параметров при заданной оптической силе градиентной линзы, влияющих на перечисленные аберрации, равно числу независимых аберрационных коэффициентов. Следовательно, может быть поставлена задача одновременного устранения всех четных полевых аберраций в третьем и пятом порядках.

Эта задача решалась следующим образом. Задавшись некоторыми значениями коэффициентов разложения функции показателя преломления n , п и толщины линзы d, аналитически решалась система двух уравнений, обеспечивающих заданное фокусное расстояние f и выполнение условия Петцва-ля (В^=0). Из этой системы определялись кривизны поверхностей С =С3* Затем при заданных и вычисленных значениях параметров и некотором начальном положении апертурной диафрагмы t из условия устранения астигматизма третьего и пятого порядков определялись последовательно коэффи- циенты па и n3. Далее, используя уже найденные значения параметров, вычислялся коэффициент М2002 и организовывался итерационный процесс его обнуления путем изменения положения апертурной диафрагмы.

Аберрационные коэффициенты градиентной линзы вычислялись с использованием методики, изложенной в [2] и основанной на машинном расчете хода псевдолучей, траектория которых вычисляется в приближении аберраций

различных порядков.

Описанный выше цикл вычислений повторялся при заданных по и f' для ряда значений п1 и d с целью получения функциональной зависимости от этих параметров двух оставшихся не-обнуленными коэффициентов М2 и М2озо* Графики зависимостей этих коэффициентов от п5 для различных значений d при n0=l,7, f'=l представлены на рисунках 1а, 16. Из них видно, что, по крайней мере, отдельно каждый из аберрационных коэффициентов МД11О и М2О2О может быть обращен в нуль. Для того чтобы решить вопрос об их совместном обнулении, на основе графиков (рисунки 1а, 16) строилось семейство кривых М =f^i ) при изменении п и Фиксированных значениях d (рис. 2). Анализ этих кривых показывает, что при изменении толщины градиентной линзы d уменьшение по модулю одного из аберрационных коэффициентов сопровождается ростом другого. Изменить же характер взаимозависимости аберрационных коэффициентов путем перехода к существенно меньшим либо существенно большим толщинам не представляется возможным.

Это связано с тем, что при уменьшении толщины резко растут значения кривизн преломляющих поверхностей линзы и перепада ее показателя преломления. Сверху же толщина градиентной линзы ограничена возможностью обращения в нуль аберрационных коэффициентов Вй , М2002=М21о1. Это граничное значение толщины зависит от показателя преломления градиентной линзы на ее оси nQ (рис. 3). Таким образом, у одиночной градиентной линзы, свободной от четных полевых аберраций третьего порядка, возможно одновременное устранение трех из четырех различных четных полевых аберраций пятого порядка.

В этих условиях при компоновке симметричного объектива из двух градиентных линз и дифракционной асфе-

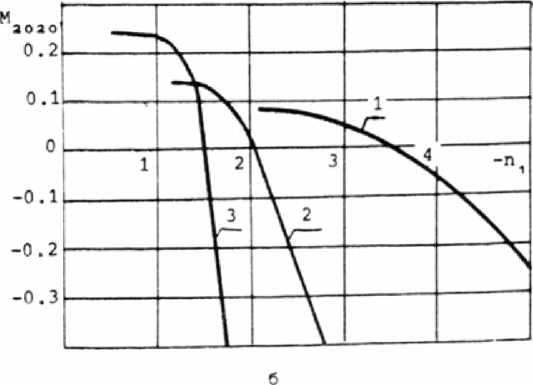
Рис. 1. Зависимости коэффициентов наклонной сферической аберрации Ма1 о (а) и кривизны поля пятого порядка М2020 (б) от коэффициента разложения показателя преломления п1 для ряда значений толщины градиентной линзы:

1 - d=0,2; 2 - d=0,4; 3 - d = 0,6

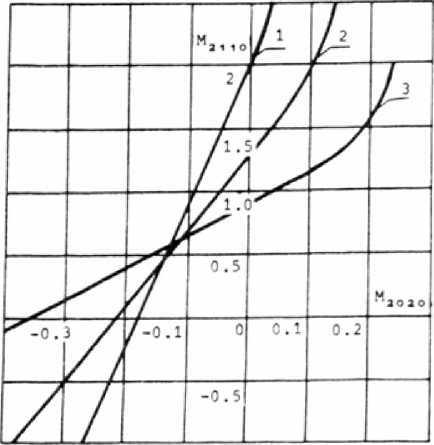
Рис. 2. Взаимные зависимости коэффициентом М211О и М2ОЗО для ряда значений d:

1 - d=0,2; 2 - d=0,4;

3 - d=0,6

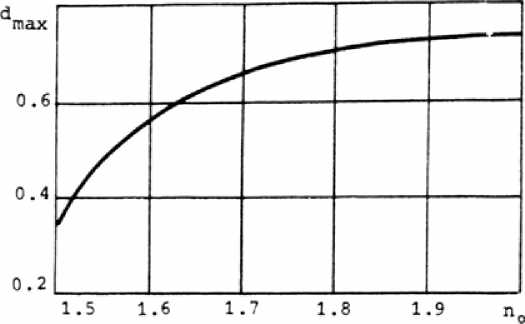
Рис. 3, Зависимость максимальной толщины градиентной линзы dmax (при которой возможно выполнение условия В»=Мзооз=М21О1=0) ОТ показателя преломления на ее оси п0

рики целесообразно устранить все аберрации, за исключением кривизны поля, что в приближении аберраций пятого порядка обеспечит формирова ние стигматического изображения на некоторой поверхности вращения. При проекции изображения на плоскость поле высококачественного изображения будет ограничено. Его можно расширить, отступив от выполнения условия Петцваля и оптимально сбалансировав кривизну поля третьего и пятого порядков .

В результате полученный гибридный объектив, состоящий из дифракционного и двух градиентных элементов, по степени компенсации монохроматических аберраций не уступает десятилинзовому объективу типа Фотон-3 [з] и занимает промежуточное положение между двух- и трех-линэовыми дифракционными объективами [4]. При этом в отличие от последних, благодаря низкой пространственной частоте единственного дифракционного элемента, гибридный объектив может иметь светопропуска-ние на уровне обычного объектива, а его хроматизм позволяет использовать излучение газоразрядных приборов, например, типа ртутной лампы.