Методика проектирования шнековых машин для экструзии пластичных сред

ЭКСТРУЗИЯ, ШНЕКОВЫЕ МАШИНЫ, ПЛАСТИЧНЫЕ СЖИМАЕМЫЕ СРЕДЫ, ФОРМУЮЩИЙ ИНСТРУМЕНТ, СИЛОВОЙ ШНЕК, МЕТОДИКА ПРОЕКТИРОВАНИЯ

Предметом исследования является методика расчета геометрических параметров и последовательность проектирования формующего инструмента и силового шнека экструдера для переработки пластичных сжимаемых сред.

Разработанная методика построена на основе теоретической модели, связывающей реологические свойства и триботехнические характеристики перерабатываемого материала с геометрией канала шнека и формующего инструмента экструдера. Даны примеры выполнения расчетов при проектировании экструдера, приведено краткое описание разработанного прикладного приложения для автоматизации проектирования.

Разработанная методика позволяет проектировать шнековые машины для экструзии пластичных сред с оптимальными геометрическими параметрами формующего инструмента и силового шнека, а ее реализация в виде прикладной САПР позволяет сократить время на подготовку трехмерных моделей и выпуск конструкторской документации. Результаты работы могут быть использованы при проектировании специализированного оборудования для шнековой экструзии изделий из композиционных материалов.

EXTRUSION, SCREW-TYPE MACHINES, PLASTICIZED COMPRESSIBLE MATERIALS, FORMING TOOL, EXTRUDER SCREW, DESIGN DEVELOPMENT TECHNIQUE

The subject of the study is calculating technique and design technique for geometric parameters of forming tool and screw of the extruder for plasticized compressible materials processing.

The developed technique is based on a theoretical model linking the rheological and tribotechnical properties of material with geometric parameters of screw channel and forming tool of extruder. Examples of performing this kind of calculations and brief description of developed software application are given.

The developed technique and software allows designing screw-type extruders for plasticized materials with optimal geometric parameters of forming tool and power screw, and allows reducing the time for 3D-modelling and drafting. The results of the work can be used in the design of specialized equipment for screw extrusion of composite materials.

45 )

Шнековые машины для переработки материалов методом экструзии применяются очень широко в различных отраслях: в химической, легкой промышленности [1], при переработке полимеров, в пищевой промышленности, в порошковой металлургии, и имеют общие конструктивные признаки. Однако оборудование, рассчитанное на формование материалов определенного состава, как правило, оказывается малоэффективным при переработке на нем других материалов. Это, в свою очередь, приводит к тому, что для переработки каждого вида материала требуется подбирать, часто экспериментальным путем, оптимальные геометрические характеристики формующих головок, силовых шнеков, а также определять оптимальные режимы переработки [2].

Исторически сложилось так, что теория шнековой экструзии развивалась по отдельности в разных отраслях народного хозяйства, в зависимости от свойств перерабатываемых материалов. В связи с широким применением шнековых экструдеров для производства полимерных изделий хорошо развита теория экструзии вязких жидкостей [3], позволяющая рассчитывать и проектировать формующие головки и шнеки для переработки термопластов. Однако невозможно прямое заимствование этой теории для процессов переработки других материалов, например, пластифицированных порошковых композиций, поскольку по реологическим и технологическим свойствам такие материалы сильно отличаются от расплавов полимеров. Существуют специализированные программные пакеты для компьютерного моделирования процесса экструзии (например, наиболее известны Qform Extrusion, Compuplast Virtual Extrusion Laboratory, Click2Extrude), выполняющие расчеты с применением метода конечных элементов (МКЭ). Область применения таких программных средств также, как правило, ограничивается экструзией изделий из полимеров и цветных металлов.

Современное промышленное производство требует как легко перенастраиваемого многофункционального оборудования для экструзии, так и универсальных методик его расчета и проектирования. В работе [4] приведены теоре- тические основы экструзии сжимаемых пластичных сред. Разработанная теоретическая модель учитывает реологические свойства и триботехнические характеристики перерабатываемого материала, определяемые с помощью специальных экспериментальных методик, и связывает их с оптимальной геометрией канала шнека и формующей головки экструдера.

Для практического применения теории необходимо разработать научно обоснованную технологию проектирования шнекового оборудования и реализовать ее в виде автоматизированной системы проектирования. В данной работе рассмотрена методика расчета конструктивных параметров и последовательность проектирования формующего инструмента и силового шнека экструдера для переработки пластичных сжимаемых сред.

На первом этапе проектирования должны быть определены геометрические параметры формующего инструмента (матрицы). Зона деформации материала формующим инструментом схематично показана на рисунке 1.

Формуемый материал (рисунок 1) выдавливается (слева направо по схеме) через зазор, образованный внутренней поверхностью матрицы 1 и наружной поверхностью дорна 2. Матрица имеет коническую (входную) часть длиной z₁ и цилиндрическую (калибрующую) часть длиной z₂ – z₁ . Радиусы входного и выходного сечений матрицы r₂ и r₁ , угол наклона образующей конуса α , радиус дорна r₀ . Предполагается, что дорн перемещается в процессе экструзии вместе с материалом.

На материал действует усилие выдавливания, вызывающее напряжения σ _z , которые однородно распределены в поперечных сечениях. На внутренней поверхности матрицы действуют нормальные напряжения σ и касательные напряжения τ . На поверхности дорна действуют нормальные напряжения σ _r , касательные напряжения отсутствуют. Направления главных нормальных напряжений совпадают с координатными направлениями.

В цилиндрической части матрицы материал находится в состоянии упругой разгрузки с элементами пластического течения, при этом справедливо соотношение

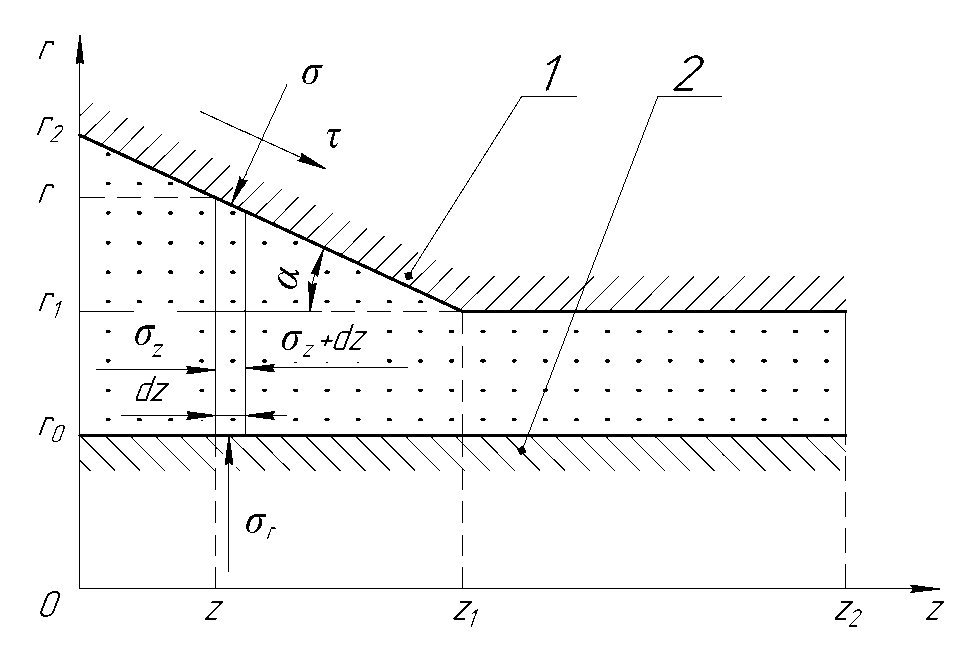
Рисунок 1 – Схема деформации материала в формующей головке экструдера

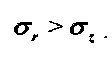
Условие пластичности для всей зоны формования имеет вид

Связь касательных и нормальных напряжений зададим линейным законом трения, поскольку в матрице находится уже спрессованный до компактного состояния материал:

,

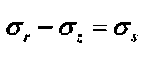
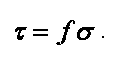
где σ_s – предел текучести материала при сжатии.

Уравнение равновесия сил, действующих на кольцевой элемент толщиной dz

f

»_t(r²- ^т0 >- (^ + ^ )K^r - - r/ ]+

Подставляя закон трения (5) и условие пластичности (2) в (4) и учитывая, что σ_r = (cos α – – τ sin α ) / cos α = σ( 1 – ftg α) , получим

+ (r - ,    (3)

или, после удаления бесконечно малых величин высших порядков

где

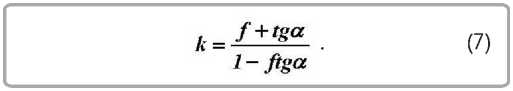
2     2

'о ~r

x 6a

) —- + 2r a.tga - 2r(atga + т) = 0 . (4)

’ 07.                               "

После разделения переменных и подстановки r = r ₂ – ztg α получается уравнение

(ICT. 2(гг - aga) = 2,2  .  .2 4 (8) (A - tga)cra + ka^ , r„ -(r-agay условии σz(z2) = 0 дает следующую зависимость для распределения напряжений на цилиндрическом участке матрицы:

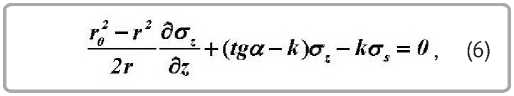
интегрирование которого дает

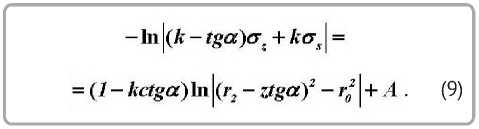
Постоянная интегрирования A определяется из граничного условия

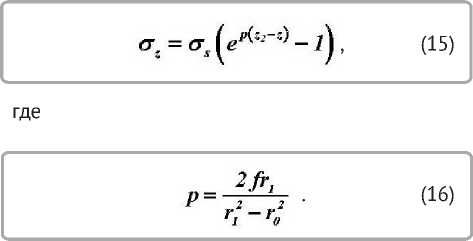
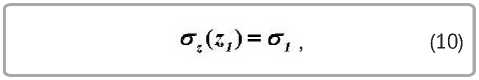
При подстановке z = z₁ получим напряжение на выходе из конической части матрицы:

где σ ₁ — осевое напряжение в выходном сечении конической части матрицы.

После упрощений получим следующую зависимость для распределения напряжений в конической части матрицы:

,

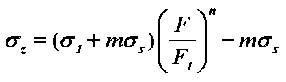
где F и F₁ – площади текущего и выходного сечений конуса, а m и n – коэффициенты, равные

1 f + tga m =--—

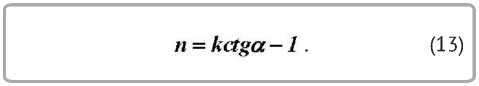
Распределение напряжений на цилиндрическом (калибрующем) участке матрицы можно определить из (6) при α = 0 и r = r1:

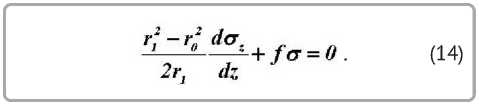
Подстановка в (14) σr = σ и условия пластичности (2) приводит к обыкновенному дифференциальному уравнению с разделяющимися переменными, решение которого при граничном ст, = CTs (eM^-m) _ ^ .        (17)

При конструировании матрицы необходимо задать ее геометрию таким образом, чтобы напряжение на входе в коническую часть матрицы оказалось равным значению критического давления p₀ , при котором материал становится несжимаемым (беспористым). Данная величина принимается по результатам экспериментальных исследований. Тогда из (11) при соответствующих подстановках можно найти радиус r₂ основания конуса экструзионной матрицы:

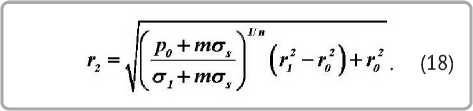
Рассмотрим пример расчета матрицы для экструдирования изделия в виде трубы с наружным диаметром 40 мм и внутренним диаметром 30 мм из пластифицированного бронзового порошка.

Выявим геометрические данные, определяемые экструдируемым изделием: радиус дорна r₀ = 15 мм, радиус калибрующей части матрицы r₁ = 20 мм.

Назначим длину калибрующего участка матрицы z₂ – z₁ = 25 мм, а угол конуса калибрующей части примем равным α = 30⁰ .

Согласно изложенной выше методике, для выбранного материала необходимо измерить три величины, определяемые его свойствами: критическое давление p0, при котором материал становится несжимаемым, а также соответствующие этому давлению предел текучести σs и коэффициент внешнего трения f. Методика и результаты измерений этих показателей приведены в [4, 5] и в данной работе не рассматриваются. Для бронзового порошка, пластифицированного парафином, принимаем p0 = 60 МПа, σs = 12 МПа, f = 0,13.

По формулам (16), (7), (12), (13) определяем значения коэффициентов: p = 0,03 мм^-1, k = 0,76 , m = 4,08 , n = 0,33 . Теперь по зависимостям (17) и (18) соответственно найдем давление на выходе из калибрующего участка σ ₁ и радиус на входе в конический участок матрицы r₂:

а₁ = 13,22 МПа, г₂ = 34,78 мм. (19)

Результаты расчетов показали, что при проектировании экструдера для заданных условий можно принять входной диаметр конусной части матрицы равным 70 мм. Этому же значению будет равен наружный диаметр шнека.

На втором этапе проектирования необходи- мо определить оптимальные геометрические характеристики силового шнека экструдера. Схема процесса уплотнения материала в канале шнека показана на рисунке 2.

Материал перемещается по каналу 2 от бункера к матрице 1. Движущая сила возникает из-за трения среды о подвижную поверхность шнека и давления p(z₀) = p_в на входе в канал. Ось z направлена против движения материала от выхода канала к его входу (от матрицы к бункеру). Начало отсчета совпадает с границей раздела между каналом и матрицей, давление в этой точке, равное p(0) = p₀ , определяется только свойствами среды и геометрией матрицы.

Деформация находящегося в канале шнека материала сопровождается его уплотнением. Поэтому, в отличие от (5), связь между касательными и нормальными напряжениями будем определять нелинейным законом трения:

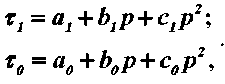
где τ ₁ и τ ₀ – касательные напряжения на подвижной и неподвижной поверхностях; p – давление среды на стенки канала, являющееся функцией

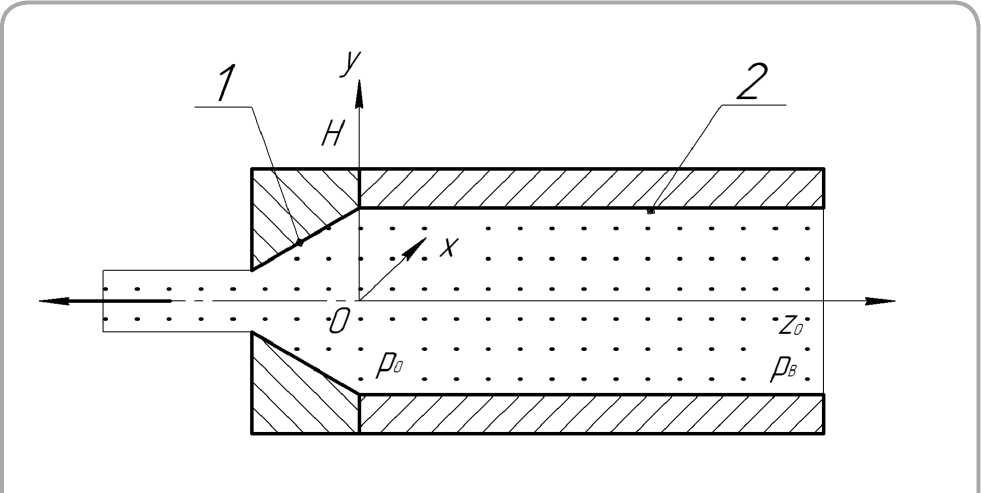
Рисунок 2 – Схема процесса уплотнения материала в канале шнека

г

координаты z ; a₁ , b₁ , c₁ и a₀ , b₀ , c₀ — инвариантные к напряжениям коэффициенты, характеризующие трение материала о подвижные и неподвижные поверхности канала.

Приращение силы трения dF_mp среды о стенки канала при увеличении координаты z на величину dz связано с приращением давления dp следующим образом:

X.

dF_mp = -2Sdp = -2^^ - T_ol_o)dz ,  (21)

где 2S – площадь поперечного сечения канала; 2l₁ и 2l₀ – части профиля, принадлежащие подвижной и неподвижной поверхностям соответственно.

Задача нахождения распределения давления вдоль канала сводится к решению обыкновенного дифференциального уравнения с разделяющимися переменными

dp = (jt-V bp-V cp^: )d^ ,        (22)

где коэффициенты a , b и c определяются трением и геометрией канала:

.

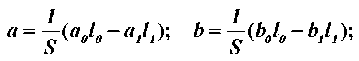
Л

.

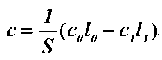
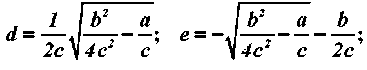
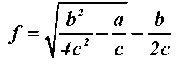
Постоянная интегрирования A находится из граничного условия p(0) = p₀ . Учитывая граничное условие p(z₀) = p_в , где p_в – давление на выходе из канала, создаваемое только силой тяжести, получим выражение для длины канала шнека, необходимой для создания в матрице требуемого давления p₀ :

7,_o = d\^^{Po eXf PgH}^ , ■     V - PoXpgH - e}

где ρ – насыпная плотность материала; g – ускорение свободного падения; H — глубина канала.

Зная длину и выбрав угол подъема канала шнека γ , можно определить длину нарезки шнека по формуле

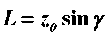
и соответствующее ей число витков

J

В частном случае, для канала прямоугольной формы

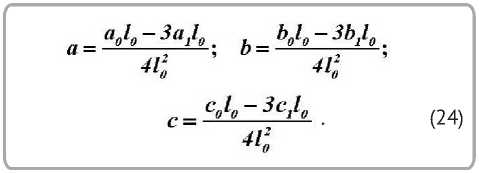
Решение уравнения (22) имеет вид

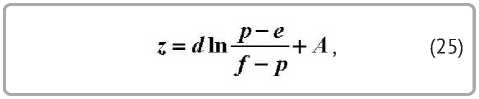
где

Рассчитаем параметры шнека с каналом прямоугольного сечения для получения рассмотренного выше изделия. Радиус шнека r₂ определен при расчете матрицы (19), принимаем r₂ = 35 мм; из предыдущего расчета известно также значение давления на выходе из канала шнека, оно равно давлению на входе в коническую часть матрицы: p₀ = 60 МПа.

Назначим следующие конструктивные параметры шнека: глубина канала H = 5 мм, угол подъема витка шнека γ = 22,5⁰ , значения l₀ половина ширины канала) и l₁ (половина профиля канала) составят соответственно 2,5 и 7,5 мм.

Для выполнения расчета необходимо измерить триботехнические характеристики a₁ , b₁ , c₁ и a₀ , b₀ , c₀ из параболического закона трения (20), а также насыпную плотность материала ρ .

Методика измерения этих показателей в данной статье не рассматривается. По данным [4], для выбранного материала измеренные значения будут равны: a₀ = 0,07 МПа, b₀ = 0,06 , c₀ = – 0,005 МПа^-1; a₁ = 0,02 МПа, b₁ = 0,2 , c₁ = – 0,006 МПа^-1.

По формулам (24), (26) находим коэффициенты: a = 0,001 , b = 0,006 , c = 0,0013 , d = 821 , e = – 4,44 , f = – 0,173 .

Теперь по (27) можно определить длину канала шнека: z₀ = 2607 мм. В соответствии с (28) и (29), этому значению будет соответствовать длина нарезанной части шнека L = 997 мм ≈ 1 м при n = 11 витках.

В современной практике конструирования для выполнения расчётов и разработки конструкторской документации широко применяются трехмерные CAD-системы. Имеющийся базовый функционал таких систем позволяет автоматизировать множество операций, непосредственно связанных с геометрическим моделированием и получением на основе построенных моделей ассоциативных чертежей. С целью автоматизации расчетов и построений по приведенным выше методикам разработано прикладное приложение [6], интегрированное в систему автоматизированного проектирования Компас-3D. Разработанное приложение содержит базу данных измеренных триботехнических и реологических констант для ряда материалов, выполняет расчеты геометрии формующего инструмента и шнека, а также позволяет автоматизировать ряд операций, связанных с разработкой трехмерных моделей и подготовкой конструкторской документации при проектировании экструдера.

Таким образом, разработанные методики расчета позволяют проектировать шнековые машины для экструзии пластичных сред с оптимальными геометрическими параметрами экструзионных матриц и силовых шнеков, а реализация этих методик в виде прикладной САПР позволяет сократить время на подготовку трехмерных моделей и выпуск конструкторской документации.