Методика рационального выбора состава резервных каналов связи в интересах повышения устойчивости информационно-телекоммуникационной сети с учетом результатов воздействия противника

Вводные замечания

В общем случае задача определения структуры резервных каналов связи может быть сформулирована следующим образом.

Известны:

– эффективность элементов узла связи телекоммуникационных систем (УС ИТКС);

– устойчивость элементов УС;

– вероятные маршруты закладки кабельных линий связи между отдельными УС ИТКС, их протяженность и стоимость (за единицу длины);

Методика рационального выбора состава резервных каналов связи ...

– стоимостные характеристики единовременных затрат на организацию дополнительных (резервных) каналов связи между i -м и j -м УС (С _ijo );

– вероятности вывода из строя отдельных элементов ИТКС в результате воздействия противника;

– список возможных резервных каналов (УС и линий связи) связи для каждого УС ИТКС { X_Pj , j= 1, n }.

Необходимо определить такой вариант оптимального выбора резервных каналов связи { Х доп } с { X_j , j = 1, n } из множества допустимых, который обеспечивает выполнение решаемых задач ИТКС с вероятностью (в смысле безошибочности и своевременности) не ниже требуемой с учетом воздействия противника при минимуме приведенных эксплуатационных затрат на организацию дополнительных линий связи:

^аоп ^^^^(®>5С-L. Х„ + С_ЦОХ, ) > min                   (1)

<=i при условии

P_i (УС) ≥ Р _зад; ∀ i , i = (1^—, n )                             (2)

X = ij

1 если i-й и j-й УС соединяются дополнительной линией связи, 0 в противном случае, где Рi (УС) – вероятность безошибочной и своевременной передачи информационного потока i-м УС с учетом воздействия противника.

Логико-вероятностный метод решения задачи

Решение задачи (1), (2) требует определения функциональной связи вероятности безотказной работы ИТКС между i -м и r -м УС от вероятности безотказной работы в процессе функционирования ИТКС элементов r -го УС. Предложенные в [8–12] методы решения этой задачи трудоемки и во многих случаях обеспечивают лишь квазиоптимальное решение.

Предполагается для определения этой функциональной зависимости использовать логико-вероятностный метод, реализованный при помощи процедуры ортогонализации структурной функции сети.

Рассмотрим граф G , в котором узлы соответствуют отдельным УС ИТКС, а ребра – линиям связи. Состояние сети описывается структурной функцией сети, принимающей значение 1, если между i -м и j -м УС существует связь, и 0 – в противном случае.

f_ij = f ( x ₁, x ₂,… x_n ),V i , j = 1, n ,                                    (3)

где x_i =1, если i -й элемент сети работоспособен, и x_i = 0 – в противном случае.

В дизъюнктивной нормальной форме (ДНФ) функция примет вид fij = ⋁ nm=1[⋀rμ=1Xδμμ]j,                                     (4)

где m – число простых путей из вершины i в вершину j ; r – ранг элементарной конъюнкции простой цепи графов;

δ_μ^G {0,1}; X _μ⁰ = X _μ; X ¹_μ = X_μ .

128 и нформационная безопасность

В [7, 8] показано, что дизъюнктивная нормальная форма (ДНФ) (4) может быть представлена в виде покрытия П кубического комплекса L . Каждой элементарной конъюнкции К _i (4) ставится куб, цена которого равна рангу r элементарной конъюнкции. В [6] показано, что для определения вероятности безотказной работы ИТКС между i -м и j -м УС сети в случае статистической независимости отказов элементов необходимо найти структурную функциональную сеть, выраженную в минимальной ортогональной дизъюнктивной нормальной форме (ОДНФ).

Знаком # обозначена #-операция, являющаяся некоторым видом операции вычитания кубов. Координатная #-операция приведена в таблице.

Координатная #-операция

a	b
	0	1	X
0	Z	Y	Z
1	Y	Z	Z
X	1	0	Z

Допустим, что рассматривается два куба – C_s ( a ₁, a ₂, …, а_n ) и С ₂( В ₁, В ₂, ..., B_n ), тогда #-операция определится следующим образом [2]:

C_s , если _i ( a_i , # b_i = y ) i = 1, n ;

C # C = s z

0, если _i ( a_i , # b_i = z) i =1, n ;

( a ₁,…, a_{i -1}, a_i , a_{i +1},…, a_n ), a_i # b_i = α_i ;

a е {0,1}, и это объединение производится по всем i . Справедливы следующие свойства #-операции:

CS # СZ = Cs, если СS – CS = 0;(6)

CS # CZ = 0, если CS – CZ;(7)

CS # СZ – CS.(8)

Обозначим кубы, принадлежащие покрытию П( L ) структурной функции сети, через C_S , а кубы, принадлежащие покрытию П₀( L ) структурной функции сети, выраженной в минимальной ОДНФ, – через C_S^o . Очевидно, что справедливо равенство

П(L) = ⋃vm=1Cv = ⋃vm=1(a1v,av2,…, avn),(9)

где C_v = 1, m – куб, соответствующий элементарной конъюнкции К _v совершенной формы (СФ) рассматриваемой сети.

В том случае если из графа, определяющего структуру ИТКС, исключить один из его элементов, то структурная функция, выраженная в виде покрытия П – кубического комплекса L , примет следующий вид:

• а) в случае исключения ребра k

П _k ( L )= ⋃ _v ^m ₌₁ ( a _{1 k} ; i = 1, n ),                              (10)

Методика рационального выбора состава резервных каналов связи ...

где

v aik =

0, Vi =1, n если avv =1, n =1, m;

0, если a" = X, i = 1, n, n=1, m;

б)

в случае исключения вершины q

П ( L ) = ⋃ ^m ( a^v ) i = 1, n ,                           (12)

{kq}               v=1 i{kq} где {kq} – множество ребер {kq}, принадлежащих вершине.

Из (10) и (11) видно, что операция исключения (11) является общим случаем. Обозначим операцию исключения ребра следующим образом:

П (L) = П(L); v = 1,m. kv ak

Методика применения метода

Для иллюстрации методики рассмотрим пример. Структура ИТКС состоит из главного центра связи (ГЦС) и подчиненных ему УС и имеет вид, как на рисунке. Необходимо найти вероятность достоверной (то есть безошибочной и своевременной) передачи информации из УС № 3.1 в УС № 3 в случае:

• 1)    наличия связи между УС № 3.1 и УС № 3.4;

• 2)    ее отсутствия.

  

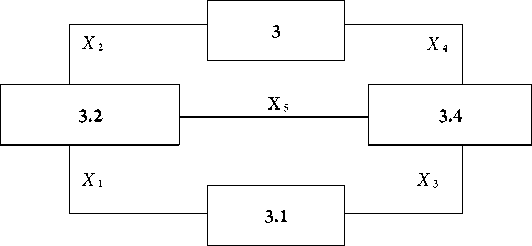
  Фрагмент графа сети связи структурных подразделений системы управления

  
  

Структурная функция сети для случая наличия связи f13 = x3 x4 Vx1 x2 Vx1 x5 x4 Vx3 x5 x2.

Ортогональную дизъюнкцию нормальной формы найдем с помощью алгоритма ортогонализации, рассмотренного выше:

получим

	X	X	1	1	X		1	1	0	X	X
	1	1	X	X	X		1	1	X	0	X
n( L )=П1=-	1	X	X	1	1	■; П 2 = П 1 # С 1 = ■	1	X	0	1	1	и т.д.,
	X	1	1	X	1		X	1	1	0	1

Информационная безопасность

X X 1 lx 1 1 0 x x П0( L ) =■ 1   1   1 0 X . 0 110 1 10 0 11 Для получения П0k(L) воспользуемся свойствами операции исключения элемента av3 (n = 1,5)

-I—г       -I—г             11 х х

П об(L )=По (L )/^=11 0 1 1

Для определения структурной функции межуровневой сети связи рассмотрим граф, вершины которого обозначают УС, а дуги – все возможные связи (в том числе и предполагаемые дополнительные). Тогда, поставив в соответствие исходной сети G_i,_g , где g -номер УС – матричное число совокупность простых путей из вершины i сети в вершину g – может быть определена по формуле

( Q. Y ^} y = i,2,.. = {d ^et" [ ^а jj ] J, ^j = q ; ^£ =1, ^{, ,} mod2

где { Q^T_O q } _T =_1|2,_ – множество простых путей сети из вершины I в вершину q ;

det" [a jj ]mod2 = Z-n[det eij ]mod2 1∈s 1∈n есть модифицированная детерминантная функция прямой производственной матричного числа по индексам; Lij – элементы матричного числа α; n, s – число строк и столбцов контурного числа сети G; γ – номер простых путей графа G во множестве {Qξqγ}; ∑ – знак логического сложения полученных столбцов детерминантной функции.

Обозначим через {X _ij } множество всех допустимых (возможных) дополнительных линий связи для каждого из i = 1, n УС ( ij = 1, n ) . Тогда с учетом существующих линий связи для каждого i может быть определен комплекс минимального ортогонального покрытия П_{o i} ( L ) i = 1, n по изложенному выше алгоритму ортогонализации.

По имеющемуся выражению П_{о i} ( L ) может быть определено выражение для оценки устойчивости функционирования i -го УС и старшего УС вышестоящего уровня при структуре линий связи x ⁰ _ij ( i,j = 1, n ), то есть P_{i (УС)} ( x ⁰ _ij ) → П_{о i} ( L ).

Запишем П_{о i} ( L ) в виде П_{о i} ( L ) = l_v , где l_v – элемент комплекса минимального ортогонального покрытия сети связи i -го УС со старшим УС вышестоящего уровня, соответствующий х -му элементу v -гo куба элементарной конъюнкции C_v комплекса П_{о i} ( L ); v = 1, m ; ӕ = 1,μ. Здесь через μ _i обозначим число всех связей, обеспечивающих связь i -го УС со старшим УС. В свою очередь, множество связей может быть представлено в виде объединения { X } = { X ⁰} { X _{1 ∅} }, где множество { X ₀} означает множество вводимых дополнительных связей, а множество <Хе> – множество имеющихся связей. В связи с тем, что нумерация элементов lv ӕ в комплексе ортогонального покрытия П_{o i} произвольна, обозначим X {Х°} номерами X ⁰ = l , μ_oi , а Х ₁ = (μ_o + 1).

Методика рационального выбора состава резервных каналов связи ...

Тогда

Поi(L) = lv1, lv2,…, lvμoi + 1,…, lvμi, v = lСmi, где lvμoi + 1, μ представляют собой совокупность варьируемых связей i-го УС со старшим УС (i = 1).

Естественно, что каждому l v ( v = 1, m ; = 1, ^ ) может быть поставлено в соответствие некоторое значение β, то есть l _β βV v = 1, m_i при условии, что тогда, учитывая однозначное соответствие между комплексом минимального ортогонального покрытия П и вероятностью связи i -го УС и старшего УС и предполагая, что отказом всех видов подвержены только линии связи, условие может быть переписано в виде

2Х „. = И в X . ^ min; i = 1              1 = ^o 1 + 1

P ( УС )

П ( L ) о г

> >  P , v = 1, m ; z = 1, n , зад'        ' ’         ⁷ П

I {lv 1 X1} где Поi (L)/{lv1X1} означает последовательное выполнение операции исключения элементов lv1X1 из комплекса кубов Пiо(L);

X ₁ =

• 1,    если связь 1 вводится, 0 в противном случае

X ₁₌₁ – X ₁.

Этапы определения рационального количества резервных каналов связи

Таким образом, для определения рационального количества резервных каналов связи с целью обеспечения устойчивого функционирования ИТКС в условиях воздействия противника необходимо выполнить следующие этапы.

• 1.    Присваиваем i = i + 1.

• 2.    Составляем граф полной сети G_i i -го УС с соответствующим старшим УС, включая в него как существующие, так и предполагаемые линии связи.

• 3.    Определяем значение структурной функции сети связи i -гo УС, пользуясь выражением.

• 4.    Выполняем алгоритм ортогонализации для получения ортогональной дизъюнктивной нормальной функции СФ i -го УС.

• 5.    Проверяем i = n , где n – общее количество УС; если да, то переходим к пункту 1.

• 6.    Разграничиваем множество связей на два подмножества:

• a)    — { X ¹ } 1 - подмножество вводимых дополнительных связей;

• б)    U { X o ) 1 – подмножество имеющихся линий связи.

• 7.    Для каждого элемента подмножества { X ¹ } 1 , i = 1, n рассчитываем значение стоимости организации линии связи.

• 8.    Ранжируем элементы множества — { X ¹} 1 .

• 9.    Исходя из эвристических соображений определяем множество предпочтительных линий связи, вводимых в общую структуру сети.

• 10.    Решаем задачу оптимизации. По найденному оптимальному решению составляем список дополнительных линий связи абонентской сети и список абонентов каждой линии связи.

132 и нформационная безопасность

По полученному таким образом множеству связей определяем значение функционала, которое в дальнейшем рассматривается как дополнительное ограничение в задаче оптимизации.

Выводы

Разработанная методика позволяет решить комплексную задачу структурного резервирования ИТКС с распределенными территориально УС и линиями связи, подверженными воздействию противника, учитывающую специфику функционирования УС как элементов общей сети. Она чувствительна к изменениям параметров, определяющих структуру технологического потока обработки информации в отдельных УС, а также к характеристикам различных вариантов ее функционирования. Поэтому данная методика позволяет оперативно проводить реорганизацию ИТКС в соответствии с изменениями номенклатуры технических средств решения задачи или с изменениями средств воздействия противника.