Методика расчета изменения давления в цилиндрических полостях для исследования истечения продуктов детонации при взрыве удлиненных зарядов ВВ в шпурах и скважинах

Повышение эффективности проходки подземных горных выработок буровзрывным способом является одним из приоритетных направлений развития горного производства.

При использовании забойки в буровзрывных работах (БВР) наиболее важным является обеспечение достаточно длительную задержку снижения давления продуктов детонации (ПД) в шпурах (скважинах), при которой происходило бы надежно формирование квазистатических полей напряжений и соответствующее разрушения горных пород.

Несмотря на имеющиеся теоретические и эмпирические соотношения для определения рациональных видов забойки не всегда учитывается ряд факторов:

• -    свойства материала забойки, ее распор, влияние направления инициирования на движение забойки, изменение давления в шпуре по мере истечения ПД и т.п.

В то же время, обобщённые соотношения на основе многофакторных экспериментов громоздки и неудобны для практических расчетов, причем влияние отдельных факторов неоправданно занижено или не учитывается совсем. Кроме того, до настоящего времени не существует обобщённой теории влияния типов забойки, ее движения и истечения ПД на эффективность взрыва удлиненного заряда в шпурах (скважинах). Теоретические оценки влияния забойки на эффективность разрушения породы взрывом никак не связаны с формированием полей напряжений и процессам разрушения пород взрывами зарядов ВВ. Нет четкого представления о методах определения параметров истечения ПД, кинематики движения забойки и их взаимосвязи с формированием полей квазистатических напряжений в породе, разрушаемой взрывом.

Для определения параметров истечения ПД необходимо проинтегрировать систему одномерных нестационарных уравнений газовой динамики с учетом граничных условий. Соответствующие уравнения газовой динамики в Лагранжевой системе координат при наличии потерь кинетической и потенциальной энергии принимают вид:

• -    сохранение момента количества движения

  du dt

  
  

  d(p+q) du \u l

  
  

  dh

  
  

  2d

  
  
  
  

Сохранение массы

• 1    — dL p dh

  
  

Сохранение энергии de dt

du du lul у Р Т-Т о

------ dh    2d у-1 Т Р Г

где:

е= C v T; — = и;

е-внутренняя энергия, Дж/моль;

Сv –удельная теплоёмкость при постоянном объёме, Д/(К*моль)

r- эйлеровский радиус, м;

t- время, с;

p,u,v.T- давления , скорость, удельный объём и температура ПД, Па, м/с, м3/кг, К;

q-искусственная вязкость, Па;

γ-отношение удельный теплоёмкостей, в общем случае зависящее от текущего значения плотности газовой смеси;

h- лагранжевая координата;

λ-коэффициент трения о внутреннюю поверхность шпура;

d-диаметр шпура, м.

Левое граничное условие соответствует случаю газонепроницаемой стенки, т.е. величина массовой скорости и на левой границе всегда с течением времени принимает значение, равное О. Граничное условие на срезе шпура записывается в виде дополнительного слагаемого в уравнении (1), характеризующего сопротивление ПД на срезе при их сверх звуковом истечении:

^^ = k₀(p-p₀)                      (4)

где: k₀ -коэффициент пропорциональности, определяемый количеством газа, вовлекаемого в движение внутрь шпура волной разрежения (величина к₀ предполагается неизменной);

р₀ -атмосферное давление, Па.

Для аппроксимации уравнений газовой динамики использовалась конечноразностная, условно-устойчивая схема типа "крест" с. искусственной вязкостью.

Предложенная численная методика предлагается при решения задачи теории сильного точечного взрыва и для расчета избыточного давления, возникающего в цилиндрической полости, при взрыве газовых смесей. При этом предложенная последовательность численного моделирования обеспечивает величину относительной погрешности не более 15% по сравнению с аналитическими и экспериментальными данными (табл.1), что и позволит применить эту модель для исследования истечения ПД при взрыве удлиненного заряда ВВ.

Таблица 1

Распределение скорости и плотности за фронтом ударной волны при сильном точечном взрыве в воздухе при Е взр =5*10³Дк

r/r ув		0,9	0,8	0,5	0,3
V Vye	т.р	0,86	0,63	0,42	0,24
	ч.р.	0,95	0,55	0,48	0,27
	d,%	+10,5	-12,7	+14,3	+12,5

р Р ув	т.р	0,52	0,18	0,06	0,015
	ч.р.	0,55	0,2	0,07	0,013
	d,%	+5,8	+11,1	+16,6	-13,3

Однако на процесс разрушения порода взрывом оказывают существенное влияние физико-технические параметры забойки (длина, плотность, материал, коэффициент трения и т.д.) и теоретическая оценка этих факторов требует значительных трудовых и материальных затрат.

Теоретически возможно установить, что время Т 1 , в течение которого происходит вывод забойки из неподвижного состояния, определяется тем, что начало перемещения различных частей забойки происходит постепенно по мере вовлечения их в движение и, следовательно, перемещение забойки как целого начнется только после того, как продольная волна сжатия пробежит по ее длине по крайней мере 3-4 раза.

В качества базисных параметров для рассматриваемого процесса приняты 1, р₃, С_р так, что следуя -теореме теории подобия и размерности, время т 1 может быть представлено в виде некоторой зависимости:

^гГиЛ-Ц-ЛД-^ЛУс.         (5)

• ¹     С р       , , ^q - , р₃ , i , p₃q - , i '                            ⁽ )

где, учитывая характер данного процесса, была введена величина 1ша h -толщина пограничного слоя. Максимальное значение h не превышает 5d ч, которое и было принято за основу. При сделанных допущениях и физической сущности рассматриваемого явления отношения d /1 и h /1. постоянны в течение всего времени T 1 и поэтому зависимость (5) от них дальше не определялась. После математической обработки экспериментальных данных зависимость (5) выглядит следующим образом:

Т1 = 3,761^(1 + 9,48^(1 + 8,44* 10-5^|p)      (6)

Процесс движения забойки по шпуру определяется законами сохранения энергии и импульса с учетом потерь на трение:

для сплошной забойки m3dX. = Sp(1-8),                       (7)

где S- площадь поперечного сечения шпура, м2;

Р- давление в ПД;

8 - коэффициент трения скольжения (для дерева и свинца 8 равен *0,45 и 0,1 соответственно).

для сыпучей забойки – dx2 _ [1-к*(1-х)]Р dt2 =      61     ,

где к*- удельная величина коэффициента трения (для песка-0,86 м-1);

• I-    длина забойки,м;

в -удельный вес материала забойки (для песка 0=1600 кг/м³).

Решением дифференциального уравнения (8) является интегральная кривая, уравнение которой с начальными условиями х(0)=О выглядит следующим образом:

S(1-6»)Pt² х = -------- , м,

т3

а решением уравнения (9), удовлетворяющему тем же начальным условия является зависимость t(x):

^ 2 = Jpin|

2(х) + ^(х) + 1|,с;          (10)

*„

(р(х) = 7—7?;0 < X < 1 .

1-к * 1

При этом изменение давления Р в шпуре, обусловленное расширением ПД, рассчитывается по следующей формуле:

^Р=Р 1 {£ЬГ    (1¹)

^ 1ТХ/

Где:   Р 1 - давление, установившееся после начала движения забойки;

у - показатель изоантропы ПД.

Для установления обобщающих закономерностей истечения ПД рассматривался безразмерный критерий подобия / в области сверхзвукового течения газа в соответствии с законом сохранения количества движения с привлечением результатов численного расчета свободного истечения:

У =----, (12)

PiOi+aroiani v ’ где:

n ^au= MZp i^(ui i-1

— и—^м

n

= ^PiM;

i-i

Ti-текущее значение Эйлеровой координаты, соответствующее J-му слоев времени, м;

At₁ -приращение координаты за промежуток At = V — t^i-1, м;

P i -усреднённое значение плотности газовой смеси, заключённой между дном шпура и сечением с координатой г₁ , кг/м³;

В результате анализа (12) определена общая зависимость времени истечения ПД в произвольном сечении шпура при взрыве в нем удлиненного заряда ВВ от безразмерных параметров ае, п и времени детонации t, которая принимает следующий вид:ю

т3 = t0 {1.1719 [1 + ^2] + 3 3.3 6ж2 — 6 0.0 8с + 2 6.72} + 2-2,   (13)

где х - расстояние от устья шпура до исследуемого сечения, м;

N - число репарных точек;

• L - длина шпура, м;

• c - скорость звука в ПД, м/с;

• n = 1+N; n= n/N; 1 < с < 2.

Р = 4 , Па. ж^

Полученные зависимости (6)+(14) с достаточной для практики точностью в пределах 15% величины относительной погрешности позволяют определить динамику движения забойки и истечения ПД из шпуров.

При рациональном материале забойки, способная обеспечить задержку истечения ПД из шпура по крайней мере в области, прилегающей к его устью, на величину т1 (время квазистатического нагружения ГП взрывом), в результате чего будет практически полностью реализована потенциальная возможность взрыва удлиненного заряда на максимальное обеспечение формирования зоны мелкодисперсного дробления до величины, позволяющая сформировать около заряда квазистатическое поле напряжений. Величина Т1 : определяется по процессу деформирования ГП в ближней к шпуре зоне при камуфлетном взрыве заряда удлиненного ВВ, согласно теории проф. В.Н. Родионова (рис.1).

Рассмотреная численная методика расчета изменения давления в цилиндрических полостях конечной длины за счет истечения ПД из полости обеспечивает величину относительной погрешности не более 15%, что позволяет применить эту модель для исследования истечения ПД при взрыве удлиненных зарядов ВВ в шпурах и скважинах.

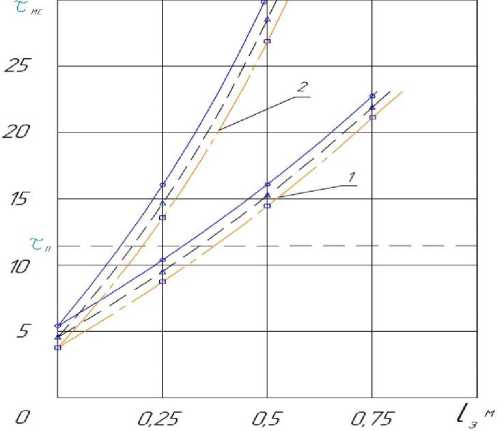
Рис.1. Зависимость времени спада давления в различных сечениях шпура от материала забойки при взрыве AM №6 ЖВ в песчанике.

1- забойка из песка; 2 - взрывная запрессовка устья шпура.

На основании выше приведенного можно сделать вывод что с применением забойки процесс истечения ПД из модели происходит в три этапа:

- на первом этапе длительностью Т 1 происходит вывод забойки из неподвижного состояния под действие упругих волн, генерируемых в ней ПД;

- на втором этапе длительностью т2 имеет место движения забойки из шпура;

-на третьем этапе происходит квазистационарное истечение ПД длительностью т3, который, в свою очередь, подразделяется на два этапа:

Во время первого этапа длительностью т 1 . наблюдается распространение особой волны разрешения по ПД от устья шпура с резким скачкообразным уменьшением давления, во время второго этапа длительностью т₂ наблюдается квазистациойарное истечение ПД из шпура с постепенным уменьшением в нем давления.