Методика расчета магнитной цепи синхронной явнополюсной машины с использованием конформных отображений

Омский государственный университет путей сообщения, г. Омск, Россия; e-mail: , ORCID:

Повышение энергетических показателей явнополюсной синхонной машины, уменьшение вибрации при ее работе может быть достигнуто за счет оптимизации полюсных наконечников и обеспечения синусоидальной формы кривой распределения магнитной индукции в воздушном зазоре. Предложена методика для расчета магнитной цепи синхронной явнополюсной машины с использованием конформных отображений. Методика включает в себя два метода – метод конечных элементов и метод конформных отображений. Для расчета магнитной цепи электрической машины на пару полюсов рассматривается магнитная цепь прямоугольной формы, для которой методом конечных элементов осуществляется решение полевой задачи. Метод конформных отображений позволяет преобразовать прямоугольную область в сектор, соответствующий магнитной цепи машины на пару полюсов, и определить напряженность и индукцию магнитного поля в различных точках этой области. По известным значениям напряженности и индукции магнитного поля в различных точках сектора магнитной цепи на пару полюсов эти векторные величины можно рассчитать для других полюсов машины. Для конформного преобразования прямоугольной области в область, соответствующую сектору магнитной цепи синхронной машины на пару полюсов, применена показательная функция. В качестве примера использования разработанной методики выполнен расчет кривых нормальной и тангенциальной составляющих магнитной индукции в воздушном зазоре на пару полюсов для шестиполюсной и восьмиполюсной синхронных машин с учетом неравномерного воздушного зазора между полюсным наконечником и сердечником статора. Для проверки результатов расчетов магнитное поле сектора магнитной цепи машины рассчитано также методом конечных элементов в пакете программ FEMM. Выполнено сравнение кривых нормальных (тангенциальных) составляющих магнитной индукции в воздушном зазоре, рассчитанных по предложенной методике и с использованием FEMM. Относительная наибольшая погрешность не превышает 0,47 %. Москалев Ю. В. Методика расчета магнитной цепи синхронной явнополюсной машины с использованием конформных отображений. Вестник МГТУ. 2025. Т. 28, № 4/1. С. 522–531. DOI:

e-mail: , ORCID:

Moskalev, Yu. V. 2025. A method for calculating the magnetic circuit of a synchronous salient pole machine using conformal mappings. Vestnik of MSTU, 28(4/1), pp. 522–531. (In Russ.) DOI:

Синхронные машины с электромагнитным и магнитоэлектрическим возбуждением используются в различных отраслях промышленности и на транспорте в качестве генераторов и двигателей. Синхронные генераторы являются источниками электрической энергии, которая вырабатывается на мощных электростанциях различных типов (тепловые, гидро-, ветряные) дизель-генераторными установками. Синхронные двигатели часто применяют в приводах большой мощности1.

Улучшение массо-габаритных показателей, показателей энергоэффективности и надежности, снижение материалоемкости при проектировании и изготовлении синхронных машин обеспечивается за счет использования новых материалов активной части, новых электроизоляционных материалов, оптимизации конструктивных элементов магнитной цепи машины с учетом режимов ее работы и регулирования реактивной мощности.

В синхронных машинах магнитное поле имеет несинусоидальную форму, характер распределения этого поля зависит от ширины и конфигурации полюсного наконечника, от относительной длины воздушного зазора2. Улучшение энергетических показателей явнополюсной синхонной машины, уменьшение вибрации при ее работе может быть достигнуто за счет оптимизации полюсных наконечников и обеспечения синусоидальной формы кривой распределения магнитной индукции в воздушном зазоре.

Для расчета магнитных цепей электрических машин используют различные методы, которые предполагают решение полевых задач и (или) анализ схем замещения³ ( Афанасьев, 2022 ). При расчете магнитных полей синхронных машин также находит применение метод конформных отображенинй ( Афанасьев, 2022; Афанасьев и др., 2016; Майоров, 1999; Шакиров и др., 1998; Шевченко и др., 2018; Boughrara et al., 2010; Ding et al., 2023; Hafner et al., 2010; Hanic et al., 2016; Jansen et al., 2022; Olivio et al., 2016; Tikellaline et al., 2017; Yang et al., 2025 ). Это позволяет упростить решение полевой задачи за счет преобразования заданной области с помощью конформного отображения в область более простого вида и наоборот⁴ ( Афанасьев и др., 2016 ).

Цель исследования – разработать подход к расчету и анализу магнитной цепи синхронной явнополюсной машины, использующий конформные отображения.

Теоретические основы

Для конформного преобразования прямоугольной области в область, соответствующую сектору магнитной цепи синхронной машины на пару полюсов, используем показательную функцию комплексного переменного w (z ) = az,                                                  (1)

где a – основание степени, a > 1; z , w – комплексные числа ( z = x + j · y и w = u + j · v ); j – мнимая единица.

На рис. 1 показана схема магнитной цепи прямоугольной формы на комплексной плоскости Z (рис. 1, а ), которая с использованием функции (1) преобразуется в сектор на комплексной плоскости W (рис. 1, б ), соответствующий магнитной цепи явнополюсной синхронной машины на пару полюсов.

При расчете магнитной цепи синхронной машины с использованием конформных отображений приняты следующие допущения: не учитывается нелинейность кривой намагничивания материала магнитной цепи, относительная магнитная проницаемость электротехнической стали принимается постоянной, магнитная цепь электрической машины – симметричная, сердечник статора принят гладким (без пазов).

При конформном отображении магнитное напряжение между близлежащими точками плоскости Z будет равно магнитному напряжению между соответствующими точками плоскости W :

Hdz = H_wdw ,                                (2)

где dz , dw – приращение на комплексной плоскости Z и W соответственно; H_z , H_w – напряженность магнитного поля на комплексной плоскости Z и W соответственно, А/м.

Зная напряженность магнитного поля области на комплексной плоскости Z можно вычислить эту векторную величину на комплексной плоскости W:

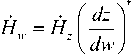
= H z

1-Ы ^ w In ( a )^

где ( dz / dw )* – сопряженный с dz / dw комплекс.

Также можно записать

(

( u ² + v ²) In ( a )     ( u ² + v ²) In ( a )

₄ w In ( a )

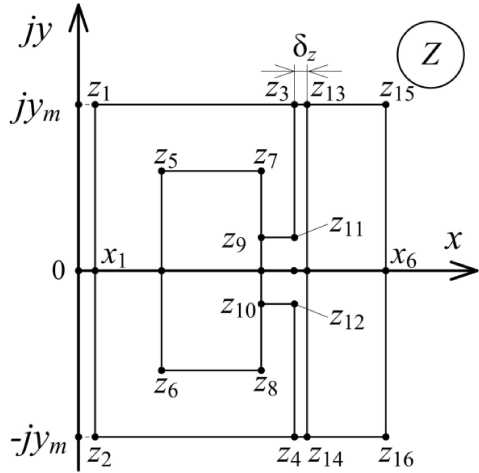
Рис. 1. Схема магнитной цепи для расчета магнитного поля синхронной машины на пару полюсов: а – схема прямоугольной формы на комплексной плоскости Z ;

б – сектор магнитной цепи электрической машины на комплексной плоскости W

Fig. 1. Magnetic circuit diagram for calculating the magnetic field of a synchronous machine for a pair of poles: a – a rectangular shape diagram on the complex Z plane; б – the sector of an electric machine magnetic circuit on the complex W plane

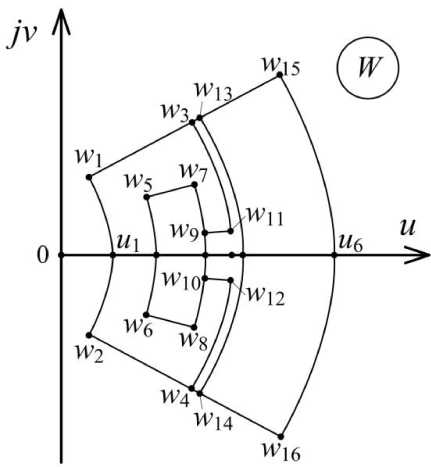
б

Действительная и мнимая части комплексной функции (1) равны u = ax cos (y In (a));

v = a^x sin ( y In ( a ) ) .

С учетом выражений (5) и (6)

*

w In ( a )

cos

sin

e j ^ln ( ^a )

a^x In ( a )           a^x In ( a )      a^x In ( a )    a'

x

ajy

In ( a)

В результате формулу (3) можно записать следующим образом: _a jy

w

z a^x In ( a )

Как известно, магнитная индукция и напряженность поля связаны через соотношение

B = h ^. rH,

где μ 0 – магнитная постоянная, Гн/м; μ r – относительная магнитная проницаемость материала сердечника.

С использованием выражений (8) и (9) можно с учетом принятых допущений вычислить напряженность и индукцию магнитного поля в любой точке сектора на пару полюсов магнитной цепи машины.

Выполним анализ распределения магнитной индукции синхронной машины в воздушном зазоре (вдоль внутренней расточки сердечника статора), так как форма этой кривой определяет закон изменения ЭДС в обмотке статора и влияет на различные показатели работы электрической машины5.

В точке z прямоугольной области (рис. 1, а ) нормальная H_z.n и тангенциальная H_z.t составляющие напряженности магнитного поля равны действительной и мнимой части комплексного числа H_z соответственно.

Благодаря этому формулу (8) можно записать следующим образом:

H w ( L t ) = H w . n ( L t ) + H w . t ( L т ) = H T^ a j + jH zr y^^a j ,                (10)

a In ( a )         a In ( a )

где H_z.n ( y ) и H_z.t ( y ) – действительная и мнимая часть комплексного числа, составляющие вектора напряженности магнитного поля H_z в заданной точке отрезка z ₁₃ – z ₁₄ области на комплексной плоскости Z (рис. 1, а ), А/м; L _τ – координата вдоль дуги внутренней окружности сердечника статора на полюсном делении τ, м

L т ( y ) = a x [ y ^ln ( ^a ) ^{+ П} ] .                                       ⁽¹¹⁾

\         ² p J

За нулевое значение координаты L _τ принята точка w ₁₄ L _τ = 0, в точке w ₁₃ переменная L _τ равна длине дуги вдоль внутренней окружности сердечника статора (рис. 1, б ).

Вектора нормальной и тангенциальной составляющих напряженности магнитного поля вдоль внутренней окружности сердечника статора на плоскости W (рис. 1, б ) равны соответственно

H w . n ( L т ) = HrA a j ;                                (12)

a In ( a )

H w. ( L т ) = jHTr\ a j .                                (13)

a In ( a )

Из расчетных выражений (12) и (13) можно видеть, что при заданных значениях x и a закон изменения модулей нормальной и тангенциальной составляющих напряженности магнитного поля вдоль внутренней окружности сердечника статора определяется законом изменения этих величин H_z.n ( y ) и H_z.t ( y ) вдоль отрезка z 13 – z 14 (рис. 1, а ).

Размеры прямоугольной области вдоль действительной оси зависят от заданных радиусов ( r_i ) элементов магнитной цепи (радиуса вала, ротора, внутренней расточки сердечника статора и наружного радиуса статора и других). Эти координаты прямоугольной области в именованных единицах можно определить по формуле

^X i = log a^r , •                                                        ⁽¹⁴⁾

Диапазон изменения мнимой части аргумента комплексной функции (1) зависит от показателя степени a и заданного количества числа пар полюсов машины p

I y | - У т = 7ГЙ •                                ⁽¹⁵⁾

• 2 p In ( a )

Методика расчета магнитной цепи синхронной явнополюсной машины включает в себя два метода – метод конечных элементов и метод конформных отображений. Метод конечных элементов необходим для решения полевой задачи для магнитной цепи прямоугольной формы на комплексной плоскости Z (рис. 1, а ). Метод конформных отображений позволяет преобразовать прямоугольную область в сектор, соответствующий магнитной цепи машины на пару полюсов, и определить напряженность и индукцию магнитного поля в различных точках этой области.

Исходные данные для расчета магнитной цепи синхронной явнополюсной машины:

• 1)    геометрические размеры магнитной цепи машины: радиус вала, внутренний радиус сердечника ротора ( r 1 = u 1 ); радиусы, соответствующие области для размещения обмотки возбуждения ( r 2 = u 2 и r 3 = u 3 ); радиус, соответствующий размеру полюсного наконечника ротора ( r ₄ = u ₄); внутренний и наружный радиусы сердечника статора ( r 5 = u 5 и r 6 = u 6 ), мм, где u i – координата по оси абсцисс на комплексной плоскости W (рис. 1, б );

• 2)    свойства материалов: относительная магнитная проницаемость сердечника (μ _r ), удельное сопротивление обмоточного провода (ρ, Ом·м);

• 3)    МДС обмотки возбуждения на полюс ( F , А) или плотность тока в этой обмотке ( J , А/м²).

Методика расчета предполагает выполнение следующей последовательности действий для расчета магнитной цепи машины с заданным числом пар полюсов p (любое натуральное число):

• 1)    решение полевой задачи для магнитной цепи прямоугольной формы методом конечных элементов (для решения этой задачи в статье использован пакет программ FEMM⁶);

• 2)    преобразование магнитной цепи прямоугольной формы в сектор магнитной цепи синхронной машины с использованием показательной функции;

• 3)    расчет напряженности и магнитного поля в заданных точках сектора магнитной цепи электрической машины на пару полюсов выполняется по формулам (8) и (9). Для расчета этих величин вдоль внутренней расточки статора можно использовать выражения (12), (13) и (9);

• 4)    вычисление напряженности и магнитного поля магнитной цепи для других полюсов синхронной машины.

Для того чтобы значения напряженности и индукции магнитного поля, плотность тока для магнитной цепи прямоугольной формы и сектора магнитной цепи были одного порядка по величине, нужно чтобы площадь сектора ( S w = (π r 6 ² – π r 1 ²)/(2 p )) и магнитной цепи прямоугольной формы ( S z = 2 y m (log a r 6 – log a r 1 )) были равны между собой S_z = S_w . Из этого равенства можно определить значение основания показательной функции (1) для заданных размеров магнитной цепи машины. Необходимо отметить, что значение основания функции a зависит от заданных радиусов элементов магнитной цепи машины и не зависит от числа пар полюсов p .

По известному значению напряженности H_w (8) магнитного поля в заданной точке w сектора магнитной цепи машины на пару полюсов эта векторная величина (с учетом того, что магнитная цепь машины симметричная) может быть рассчитана для других полюсов

Hw(k)=(-1)k-1 HwI expfj-(k- 1)H,(16)

ll P где Hw(k) – вектор напряженности поля в точке w(k) на комплексной плоскости W, А/м (k = 1…p).

Комплексная величина, соответствующая координатам точки, определяется по выражению w (k ) = w exp | j П (k -1)^.(17)

Рассмотренная методика может быть использована при анализе магнитной цепи явнополюсных синхронных машин с электромагнитным возбуждением различной мощности.

Результаты и обсуждение

В качестве примера использования предложенной методики выполним расчет распределения нормальной и тангенциальной составляющих магнитной индукции в воздушном зазоре синхронной машины для пар полюсов p = 3 и p = 4. Основание показательной функции (1) a = 1,027375.

Принятые для расчета геометрические размеры магнитной цепи машины и прямоугольной области, вычисленные по формуле (14), приведены в таблице.

Таблица. Заданные радиусы элементов магнитной цепи машины и координаты соответствующих элементов магнитной цепи прямоугольной формы по действительной оси комплексной плоскости Z Table. The specified radii of the machine's magnetic circuit elements and the coordinates of the corresponding elements of the rectangular magnetic circuit along the real axis of the complex Z plane

Наименование	i	u i = r i , мм	x i , мм
Радиус вала (внутренний радиус сердечника ротора)	1	10	85,259
Меньший радиус области ротора для размещения обмотки возбуждения	2	20	110,924
Больший радиус области ротора для размещения обмотки возбуждения	3	45	140,951
Радиус полюсного наконечника ротора	4	50	144,852
Внутренний радиус сердечника статора	5	51	145,585
Наружный радиус сердечника статора	6	75	159,865

Решение задачи выполнено для следующих исходных данных: относительная магнитная проницаемость сердечника ц r = 700, удельное сопротивление обмоточного провода р = 1/40 x 10 6 Ом^м⁷, МДС обмотки возбуждения на полюс F = 1 000 А. При a = 1,027375 размер магнитной цепи прямоугольной формы вдоль мнимой оси равен 2 y m = 38,775 мм ( p = 3) и 2 y m = 29,081 мм ( p = 4).

Для обеспечения необходимой формы кривой распределения магнитной индукции в воздушном зазоре машины полюсные наконечники изготавливаются со скосом8. В качестве примера при расчете принято, что часть полюсного наконечника (4/7 часть длины полюсного наконечника) имеет одинаковый воздушный зазор, равный 1 мм между сердечником статора и полюсом ротора. У края полюсного наконечника (3/7 часть длины полюсного наконечника) размер воздушного зазора линейно увеличивается до 2,55 мм на крайней грани полюса.

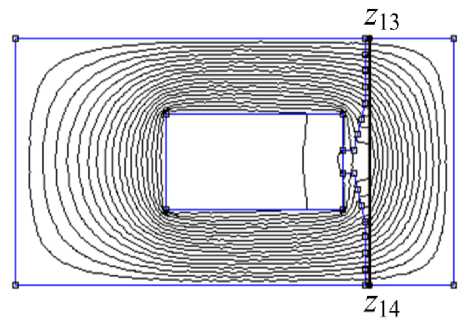
На рис. 2, а приведена расчетная схема магнитной цепи прямоугольной формы в FEMM, на рис. 2, б – результат расчета этой магнитной цепи при p = 3, I = 5 А, W = 200, J = 2,19 А/мм².

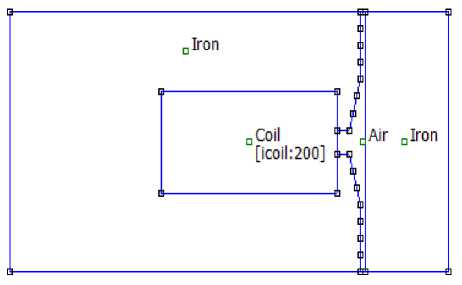
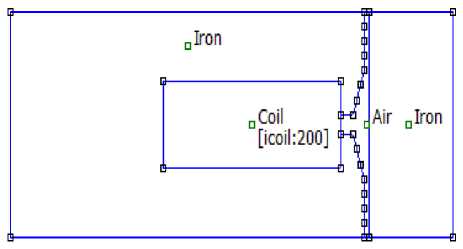
Рис. 2. Расчет магнитной цепи прямоугольной формы в FEMM при p = 3, I = 5 А, W = 200, J = 2,19 А/мм²: а – расчетная схема; б – результат расчета

Fig. 2. Calculation of a rectangular magnetic circuit in FEMM at p = 3, I = 5 А, W = 200, J = 2,19 А/mm²: a – calculation scheme; б – calculation result

б

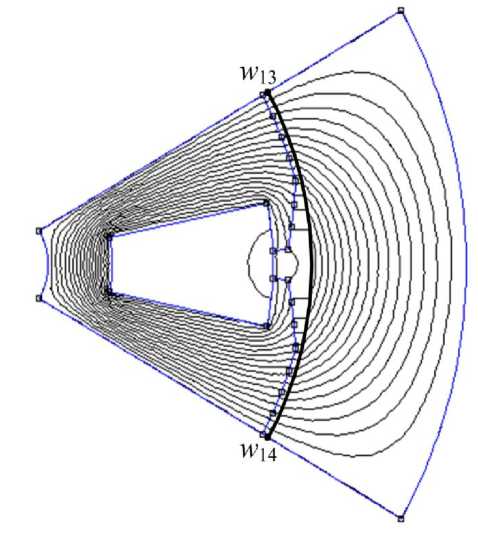
На рис. 3, а представлена расчетная схема сектора магнитной цепи синхронной машины на пару полюсов в FEMM, на рис. 3, б – результат расчета этой магнитной цепи при p = 3, I = 5 А, W = 200, J = 3 А/мм².

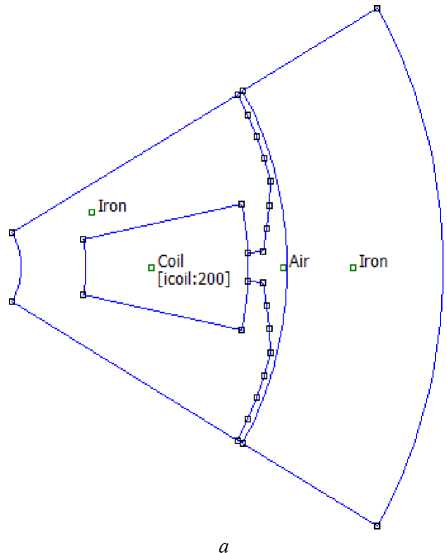
Рис. 3. Расчет магнитной цепи синхронной машины на пару полюсов в FEMM при p = 3, I = 5 А, W = 200, J = 3 А/мм²: а – расчетная схема; б – результат расчета

Fig. 3. Calculation of a synchronous machine magnetic circuit for a pair of poles in FEMM at p = 3, I = 5 А, W = 200, J = 3 A/mm²: a – calculation scheme; б – calculation result

б

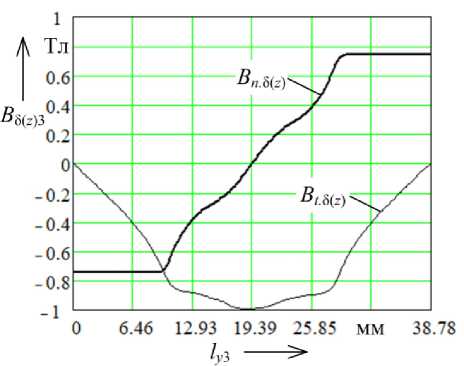
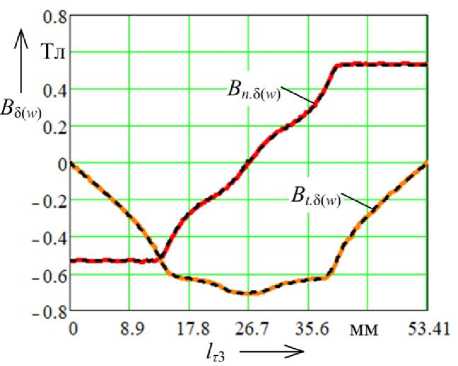
На рис. 4, а изображены кривые нормальной и тангенциальной составляющих магнитной индукции вдоль линии z ₁₃ – z ₁₄ (рис. 2, б ), рассчитанные в программе FEMM. На рис. 4, б показаны кривые нормальной и тангенциальной составляющих магнитной индукции вдоль дуги окружности w 13 – w 14 (рис. 3, б ), рассчитанные в программе FEMM (сплошные линии), а также с использованием рассмотренной методики по формулам (12), (13) и (9) (пунктирные линии).

а                                                   б

Рис. 4. Нормальная и тангенциальная составляющие магнитной индукции в воздушном зазоре синхронной машины на пару полюсов при p = 3: а – магнитная цепь прямоугольной формы; б – сектор магнитной цепи Fig. 4. The normal and tangential components of magnetic induction in the air gap of a synchronous machine per pair of poles at p = 3: a – rectangular magnetic circuit; б – magnetic circuit sector

При сравнении расчетных значений для кривых нормальной и тангенциальной составляющих, рассчитанных с использованием методики и в FEMM, наибольшая относительная погрешность для p = 3 получена для кривой тангенциальной составляющей магнитной индукции (0,25 %).

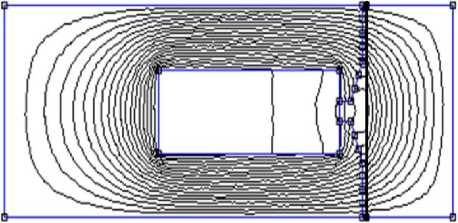
На рис. 5, а приведена расчетная схема магнитной цепи прямоугольной формы в FEMM, на рис. 5, б – результат расчета этой магнитной цепи при p = 4, I = 5 А, W = 200, J = 2,92 А/мм².

^14

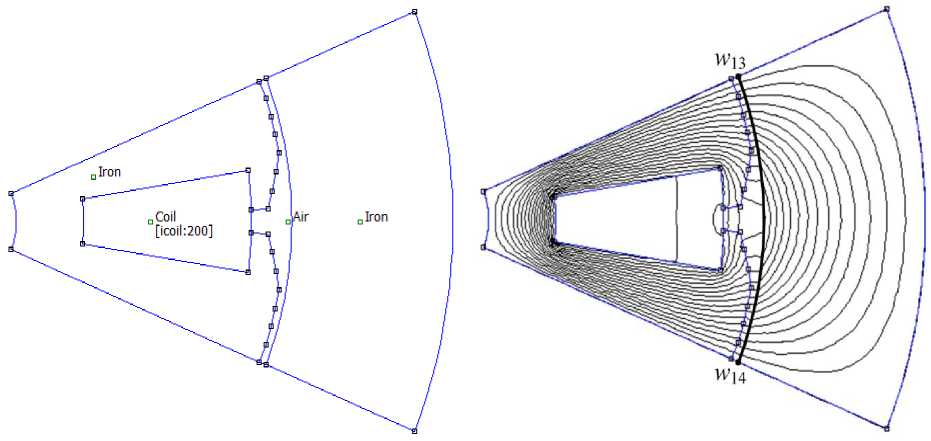
На рис. 6, а представлена расчетная схема сектора магнитной цепи синхронной машины на пару полюсов в FEMM, на рис. 6, б – результат расчета этой магнитной цепи при p = 4, I = 5 А, W = 200, J = 4 А/мм².

а                                                б

Рис. 6. Расчет магнитной цепи синхронной машины на пару полюсов в FEMM при p = 4, I = 5 А, W = 200, J = 4 А/мм²: а – расчетная схема; б – результат расчета

Fig. 6. Calculation of a synchronous machine magnetic circuit for a pair of poles in FEMM at p = 4, I = 5 А, W = 200, J = 4 A/mm²: a – calculation scheme; б – calculation result

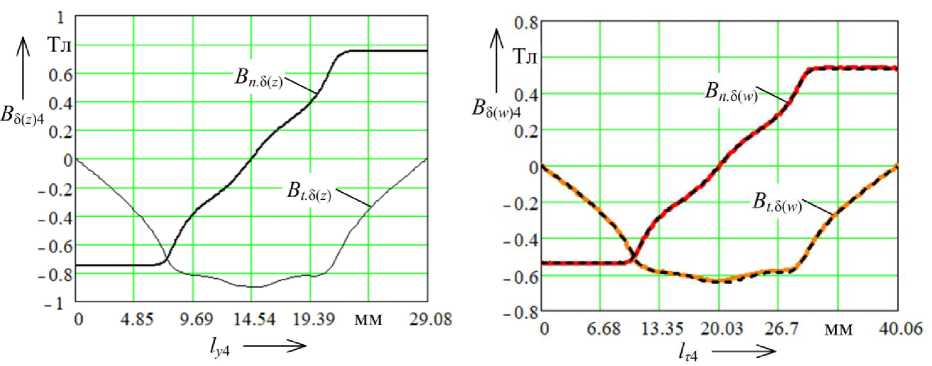
На рис. 7, а представлены кривые составляющих магнитной индукции вдоль линии z 13 – z 14 (рис. 5, б ), вычисленные в программе FEMM. На рис. 7, б – кривые нормальной и тангенциальной составляющих индукции вдоль дуги окружности w 13 – w 14 (рис. 6, б ), рассчитанные в программе FEMM (сплошные линии) и с использованием методики (пунктирные линии).

а

б

Рис. 7. Нормальная и тангенциальная составляющие магнитной индукции в воздушном зазоре синхронной машины на пару полюсов при p = 4: а – магнитная цепь прямоугольной формы; б – сектор магнитной цепи Fig. 7. The normal and tangential components of magnetic induction in the air gap of a synchronous machine per pair of poles at p = 4: a – rectangular magnetic circuit; б – magnetic circuit sector

Наибольшая относительная погрешность для p = 4 получена для кривой тангенциальной составляющей магнитной индукции (0,47 %).

Как можно видеть на рис. 4 и 7, величина магнитной индукции вдоль рассмотренных линий, соответствующих внутренней поверхности сердечника статора, для магнитных цепей на комплексных плоскостях Z и W изменяется по одинаковому закону, который зависит от заданной формы полюсных наконечников. Значения модулей нормальной и тангенциальной составляющих индукции магнитной цепи на плоскости W (рис. 4, б и 7, б ) в соответствии с расчетными выражениями (12), (13) и (9) меньше этих же величин магнитной цепи на плоскости Z (рис. 4, а и 7, а ) в a^xln ( a ) раз. Для рассмотренного примера в 1,027375 ^145,6ln (1,027375) = 1,377 раза.

Заключение

В результате проведенных исследований:

• 1)    предложена методика расчета магнитной цепи синхронной явнополюсной машины, которая основана на двух методах – методе конечных элементов и методе конформных отображений. Для расчета магнитной цепи машины на пару полюсов достаточно решить полевую задачу для более простой магнитной цепи прямоугольной формы и далее рассчитать напряженность и индукцию магнитного поля сектора магнитной цепи синхронной машины с заданным числом пар полюсов;

• 2)    в качестве примера применения рассмотренной методики выполнен расчет магнитного поля для шестиполюсной и восьмиполюсной синхронных машин с одинаковыми размерами элементов магнитной цепи, магнитной проницаемостью стали, МДС обмотки возбуждения на полюс и с учетом неравномерного воздушного зазора между полюсным наконечником и сердечником статора;

• 3)    для проверки результатов расчетов магнитное поле сектора магнитной цепи машины рассчитано также методом конечных элементов в пакете программ FEMM. Выполнено сравнение кривых нормальных (тангенциальных) составляющих магнитной индукции в воздушном зазоре, рассчитанных по предложенной методике и с использованием FEMM. Наибольшая относительная погрешность для p = 3 получена для кривой тангенциальной составляющей магнитной индукции (0,25 %), для p = 4 – для кривой тангенциальной составляющей магнитной индукции (0,47 %);

• 4)    предложенная методика может быть полезна при оптимизации магнитной цепи явнополюсной синхронной машины, определении оптимальной формы полюсных наконечников с целью обеспечения синусоидальной формы распределения магнитной индукции в воздушном зазоре.