Методика расчета механики систем связанных тонких упругих стержней по дифференциальной модели
Автор: Красноруцкий Д.А.
Статья в выпуске: 2, 2016 года.
Бесплатный доступ
Предложена методика расчета геометрически нелинейного динамического деформирования системы связанных между собой стержней по дифференциальной модели тонкого упругого стержня. Деформирование каждого стержня описывается 12 дифференциальными уравнениями с краевыми условиями. Краевые условия для каждого стержня формируются из условий закрепления, нагружения и условий стыковки стержней между собой. Полученная нелинейная краевая задача решается численно, для этого требуется многократно решать большие СЛАУ, матрицей которых является матрица Якоби совокупности дифференциальных уравнений, краевых условий и условий стыковки для всех стержней, входящих в систему. На главной диагонали такой матрицы стоят блоки от дифференциальных уравнений и краевых условий для каждого отдельного стержня, и эти блоки связаны между собой в остальной части матрицы элементами, полученными из уравнений связи между стержнями в системе. В статье предлагается метод решения таких блочных разреженных СЛАУ, на главной диагонали которых стоят невырожденные блоки, связанные с другими блоками относительно небольшим количеством уравнений. Решение исходной СЛАУ распадается на решение нескольких систем меньшего размера (для каждого блока) и решения СЛАУ размером, равным числу ненулевых строк, связывающих матричные блоки. Поэтому предлагаемый метод эффективен при относительно небольшом по сравнению с размерами матрицы количестве ненулевых строк, связывающих выделенные матричные блоки, стоящие на главной диагонали. В статье приведены тестовые примеры расчета больших перемещений нагруженных рам, результаты расчета по предложенной методике сравниваются с результатами расчета в конечно-элементном пакете ANSYS. Результаты расчетов по методам практически совпали, точность совпадения зависит от дискретизации моделей.
Система связанных стержней, стержневая система, рама, ферма, вантовая конструкция, дифференциальная модель стержня, нелинейная динамика, большие перемещения, метод решения слау, разреженная матрица
Короткий адрес: https://sciup.org/146211615
IDR: 146211615 | УДК: 539.3 | DOI: 10.15593/perm.mech/2016.2.06
Текст научной статьи Методика расчета механики систем связанных тонких упругих стержней по дифференциальной модели
PNRPU MECHANICS BULLETIN
Расчету механики стержневых систем, под которыми обычно понимают систему шарнирно или жестко соединенных между собой в узлах стержней (ферменные и рамные конструкции), посвящено очень много научных трудов [1–10]. Под системой связанных между собой стержней будем понимать более широкий класс конструкций, чем просто рамы и фермы. Это могут быть вантовые конструкции, буксируемые системы, висячие тросовые конструкции, гибкие трубопроводы, системы валов, провода участка цепи линии электропередачи, сети, и даже лопасти винта вертолета можно представить как стержни с определенным аэродинамическим профилем.
Обычно для расчета стержневых систем используется метод конечных элементов [1, 2, 4–6, 11–12]. Широкое распространение конечно-элементного подхода можно объяснить универсальностью его применения для стержневых систем с произвольной геометрией. В ряде публикаций подвергается сомнению корректность получаемых в коммерческих конечно-элементных пакетах (таких как NASTRAN, ANSYS, Cosmos, Lira) результатов расчета геометрически нелинейного деформирования стержневых систем [1]. Эти сомнения связаны прежде всего со слабой проработкой создателями этих программных продуктов вопросов устойчивости и бифуркации форм равновесия при геометрически нелинейном деформировании. При одной и той же нагрузке могут существовать несколько равновесных конфигураций, достижение которых зависит от способа приложения этой нагрузки и предыстории деформирования. В [1] отмечается необходимость при рассмотрении задач о больших перемещениях стержневых систем учитывать инерцию и предла- гается динамический подход к расчету стержневых систем методом конечных элементов, при этом рассматриваются стержневые системы с узловым расположением масс и нагрузок. В [2] развивается геометрически нелинейная теория деформирования стержневых систем с анализом бифуркаций форм равновесия в конечно-элементной формулировке. В работах [11–12] метод конечных элементов используется для анализа нелинейного деформирования и устойчивости пространственных стержней с учетом поперечного сдвига при больших упругих перемещениях. В работе [3] рассчитывают критическую силу Г-образной рамы с помощью дифференциальных уравнений стержней и сравнивают с решением в NASTRAN.
Другой аспект, в котором традиционный конечно-элементный подход можно усовершенствовать, – это скорость сходимости итерационного процесса при расчете нелинейных конфигураций. Так, в [2] предлагается метод, позволяющий сохранить в уравнениях метода конечных элементов все нелинейные члены, что, как утверждает автор, ускоряет сходимость итерационной процедуры решения.
В представленной статье предлагается методика расчета нелинейного деформирования системы связанных между собой тонких упругих стержней произвольной формы по дифференциальной модели стержня [13, 14]. Эта модель позволяет включать в расчетную схему распределенные и сосредоточенные нагрузки любой природы. Это могут быть силы веса, инерционные силы (в том числе возникающие при несовпадении центра масс и центра жесткости поперечного сечения), аэродинамические силы, силы от протекающего потока жидкости по шлангу, внутреннее и внешнее демпфирование (точечные демпферы), силы от контактного взаимодействия, электромагнитные силы, температурные деформации и т.д. Кроме того, в расчетную схему можно внести произвольную зависимость любых параметров нагружения и характеристик поперечных сечений от любых других параметров деформирования (перемещений, углов поворота, скоростей, деформаций, времени, текущих координат и т.д.), следовательно, можно задавать следящие нагрузки, а также реактивные силы и моменты.
Используемая дифференциальная модель криволинейного стержня [13, 14] имеет преимущество перед другими известными дифференциальными моделями [15–18] в том, что в уравнения не входит начальная кривизна осевой линии стержня, что позволяет напрямую описывать стержни с изломами осевой линии и со скачками кривизны. На основе работ [19, 20] в работе [14] разработан алгоритм численного решения нелинейной краевой задачи динамического деформирования тонкого стержня. Преимуществом подхода к решению краевой задачи является назначаемая точность вычисления неизвестных функций из решения нелинейной краевой задачи, которая достигается благодаря методу отложенной коррекции, и специальная учитывающая структуру матрицы Якоби «быстрая» процедура факторизации и решения соответствующих систем линейных уравнений, возникающих в итерационном процессе Ньютона [19, 20, 14]. При составлении системы из стержней в матрице Якоби нарушается блочная трехдиагональная структура из-за условий сочленения стержней между собой. В данной статье предлагается метод решения СЛАУ, позволяющий использовать хорошо зарекомендовавший себя подход [19, 20, 14] для факторизации матриц каждого стержня отдельно и получать решение совместной СЛАУ. В качестве примера приведен пример расчета системы четырех стержней, результаты сравниваются с результатами, полученными в конечноэлементном пакете ANSYS.
1. Дифференциальная модель тонкого стержня
Точки недеформированной осевой линии стержня задаются радиусом-вектором — ( ^ ) = xk ( § ) • i k , где § - параметр, связанный с естественной координатой - длиной стержня s ; i 123 - орты глобальной (неподвижной) системы координат; x 123 ( § ) - координаты точек осевой линии. Здесь и далее по повторяющимся индексам ведется суммирование от 1 до 3.
Для описания ориентации поперечных сечений стержня до деформирования используется «матрица поворота» (матрица начальной геометрии) в ( § ) . Направляющие векторы главных осей инерции поперечных сечений недеформированного стержня имеют вид — j ( § ) = в jk ( § ) • i k ; e 3 - направлен по касательной к осевой линии стержня, здесь и далее неуказанные индексы принимают значения от 1 до 3. Направляющие векторы главных осей поперечного сечения после деформации выражены через компоненты матрицы на-
——
——
чальной геометрии в и матрицы поворота при деформировании X : е . = в jk i k = в jk X kn i n •
Жесткостные характеристики стержня задаются следующими величинами: EJ 1 2 ( § ) -изгибные жесткости; GJ 3 ( § ) - жесткость на кручение; EF ( § ) - жесткость на растяжение-сжатие. Жесткости также могут зависеть от текущей деформированной конфигурации – текущей кривизны осевой линии или удлинения. Инерционные характеристики стержня: р F ( § ) - погонная плотность; р J 123( § ) - произведение плотности и моментов инерции поперечных сечений. Если ось жесткости стержня не проходит через центры инерции поперечных сечений, то задаются координаты центра тяжести поперечного сечения относительно центра жесткости А 12 ( § ) . Вектор положения центров масс относительно центров жесткости R = А1 — * + А2 — * = R n — , , R n = (А1в1 k + А2в2 k )X kn .
На стержень могут действовать внешние распределенные нагрузки и моменты. В общем случае они могут зависеть не только от текущей точки на осевой линии, но и от времени t , пространственного положения, текущей кривизны и других параметров:
q = q ( §, t , U , х ,... ) ,
m = m(§,t,U,X,...). Кроме распределенных силовых факторов на стержень могут действовать сосредоточенные силы и моменты. На концах стержня они задаются через краевые условия. Если сосредоточенные силы и моменты действуют внутри стержня, то они включаются специальным образом в нелинейные уравнения (после применения метода конечных разностей), при этом сохраняется блочный трехдиагональный вид матрицы Якоби, а её размерность увеличивается на 12 с каждой новой точкой приложения сосредоточенных сил или моментов. Такое включение сосредоточенного фактора равносильно разбиению стержня на два стержня, сочлененных в точке его приложения.
Мгновенные угловые ускорения и скорости поворота поперечного сечения стержня относительно главных осей e 1 * ,2,3 имеют следующий вид:
—*—*
Q. = —X X, B?t — X X, B?t = = — X X, B?t
1 mn 3 m kn 2 k mn 3 m kn 2 k , 132 mn 3 m kn 2 k ,
—*—*
Q, = X Вт X, +Х Bt X, Bit, £^9 = е^е, = X Bt Х> Bit, 2 mn 3 m kn 1 k mn 3 m kn 1 k , 231 mn 3 m kn 1 k ,
• ■ ■ ее
^ = X mn 0 1 m X kn Р 2 k + X mn 0 1 m X kn в 2 k ,
^ = ^2 =X mn в ! m X .n в 2 k ,
где точка обозначает производную по времени t .
Система уравнений движения тонкого упругого стержня, описывающая любые повороты поперечных сечений при динамическом деформировании, имеет вид [14]
Ui ,5 = ( 1 + £ ) x j X ji - xi A ;
X kis = ( X„Arn p Л-X„A4 , 5) , C =
Ato , je, m C „₽, „ X „M n ,
EJ , 1
0 0 ]
EJ 2 - 1 0
0 GJ - 1
Q a = p F ( 5 ) ( U i + R ) s ,5 - q i ( 5,~ ) s ,5 ( 1+e ) ;
M, 5 = P J ( 5 ) ^ n в nk X +p F ( 5 ) [ ( j ) p + R p ) R r - ( i j r + R r ) R p ] s , 5 +
+ (- m i ( ^’... ) s , 5 + Xj , 5 X jrQp — Xj , 5 X jpQr )( 1 + s) ,
£ = x j ,5 X jk Q k [ EF ( 5 ) • s ,5 ] 1 + aA T , s ,5 = ( X k ,5 x k ,5 ) 1/2
i = 1,2,3,
< p = 2,3,1, r = 3,1,2,
где a - коэффициент температурного удлинения; A T - изменение температуры; нижний индекс 5 после запятой означает производную по этой переменной.
Система (1) состоит из 18 нелинейных дифференциальных уравнений первого порядка по 5 и второго порядка по времени t . Разрешающими функциями системы (1) являются 18 функций: U 123 ( 5, t ) - проекции вектора перемещений точек осевой линии стержня на оси глобальной системы координат; X j ( 5, t ) - компоненты матрицы, описывающей поворот главных осей инерции поперечных сечений при деформировании; Q 123 ( 5, t ) -глобальные проекции вектора внутренних усилий; M 123 ( 5, t ) - глобальные проекции внутренних моментов.
На девять компонентов матрицы поворота X ( 5, t ) накладываются дополнительные зависимости, которые вытекают из общих свойств матриц поворота. Поэтому на практике [14] вместо компонент используются только 3 функции в качестве параметров поворота, что уменьшает число неизвестных функций и число уравнений с 18 до 12. В качестве параметров поворота выступает о = to j i j - вектор конечного поворота:
Xu= 1 -
1 - cos to/ 2 2\ . sin to 1 - cos to
2 (toj+tok ) , Xi =-—Г tok + 2
to to to
. sin to 1 - cos to n^-----2-----2"
Xik =-------toj +------2----toitok , to - to = A/to1 + to2 + to3 , < to to
to i toj,
i = 1,2,3, j = 2,3,1, k = 3,1,2.
Таким образом, имеем 12 дифференциальных уравнений и 12 неизвестных функций U 1,2,3 , to 1,2,3 , Q 1,2,3 , M 1,2,3 .
2. Нелинейная краевая задача для системы стержней
Нелинейная краевая задача для системы (1) решается численно [14]. Значения разрешающих функций разыскиваются в дискретных точках по длине стержня, производные функций заменяются конечными разностями, уравнения (1) удовлетворяются в точ- ках посередине между узловыми значениями. Погрешность определения разрешающих функций при такой аппроксимации и метод снижения этой погрешности до желаемого уровня приведены в [14]. Затем полученная система нелинейных уравнений решается по методу Ньютона. На каждой итерации матрица СЛАУ (матрица Якоби системы не- линейных уравнений)
имеет блочную структуру [14,
19] и факторизуется следующим образом:
Г I в 2 0
l 6 1
0 I β 3
• .• 0 δ 2
|
A = |
Г A B 2 0 ... |
C 1 A 2 B 3 ... |
0 ... C 2 ... А з ... ... ... |
0 0 0 ... |
0 > 0 0 ... |
= |
||
|
0 |
0 |
0 |
... |
A N |
C N |
|||
|
l D |
0 |
0 |
... |
B N +1 |
А N +1 J |
|||
|
0 ... |
0 |
0 " |
Г а1 |
C 1 |
0 |
... 0 |
||
|
0 ... |
0 |
0 |
0 |
α2 |
с 2 |
... 0 |
||
|
I ... |
0 |
0 |
0 |
0 |
α3 |
... 0 |
||
|
• •• • .• 0 ... |
... I |
... 0 |
... 0 |
... 0 |
... 0 |
... ... .•. а n |
||
|
6 3 ... |
( в |
N +1 + 6 |
N ) |
I J |
l 0 |
0 |
0 |
... 0 |
0 "
• «V
C N a N +1 J
где A – матрица Якоби (матрица, составленная из частных производных системы функций, полученной при применении численной методики [19] к решению нелинейной краевой задачи); Ai , αi – матрицы размером 12×12, матрицы Bi , Ci , βi , D , δi имеют размер 6×12; N – число разбиений стержня при применении численного алгоритма [14] для решения нелинейной краевой задачи; (N +1) - количество узлов; I - единичная матрица 12х12.
Таким образом, имеется эффективный способ [14, 19, 20] решения СЛАУ двухточечной нелинейной краевой задачи для одного стержня, но он не подходит для решения задачи для системы связанных между собой стержней. В этом случае блочная матрица (2) для каждого стержня сама будет являться блоком, стоящим на главной диагонали еще большей матрицы СЛАУ. Для системы n стержней матрица Якоби будет иметь следую- щую структуру:
^^
A =
(д А
А11 A 12
A 21
A 22
A n,1 A n,2
...
1,n
А ... 2,n
...
An,n >
к =1
Решение СЛАУ с матрицей (3) можно получить, например, вычислив обратную матрицу. В силу того что размерность матриц (2) и (3) существенно больше (в среднем от одного до 3 порядков) размерности своих блоков A i , B i , C i , нахождение обратной матрицы невыгодно с вычислительной точки зрения и с точки зрения экономии памяти. Здесь можно поступить так же, как и в случае одного стержня – провести LU-разложение матрицы (3), как в (2), и учесть особенности строения этой матрицы. Такое LU-разложение матрицы (3) требует, помимо хранения матриц Якоби (2), дополнительных массивов памяти для каждого стержня, что увеличивает требуемый объем памяти пропорционально количеству стержней.
На рис. 1 представлена структура матрицы Якоби (3) и её LU-разложения для системы 4 стержней. Элементарный блок – матрица 6×12, белым цветом указаны нулевые элементы, разными цветами – разные типы матриц-блоков: например, красным цветом слева указаны блоки, полученные из уравнений деформирования стержня, синим и зеленым указаны блоки краевых условий или условий стыковки между стержнями.
В данной статье предлагается модифицированный алгоритм решения СЛАУ с матрицей (3), который требует значительно меньше памяти, чем при прямом обращении или факторизации матрицы СЛАУ и факторизации с учетом структуры блоков (см. рис. 1). В задаче о деформировании системы стержней внедиагональные блоки A ij формируются
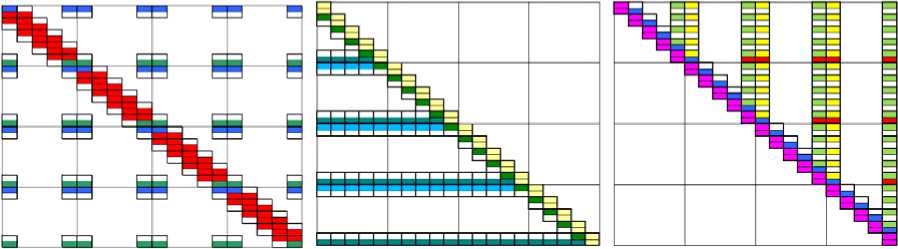
Рис. 1. Структура матрицы Якоби и её LU-факторизации для системы 4 стержней из условий связи между стержнями. Каждый стержень может иметь только 12 краевых условий (в том числе и связей с другими стержнями) по 6 на каждом конце. Поэтому число ненулевых строк у внедиагональных блоков ограничено 12 на каждый стержень и, следовательно, чем больше разбиений, тем меньше относительный объем памяти, требуемый для хранения Aij . Согласно предлагаемому ниже методу отношение объема памяти для решения СЛАУ к объему памяти для хранения исходной разреженной матрицы имеет обратную пропорциональность числу разбиений каждого стержня и прямую пропорциональность количеству стержней в системе.
Предлагаемый ниже метод решения СЛАУ с матрицей (3) может использовать хорошо отработанный аппарат [14, 19, 20] решения СЛАУ с матрицей (2), при этом каждый блок в (3) связан с каким-либо другим несколькими уравнениями, число которых значительно меньше, чем общее число уравнений.
Для такого алгоритма решения СЛАУ отношение объемов, требуемых для хранения внедиагональных блоков и блоков на главной диагонали (матриц Якоби для каждого стержня), зависит от количества стержней в системе и не зависит от дискретизации (количества узловых точек, в которых разыскиваются неизвестные функции) каждого стержня.
3. Метод решения СЛАУ
Пусть имеется система линейных алгебраических уравнений
Ax = b,(4)
где A - квадратная матрица размерностью N х N , | A| * 0 .
Исходную матрицу СЛАУ (4) представим в виде суммы двух матриц:
A = D + C,(5)
где D - блочно-диагональная матрица, |D| * 0 , а матрица С содержит n ненулевых строк ( n < N ), которые описывают связи между блоками на диагонали матрицы A .
Тогда из СЛАУ (4) получим
-
(D + C) x = b ; x = [(E + CD-1) D]"1 b; Dx = (E + CD-1 )"1 b = b,
где E - единичная матрица размером N х N .
Решение СЛАУ (6) эквивалентно решению СЛАУ (4). Из выражения (6) можно заметить, что если все элементы матрицы C равны нулю, тогда b = b и система (6) превращается в (4). В другом случае необходимо вычислить b по формуле (6). При этом необ- ходимо обратить или факторизовать матрицу (E + CD 1) , которая по размеру идентична исходной матрице A (N х N ). Из выражения (6) неочевидно, что для вычисления b вместо (E + CD-1) можно обращать матрицу меньшего размера, а именно размера ( n х n ), где n – количество ненулевых строк в матрице C . Чтобы это стало более очевидным, представим b в следующем виде:
b = b + A b , (7)
тогда из (6) с учетом (7) получим
A b = ( E + CD - 1 ) -1 b - b ;
A b = ( E + CD - 1 )- 1 [ b - ( E + CD - 1 ) b ]; (8)
A b = - ( E + CD - 1 )- 1 CDb .
Выражение (8) определяет слагаемое в (7), которое показывает, как должна измениться правая часть СЛАУ, чтобы осуществить переход от исходной системы (4) к системе (6). Размер вектора-столбца A b совпадает с размером вектора-столбца b , однако можно заметить, что в выражении (8) есть произведение матрицы C на вектор-столбец D - 1 b . Если в матрице C есть нулевые строки, то соответствующие элементы A b будут всегда равны нулю вне зависимости от значений элементов вектора столбца D - 1 b или матрицы ( E + CD - 1 ) . Этот факт дает основание рассматривать вместо (8) следующее выражение, которое позволяет рассчитывать ненулевые элементы A b без выполнения «лишних» операций:
Al b = - ( I + CD )- 1 CD - 1 b ,
где I - единичная матрица размером n х n ; матрица C получена из C путем вычеркива-
ˆ
ˆ
ния нулевых строк ( C имеет размерность n х N ); вектор-столбец A b получен вычеркиванием строк из A b , которые в C являются нулевыми, а матрица D получена из D - 1 вычеркиванием столбцов ( D имеет размерность N х n ), номера которых соответствуют номерам нулевых строк в матрице C . Таким образом, вместо матрицы ( E + CD - 1 ) с размерами N х N имеем матрицу ( I + CD ) размерами n х n , где n - число ненулевых строк в матрице C .
Выражение (9) можно получить по-другому. Сгруппируем ненулевые строки (8) и введем обозначения:
CD-1
E + CD-1
, С D - 1 = ( X - 1 Y ) , ( I + C D ) = X ,
1 N - n у
, (E + CD-1 )-1
,
тогда из (8) следует
Ab =
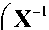
к
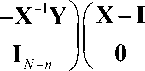
b = -
X 1 ( X - 1 Y ) b
к 0 V
,
откуда получаем искомую формулу (9).
Al b = - X - 1 ( X - 1 Y ) b = - ( I + CD )- 1 CD - 1 b .
На практике при решении краевой задачи для системы стержней имеет смысл не обращать матрицу D , а вычислять её LU-разложение. Чтобы рассчитать вектор-столбец D - 1 b в (9), имея LU-разложение D = LU , нужно решить следующую систему уравнений:
Dz = b , или <
' Ly = b ,
Uz = y ,
где z = D 1 b – искомый вектор-столбец.
Аналогично, чтобы вычислить матрицу ( I + CD ) , нет необходимости вычислять требуемые n столбцов матрицы D - 1, чтобы составить D и перемножать с C , а можно, совершив аналогичное количество операций, решить n раз систему уравнений, подобную (10). Так как имеет место равенство
DT (CD-1)T = CT, уравнения для определения (CD) имеют следующий вид:
U T Y = C T ,
L T Z = Y ,
где Z = ( CD - 1 ) T ,
откуда вычеркиванием строк получим
( CD ) T
После решения (11) можно получить мат-
(
I + CD ) .
Рассмотрим применение (9) к задаче решения СЛАУ с матрицей (3) в методе Ньютона при решении нелинейной краевой задачи о деформировании системы связанных между собой стержней. В выражении (9) производятся следующие вычисления: по имеющемуся LU-разложению матрицы D (имеется разложение для каждого стержня) сначала рассчитывается вектор-столбец x0 = D-1b , затем после вычеркивания строк, которые в C являются нулевыми, вычисляется вектор-столбец b0 = -Cx0. Матрица C как часть матрицы Якоби для системы стержней содержит «связи» между стержнями. Например, пусть три стержня жестко соединены в одной точке, первый стержень сочленяется в i-м узле, второй в j-м узле, а третий в k-м узле. Тогда уравнения связи будут иметь следующий вид:
-
1. Краевые условия первого стержня в точке сочленения i :
-
2. Краевые условия второго стержня в точке сочленения j : равенство перемещений j-k
-
3. Краевые условия третьего стержня в точке сочленения k : уравнения равновесия сил
равенство перемещений i-j
U(') - U j = о , U2^ - U j = о , U3i - U3j = о , равенство поворотов i-j j j) (^i) (j^ (^ (j) j)
CO i CO i 0 , CO 2 0J 2 0 , ^^ 3 CO 3 0 .
U j - U 1(k) — 0, U2j - U2k) — 0, U3j - U3k) — 0, равенство поворотов j-k
) f k)k ) m)j ) m( k ) f j)j ) m( k )
CO i CO i — 0 , CO 2 O 2 — 0 , ^^ 3 CO 3 — 0 .
Qi + Qlj + Qi(k) — 0, Q2i0 + Q2j) + Q2k) — 0, Q3(i) + Q3j + Q^) — 0, моментов
M^i ) + M^ + A/( k ) = 0 A/( i ) + M1^ + A/( k ) = 0 A/( i ) + M1^ + A/( k ) = 0
,,.
Если несколько стержней соединены в одной точке и нет дополнительных ограничений на перемещения этого узла, то краевые условия одного из них должны содержать 3 уравнения равновесия по силам и 3 по моментам. Также допускается, если эти уравнения равновесия будут распределены по нескольким стержням.
Таким образом, имеем по 6 уравнений связи для каждого стержня в точке сочленения. Эти же уравнения, по сути, являются краевыми условиями для каждого отдельного стержня. Дифференцируя уравнения связи по узловым неизвестным, будем получать компоненты матрицы C и некоторые элементы матрицы D .
В общем случае, когда стыковка стержней производится не в глобальных координатах i 1 2 3 , а, например, в подвижных координатах e * — в jk X kn i n , связанных со стержнем, то матрицу C целесообразно строить с помощью численного дифференцирования.
4. Примеры расчета систем стержней
Представленная методика была реализована в программе на языке FORTRAN, рабочее название разрабатываемой программы для расчета нелинейной механики систем стержней – KLPALGSYS. Исходные данные задаются в виде текстовых файлов и имеют определенную универсальную структуру, позволяющую гибко задавать расчетные схемы и управлять процессом расчета; кроме того, эта структура открыта к модернизации. В рамках данной статьи не представляется возможным привести алгоритм работы KLPALGSYS по ряду причин. Во-первых, алгоритм далек от оптимальности и находится на стадии тестирования, отладки и постоянной доработки и развития. Во-вторых, даже его краткое описание займет отдельную статью. Тем не менее ядром этой программы является алгоритм расчета одного стержня KLPALG [14], а основные идеи и принципы описаны выше.
В качестве примера расчета по предлагаемой методике рассмотрим задачу о статическом нелинейном деформировании системы из четырех стержней, жестко соединенных в одной точке 5 под прямыми углами (рис. 2).
1 м
M = 100 Н∙м

1 м
1 м
1 м
Поперечное сечение

5 мм
5 мм
P = 200 Н

X 2
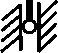
X 1
--------►
O
Рис. 2. Расчетная схема. Плоскость x 1 Ox 2
Длина каждого стержня 1 метр, поперечное сечение – квадрат со стороной 5 мм. Характеристики материала: модуль упругости E = 2,1 - 10пПа, коэффициент Пуассона v = 0,3. В точке 1 стержень жестко защемлен, точка 2 может перемещаться только вдоль оси Ox 1 и свободно поворачиваться, точки 3 и 4 могут свободно перемещаться вдоль оси Ox 2 и также свободно поворачиваться. В точке 5 в направлении оси Ox 3 (из плоскости рис. 2) приложен момент 100 11м и сила 200 Н.
На рис. 3 представлена деформированная конфигурация системы стержней, рассчитанная по предлагаемому алгоритму. Здесь необходимо отметить, что при расчете можно воспользоваться двумя стратегиями: 1) задаём требуемую точность решения краевой задачи, а программа либо достигает её, либо требует увеличить количество разбиений; 2) задаем дискретизацию, а программа достигает максимально возможной точности решения краевой задачи для такого количества разбиений . В данном примере была выбрана вторая стратегия для того, чтобы можно было сравнивать с решением, полученным по методу конечных элементов .
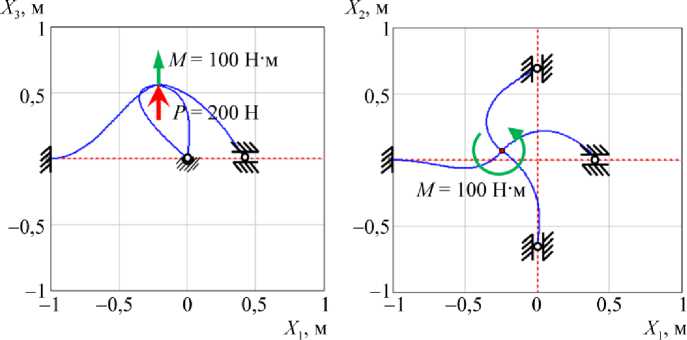
Рис. 3. Деформированная конфигурация. Расчет по предлагаемой методике
Для сравнения была проведена серия расчетов этой системы стержней в геометрически нелинейной постановке в конечно-элементном пакете ANSYS (текст исполняемого файла для одной дискретизации модели представлен ниже), на рис. 4 представлена полученная деформированная конфигурация системы стержней. Количество конечных элементов на один стержень задается переменной nсel . Результаты расчета, в том числе и время расчета, записываются в файлы на жесткий диск путем добавления записей.
С помощью кода, приведенного в тексте программы расчета ANSYS можно сгенерировать и рассчитать раму, состоящую из большего числа стержней, количество клеток задается переменной ncel , при этом значения ncel должны быть четными. Так, при ncel =2 имеем раму из четырех стержней (см. рис. 2). При ncel =4 будет построена рама из 24 стержней, при ncel =6 будет построена рама из 60 стержней, при ncel =8 – рама из 112 стержней, при ncel =10 рама из 180 стержней и т.д. (количество стержней можно рассчитать как 2*( ncel -1)* ncel ). Краевые условия для генерируемых рам соответствуют схеме на рис. 2: слева стержни защемлены, справа подвижные вдоль горизонтального направления шарниры, сверху и снизу подвижные вдоль вертикали шарниры.
Текст программы расчета ANSYS
|
Finish /CLEAR /UNITS, SI /PREP7 ET,1,beam4 MPTEMP,,,,,,,, MPTEMP,1,0 MPDATA,EX,1,,2.1E11 MPDATA,DENS,1,,7850 MPDATA,GXY,1,,2.1E11/(2*(1+0.3)) a=0.005 b=0.005 R,1, a*b, a*(b**3)/12, b*(a**3)/12, a, b, 0 RMORE, ,a*(b**3)/6, , , , hx=1 hy=1 ncel=2 nel=50 bx=(hx*ncel) by=(hy*ncel) ncel2=(ncel*ncel) *do,i,1,ncel-1 k,i*2-1,(hx*i-bx/2),(-by/2) k,i*2,(hx*i-bx/2),(by-by/2) l,i*2-1,i*2 k,i*2-1+ncel2,(-bx/2),(hy*i-by/2) k,i*2+ncel2,(bx-bx/2),(hy*i-by/2) l,i*2-1+ncel2,i*2+ncel2 *enddo lovlap,all lplot LATT, 1, 1, 1 lesize,all,,,nel,, lmesh,all |
ksel,s,loc,x,(-bx/2) dk,all,ux,,,,,uy,uz,rotx,roty,rotz ksel,s,loc,x,(bx/2) dk,all,uy,,,,,uz ksel,s,loc,y,(-by/2) dk,all,ux,,,,,uz ksel,s,loc,y,(by/2) dk,all,ux,,,,,uz allsel FK,KP(0,0,0),FZ,200 FK,KP(0,0,0),MZ,100 /SOLU ANTYPE,STATIC NLGEOM,ON
SOLVE
FINISH /REPLOT /POST1 /SHOW,WIN32C /CONT,1,50 PLNSOL, u,sum, 2
n_num=NODE(0,0,0)
MUU=sqrt(mU(1)*mU(1)+mU(2)*mU(2)+mU(3)*mU(3)) *cfopen,d:\1_output,prn,,APPEND *vwrite,ncel,nel,mU(1), mU(2), mU(3), MUU, (ETime-STime) %i %i %G %G %G %G %G *cfclos |
Ниже будут приведены результаты расчетов рам для ncel =2,4,6,8,10 для разных дискретизаций nel .
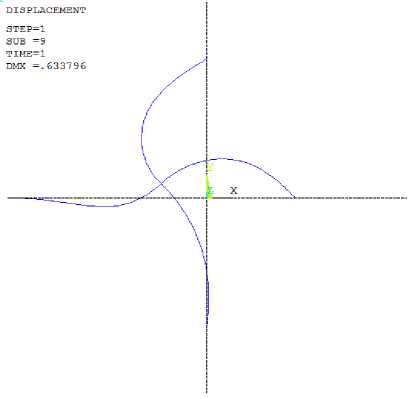
Рис.4. Деформированная конфигурация. Расчет в ANSYS
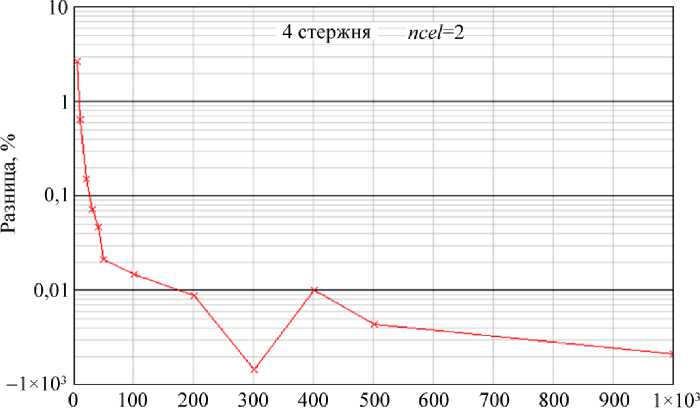
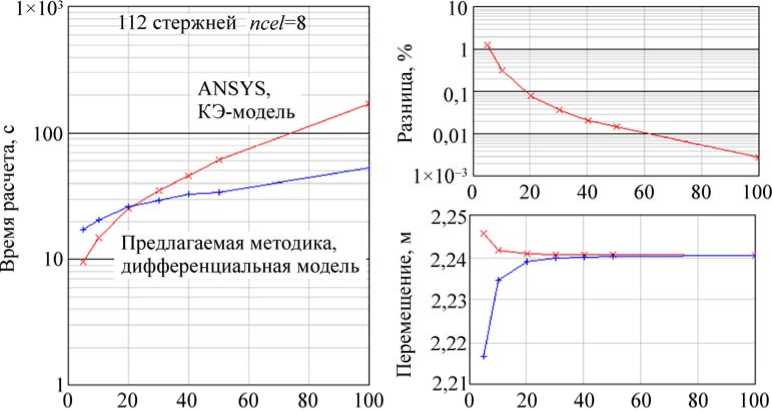
На рис. 5 представлены графики зависимости времени расчета на логарифмической шкале в зависимости от дискретизации моделей для конечно-элементной и дифференциальной модели соответственно. Из рисунка видно, что время расчета КЭ-модели в ANSYS до двух порядков (при увеличении количества КЭ) больше времени расчета по предлагаемой дифференциальной модели. Такое преимущество весьма условно, время расчета существенно зависит от количества стержней в системе. С ростом числа стержней это преимущество уменьшается и КЭ-расчет в ANSYS становится быстрее расчета по дифференциальной модели, далее это будет показано. На рис. 6 представлен график разницы в процентах перемещения точки 5 (центральная точка), рассчитанного в ANSYS и по предлагаемой методике. На рис. 7 представлены графики полных перемещений центральной точки, рассчитанных по МКЭ в ANSYS и по предлагаемой дифференциальной модели.
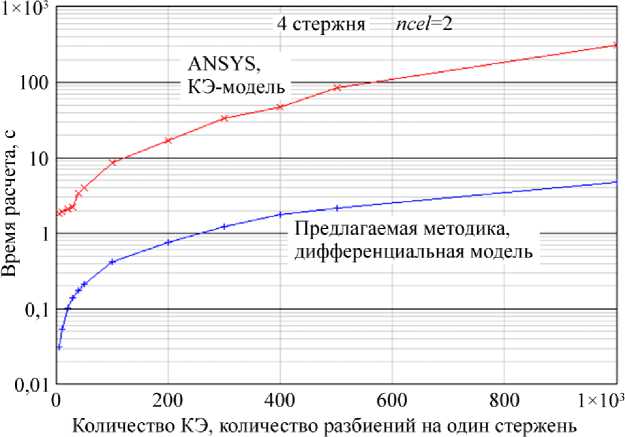
Рис. 5. Время расчета в зависимости от дискретизации моделей (4 стержня, ncel =2)
Количество КЭ, количество разбиений на один стержень
Рис. 6. Разница между рассчитанным максимальным перемещением в ANSYS и по предлагаемому алгоритму (4 стержня, ncel =2)
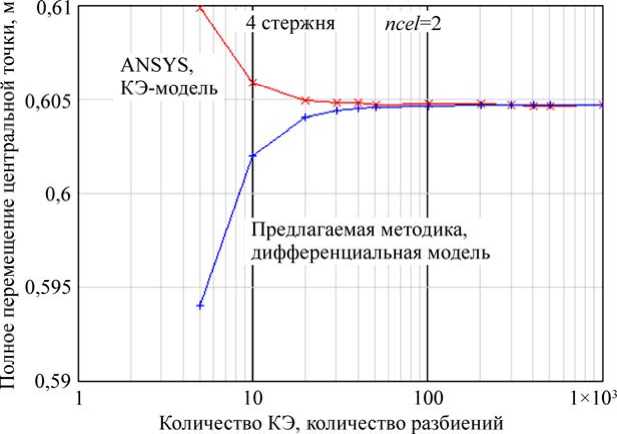
Рис. 7. Полное перемещение центральной точки
Рассмотрим расчеты рам с другим количеством стержней. Были проведены расчеты рам для ncel =4, 6, 8, 10 в ANSYS и KLPALGSYS для разных дискретизаций. На рис. 8 приведен пример деформированной конфигурации для системы 180 стержней, полученный в ANSYS.
На рис. 9–12 приведены результаты расчетов для ncel =4,6,8,10 соответственно. На каждом рисунке представлены три вида зависимостей от величины дискретизации модели: время расчета по двум методам, разница полных перемещений в центральной точке и полные перемещения центральной точки по двум методам. По рис. 9–12 можно проследить, как меняется время расчета по методам с ростом числа стержней в системе. Предлагаемая дифференциальная модель имеет безусловное преимущество в скорости перед КЭ-расчетом в ANSYS примерно до 100 стержней в системе. При 112 и 180 стержнях в системе наблюдается сначала преимущество в скорости ANSYS, но с ростом количества КЭ предлагаемая дифференциальная модель вновь опережает ANSYS.
Рис. 8. Расчет рамы из 180 стержней в ANSYS ( ncel =10)
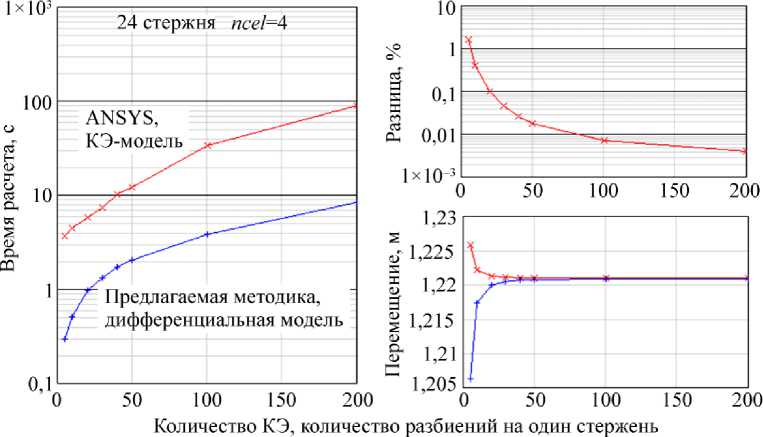
Рис. 9. Результаты расчетов для системы 24 стержней ( ncel = 4)
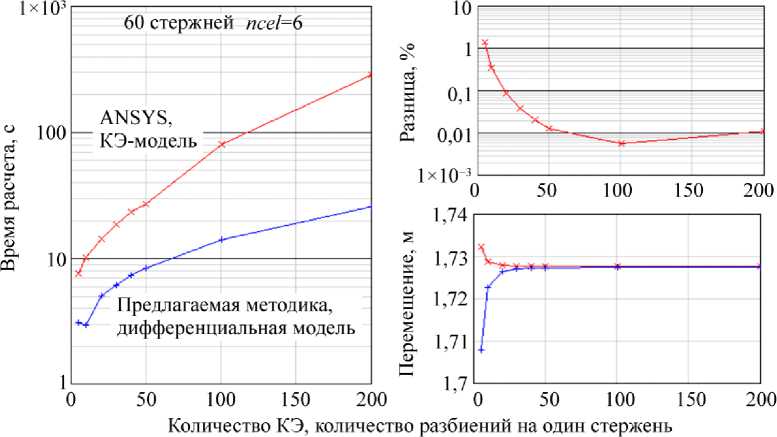
Рис. 10. Результаты расчетов для системы 60 стержней ( ncel =6)
Количество КЭ, количество разбиений на один стержень
Рис. 11. Результаты расчетов для системы 112 стержней ( ncel =8)
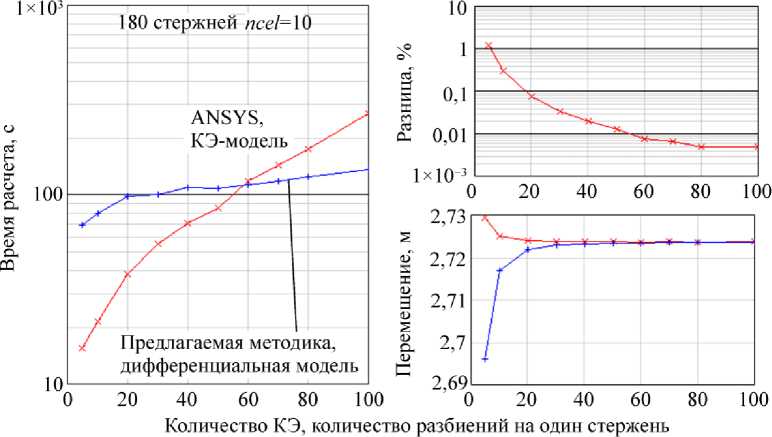
Рис. 12. Результаты расчетов для системы 180 стержней ( ncel =10)
Продолжая анализ полученных результатов, необходимо отметить, что получаемые перемещения по двум методикам сходятся с увеличением дискретизации, причем отчетливо заметно, что для получения приемлемой погрешности определения перемещений требуется до нескольких десятков КЭ на одном стержне в системе. При этом время расчета по предлагаемой дифференциальной модели медленнее растет с увеличением дискретизации, чем при расчете по КЭ-модели ANSYS.
Заключение
В представленной статье описана методика расчета механики систем связанных стержней по дифференциальной модели. Для использования хорошо отработанного аппарата решения нелинейной краевой задачи одного стержня, для случая системы связанных между собой стержней разработан метод решения СЛАУ. Такой подход позволяет получать решение системы с большой матрицей из решения нескольких СЛАУ меньшего размера. Методика расчета реализована в программе на языке FORTRAN, в статье приведены тестовые расчеты нелинейной статики систем стержней. Результаты расчета сравниваются с расчетами методом конечных элементов в пакете ANSYS. Результирующие перемещения двумя методами стремятся друг к другу с ростом дискретизации моделей. По результатам расчетов можно сделать вывод, что предлагаемый дифференциальный подход эффективен и имеет преимущество в скорости расчета перед ANSYS при относительно небольшом количестве стержней в системе (условно до 100 стержней). Это объясняется тем, что при реализации предложенного алгоритма решения СЛАУ из условий стыковки стержней между собой формируется матрица, размер которой растет с увеличением числа стыкуемых стержней, и затраты процессорного времени на решение СЛАУ с этой матрицей быстро растут. Так, например, при расчете стержневой системы из ста стержней в общем случае будем иметь матрицу связей размером 1200×1200 элементов. Затраты на решение СЛАУ с такой матрицей становятся сравнимы с затратами на все остальные вычисления, даже притом, что размер исходной матрицы на порядок, а то и на два превышает размеры матрицы связей. Решение данной проблемы видится в применении других численных методов для решения СЛАУ-связей, либо в ней можно выделить блоки и применить тот же метод решения по блокам. Тем не менее предложенный алгоритм решения хорошо подходит для решения достаточно широкого круга задач механики стержневых систем, в которых не требуется рассчитывать одновременно большое количество стержней.
Список литературы Методика расчета механики систем связанных тонких упругих стержней по дифференциальной модели
- Жиделёв А. В. Динамический подход к расчету геометрически нелинейных стержневых систем: автореф. дис.. канд. техн. наук. -Волгоград, 2003. -23 с.
- Галишникова В. В. Обобщенная геометрически нелинейная теория и численный анализ деформирования и устойчивости пространственных стержневых систем: автореф. дис.. д-ра техн. наук. -Волгоград, 2011. -40 с.
- Raftoyiannis I.G. Nonlinear Stability Analysis of Simple Steel Frames with Load Imperfections//Frontiers of Engineering Mechanics Research. -Feb. 2013. -Vol. 2. -Iss. 1. -P. 15-21.
- Строительная механика. Стержневые системы: учебник для вузов/А.Ф. Смирнов /под ред. А.Ф. Смирнова. -М.: Стройиздат, 1981. -512 с.
- Дарков А.В., Шапошников Н.Н., Строительная механика: учебник для строительных спец. вузов -М., 1986. -607 с.
- Дьяков И.Ф., Чернов С.А., Черный А.Н. Метод конечных элементов в расчетах стержневых систем: учеб. пособие/Ульян. гос. техн. ун-т. -Ульяновск, 2010. -133 с.
- A discrete mechanics approach to Cosserat rod theory. Part 1: Static equilibria/P. Jung, S. Leyendecke, J. Linn, M. Ortiz//Int. J. Numer. Meth. Engng. -2010. -P. 101-130.
- Радченко В.П. Введение в механику деформируемых систем: учеб. пособие. -Самара: Самар. гос. техн. ун-т, 2009. -196 с.
- Petrolito J., Legge K.A. General nonlinear analysis of frames. Proceedings of the 5th Australasian Congress on Applied Mechanics (ACAM 2007). -Brisbane, Australia. 10-12 December, 2007. -Р. 82-88.
- Чернецов Д.А. Процесс нелинейного деформирования стержневых систем без ограничения степени деформации//Изв. Тул. гос. ун-та. Естественные науки. -2012. -Вып. 2. -С. 165-176.
- Levyakov S. V. Formulation of a geometrically nonlinear 3D beam finite element based on kinematic-group approach//Applied Mathematical Modelling. -2015. -Vol. 39. -Iss. 20. -P. 6207-6222.
- Левяков С. В. Нелинейный пространственный изгиб криволинейных стержней с учетом поперечного сдвига//ПМТФ. -2012. -Т. 53, № 2. -С. 128-136.
- Левин В.Е., Пустовой Н.В. Механика деформирования криволинейных стержней: моногр. -Новосибирск: Изд-во Новосиб. гос. техн. ун-та, 2008. -208 с.
- Пустовой Н.В., Левин В.Е., Красноруцкий Д.А. Алгоритм численного решения нелинейной краевой задачи динамического деформирования тонкого стержня//Вестник Пермского национального исследовательского политехнического университета. Механика. -2014. -№ 2. -С. 168-199.
- Жилин П.А. Прикладная механика. Теория тонких упругих стержней: учеб. пособие. -СПб.: Изд-во Политехн. ун-та, 2007. -101 с.
- Светлицкий В.А. Строительная механика машин. Механика стержней: в 2 т. Т. 2. Динамика. -М.: Физматлит, 2009. -383 с.
- Сорокин Ф.Д. Прямое тензорное представление уравнений больших перемещений гибкого стержня с использованием вектора конечного поворота//Изв. РАН. МТТ. -1994. -№ 1. -С. 164-168.
- Nonlinear dynamic deformation simulation for helical rod like objects/H. Du, W. Xiong, H. Wang, Z. Wang, B. Yuan//Engineering Review. -2013. -Vol. 33. -Iss. 3. -P. 233-238.
- Pereyra V. Pasva3: An adaptive finite difference fortran program for first order nonlinear, ordinary boundary problems//Lecture Notes in Computer Science. -1979. -Vol. 76. -P. 67-88.
- Keller H.B. Accurate Difference Method For Nonlinear Two-Point Boundary Value Problems//SIAM J. Numer. Anal. April 1974. -Vol. 11. -No. 2. -P. 305-320.


