Методика расчета нагрузок на трубопровод от динамических воздействий во время полета ракеты-носителя
Автор: Глазков И.Е., Филипов А.Г.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Информатика, вычислительная техника и управление
Статья в выпуске: 6 т.23, 2021 года.
Бесплатный доступ
В данной статье содержатся методические рекомендации по решению задачи динамического нагружения трубопровода [1], необходимых для подачи жидких компонентов в двигатель ракеты-носителя, от динамических воздействий двигательной установки. Даны рекомендации по расчету нагрузок на трубопровод от вибрационных воздействий и гидроудара. Выведено её уравнение движения на составляющие и проведён расчёт нагрузок при гармонических колебаниях ракеты-носителя. В качестве исходных данных для динамического расчёта нагрузок были заданы ускорения узлов крепления двигательной установки и трубопровода, полученные из решения общей динамической задачи для оценки гидродинамической силы для ракеты-носителя. На данном этапе была рассчитана нагрузка на трубопровод с учётом гидроудара массы жидкости для случая начала полета ракеты-носителя, как одного из самых нагруженных для данной системы. При расчёте нагрузок на трубопровод использовался линейный динамический анализ [3]. В результате расчёта были получены усилия в узлах крепления рассматриваемой конструкции, а также усилия, распределённые по длине трубопровода. Описана методика расчёта динамического нагружения трубопровода. Нагрузки на трубопроводы складываются из квазистатических составляющих, в которые обычно включают траекторные перегрузки и низкочастотные динамические составляющие [4] от переходных процессов типа старта, а также дополнительных нагрузок от вибрационных и акустических воздействий. Квазистатические и низкочастотные динамические составляющие в нагрузках [5] обычно имеют достаточно высокую степень определенности и, как правило, оцениваются расчетным путем с использованием соответствующих моделей РКН и навесного оборудования. Получаемые таким образом нагрузки охватывают низкочастотную часть спектра до 20-30 Гц. Для трубопроводов обычно используются балочные модели [6] с упругими опорами и кинематическими связями с днищами баков и двигательной установкой. При расчете силовых факторов в сечениях трубопроводов (продольной и перерезывающих сил, изгибающих и крутящего моментов, усилий в узлах опирания) топливо допускается считать замороженным (без учета скорости движения). Скорость движения жидкости должна учитываться при оценке давления гидроударов в трубопроводах для расчета напряженно-деформированного состояния трубопроводов от внутреннего давления.
Квазистатика, динамическая модель, конечно-элементная модель, перегрузки, переходный процесс, трубопровод, гидроудар, ракета-носитель
Короткий адрес: https://sciup.org/148323604
IDR: 148323604 | УДК: 629.78 | DOI: 10.37313/1990-5378-2021-23-6-78-82
Method of calculation of loads of the pipeline from dynamic influences in the flight time of the launch vehicle
This article considers the solution of the problem of dynamic loading of the pipeline [1], which is necessary to supply fuel to the booster engine. The method of calculating the dynamic loading [2] of the pipeline is described. Its equation of motion is decomposed into components and loads are calculated for harmonic vibrations of the launch vehicle. The accelerations of the propulsion system and pipeline attachment points obtained from solving a general dynamic problem for estimating the hydrodynamic force for a launch vehicle were set as initial data for dynamic load calculation. At this stage, the load on the pipeline was calculated taking into account the hydraulic shock of the liquid mass in the event of the launch vehicle flight, as one of the most loaded for this system. Nonlinear dynamic analysis was used to calculate pipeline loads [3]. As a result of the calculation, the forces in the attachment points of the structure under consideration, as well as the forces distributed along the length of the pipeline, were obtained. The method of calculating the dynamic loading of the pipeline is described. Pipeline loads consist of quasi-static components, which usually include trajectory overloads and low-frequency dynamic components [4] from transient processes such as start-up, as well as additional loads from vibration and acoustic influences. Quasi-static and low-frequency dynamic components in loads [5] usually have a fairly high degree of certainty and, as a rule, are estimated by calculation using appropriate RCN models and attachments. The loads obtained in this way cover the low-frequency part of the spectrum up to 20-30 Hz. Spatial beam models [6] with elastic supports and kinematic connections with tank bottoms and propulsion system are usually used for pipelines. When calculating the force factors in the sections of pipelines (longitudinal and shearing forces, bending and torques, forces in the support nodes), the fuel is allowed to be considered frozen (without taking into account the speed of movement). The fluid velocity should be taken into account when assessing the pressure of hydraulic shocks in pipelines to calculate the stress-strain state of pipelines from internal pressure.
Текст научной статьи Методика расчета нагрузок на трубопровод от динамических воздействий во время полета ракеты-носителя
Данная статья посвящена разработке методики для расчета нагрузок на трубопровод от динамических и акустических воздействий. Дополнительные нагрузки на трубопровод создают виброакустические воздействия. Учитывая, что вибрации в значительной мере создаются акустическими пульсациями внешнего давления, а также пульсациями тяги двигателей, при расчете дополнительных нагрузок на трубопровод достаточно рассмотреть в качестве входных воздействий случайные вибрационные воздействия, задаваемые в виде кинематических возмущений в узлах крепления трубопровода к
днищу бака, двигательной установке и корпусу ракеты-носителя (РН).
Проблема решения задачи динамического нагружения данного типа трубопровода остается открытой. В связи со сложной конструкционной формой трубопровода (сильные изгибы), следует учитывать гидроудар при начале полета РН не только на выходе и на входе трубопровода, но также непосредственно в изгибах.
ОПИСАНИЕ МЕТОДИКИ РАСЧЁТА НАГРУЗОК
Рассматривались различные подходы к анализу гидроударов в трубопроводе с использованием программного комплекса MSC.NASTRAN и анализировались различные варианты физической постановки задач о гидроударе. В первой постановке предполагается, что жидкость в трубе покоится (имеет нулевую скорость), а в каче- стве внешнего воздействия задается быстро нарастающая скорость в крайнем узле (в задвижке) до некоторой постоянной величины. Во второй постановке – жидкость в трубе течет с постоянной скоростью и в крайнем узле закрывается задвижка, то есть скорость с постоянной величины достаточно быстро снижается до нуля.
В данной статье рассмотрим первый вариант задачи, который моделирует случай запуска двигательной установки и отрыв РН от стартового стола. Моделирование и анализ трубопровода произведем с помощью программ Femap и MSC. NASTRAN [13]. Данный подход предполагает моделирование столба жидкости в трубопроводе с помощью балочных элементов с приведенными жесткостными и инерционными характеристиками. Также следует отметить, что рассматривался вариант с абсолютно жесткими стенками, который предполагает только сжатие жидкости.
В результате расчета динамики РН определяются ускорения во всех сечениях связи соответствующего трубопровода с корпусом РН, днищами баков и двигательной установкой. Определенные таким образом временные зависимости ускорений задаются в качестве кинематических воздействий на динамическую модель трубопровода при автономном расчете нагрузок на трубопроводе.
В качестве исходных данных для динамического расчёта нагрузок задаются ускорения узлов крепления и ускорения осцилляторов, моделирующих колебания двигательной установки, полученные из решения общей динамической задачи для оценки динамической силы для РН. Также необходимо задать давление в трубопроводе. Моделирование столба жидкости в трубопроводе происходит с помощью балочных элементов с приведенными жесткостными и инерционными характеристиками. Гидроудар моделировался следующим способом: проведение расчета с нулевыми начальными условиями (жидкость в трубопроводе находится в состоя- нии покоя), а в качестве внешнего воздействия задавалось расчетное давление в местах изгиба с учетом гидроудара, равное 78 МПа, полученное со входа в двигательную установку. При расчете на прочность трубопровода в поперечных направлениях следует учитывать массу компонента жидкости, заполняющего трубопровод. Максимальное значение продольной силы определяется следующим образом:
F = PnR2, где Р – давление.
Зная, что удельный вес жидкости есть произведение ee плотности ρ и ускорения свободного падения g, мы получим:
тж = 0.668VTp ^
где VT - объем трубопровода, рж - плотность жидкости.
Предварительно была построена динамическая конечно-элементная модель топливного бака и РН в целом. Далее необходимо провести расчёты динамического нагружения РН от соответствующих продольных воздействий при различных случаях нагружения РН.
На рисунке 1 показана конечно-элементная модель трубопровода, созданная с помощью линейных (Beam) элементов. Трубопровод проложен от нижнего днища бака до двигательной установки.
Входные воздействия в узлах крепления к корпусу РН, днищам баков и двигателю задаются в виде спектральных плотностей мощности, взаимные спектральные плотности предполагаются равными нулю.
В результате расчетов получаются среднеквадратичные значения ускорений, усилий и моментов в сечении трубопровода, а также среднеквадратичные значения силовых факторов в узлах связи трубопровода с элементами РН.
На данном этапе мы рассчитаем нагрузку на трубопровод с учётом массы жидкости при случае «Старт», (один из самых нагруженных для данной системы). При расчёте нагрузок на трубопровод
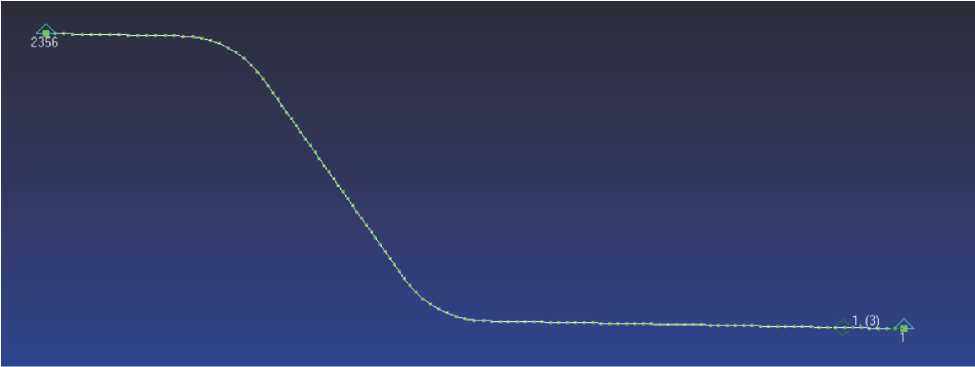
Рисунок 1 – Конечно-элементная модель трубопровода
использовался линейный динамический Transient Dynamic/Time History, в котором в качестве нагружения была приложена сила тяги в тоннах при случае «Старт» (см. рис. 2). Значения полученных перегрузок приведены на рисунке 3, а значения усилий по длине трубопровода на рисунке 4.
На рисунке 3 изображен график результата расчета, где видно, что максимальная пере- грузка на трубопровод равна 5,46g. Полученные результаты приведены вдоль оси X РН, что соответствует «наихудшему» (максимальному) случаю нагружения. Для сравнения на графике также приведены результаты расчета ДУ. В данном случае гидроудар в значительной большей мере реализовался на трубопроводе, чем на двигателе.
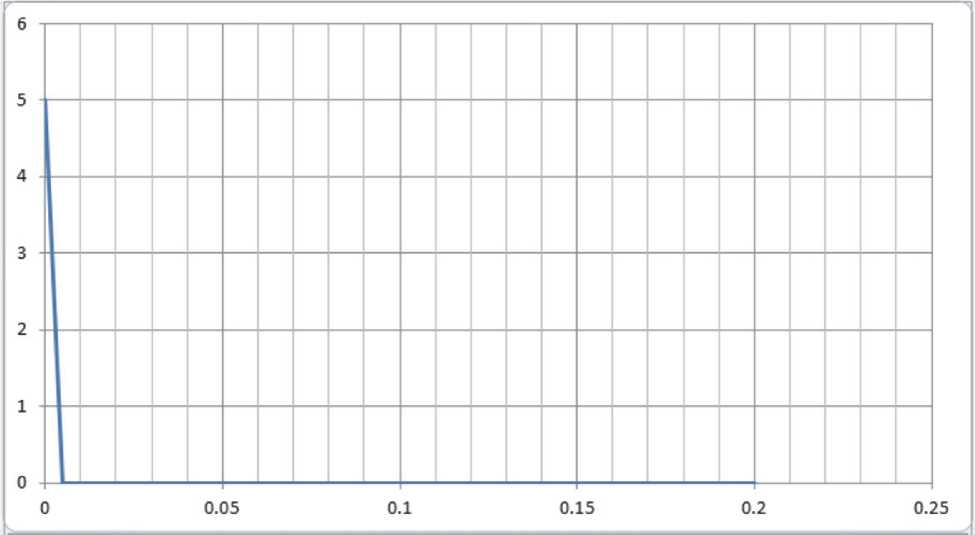
Рисунок 2 –Гидроудар на входе в трубопровод при случае нагружения «Старт»
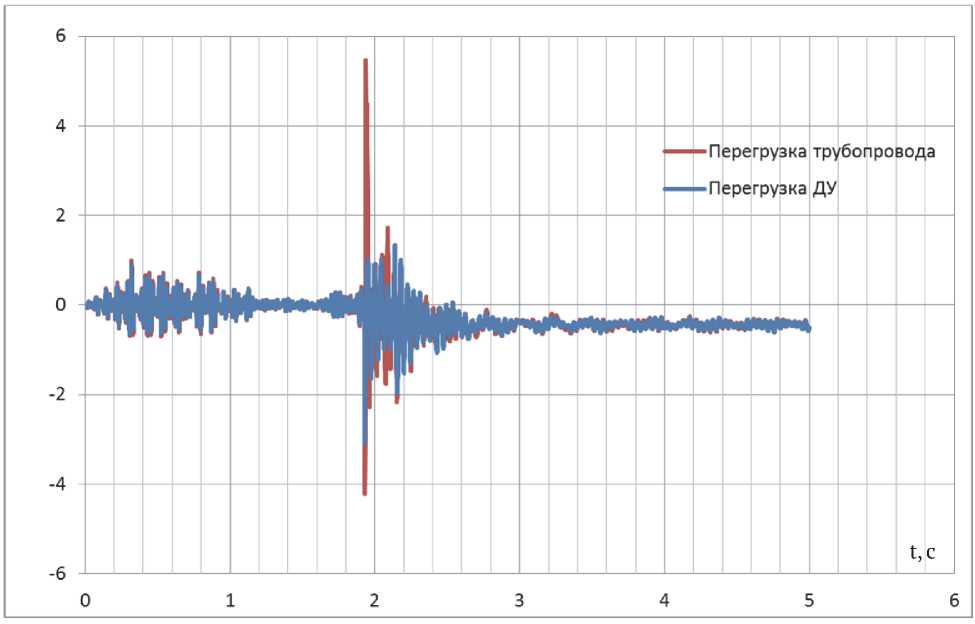
Рисунок 3 –График перегрузок, реализующихся на ДУ и трубопроводе при случае нагружения «Старт»
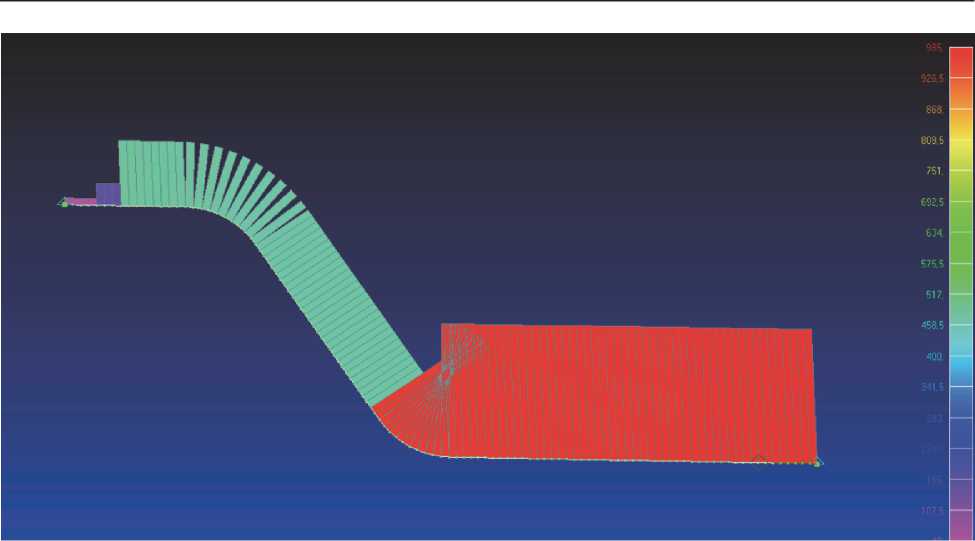
Рисунок 4 – Распределение усилий в элементах по длине трубопровода
На рисунке 4 видно, как происходит распределение усилий по длине трубопровода.
ЗАКЛЮЧЕНИЕ 5.
В статье представлена методика расчета нагрузок на трубопровод от динамических и 6. акустических воздействий. Разработаны методические указания по расчету нагрузок на трубопровод с помощью программ Femap и MSC. Nastran, которые складываются из квазистати- 7.
ческих и динамических составляющих от переходного процесса. Учитывая, что вибрации в значительной мере создаются акустическими 8. пульсациями внешнего давления, а также пульсациями тяги двигателя, при расчете дополнительных нагрузок достаточно рассмотреть в 9. качестве входных воздействий случайные вибрационные воздействия, задаваемые в виде кинематических возмущений в узлах крепления трубопровода к днищу бака и двигателю. 10.
Список литературы Методика расчета нагрузок на трубопровод от динамических воздействий во время полета ракеты-носителя
- Шмаков, В.П. Об уравнениях осесимметричных колебаний цилиндрической оболочки с жидким заполнением / В.П. Шмаков // Известия АН СССР. Механика и машиностроение. - 1964. - № 1. - С. 170 - 173.
- Моисеев Н.Н. К теории колебаний упругих тел, имеющих жидкие полости / Н.Н. Моисеев // Прикладная математика и механика. - 1959. - Т. 23. -№ 5. - С. 862 - 878.
- Александрович, Л.И. Собственные колебания упругого осесимметричного сосуда произвольного контура / Л.И. Александрович, Р.Е. Лампер // Труды VI Всесоюзной конференции по теории оболочек и пластинок, 1966. - М.: Наука, 1966. -С. 25 - 27.
- Лампер, Р.Е. К расчёту собственных колебаний баков методом Ритца с варьируемым параметром / Р.Е. Лампер // Труды VII Всесоюзной конференции по теории оболочек и пластинок, 1969. - М.: Наука, 1970. - С. 351 - 354.
- Шиманский, Ю.А. Динамический расчёт судовых конструкций / Ю.А. Шиманский - Л.: гос. издат. судостроительной промышленности, 1963. - С. 444.
- Прокудин, О.А. Определение динамических характеристик металлополимерного слоистого стержня / О. А. Прокудин, Л. Н. Рабинский, К. Т. Чан // Труды МАИ. - 2021. - № 120. - DOI 10.34759/ trd-2021-120-06.
- Peeters, M. Dynamic testing of nonlinear vibrating structures using nonlinear normal modes / M. Peeters, G. Kerschen, J.C. Golinval // Journal of Sound and Vibration. - 330(2011). - P. 486-509
- Renson, L. Nonlinear modal analysis of the SmallSat spacecraft / L. Renson, G. Kerschen, A. Newerla // Topics in Nonlinear Dynamics. - Belgium.- Vol. 3. - January 2012. - Pp. 45-60. DOI: 10.1007/978-1-4614-2416-1_5.
- Jang, J. Model updating of a full-scale FE model with nonlinear constraint equations and sensitivity-based cluster analysis for updating parameters / Jinwoo Jang, Andrew W. Smyth // Mechanical Systems and Signal Processing. - 83 (2017). - Pp. 337-355.
- Kerschen, G. Past, present and future of nonlinear system identification in structural dynamics / Gaëtan Kerschen, Keith Worden, Alexander Vakakis, JeanClaude Golinval. // Mechanical Systems and Signal Processing. - Elsevier. - 2006. - 20 (3). - Pp.505-592.
- Кудинов, А.Н. Исследование устойчивости автономных нелинейных динамических систем / А.Н. Кудинов, А.Н. Катулев , А.Ю. Кузнецов // Динамические и технологические проблемы механики конструкций и сплошных сред: матер. XVI Меж-дунар. симпоз. им. А.Г. Горшкова. - М.: МАИ, 2010. - Т. 1. - С. 110-112.
- Косачев, И.М. Методология высокоточной нелинейной фильтрации случайных процессов в стохастических динамических системах с фиксированной структурой. Часть 1 / И. М. Косачев, К. Н. Чугай, К. А. Рыбаков // Труды МАИ. - 2019. - № 105. - С. 18.
- Рычков, С.П. Моделирование конструкций в среде Femap with NX Nastran / С.П. Рычков . - М.: ДМК Пресс, 2013. - 784 с.
