Методика расчета одноосевого микро-опто-электро-механического преобразователя угловых скоростей

Направление исследования и разработки датчиков угловых скоростей на основе микро-электро-механических (МЭМ) технологий является перспективным в приборостроении с точки зрения возможности различных применений в системах управления подвижными объектами. За последние несколько лет широкое распространение получили МЭМ-датчики угловых скоростей, выполненные на основе емкостного метода измерения, имеющие ряд достоинств, таких как простота их использования, малые массогабаритные показатели и энергопотребление. Но при разработках емкостных МЭМ-датчиков также встречается ряд ограничений, таких как возможность пробоя конденсаторов и нелинейность функции преобразования, сильно зависящая от глубины модуляции емкостного зазора [1–3].

Для устранения таких недостатков и обеспечения гальванической развязки цепи возбуждения чувствительного элемента (ЧЭ), а также получения квазилинейной функции преобразования предлагается использовать схему одноосевого МОЭМ-преобразователя угловых скоростей на основе ОТЭ, построенного в системе «призма полного внутреннего отражения (ППВО) – воздух – ЧЭ». Такой МОЭМ-преобразователь угловых скоростей обеспечивает рабочие диапазоны значений зазора около сотен нанометров, что на порядок меньше, чем у емкостных МЭМС-гироскопов, и приводит к уменьшению требуемых амплитуд возбуждаемых колебаний в пьезоэлементе. Также за счет применения оптического считывания результатов измерений такие МОЭМ-преобразователи по сравнению с другими аналогами имеют меньшую минимальную детектируемую угловую скорость (~ 10–6 рад/с) и широкий динамический диапазон измерения (~ 67 дБ в частотном диапазоне 20 кГц) [4, 5].

Целью данной работы является обеспечение определения конструктивных параметров МОЭМ-преобразователя угловых скоростей на основе ОТЭ для реализации заданного диапазона функционирования.

Алгоритм расчета одноосевого МОЭМ-преобразователяугловых скоростей на основе ОТЭ

Алгоритм расчета МОЭМ-преобразователя угловых скоростей на ОТЭ основан на обеспечении заданного диапазона измерения с высокой чувствительностью (рис. 1) [6, 7]. Исходными данными при расчете преобразователя являются: диапазон измерения, уровень чувствительности, динамический диапазон, основная и дополнительная погрешности, а также массогабаритные показатели.

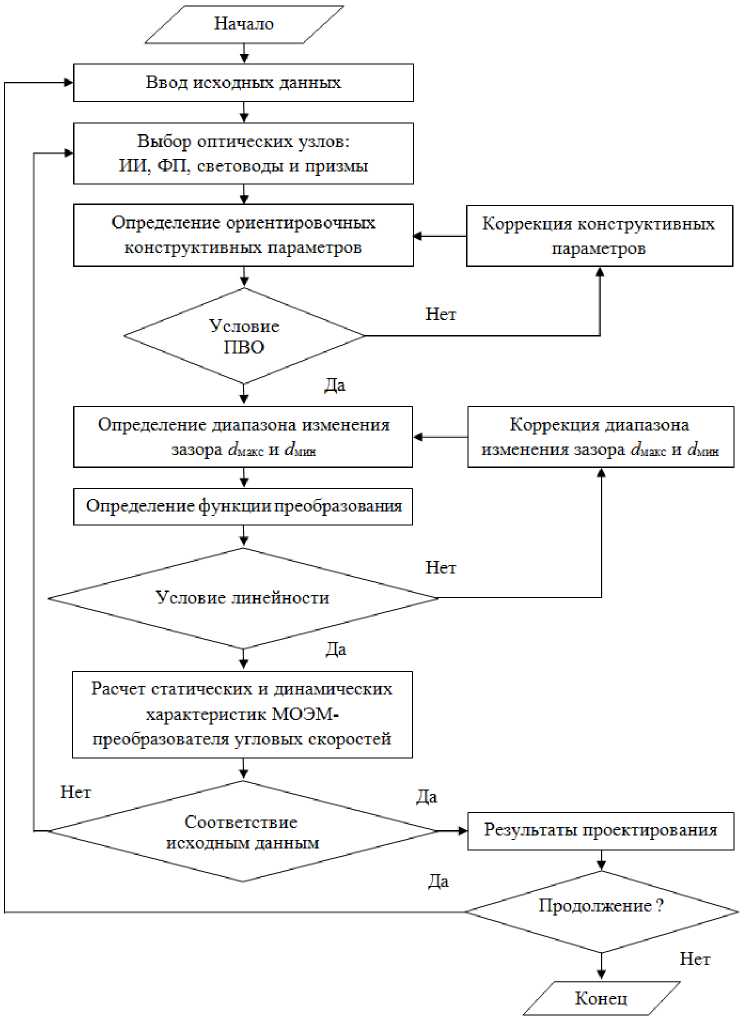
Рис. 1. Алгоритм расчета одноосевого МОЭМ-преобразователя угловых скоростей на основе ОТЭ

При рассмотрении задач разработки и расчета МОЭМ-преобразователя угловых скоростей допустимы следующие положения:

– ЧЭ симметричен и изготовлен из однородного пьезоматериала; центры масс недеформи-руемых дополнительных масс ЧЭ располагаются в их геометрических центрах на расстоянии l /2

от точки О , жестко закрепленной с корпусом МОЭМ-преобразователя угловых скоростей; величина прогиба конца ЧЭ линейно зависит от приложенных сил;

– диапазон рабочих температур от –50 до +80 °С; при этом температурные изменения модуля Юнга, пьезомодуля обратного пьезоэлектрического эффекта и также линейных размеров ЧЭ считаются линейными.

Выбор оптоэлектронных узлов и материалов

Источник излучения (ИИ), фотоприемник (ФП), ППВО и световоды для МОЭМ-преобразователя угловых скоростей должны быть совместимы по спектральным характеристикам с большими коэффициентами эффективного использования с малыми оптическими потерями, обладать долговечностью, сохранять работоспособность в диапазоне температур от –50 до +80 °С [7, 8].

В качестве ИИ могут быть использованы светодиодные модули, работающие в режиме генерации оптического излучения с длиной волны λ = 0,7…1,3 мкм, которые создают мощность десятки мкВт с малым коэффициентом потерь. Для поддержания стабильной излучаемой мощности ИИ на заданном уровне может быть применен модуль стабилизации оптического излучения, при котором часть потока от ИИ поступает в световод обратной связи, соединенной с ФП [9].

Основным требованием при выборе ФП является его соответствие спектральным характеристикам используемых ИИ, световодов и достаточный диапазон, в котором ток ФП пропорционален падающему потоку излучения. Для малогабаритных преобразователей целесообразно использовать кремниевые фотодиоды, имеющие достаточно линейную зависимость фототока от мощности падающего излучения, малую детектируемую мощность и высокую термостабильность.

Выбор пьезоматериала ЧЭ ограничен соображениями необходимой прочности, упругости, высокого пьезомодуля, малой гистерезисности, температурной стабильности и точкой Кюри. К таким пьезоматериалам могут быть отнесены: титанат бария BaTiO 3 , ниобат лития LiNbO 3 и цирконат-титанат свинца ЦТС-19 PbTiO 3 –PbZrO 3 . Материал эффективной поверхности ЧЭ с показателем преломления ( n ₃) выбирается таким образом, чтобы относительно него в призме ( n ₁) условие полного внутреннего отражения (ПВО) нарушалось раньше, чем относительно среды ( n 2 ) между призмой и ЧЭ, т. е. n 3 > n 2 [10].

ППВО и ЧЭ с дополнительной массой могут быть изготовлены из кварца и пьезокерамики соответственно, что позволяет снизить дополнительную погрешность, обусловленную изменением конструктивных параметров МОЭМ-преобразователя при повышенных температурах и обеспечить высокую чувствительность во всем диапазоне измерений.

При определении размеров ППВО необходимо учитывать, что основание ППВО должно быть больше ширины эффективной оптической поверхности ЧЭ. Отметим, что расходимость и неравномерность оптического излучения, выходящего из ИИ, приводят к тому, что при увеличении расстояния между торцами световодов ИИ и ФП все меньшая часть излучения попадает на входной торец ФП. Количественно оптические потери в устройстве можно выразить через коэффициент использования излучения η [9, 10]:

1       R (de/

n = 1 - exp 5 -p • СД

' P I /2 • аT

где β – постоянный коэффициент, зависящий от числовой апертуры и типа используемых световодов; а Т – расстояние между торцами световодов, измеряемое по ходу осевого луча; d С – диаметр световодов.

При использовании световодов с большой числовой апертурой светораспределение на торце световода ИИ становится шире и параметр β будет уменьшаться. Для повышения коэффициента использования излучения η требуется устанавливать максимальное приближение торцов световодов ИИ и ФП друг к другу ( d _С-/_- а _Т → 1), соответствующее минимально возможным размерам призм, определяемыми размером ЧЭ; для призмы необходимо использовать оптический материал с высокими показателями преломления [11].

Критерии для определения диапазона рабочих зазоров

Угол падения излучения θ на модулируемую поверхность необходимо выбирать таким, что при оптическом контакте призмы лишь с оптической поверхностью ЧЭ в нем нарушалось условие ПВО. Это значит, что угол ПВО θ1 должен удовлетворять условию arcsin (n2 /п)) < 01 < arcsin (n3 /n1).                                                                      (2)

Для уменьшения оптических потерь излучения, которое способно достигнуть торца ФП, критерий подбора угла падения θ определяется углом ПВО θ 1 и размерами призмы:

• 0 = 0i ± arc tg ^f d^CZ   1 .                                                                    (3)

• ¹            /2 • ^а T )

Чувствительность преобразователя к наноперемещениям, вызванным измеряемой угловой скоростью, определяется производной отражательной способности R [ d (Ω z ), λ, θ] структуры «ППВО – воздух – ЧЭ» по рабочему зазору d ( Ω z ) [12]:

S = — R Г d (Q_Z), ^ 011         .                                                    (4)

d d ( Q _Z ) ^{L v Z)     J|}^,0 = const

Отметим, что чувствительность S не постоянна в расчетном диапазоне измерения и меняется также от конструктивных параметров ( d 0 , θ, λ) (рис. 2). Проблема обеспечения квазилинейной функции преобразования, исходя из требуемого уровня чувствительности S , решается определе нием допустимого рабочего участка 2Δ d = d макс – d мин , где d макс и d мин – максимальный и минимальный зазоры между ППВО и ЧЭ. При этом допустимое уменьшение чувствительности S от носительно максимального значения задается параметром n , т. е. до S = S макс / n .

Основная погрешность МОЭМ-преобразователя зависит от диапазона изменения относительного зазора dмин/λ…dмакс/λ, т. е. от того, какой участок 2Δd выбран в качестве рабочего (рис. 3), и может определяться как

^ осн

² • R d 0 ^{( d} 0 , ⁰ , ^ ) R d мак с ^{( d} м акс , ⁰ , ^ ) R d мин ^{( d} мин , ⁰ , ^ )

R d макс ^{( d} ма к с , ⁰ , ^ ) R d мин ^{( d} ми н , ⁰ , ^ )

• 100%.

Максимальная основная п огрешность наблюдается при максимальны х отклонениях конца ЧЭ, соответствующих максимальным величинам угловой скорости Ω z = Ω макс , т. е. концам диапа зона изменения относительного зазора – точкам d мин /λ и d макс /λ. Для уменьшения основной по грешности целесообразно выбирать наиболее крутой участок 2 Δ d .

Полученный ориентировочный диапазон изменения зазора d макс и d мин необходимо уточнить путем возможного возрастания основной погрешности в результате смещени я начального зазора d 0 и осевого угла падения θ , откл онения геометрических параметров ЧЭ и до полнительных масс от номинальных значений. Для эт ого можно рассчитать характеристики МОЭМ-преобразователя при среднем квадратическом откло нении указанных параметров. В результате эт ой корр екции опреде ляются окончательные значени я максимального и минимального зазоров меж ду ППВО и ЧЭ.

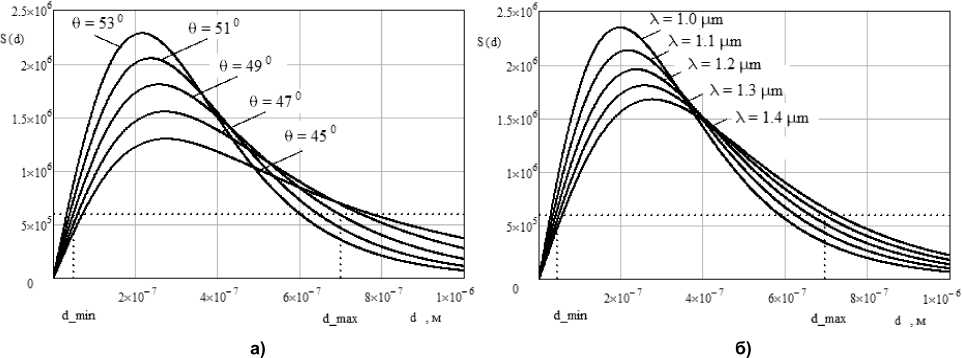
Рис. 2. Зависимости чувствительности МОЭМ-преобразователя от рабочего зазора при вариациях: а – угла падения θ излучения, б – длины волны λ

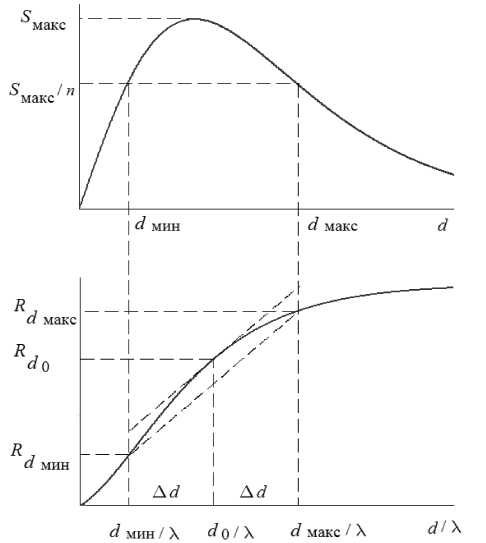
Рис. 3. К определению основной погрешности МОЭМ-преобразователя угловых скоростей

Критерии определения геометрических параметров и дополнительной массы ЧЭ

При расчете МОЭМ-преобразователя угловых скоростей на основе ОТЭ необходимо учитывать, что рабочий зазор d(Ωz) между основанием ППВО и ЧЭ не должен превышать длины волны оптического излучения и составляет сотни нанометров. Для обеспечения возможности функционирования МОЭМ-преобразователя амплитуды отклонений концов ЧЭ с учетом выбранного начального зазора d0 должны выбираться на основе скорректированного диапазона изменения зазора dмакс и dмин, т. е. значения геометрических параметров l, b, h и дополнительной массы m ЧЭ удовлетворяют следующим условиям [13, 14]:

d мин — ^<

d ₀

—

3 • to • ^p • d обр • U в_Озб m • Q z • I

2 • E • h h

'3 Г /

20 +

m

p-h •b_

— d макс ^.

макс

Величина длины l предварит ельно выбирается как можно меньшей, чтобы исключить вторую и выше формы изгиба ЧЭ, т. е. д олжно быть только угловое движение относи тельно точки закр епления ЧЭ , и удовлетворять огр аничениям по габаритным показателям, но д остаточной с точки зрения технологичности изготовления. Уменьшение величины длины ЧЭ l приводит к уменьше нию амплитуды вынужденного к олебания, что требует использования повыш енного напряжения возбуждения.

Минимальные величины толщины h и ширины b ЧЭ ограничиваются механической жесткостью конструкции и размерами оптического пятна, образующегося на основ ании ППВО от тех лучей, которые, отразившись, попадают на торец световодов ФП. Этим требованиям предвари тельно удовлетворяют величины l в диапазоне 1…10 мм, h и b – в 10…200 мкм [15, 16].

Д ля увеличения чувствительности S МОЭМ-преобразователя могут быть введены дополнительные массы m , расположенны е на двух концах ЧЭ. При этом следует учи тывать, что если установить большую величину m , то эффективный диапазон измерения умен ьшится, линейность функции преобразования ухудш ится и в критическом случае возможно нар ушение работосп особности устройства.

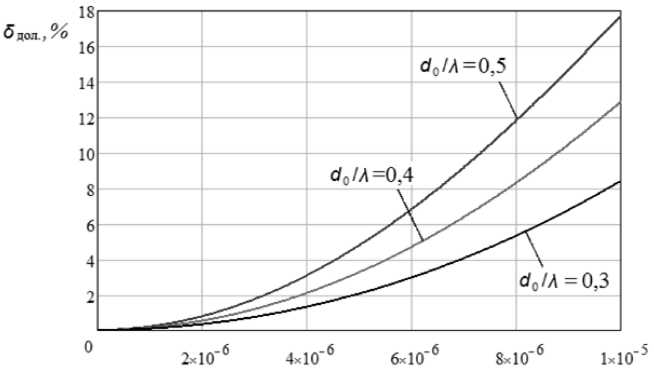
Получены зависимости д ополнительной нелинейности функции преобразования от величины m по схемой одноканального считывания при следующих параметрах: λ = 1,3 мкм, θ = 51°, и для ЧЭ: l = 5 мм, b = 90 мкм, h = 45 мкм (рис. 4). Поэтому определение величины m ЧЭ ограничивается выполнением условия дополнительной линейности функции преобразования.

т, кг

Рис. 4. Зависимости дополнительной нелинейности функции преобразования от дополнительной массы m

Кроме того, при определении дополнительной массы m должно быть выполнено условие ме ханической прочности по нормальным напряжениям σ макс при максимальном перепаде моментов, действующих на ЧЭ [17, 18]:

^ макс

^M 2 макс

Wr

C мин

<и,

где WC мин – наименьшее значение момента сопротивления сечения ЧЭ; [σ] = σмакс /nσ – предель- ное допустимое напряжение, σмакс, nσ – предел текучести и запас прочности материала ЧЭ, соответственно; M2 макс - максимальное значение суммарного изгибающего момента, действующего на ЧЭ, который можно определить как

2 макс

®' d об р ' U возб m ' l ' ^ Z 2 ' E ' h h

Р" b " h " l --+ m

.

С учетом ориентировочных геометрических параметров получим m <

^ ^имакс C мин           ^p        I

—

®' d обр ' U возб m "  l-^ ZZ       8

Назовем эти условия необ ходимыми критериями для подбора геометр ических параметров и дополнительной массы ЧЭ МОЭМ -преобразователя угловых скоростей на основе ОТЭ. Опреде ляемые параметры ЧЭ необхо димо настраивать и корректировать путем проверки допустимой не линейности функции преоб разования, работоспособности прибора с уч етом увеличения н а пряжения возбуждения и частоты колебания, воздействия ударно -линейных ускорений.

Программное обеспечение и результаты моделирования расчетаМОЭМ-преобразователя угловых скоростей на ОТЭ

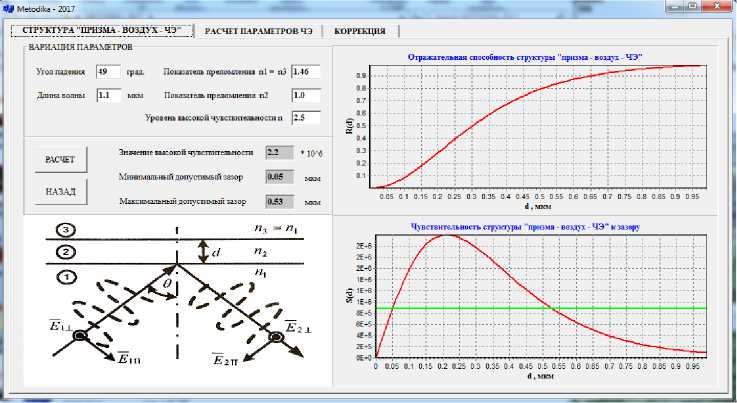
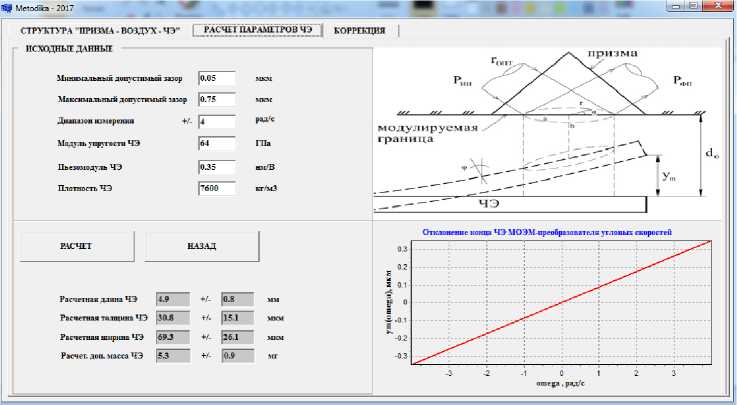
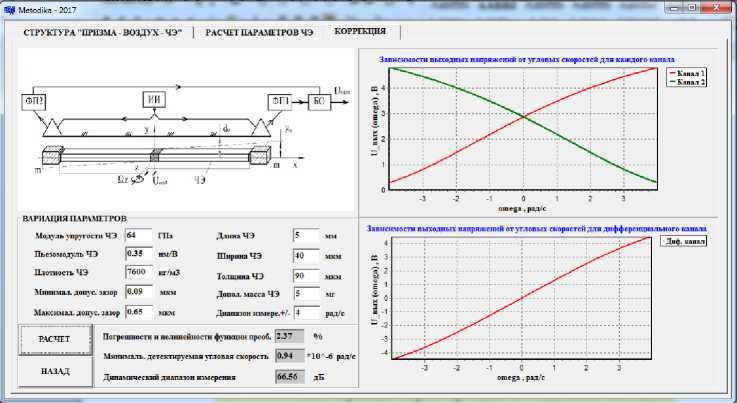
Разработано программное обеспечение в соответствии с алгоритмом расчета, по которому определяются основные параметры МОЭМ -преобразователя по заданным техническим требованиям (рис. 5).

Для примера укажем, что для следующих исходных данных: материал ЧЭ – ЦТС-19 ( E = 64 ГПа, d обр = 0,35 нм/В, ρ = 7600 кг/м ³), n 1 = 1,46, n 3 = 1,46, n 2 ≈ 1, диапазон измерения ±4 рад/с, нели нейность функции преобразования не более 1,5 %, параметр n = 3, погрешность не более 1,5 % на расчетном диапазоне изме рения, температурные погрешности не бол ее 1 % на диапазоне –50 °С…+80 °С получены: длина l = 5 мм, толщина h = 40 мкм и ширина ЧЭ b = 90 мкм, соответственно; θ = 49°; d 0 = 0,41 мкм; λ = 1,1 мкм.

а)

б)

в)

Рис. 5. Рабочие окна программного обеспечения: а – режим определения диапазона изменения зазора по заданному уровню чувствительности; б – режим расчета параметров по данным исходных требований; в – режим проверки и настраивания параметров

Выводы

В представленной работе предложена методика расчета одноосевого МОЭМ-преобразователя угловых скоростей на основе ОТЭ по заданным техническим требованиям, включающая алгоритм и реализованное программное обеспечение. Получены основные формулы и критерии, позволяющие определить основные параметры такого прибора, которые удовлетворяют данным исходных требований.

Результаты численного моделирования доказывают возможность технической реализации конструкции МОЭМ-преобразователя угловых скоростей на основе ОТЭ. При измерении малой угловой скорости, как правило, такой прибор имеет квазилинейную функцию с высокой чувствительностью, хорошие массогабаритные показатели и уровень энергопотребления, что обеспечивает его конкурентоспособность с другими датчиками и также возможность эффективного применения в достаточно жестких условиях сильных электромагнитных помех.

Статья подготовлена при финансовой поддержке РФФИ (грант № 16-08-00447-а).