Методика расчета определения водопотребления растений при использовании систем импульсного дождевания автоколебательного действия

В Азербайджанской Республике сельскохозяйственное производство ведется в сложных условиях. Большую часть территории республики составляют горные и предгорные районы, для которых характерно наличие крутых склонов с острым дефицитом естественной влаги в почве. Многообразие форм рельефа территории, климатические условия, распашка крутых склонов способствуют развитию эрозионных процессов. Под влиянием ветра и воды уносится наиболее плодородный аккумулятивный горизонт, питательные элементы, снижается содержание гумуса, затухают микробиологические процессы.

Для решения данной проблемы в первую очередь необходимо уточнить единицу методического подхода к обоснованию норм и нормативов водопотребления сельскохозяйственных культур, а также их корректирование.

Цель исследования

Целью исследования является разработка уточненной методики расчета для определения фактической нормы водопотребления сельхозкультур с применением малоинтенсивного орошения.

Основной задачей является определение водопотребления сельскохозяйственных культур (эвапотранспирация). Величина эвапотранспирации зависит от почвенно-климатических условий территории, вида и урожайности сельскохозяйственных культур, влажности почв, глубины грунтовых вод и др.

Вода, необходимая для эвапотранспирации растений в аридной зоне, не может быть восполнена только за счет естественного прихода влаги (атмосферные осадки, подпитки корнеобитаемого слоя почвы в результате капиллярного подтока из грунтовых вод).

Дефицит водного баланса, равный разности эвапотранспирации растений за вегетационный период и естественного прихода влаги, количественно составляет биологическую потребность растений в оросительной воде.

Задачи исследования: создание систем малоинтенсивного микроорошения и обоснование уточненной нормы подачи воды с учетом биологической потребности сельскохозяйственных культур.

Техника и технология полива сельскохозяйственных культур, а также гидромелиоративные системы, водозаборы, оросительные каналы и дренажные системы различного порядка обеспечивают подачу воды на поля и отвод дренажных вод.

Биологически потребные оросительные нормы зависят от уровня урожайности сельскохозяйственных культур, а значит, от плодородия почв и уровня агрокультуры сельскохозяйственного производства.

Ход исследования и обсуждение результатов

Обоснование норм водопотребления необходимо проводить на базе теоретического и практического анализа природных условий территории с учетом возделываемых культур.

Рис. 1 . Применение малоинтенсивного орошения

Объем выплеска V вып при каждом цикле с учетом подпитки подводимым расходом q в общем случае может быть установлен [5] из выражения:

VV вып      геом

P a

р , bn

P у -1 qQntde t

выб ,

где t выб – продолжительность выброса;

Р n – нижний предел давления в гидроаккумуляторе.

При постоянном расходе подпитки воды q продолжительность накопления определяется из простого выражения

V   РР

геом    аb нак   qпод  Pb  PH

Без учета подпитки продолжительность выброса воды приближенно можно установить из выражения выб

вы "РДНт^ ’ где Vвыб – объем выброса воды;

f с – коэффициент расхода сопла;

– площадь отверстия сопла;

H – напор при выбросе воды;

H – первоначальный напор воды.

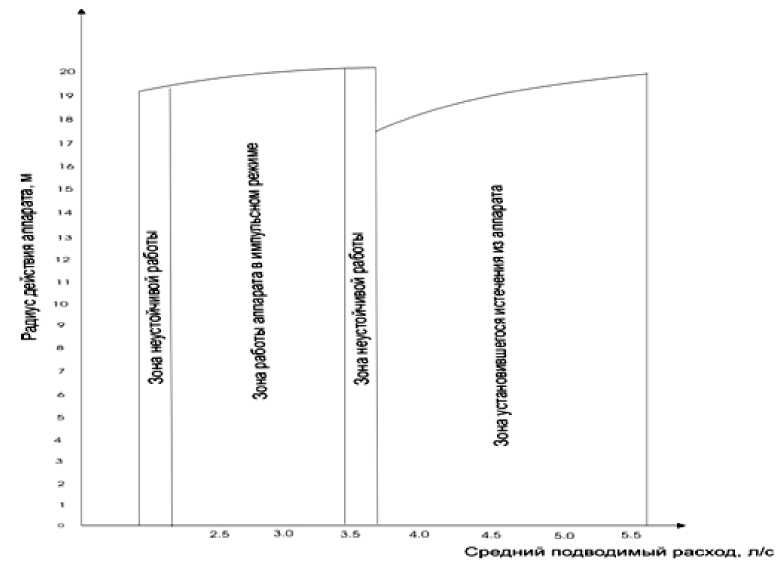
Рис. 2. Режим работы импульсного аппарата при различной величине подводимого расхода

Для решения проблемы водопотребления растений, а также уточнения методики расчета необходимо изучить водопотребление различных культур, обоснование закономерности кривой Вильямса и дать оценку режима работы самого дождевального аппарата автоколебательного действия [2; 5].

Следует отметить, что при импульсном орошении почвенные влагозапасы активного слоя влагообмена в засушливый период непрерывно поддерживаются на оптимальном уровне.

В соответствии с расчетами и опытными данными продолжительность выброса накопленного объема воды для среднеструйных импульсных аппаратов колеблется в сравнительно узких пределах 4–6 с.

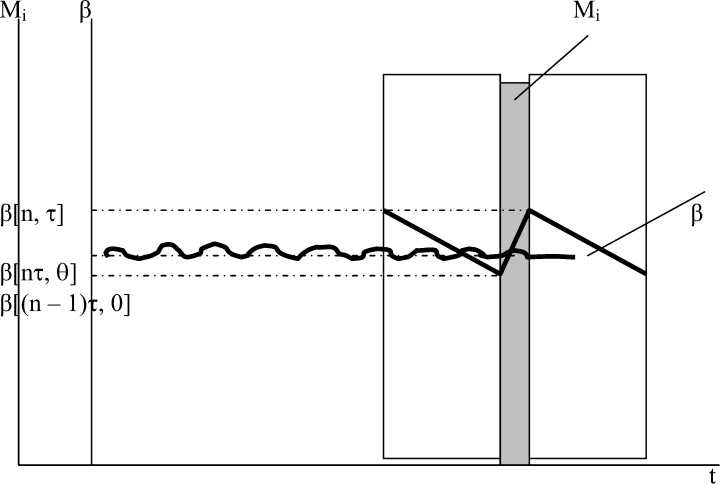
Рис. 3. График соотношения влажности и полива во времени

Величина влагопотребления может быть определена в любое время суток по кривой Вильямса. При снижении влагозапасов в слое активного влагообмена до оптимального уровня осуществляется дождевание в импульсном режиме. Это даст возможность по новой методике решить проблемы водопотребления растений. Особенности технологии полива импульсным дождеванием автоколебательного действия заключается в том, что возникновение дефицита почвенной влаги на поливных участках компенсируется ежедневной водоподачей [5].

Надо отметить, что текущее водопотребление растений, связанное с интенсивностью солнечной радиации и тепловых процессов, определяется по следующей формуле:

т — + T = 0. dt

Это уравнение описывает изменения температуры от рассвета до заката. После заката до рассвета изменения температуры описываются таким же уравнением первого порядка, но без правой части. Начальное уравнение – это уравнение (4) в момент солнца.

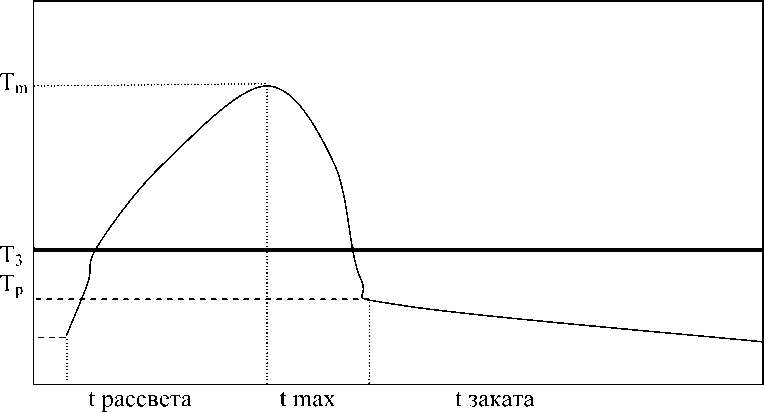
Рис. 4 . График водопотребления

Решение уравнения (4) имеет вид суммы общего решения однородного уравнения и его частного решения. Отсюда

t т (t) = c е + c2y,

где С 1 – постоянная интегрирования уравнения (9);

С 2 – постоянная интегрирования уравнения (9);

Y – частное решение (5).

Общее решение определяется решением однородного уравнения вида:

dX т--1- X = 0, где Х- общее решение. dt

Частное решение определяется решением неоднородного уравнения:

dY _v , .  (t(t-t_m )

т--1- Y kk sin —----— dt             2(tm-tp )

Пусть Y = C ₂ sin( at + ),,

” ⁽ t-t m ) ²⁽ tm-tp )

тогда C ₂ cos( at + (p ) + C ₂ sin( at + (p ) = k sin

Из этого уравнения очевидно, что at

(t tm)

^2(t m ^— t p )

Для определения постоянного интегрирования используем начальные условия вида:

T ( t p ) = T p и T ( t, ) = T, .

Из них следует:

T kR

t t _p

T p e

tm tp т -T e T m pe

sin

(t tp)

^(t m- t p )

.

Модель кривой водопотребления отличается при принятых допущенных временем чистого запаздывания h .

Из вышеизложенного следует, что выведенная математическая модель и расчет дадут возможность правильно оценить режим работы импульсного дождевального аппарата автоколебательного действия и регулировать частоту импульсов [7].

В промежутке от заката до рассвета температура определяется процессом остывания растения от температуры заката.

t 3            tp

E_v    B_Rdt    B_odt .

tp           t 3

Учитывая выражение (6), подставим его в

требления за сутки.

(7) и получим при этом величину водопо-

Здесь

J _ 2(t m    t p )

V cos

t 3 t 3

2(t 3- t p )

cos

tp             tp h cos

2(t 3- t p ))    2(t 3- t p )

sin

v

t 3 t 3

2(t 3- t p )

sin

tp

2(t 3- t p ),

t p h sin

2(t 3- t p )

Идентификация чистого запаздывания h и коэффициента пропорциональности m производится на основании уравнения Е v .

Таким образом, уравнение температуры определяется следующими измеряемыми па- раметрами:

временем достижения максимума температуры временем рассвета временем заката интенсивностью солнечной радиации температурой растения на рассвете температурой растения на закате максимальной температурой

Неизвестна величина k – коэффициент пропорциональности температуры интенсивности радиации. Идентификация величины k производится из уравнения T [4]. Идентификация чистого запаздывания h и коэффициента пропорциональности m производится на основании уравнения E v .

Текущее влагопотребление растения W пропорционально его температуре Т. Однако температура растения Т пропорциональна интенсивности солнечной радиации ввиду инерционности тепловых процессов, как апериодическое звено [3; 7]. Процесс описывается дифференциальным уравнением т dT + T = kR( t), (9)

dt где Т – температура растения;

R – интенсивность солнечной радиации в зависимости от времени суток t ;

k – коэффициент пропорциональности установившегося значения (стационарной величины) температуры растения величине солнечной радиации;

– постоянная времени температуры растения, характеризующая ее инерционность.

Интенсивность водопотребления W связана с температурой через звено чистого запаз-

дывания:

W ( t ) = T ( t – h ),                                         (10)

где h – время чистого запаздывания, в течение которого отсутствует реакция водопотребле-

ния на изменения температуры. С учетом (7) имеем:

dW .    ,   .

т — + W = kmR( t-h ) , dt

где m – коэффициент пропорциональности величины водопотребления значению температуры.

При этом , h , k и m зависят от массы растения, то есть от момента времени вегетации. Исходя из этого, получим следующие выражения:

= aM ; k = bM ; h = cM ; m = dM ,                        (12)

где M ( t ) – масса растения в момент t;

а , b , c , d – коэффициенты пропорциональности.

К моменту сбора урожая М близка к установившемуся значению М е . Изменения М можно предположить подчиняющимися дифференциальному уравнению первого порядка:

¹ d^M     ™

M M, de где Ме – конечная масса растения;

= t – T b – время с начала вегетации, то есть время возрастания массы растения.

Из (12) следует:

M ф) = Me (1- e"^{a y}) ;

t = a (1- e~“ ⁹MM_e ;

k = b (1- e"“ ⁹M M e ;

h = c (1- e’“ m M e ;

h = c (1- e"^a9) M .

Эти выражения объясняются тем, что по мере приближения к концу вегетации Т е рост растения замедляется, а к моменту уборки урожая масса растения достигает стационарного значения [2; 6].

Предположим, что уборка урожая целесообразна, когда масса растения практически перестает возрастать. Тогда

1 — e =д и e =1 — О .

Отсюда имеем: при = Т е времени сбора урожая уравнение для определения:

_ ln(1-^)

T e

,

здесь и далее Т e – время начала вегетации.

Уравнение (13) справедливо не всегда.

Для ряда культур возрастание массы происходит не во всех фазах. Тогда вместо Т е рассматривается последняя фаза, в которой происходит набор веса.

С учетом того, что солнечная радиация имеет гармоническую зависимость от времени суток, можно принять, что в общем виде дифференциальное уравнение кривой температуры растения будет иметь вид

т T-тТ = kA sin dt

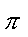
12( t з -tp )

⁽ t-t m )

где t p – время рассвета;

t з – время заката;

А – амплитуда солнечной радиации;

t – текущее время;

t m – время момента достижения максимальной температуры.

Это уравнение описывает изменения температуры от рассвета до заката.

После заката до рассвета изменения температуры описывается таким же обыкновенным дифференциальным уравнением первого порядка, но однородным, без правой части:

dT ■ +T 0 . dt

Начальное условие его – это решение уравнения (15) в момент заката солнца, то есть Т ( t з ).

Решение уравнения (16) имеет вид суммы общего решения однородного уравнения и его частного решения:

T ( t ) Ce ^t C y ,

где С 1 , С 2 – постоянные интегрирования уравнения (18);

у – частное решение уравнения (18).

Частное решение определяется решением неоднородного уравнения (17).

dY

T— + Y k sin< dt

71 ( t   t_m )

2( t_m   t_p )

.

Пусть Y C sin( at^Ф ), тогда

C cos( at^Ф )+ C sin( at ^Ф )   k sin<]

L ( t t_m ) 2( t_m t_p )

.

Из этого уравнения очевидно, что

_Qt^ф=, ( t tm )

2( t m t p )

.

Для определения постоянных интегрирования используем начальные условия вида T(tp)  Tpи T(tm)  Tm, из них следует, что начиная от времени рассвета до момента достижения максимальной температуры кривая температуры растения будет описываться выражением

T  kR <

t t p                    t m t p

T p e"^r   - ( T_m  T_p e " ^T )sin

71 ( t   t_p )

2( t m    t p )

p

Модель кривой водопотребления отличается при принятых допущениях временем чистого запаздывания h .

В промежутке от заката до рассвета температура определяется процессом остывания растения от температуры заката:

T kR

t 3 t p                   t m t p

T p e"^r   - ( T_m  T_p e " ^r )sin

^( t ₃    t_p )

2( t_m   t_p )

p .

Идентификация величины k производится из уравнения Т при остальных известных константах, входящих в уравнение (9). Это достигается подбором k при каком-либо известном значении Т.

Процесс водопотребления в целом описывается уравнением t3                 tp

E v = J E v^R ( t ) dt + J E v^c ( t ) dt , t p                  t 3

где E_v ^R – влияние нагрева под действием радиации;

E_v ^c – охлаждение за промежуток между закатом и рассветом.

Учитывая выражения (21) и (22), поставим их в (23) и получим при этом величину во- допотребления за сутки:

¹ 3                       -

Ev   mkR Tpe tp

t t _p                        t _m t _p

(Tm  Tpe      )sin

(t tp )

²⁽³т-³ р )

t _p                t

>d1-\- ^(3 ₃ )e ^Tdt =

mkR

t_p h      t_p       t_p                   t_m  t_p

T_p^T(e"^ -ё^V(T_m Tp^pe^-^ )

_ tp     t 3

1 ₁₊ tT ( 1 3 )( e  - -e' ).

Заключение

Результатами исследования выявлено, что величина влагопотребления может быть определена в любое время суток по кривой Вильямса. Вместе с тем, при снижении влагозапа-сов в слое активного влагообмена до оптимального уровня осуществляется дождевание в импульсном режиме. Это дает возможность по предложенной новой методике решить проблемы водопотребления растений.