Методика расчета параметров лесных пожаров как динамических процессов на поверхности Земли с использованием данных космического мониторинга

Одной из областей, где требуется применение методов математического моделирования и теории управления, является охрана и рациональное использование природных ресурсов. Объекты, принадлежащие этой области, характеризуются, как правило, распределенностью в пространстве и зависимостью от большого числа трудно контролируемых факторов.

Особую группу составляют объекты, имеющие характер подвижных множеств или плоских волн на поверхности Земли. Примерами могут служить лесные и степные пожары, зоны загрязнения земной и водной поверхности, области, пораженные вредителями растений, зоны почвенной эрозии и опустынивания. Важность изучения таких объектов возрастает в связи с ростом антропогенной нагрузки на биосферу, процессами изменения климата.

Перечисленные объекты имеют разную физическую природу, различные пространственные и временные масштабы, но при определенных допущениях их динамика, в том числе процессы управления ими, могут быть описаны единым образом. Наиболее полно круг проблем, связанных с изучением этих процессов, актуальность таких исследований, их цели и задачи можно показать на примере лесных пожаров.

Задача охраны лесов от пожаров является весьма актуальной во всем мире в настоящее время. Так, в Российской Федерации по данным информационной системы дистанционного мониторинга федерального агентства лесного хозяйства (ИСДМ-Рослесхоз) за пожароопасные сезоны 2008 и 2009 гг. произошло 35 337 пожаров, огнем пройдено 15 565 510 га, в том числе 9 772 782 га покрытых лесом площадей [1]. Поскольку лес является одним из важнейших стратегических ресурсов, задача охраны лесов от пожаров, и в том числе моделирование и прогнозирование распространения пожаров, является чрезвычайно важной задачей. К настоящему времени разработано достаточное количество математических моделей распространения лесных пожаров и базирующихся на их основе методов прогнозирования. Эти модели и методы содержат разные подходы к рассмотрению процесса горения в природном пожаре, однако их общей особенностью является высокая требовательность к информационному обеспечению моделирования, т. е. условием построения адекватной модели и, соответственно, прогноза, является точное знание множества характеристик местности, на которой происходит пожар, состояния растительных горючих материалов, погодных условий. На текущий момент создать информационную базу для обеспечения построения прогнозов на основе таких моделей в России не представляется возможным.

Наиболее полная информация о лесопожарной обстановке на данный момент содержится в ИСДМ-Рослес-хоз. Эта информационная система существует и развивается с 1995 г. Источниками информации, представленной в ИСДМ-Рослесхоз, являются данные космического, авиационного и наземного мониторинга лесных пожаров. Причем, ввиду обширности зон наблюдения, методы космического мониторинга играют ведущую роль. В сборе данных участвуют спутники серий NOAA, TERRA, AQUA, SPOT, LANDSAT ETM+, МСУ-Э [1].

Наличие достоверного прогноза распространения и развития лесного пожара позволяет оценить угрозу природной среде, объектам экономики и населенным пунктам, принять необходимые меры по предотвращению ущерба, спланировать работу противопожарных сил. Одним из важнейших моментов при прогнозировании лесного пожара является построение его контуров. В настоящей работе представлена методика расчета контуров крупных (площадью более 200 га) лесных пожаров на основе ограниченной информации, доступной в ИСДМ-Рослесхоз [2; 3].

Наиболее полная информация, доступная в ИСДМ-Рослесхоз и базах данных территориальных авиабаз, связана с динамикой изменения площади лесных пожаров. Поэтому моделирование процесса распространения пожара целесообразно начинать с этого показателя. При моделировании конфигурации пожара удобно использовать принцип Гюйгенса, описывающий распространение волн в анизотропной плоской среде.

Данная методика может быть использована для моделирования других динамических процессов, упомянутых выше.

Исходные допущения. Были приняты следующие допущения:

• 1.    Динамика изменения площади пожара определяется выражением

• 2.    Скорость фронта пожара в соответствии с принципом Гюйгенса представляется как v ( ф, т ) = v ₀ ( t ) ^ ( ф ), где v ₀ ( t ) -подлежащая определению максимальная скорость распространения фронта пожара (например, в направлении ветра); ^ ( ф ) (| £ | <  1) - индикатриса полной скорости фронта, определяющая конфигурацию пожара; ф - направление распространения (0 < ф <  2 п ). Таким образом, в общем случае

S ( t ) = к о ( t - t o ) ^a ,                     (1)

где t - текущее время, сут; t ₀ - время возникновения пожара, сут; a - показатель динамики пожара; k ₀ - постоянный коэффициент имеющий размерность га/сут ^а . Как ясно из геометрических соображений и будет показано ниже, с показателем а связано также изменение скорости фронта пожара: при a = 2 скорость фронта пожара постоянна, при a < 2 эта скорость со временем уменьшается, а при a > 2 - скорость возрастает.

v 0 = v 0( w, t), ^ = ^( wф), где w - величина скорости ветра, м/с. Там, где это не требуется, зависимость от w опускаем.

Индикатриса определяется скоростью и направлением ветра, она принимается неизменной в расчетный период времени; угол ф в приведенных ниже формулах отсчитывается от направления ветра по часовой стрелке.

Формулы для расчета скорости фронта пожара. Для упрощения формул в данном разделе положим t ₀ =0. Рассмотрим элементарное приращение площади dS . На рисунке показана кромка пожара в два близких момента времени t и t + dt . Из рисунка следует, что dS = v n dtdl , где v n - нормальная скорость фронта; dl - приращение длины контура, которое вычисляется по формуле [4]

t dl = ldф = dф^2(ф) + ^2(Ф) J v0 (т)dт .        (2)

В свою очередь, нормальная скорость связана с полной скоростью соотношением

V n (ф^) = _**.0_ = ^V ' t       .

1 + ₍ ©фО ) 2 ^² ( ф ) + ^‘ ²( ф )

V       V (ф, t )

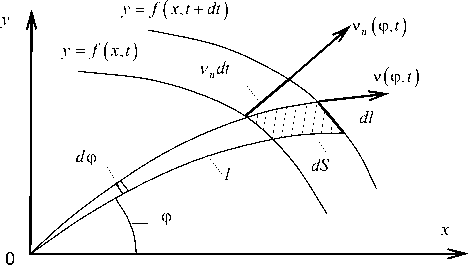
К выводу формулы скорости фронта пожара

Отсюда

t dS = dфdtv0(t)^2(ф)J v0(т)dт .

Приращение площади по всем направлениям распространения dS 2п = j" dSd ф = 2dtv 0 (t )J d ф^2 (ф) J v 0 (т) d т.

0                         00

Скорость прироста всей площади пожара dS          π

• — = 2v0(t)J§ (ф)dфJv0(т)dт ,(3)

dt           00

а динамика общей площади примет вид

π t π

S ( t ) = 2 J ^ ²( ф ) d ф J v 0© J v o© d ^ d т .

0             00

Рассмотрим теперь закон изменения скорости фронта пожара. Будем искать функцию v0(t) в виде v0S(te), где величины р и v0S подлежат определению. Тогда интеграл по времени в уравнении (3) будет равен t1

f v 0(т) d т = -v0 Ste+1, а скорость прироста площади dS = 2     t2p+1 Г^2(ф) d ф dt р +1

С другой стороны, из первоначального предположе- ния S(t) = k0ta следует dS

— = k _n a t dt ⁰

откуда получаем уравнение 2

2     12в+Ч ^2(ф) d ф = к0a ta-1.(4)

e +1

Приравняв в уравнении (4) показатели степени при t, получим 2p + 1 = a - 1, откуда e=У -1

Далее, приравняв множители при t , определим величину v _{0 S} :

_{= (} a k ₀( β+ 1) ₎ 1/2 ₌ a k 0 ₌a k 0

^{0 S  ππ} 2 P ( w )^{,  (5)}

2∫ξ2(φ)dφ      2∫ξ2(φ)dφ

00 где

P ( w ) = ∫ ξ ²( w , φ ) d φ .

Формула (5) есть искомая формула для расчета скорости пожара.

На основе формулы (2) можно вычислить также периметр горящей кромки пожара. В частном случае, когда пожар развивается из очага малого радиуса (точечного очага)

L ( t ) = 2 ∫ ^π ld φ= 2 ∫ ^tv ₀( τ ) d τ ∫ ^π ξ ²( w , φ ) +ξ′ ²( w , φ ) d φ .

Формула для скорости прироста периметра пожара примет вид dL(t)=2v0(t)Q(w),                (6)

dt где             π

Q(w) = ∫ Vξ2(w, φ) + ξ′2(w, φ)dφ.

Индикатрисы скорости фронта. Рассмотрим конкретные выражения для индикатрис.

Экспоненциальная индикатриса равна [4]

ξ(φ) = exp(a(w)(cos(f)–1)), где a(w) – коэффициент, зависящий от скорости ветра: a(w) = 0,785w – 0,06w2.

Формула справедлива при условиях 0 ≤ w ≤ 3 м/с. Тогда интегралы, стоящие в выражениях (5) и (6), примут вид

π

P ( w ) = ∫ ξ ²( w , φ ) d φ =

π

= exp( - 2 a ( w )) ∫ exp(2 a ( w )cos( φ )) d φ , 0

π

Q ( w ) = ∫ Vξ ²( w , φ ) + ξ′ ²( w , φ ) d φ =

π

= ∫ ξ ( w , φ )1 +

a ⁴( w )    ₂

₄ sin² (2 φ ) d φ .

Вычисленные величины этих интегралов для некоторых значений скорости ветра приведены в табл. 1.

Эллиптическая индикатриса равна

_{ξ (} φ _{) =}     1 - e ( w )    _,

1 - e ( w ) cos( φ )

где e ( w ) – эксцентриситет эллипса, зависящий от скорости ветра.

Для оценки зависимости эксцентриситета эллиптической индикатрисы от скорости ветра были аппроксимированы эллипсами графики индикатрис, приведенные в работе Ф. Альбини [5], для большого диапазона скоростей ветра и вычислены соответствующие эксцентриситеты. Была получена следующая аппроксимация зависимости эксцентриситета от скорости ветра:

e ( w ) = 1 - exp( - 0, 4 w ).

Затем были вычислены значения интеграла P ( w ) и Q ( w ). Результаты расчетов приведены в табл. 2.

Сравнивая данные табл. 1 и 2, можно увидеть, что значения функций P(w) и Q(w) для обеих индикатрис заметно различаются при одних и тех же скоростях ветра. При этом следует учитывать, что в первом случае скорость ветра вычислялась на высоте двух метров от земли, а во втором – на высоте десяти метров, и этим также объясняется более вытянутая форма эллиптической индикатрисы.

Погрешность предлагаемой методики. Понятно, что погрешности всех исходных данных вносят погрешность в конечный результат. В данной работе мы ограничимся простейшим расчетом погрешностей, связанных с оценкой площади пожара и его суточного прироста. Более точный расчет потребует привлечения законов распределения переменных.

Пусть погрешность определения площади пожара составляет δ S га. Рассмотрим вызванные этим погрешности параметров модели (1). Погрешность в оценке коэффициента k

ax

δS=∂S δk=taδk,

∂t откуда ta

Погрешность в оценке времени распространения пожара:

ax

δS=∂S δt = kata-1δt,

∂t откуда

Таблица 1

Значения интегралов квадрата экспоненциальной индикатрисы в зависимости от скорости ветра

w , м/с	0	0,1	0,2	0,5	1,0	2,0	3,0
a( w )	0	0,078	0,155	0,378	0,725	1,33	1,815
P ( w )	3,142	2,705	2,361	1,1695	1,178	0,818	0,686
Q ( w)	3,142	2,911	2,708	2,234	1,758	1,455	1,535

Таблица 2

Значения интегралов квадрата эллиптической индикатрисы в зависимости от скорости ветра

w , м/с	0	1,25	2,5	5	10	15
e ( w )	0	0,393	0,632	0,865	0,982	0,998
P ( w )	3,142	1,469	0,782	0,588	0,539	0,193
Q ( w)	3,142	2,151	1,60	1,424	1,379	1,194

δ S δ t =           .

k a t ^{a- 1}

Погрешность в оценке показателя a :

AS

δS=∂S δa =kta lntδa, ∂a

откуда

δa=

δS kta ln t .

Из формул (7)–(9) видно, что погрешности всех переменных, от которых зависит модель (1), зависят от времени и уменьшаются с ростом t .

Численный пример расчета скорости распространения пожара. Зарегистрированный в системе ИСДМ-Рос-лесхоз пожар К-1002 действовал в Идринском лесничестве Красноярского края с 10.05.2008 г. по 16.05.2008 г. Пожар был зарегистрирован на площади 393 га, площадь ликвидации 1163 га. Температура воздуха была 22,7 град., скорость ветра – 1 м/с, направление ветра – 180 град.

Примем, что погрешность определения площади составляет δ S = 100 га, Δ t = 16 – 10 = 6 сут. Принимаем показатель скорости роста площади пожара a = 2, т. е. предполагаем, что скорость фронта пожара постоянна.

Вычислим коэффициент k и его погрешность в модели: K = Δ S / Δ t ² = 770/36 = 21,4 га/сут², δ k = 100/36 = 2,7 га/сут ² .

Оценка погрешности коэффициента a по формуле (9)

дает величину

δa=

21,4 ⋅ 6² ⋅ ln6

= 0,07.

Поскольку скорость ветра невелика, воспользуемся экспоненциальной индикатрисой. Для скорости ветра w = 1 м/с по табл. 1 определяем множители P ( w ) = 1,178 и Q ( w ) = 1,758.

В соответствии с формулой (5), переведя гектары в

квадратные метры, получим

^v 0 S

k

P ( ω )

21, 4 ⋅ 10⁴

1,178

= 426 м/сут.

С учетом возможной погрешности δ k величина скорости фронта будет находиться в следующем диапазоне: 275 ≤ ν _{0 S} ≤ 577 м/сут.

По формуле (6) можно оценить скорость прироста периметра пожара:

^{dL ( t )} = 2 v ( t ) Q ( w ) = 2 ⋅ 426 ⋅ 1,758 = 1498 ± 531 м/сут. dt

Полученная оценка скорости фронта пожара в сочетании с выбранной индикатрисой распространения позволяет строить прогнозные оценки контура пожара через определенное время.

Представленная в статье простая методика оценки параметров процесса распространения, основанная на использовании геометрической модели, позволяет осуществлять прогнозирование распространения лесных пожаров, исходя из информации, хранящейся в ИСДМ-Рослесхоз. В методике используются индикатрисы двух видов , в зависимости от скорости ветра в районе пожара: экспоненциальная и эллиптическая. Полученные формулы применены для численного расчета параметров реального пожара, оценены их погрешности. Описываемый метод расчета применяется для построения контуров пожаров на основании нейросетевых прогнозов в программном комплексе «Тайга-2» и в разработке информационной системы прогнозирования лесных пожаров для ИСДМ-Рослесхоз.