Методика расчета съема металла при гидроабразивной обработке

Введение. Развитие машиностроения на современном этапе невозможно без постоянного повышения производительности труда и улучшения качества выпускаемых изделий. В машиностроении все более широкое применение находят методы обработки абразивным инструментом. Абразивная обработка позволяет обеспечить требуемые точность и качество деталей при высокой производительности, а также высокую надежность и долговечность машин в процессе эксплуатации.

В современном машиностроении существует потребность создания новых методов для обработки фасонных поверхностей, одним из методов обработки свободными абразивами является гидроабразивная обработка. Метод гидроабразивной обработки (ГАО) обладает высокими технологическими возможностями, он может использоваться для различных видов обработки, например, для: скругления острых кромок и сопряженных радиусов; полировки и шлифовки сложных поверхностей; удаления заусенцев и зачистки сварных швов; снятия со всей поверхности или локально дефектного слоя; подготовки поверхности под покрытие; снятия небольшого припуска с целью снижения шероховатости поверхности; удаления окисных пленок, нагара, различных повреждений с поверхностей деталей. При этом обеспечиваются высокая производительность и хорошее качество поверхностного слоя деталей.

Процесс струйной ГАО заключается в направлении струи суспензии, состоящей из воды и частиц абразивных материалов, на обрабатываемую поверхность заготовки. Эта струя подвергается воздействию потока сжатого воздуха, который увеличивает скорость истечения суспензии из сопла. В результате такой обработки образуются чистые матовые поверхности, без направленных рисок, характерных для лезвийной обработки материалов.

Механизм единичного взаимодействия. При исследовании основных технологических параметров обработки свободными абразивами одним из важнейших является вопрос теоретического моделирования процесса единичного взаимодействия частиц абразива с поверхностью обрабатываемой детали.

Воспользуемся методикой Е.Ф. Непомнящего [1] при исследовании трения и износа под действием потока твёрдых сферических частиц.

Пусть абразивная частица, имеющая характерный размер R (радиус описанной окружности), движущаяся со скоростью V 0 под углом р к поверхности детали, ударяется о нее с силой, достаточной для снятия стружки. Обозначим dV - объем металла, удаленного на пути скольжения dx, V _g - деформированный объем при взаимодействии сферической частицы с деформируемым пространством.

V

dV = — • dx,                            (1)

L где L - средний диаметр пятна касания при ударе.

Воспользуемся соотношениями, известными из теории скольжения жесткой сферы по пластически деформируемому полупространству [2]:

L = 2 4нк ;                                      (2)

V = n Rh ² .

где h – глубина внедрения частицы. Тогда:

dV =

n Rh h

2 Rh

dx ^;

dV = - Rr ■ h ³² dx .

Проинтегрировав (4) по пути скольжения частицы, получим:

v =-Rr ■

x _*

J h 2 d dx,

где x – путь частицы вдоль детали; x * – предел интегрирования обозначающий длину следа.

Известно [3], что при одних и тех же условиях микрорезания единичным абразивным зерном с повышением пластичности материала увеличивается количество металла, пластически оттесненного по краям царапины, и уменьшается доля металла, который удаляется в виде микростружки. Количественная оценка этого явления – коэффициент стружкообразования.

k_c = ^{V c}

ц где Vc – объем металла, удаленного в виде микростружки; Vц – теоретический объем царапины. С учетом вышеуказанного можно записать:

x _*

V =-■ kc ■ RR ■ fh32 dx.

c

Для нахождения предела интегрирования введем безразмерные координаты:

hx e =---- и L =, maxmax где hmax – максимальная глубина внедрения частицы.

После преобразований получим:

e . ( 5 . )

V = -kcRR■ h52    d833.

^c 0

Пределы интегрирования, полученные как указано выше, характеризуют размеры следа.

Опишем взаимодействие жёсткой частицы с деформируемым полупространством системой уравнений:

d2h m ■—y= PN; dt2

d2x m ■-7T = -PT, dt2

где m – масса частицы, кг;

m = — ■ n ■ D ³ ■ p ,                                   ⁽⁹⁾

6 ^ч

D – диаметр частицы, м; ρ ч – плотность материала частицы, кг/м³; t – время взаимодействия, с; P N – нормальная, а P τ – касательная составляющие силы взаимодействия частицы с полупространством, действующие только в течение времени взаимодействия t .

Решение первого уравнения системы (8) можно найти, используя известное соотношение из теории пластического контакта гладкого сферического индентора с деформируемым полупространством [1]:

P_N = π R h c σ _s ,                                     (10)

где R – радиус частицы; с – коэффициент несущей способности контактной поверхности, c=1÷6 для материала в нормальном состоянии, c=10 при наличии наклёпа; σs – предел текучести материала.

Тогда решение системы представляется следующим образом: d2h m ⋅     = -π⋅ R ⋅ h ⋅c ⋅σ , dt2                     s d2h     π⋅R⋅h⋅c⋅σs

=- dt2          m

Подставив значение массы, m получим:

d2h     3 c⋅σ ⋅h s.

= dt2     4 ⋅ρч ⋅ R2

dh

Откуда, учитывая, что при t = 0 h = 0 и     = υ 0 ⋅ sin α , получим:

dh                  3 ⋅ c ⋅ σ

= ± υ ₀ ⋅ sin β - ⋅ ^s ⋅ h ^{2 ,} dt ⁰          4 ⋅ ρ ч ⋅ R ²

где v 0 – скорость движения частицы.

dh

Проинтегрировав с учётом h=hmax,     = , получим максимальную глубину внедрения частицы:

h = 2 ⋅ R ⋅ υ ⋅ sin β ⋅        ρ ^ч     .                             (¹⁴)

max           0

\ 3 ⋅ k_s ⋅ c ⋅ σ_s

Для того чтобы учесть влияние сухого и гидродинамического трения на процесс формирования остаточного отпечатка, а также на параметры упрочнения поверхностного слоя, в дальнейшем введем коэффициент КТ, учитывающий условия взаимодействия в зоне контакта частица – тело. Тогда зависимость для hmax примет вид h =2⋅K ⋅R⋅υ ⋅ sin β⋅       ρч     .                        (15)

max          T        0

\ 3 ⋅ k_s ⋅ c ⋅ σ_s

Для определения скорости частиц при их движении в потоке воздуха или жидкости применимы законы гидродинамики [4]. Используя известную зависимость гидродинамики, величину скорости истечения смеси через отверстие или насадку под давлением можно представить в следующем виде:

υ см

2Л дин ,

ρсм

где Р дин – динамическое давление смеси, Па; ρ см – плотность рабочей смеси жидкости и частиц кг/м³; v 0 можно приравнять к v см .

Таким образом, hmax с учётом (15) и (16) определится по формуле hmax =2⋅KТ ⋅R⋅sinβ⋅

2 P_дин ⋅ ρ _ч

.

\ 3⋅ c ⋅ σ _s ⋅ ρ _см

Перейдя к безразмерным координатам, можно записать:

— = ±V₀ sin в V 1 — 8 2 ;

dt ⁰

dt = ±

h max

dε

V ₀ sin в 1 — ^{8 2}

Учитывая, что P _T = f • P N , где f - коэффициент пропорциональности,

преобразований получим

I d ^ = f ±

V

cg — f ,

d 8 .

после

Здесь знак плюс соответствует увеличению внедрения (де ^ 0), а знак минус - уменьшению (d8 ^ 0). Используя (18), можно проинтегрировать (7). Предел интегрирования 8* находим из условия, что скольжение прекращается либо когда dh = о, либо когда 8 = 0. В dh первом случае из (18) имеем

*

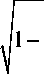
V ftg в

—

,

во втором случае 8 * = 0 .

8 * 3

Вид интеграла a = j ₈ 2 d ^ , входящего в выражение (7), зависит от численного значения 0

8*, т.е. от величины произведения f"tgв. Учитывая, что по данным [2] коэффициент трения абразивного зерна по металлу равен в среднем 0,25, а угол встречи с поверхностью детали для обработки свободным абразивом в основном не превышает 45°, можно сделать вывод, что f" tgв ^ 2.

8 * 3

Тогда интеграл A ■ = j ₈ 2 d ^ преобразуется к виду

A ■ = 2 ( ctg в — f )j- 8 2 d S ₂.                            (20)

0 V1 — 8 2

Интеграл, представленный в выражении (20), не берется в конечном виде, но его можно выразить через гамма-функцию:

Г I 5 1

A■ =Vk V J(Ctgв — f).                             (21)

ГI 7 I

V 4 J

Подставив значения гамма-функции, получим:

A ■ = 1^75 " ( Ctg в — f ) .                                     (22)

Подставив (22) в выражение (7), после преобразований получим зависимость для определения объема металла, удаленного за один удар абразивной частицы:

V = 15,5 k_c • R ³ R_T • sin в V

² P . • Р ч

A 2 (

—

V ³ ' ^C ' ^ 5 ' Р см J

V tg ^e

f .

Соответственно съем металла за один удар абразивной частицы q = 15,5kc • R KT • sin в V

^{2 Р} дин " ^рч

' A 2 (

—

3 • c • cr • p

5 ^р CM J

V tgP

A f Рдет , 7

где p д_ет — плотность материала детали.

Методика расчета удаления металла. Общее количество взаимодействий на площади квадрата упаковки (в случае упаковки абразивных частиц на поверхности детали по квадрату со стороной, равной диаметру описанной окружности), приводящих к микрорезанию, можно определить следующим образом:

n„ = PPt ,                                    ⁽²⁵⁾

p 12

где P 1 – геометрическая вероятность события, заключающегося в том, что любая точка квадрата упаковки покрывается пятном контакта за единицу времени воздействия массы абразивных частиц; P 2 – вероятность события, заключающегося в том, что взаимодействие абразивной частицы с поверхностью детали приведет к микрорезанию; t – время обработки.

В обычном случае, когда площадь поверхности детали больше квадрата упаковки, общее число взаимодействий, приводящих к микрорезанию,

^S дет ,                                         (26)

N р np S кв . уп .

где S дет – площадь поверхности детали; S кв.уп. – площадь квадрата упаковки.

Приняв S_keyn = D ² = 4 R ² , получим:

N_d = РРЛ^ ет .                             (27)

р 1 2 4 R 2

Разрушение поверхностного слоя при обработке свободными абразивами происходит преимущественно путем микрорезания. Следовательно, при расчете съема металла достаточно учитывать только число взаимодействий N p , приводящих к микрорезанию:

Q = Npq, где Q – съем металла с поверхности детали.

Подставив значение N p из (27), получим

S

Q = P i ? 2 tq 4R 2.                            (28)

Логично предположить, что появление случайных точек взаимодействия на поверхности детали подчиняется закону Пуассона. Предположим, что P 1 – это вероятность события, заключающаяся в том, что каждая точка квадрата упаковки покрывается пятном контакта в единицу времени.

Появление пятен контакта на детали подчиняется закону Пуассона. При этом вероятность появления k событий за время t определяется по формуле

₌ ( k t ) k e~^k                                               (29)

P(k)         k!     ’ где λ – интенсивность потока, т.е. среднее число взаимодействий в единицу времени на площади квадрата упаковки.

Соответственно зависимость для определения объема металла примет вид:

Q = Pλtq ^дет .                                   (30)

• ²    4 R ²

Величина λ зависит от технологических параметров (давление воздуха, зернистость абразива) и может быть определена при экспериментальном моделировании.

Заключение. Полученные зависимости позволяют прогнозировать удаление металла с поверхности детали при обработке свободными абразивами в зависимости от исходных технологических факторов. Эти зависимости могут быть положены в основу разработки методики определения времени обработки, необходимого для решения технологических задач.